让学生多维度思考问题

郁晶晶

在学完比的应用后，学生学习的劲头很足，对于一般的按比例分配的题目，做题的兴致很高，解答正确率高。如果遇上稍难的题目，学生会不会运用所学的知识顺利解答呢？为了培养学生灵活运用知识解决实际问题的能力，在整理与复习课上，我给学生出示了一道综合应用题：甲、乙两箱中粉笔盒数之比是5∶1，如果从甲箱里取出12盒放入乙箱中，甲、乙两箱中粉笔盒数的比变为7∶5，那么甲、乙两箱中共有粉笔多少盒？

这道题有一定的难度，我先让学生独立思考，然后一起探讨如何解题。在思考的过程中，很多平时一拿到题目就动笔写的学生轻蹙眉头，不知从何处下手；还有的学生不停地在草稿纸上写写、画画。10分钟后，有学生终于展颜，有了答案。于是我让解出答案的学生上台汇报。

这一方法是借助于按比例分配的思路，根据题意列出方程解题，解题的思路清晰，计算相对容易，其他学生容易理解。

生1的方法刚讲完，生2就迫不及待地汇报了他的方法，他是用比来解的。

生2的方法是：因为变化前甲、乙两箱中粉笔的盒数比是5∶1，那可以设乙箱原有粉笔x盒，则甲箱粉笔为5x盒，根据“甲箱里取出12盒放入乙箱后，甲、乙两箱中粉笔盒数的比变为7∶5”这一关键句来列方程。等量关系式为：（甲箱原有的粉笔盒数-12）∶（乙箱原有的粉笔盒数+12）=7∶5，列出方程为（5x-12）∶（x+12）=7∶5。

面对这一方程，学生们一筹莫展，都不会计算。于是我引导学生回顾所学的知识：“两个数的比就是什么？”生答：“两个数的比就是两个数相除。”学生茅塞顿开，反应快的马上把算式写成了（5x-12）÷（x+12）=7÷5，解出x=8，则5x=5×8=40，40+8=48（盒）。所以甲、乙两箱中共有粉笔48盒。

还有学生指出可以运用比例的基本性质“两内项之积等于两外项之积”来解：（5x-12）∶（x+12）=7∶5，则有（x+12）×7=（5x-12）×5，两边分别运用乘法分配律去掉括号，得到7x+84=25x-60，再根据等式的性质求出x=8。

这一方法所列方程计算时有点复杂，但是学生能够在老师的启发下根据比与除法的联系、比例的基本性质和等式的性质进行解答，也非常不错。

当我把期待和赞许的目光投向全班学生时，精彩又来了———

当学生沉浸在会心一悟时，我又要求学生对照板书，找出几种方法的异同，沟通方法之间的联系。学生积极交流、思辨，课堂呈现出从未有过的活跃。

一道综合题，学生居然得出了多种解法，我在惊叹之余，颇有感触。

综合题对相当一部分学生来说是有挑战性的。教师要先给学生尝试的机会，让他们有独立思考的时间。对很多学生来说，只有思维碰壁后，才会有想要学习、想要掌握、想要傾听的意愿。

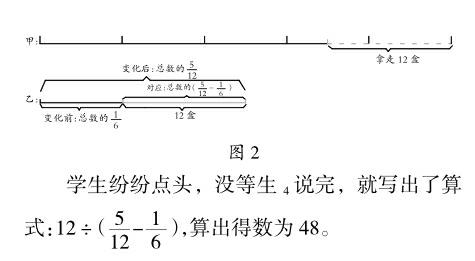
在解决这道综合题的过程中，正是由于教师给足了学生思考的时间，学生得出了不同的解题方法。教师及时引导学生进行对比、辨析，沟通了这些方法之间的内在联系，使训练效果达到最大化。尤其值得一提的是，方法三采用了量率对应的方法解决问题。运用这一方法把比的应用问题转化成分数乘除法应用题，实现比与分数之间的快速转化是前提，理清量率之间的对应关系是关键，利用线段图帮助理解题意是一种重要策略。从案例中我们可以发现，学生理解方法三是有困难的，而借助线段图，较好地实现了比与分数之间的转化、量率对应关系的建立和基本数量关系的表达。由于受到方法三的思路的启发，有学生甚至自然迁移出另一种方法。

数学是锻炼思维的体操，是启迪智慧的钥匙。培养学生的数学思维是数学教学的基本任务之一。在教学中，教师要让学生多维度思考问题，鼓励学生进行探讨，把思考引向深入。本节课虽然教学时间延长了20分钟，但学生的思维是活跃的。他们在不断探索的过程中找到了方法，收获了自信，极大地增强了成功感，解题能力也得到了提高。

（作者单位：江苏省海门市海南小学）