巧妙变式 培养解题能力

于真灵

解题教学中，要让学生跳出题海，运用所学的知识和方法应对千变万化的试题，教师应结合教材精选题目，巧妙进行变式，充分发挥典型试题的带动作用和举一反三的功能，让学生悟通练透。

一、变更教材中题目的数据（符号），帮助学生巩固知识

例1（人教A版·选修2-1，P69例4）斜率为1的直线l经过抛物线y2=4x的焦点F，且与抛物线相交于A，B两点，求线段AB的长。

点评：对教材中题目的条件进行变换，能够帮助学生迁移知识，培养迁移能力。

三、变换教材中题目的背景，促使学生活用知识

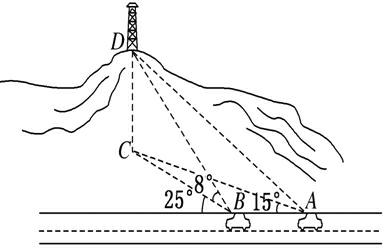
例3（人教A版·必修5，P14例5）如右图，一辆汽车在一条水平的公路上向正西行驶，到A处时测得公路北侧远处一山顶D在西偏北15毅的方向上，行驶5km后到达B处，测得此山顶在西偏北25毅的方向上，仰角为8毅，求此山的高度CD（精确到1m）。

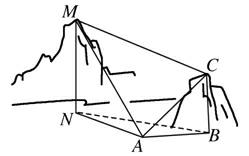
变式：如右图，为测量山高MN，选择A和另一座山的山顶C为测量观测点。从A点测得M点的仰角蚁MAN=60毅，C点的仰角蚁CAB=45毅以及∠MAC=75毅；从C点测得∠MCA=60毅，已知山高BC=100m，則山高MN=________m。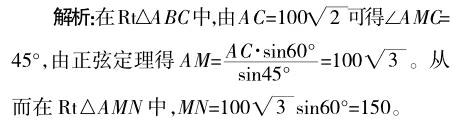

点评：变换教材中题目的背景，让题目披上新妆，促使学生活用所学的知识解题，能够培养学生的应变能力。

四、应用教材中题目的结论，帮助学生拓展知识

例4（人教A版·必修1，P39B组第3题）已知函数f（x）是偶函数，而且在（0，+∞）上是减函数，判断f（x）在（-∞，0）上是增函数还是减函数，并证明你的判断。

变式：已知偶函数f（x）在[0，+∞）单调递减，f（2）=0。若f（x-1）>0，则x的取值范围是________。

解析：由已知得f（|x|）在[0，+∞）单调递减，f（2）=0，从而f（x-1）>0可化为f（|x-1|）>f（2），从而|x-1|<2，所以-1

点评：教师在学生平时学习时，注意引导他们记忆教材题目中的一些重要方法和结论，积累解题经验，切实提高解题能力。

五、一题多变，引导学生追根溯源

点评：本题主要是掌握利用基本不等式求最值的方法及注意点。

教材中的例题、习题是经过精心挑选而设计的，它蕴藏着丰富的思想方法和研究资源。而不少试题所涉及的思想方法都源于教材。教学中，教师要引导学生做到对教材中的经典题目能够熟练地求解，掌握它的通性通法、思路分析及知识内涵。这就要求教师要深入研读教材、汲取营养，充分发挥例题、习题潜在的功能，发挥教材母本的作用，在此基础上进行变式教学，通过多题一解培养学生的求同思维，通过一题多解培养学生的求异思维，通过一题多变培养学生思维的灵活性与深刻性。

（作者单位：绥宁县第一中学）