某高转速相控阵雷达抗风能力分析*
2017-08-29刘建军沈文军
刘建军,沈文军
(南京电子技术研究所, 江苏 南京 210039)
某高转速相控阵雷达抗风能力分析*
刘建军,沈文军
(南京电子技术研究所, 江苏 南京 210039)
文中论述了引起高转速雷达车倾覆和滑移的各种外力因素,并给出了具体的计算公式。以某高转速相控阵雷达为例,分析了高转速产生的惯性力(矩)占总倾覆力(矩)的比例,并对高风载工况下的抗倾覆能力和抗滑移能力进行了分析和计算。结果表明,雷达车满足抗倾覆、抗滑移的要求。
高转速;相控阵雷达;抗倾覆和抗滑移能力
引 言
现代科学技术的迅猛发展,日益需要现代军用雷达能提供更短的反应时间以对付高速喷气飞机、制导导弹、弹道导弹和人造卫星。同时反恐、维和、突发事件应对等小范围战场往往面临来自各个方向、多种威胁目标的攻击,雷达全向化、高目标探测需要更高的数据率,而提高天线转速是提高数据率的一个重要手段。但天线方位转速的增加会相应增加雷达转动部分的惯性力和力矩,尤其是天线质量相对较大的相控阵雷达,对雷达的抗倾覆能力提出了更高的要求。一些学者研究了天线转速对雷达结构设计的影响,提出了高转速雷达的结构设计要点[1],对雷达天线结构进行了简化并建立了有限元模型,分析了关键风速下的应力应变,验证了天线设计的可靠性[2]。
本文分析了雷达在高转速下引起雷达车倾覆的各种外力因素,对阵面因旋转产生的附加力矩进行了理论公式推导,计算分析了某相控阵雷达车在高转速、高风载条件下的抗倾覆、抗滑移能力。
1 雷达倾覆力分析
1.1 某相控阵雷达结构
该雷达设备集成于一辆单车上,天线阵面和天线座转台均为箱体结构,有较大的质量及转动惯量。天线阵面和天线座转台作360°无限制转动,最大转动角速度达30 r/min。雷达作方位转动时由4条抗倾覆腿(调平腿)支撑,雷达车的工作状态如图1所示。
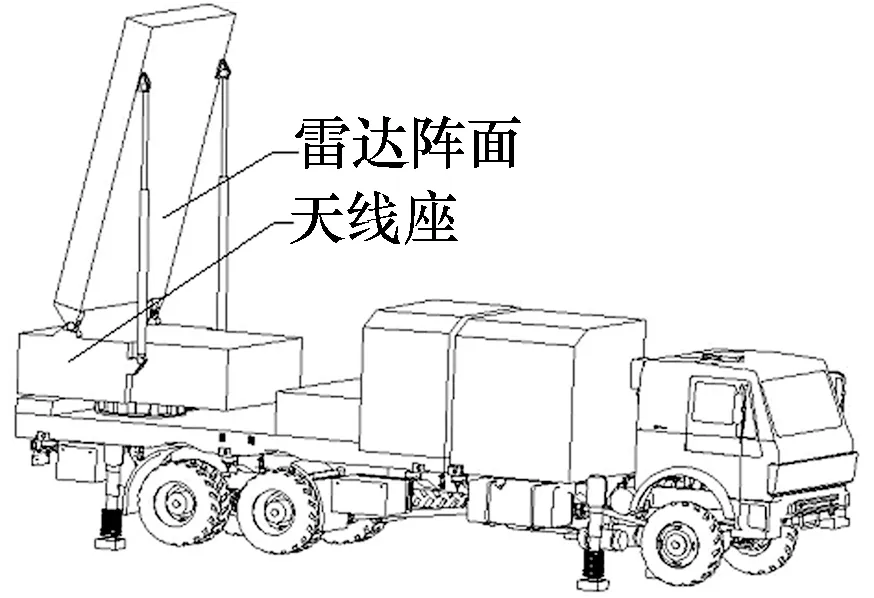
图1 某雷达车工作状态
1.2 引起雷达车倾覆的因素
如图2所示,雷达抗风能力分为克服雷达车所受侧向力的抗滑移能力和克服所受倾覆力矩的抗倾覆能力[3]。雷达阵面在高速旋转时,受到的侧向力Fx包括侧向风力F1和偏心转动设备的惯性力F2;倾覆力矩M倾包括风力矩M1、惯性力矩M2和阵面倾斜引起的附加力矩M3。
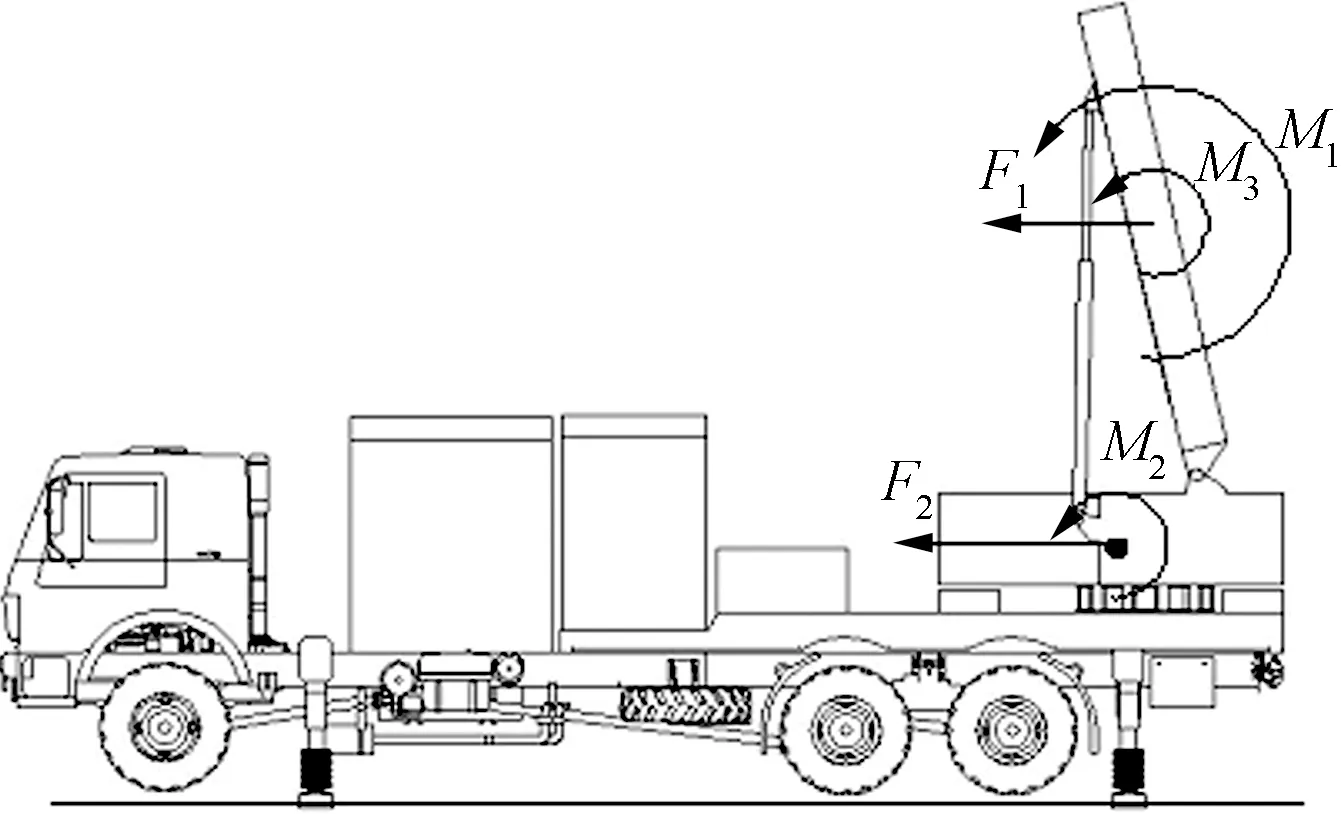
图2 雷达车倾覆力、力矩示意图
1.3 雷达车风力F1、风力矩M1分析
计算风力时,将整车分为阵面、平台设备、操控舱和载车4个部分,各部分的风力F1和风力矩M1按下式计算[4]:
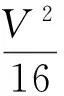
(1)
式中:C为风阻力系数,取1.4;A为物体特征面积,m2;V为风速,m/s。
M1=F1H
(2)
式中,H为风力中心距地面的高度,m。
阵面的前后部迎风面积最大,而载车、平台等不回转部分的侧向迎风面最大。当阵面转至载车侧面时,整车所受风力最大,同时因抗倾覆腿(调平腿)侧向间距最小,抗倾覆能力最差,因此整车侧向最容易倾覆。计算风力时按侧向工况计算,将各个部分的物体特征面积A代入式(1)计算得[2]:
F1=F1,阵面+F1,平台+F1,操控舱+F1,载车=
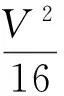
将各个部分的物体特征面积A和风力中心距地面的高度H代入式(2)计算得:
M1=M1,阵面+M1,平台+M1,操控舱+M1,载车=
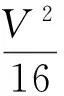
A载车H载车)=81V2
1.4 惯性力F2、惯性力矩M2分析
转动设备偏心,在转动时会产生侧向惯性力F2:
F2=m偏ω2R
(3)
式中:m偏为偏心设备质量,kg;ω为阵面角速度,rad/s;R为偏心距,m。
惯性力矩M2为:
M2=F2H2=m偏RH2ω2
(4)
式中,H2为偏心设备质心距地面的高度,m。
图3为雷达车的惯性力和惯性力矩示意图。
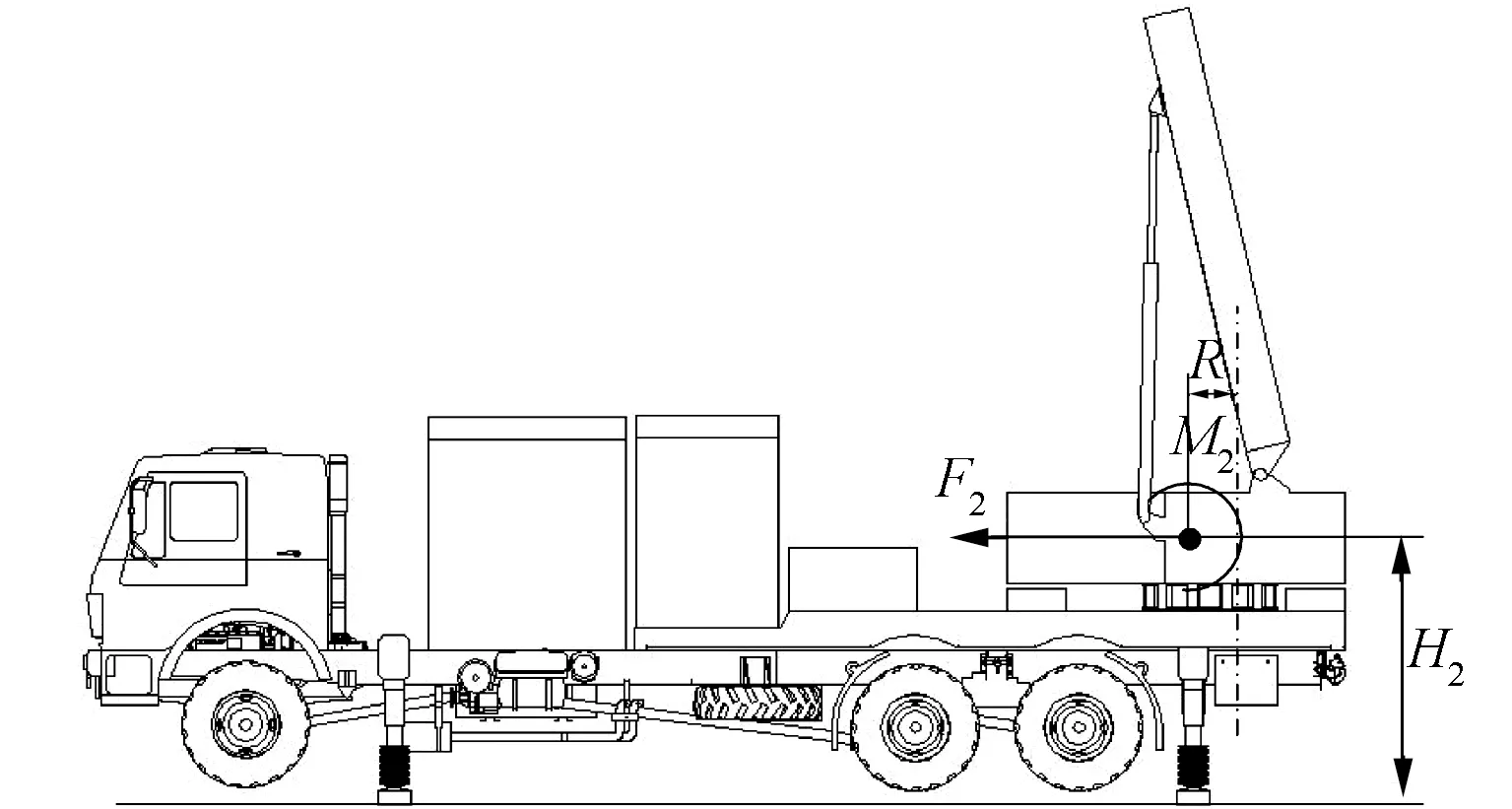
图3 雷达车惯性力和惯性力矩示意图
将阵面及转台的相关参数代入式(3)、式(4)得:
F2=F2,阵面+F2,转台=ω2(m阵面R阵面+m转台R转台)=
2 600R阵面ω2+3 600R转台ω2
M2=M2,阵面+M2,转台=ω2(m阵面R阵面H2,阵面+
m转台R转台H2,转台)=13 000R阵面ω2+
8 640R转台ω2
式中:m阵面和m转台分别为阵面和转台的质量;R转台和R阵面分别为转台和阵面的偏心距。
从式(3)和式(4)可以看出:偏心力(距)与偏心距及方位转动角速度的平方成正比,因角速度为指标要求,所以偏心力(距)与偏心距成正比,如图4和图5所示。在结构设计时,应合理布局,尽量减小偏心距,必要时增加配重[1]。
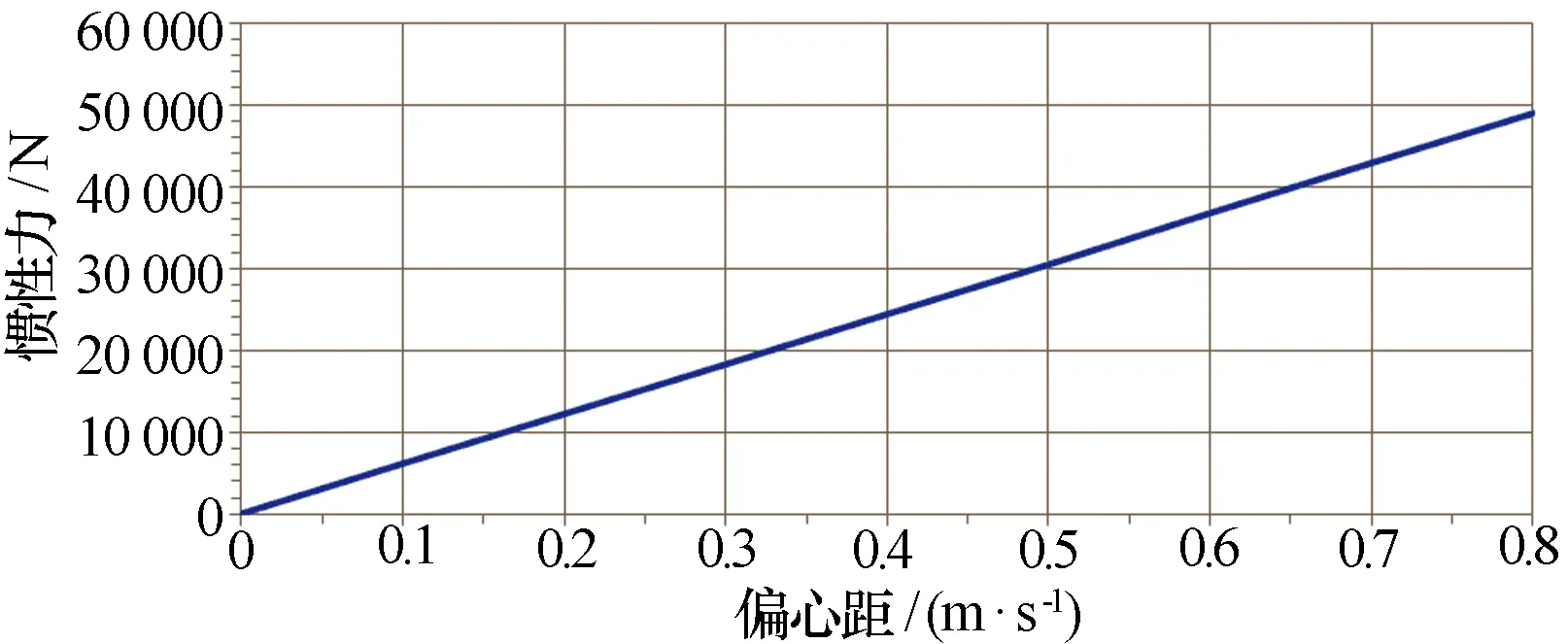
图4 雷达车不同偏心距下的惯性力
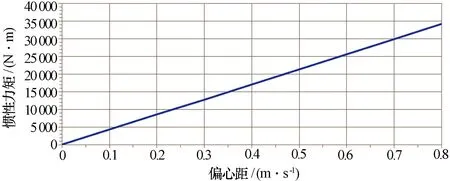
图5 雷达车不同偏心距下的惯性力矩
考虑到实际与理论设计会存在一定的偏差,如采用配重的方式调整重心的位置会增加整车的重量,因此设计时允许一定的偏心,计算时偏心距R按0.2 m考虑,则:
F2= 2 600R阵面ω2+ 3 600R转台ω2= 1 240ω2
M2= 13 000R阵面ω2+ 8 640R转台ω2= 4 328ω2
1.5 阵面倾斜引起的附加力矩M3
倾斜安装的阵面旋转时,每个质点会产生惯性力Fi。如图6所示,取阵面几何中心为原点O,建立三维直角坐标系O-XYZ,则质点(Xi,Yi,Zi)的惯性力可分解为阵面前向Fi,x和阵面侧向Fi,z2个分力[5]:
Fi,x=miω2ri,x=miω2xi
Fi,z=miω2ri,z=miω2zi
式中:mi为质点的质量;ri,x和ri,z分别为质点在X轴和Z轴方向的回转半径。
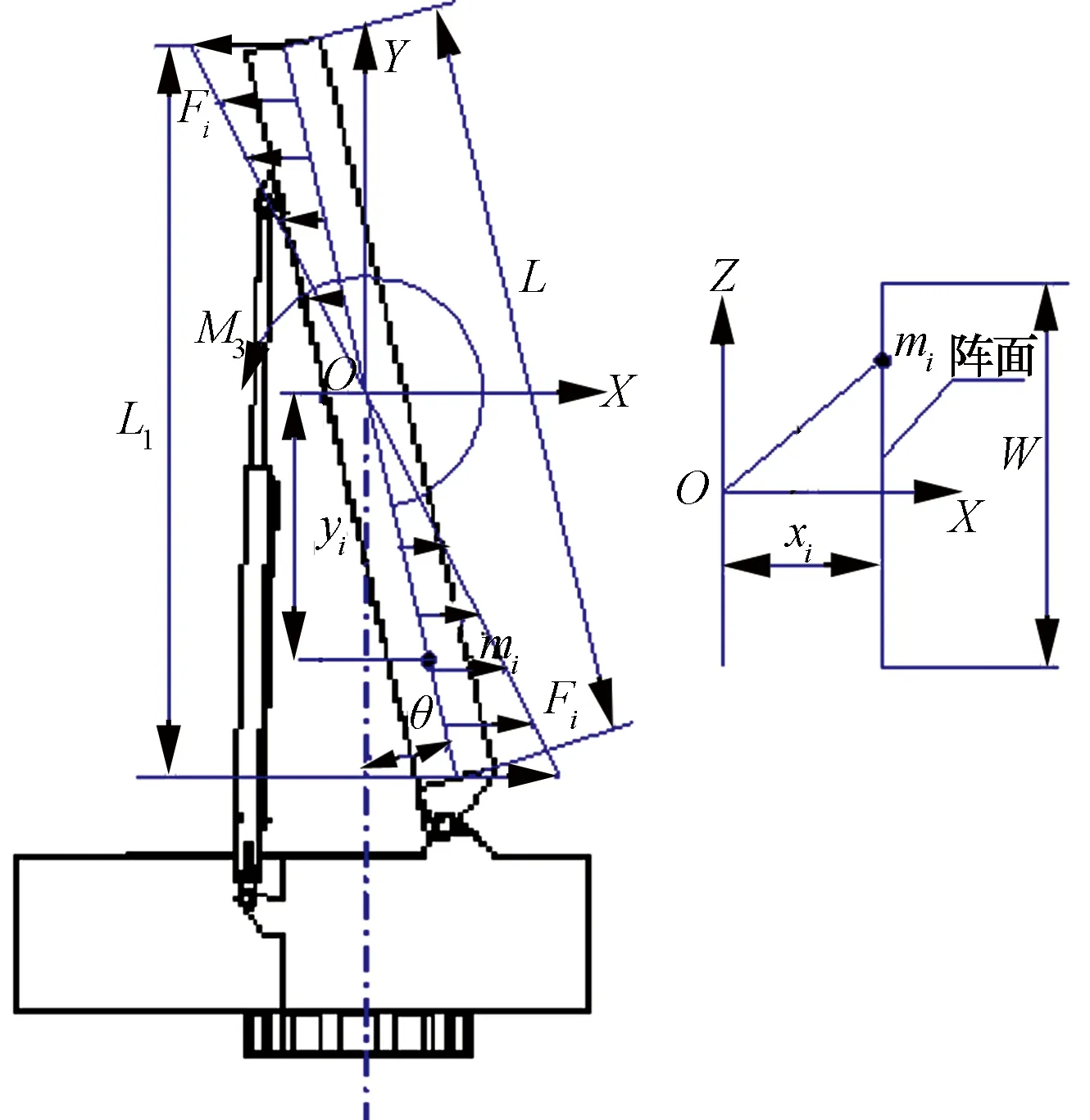
图6 阵面各质点惯性力示意图
由质点(Xi,Yi,Zi)的惯性力Fi产生的相对阵面中心的力矩为:
Mi,x=Fi,xyi=miω2xiyi=ω2tan(θ)miy2i
Mi,z=Fi,zyi=miω2ziyi
式中,θ为阵面倾角。
阵面由X轴方向惯性力产生的相对阵面中心的总力矩为:
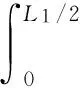
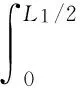
m阵面ω2tan(θ)L2cos3(θ)/12=
m阵面ω2L2sin(θ)cos3(θ)/12
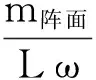
阵面由Z轴方向惯性力产生的相对阵面中心的总力矩为:
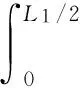
因阵面左右相对回转轴对称,质点阵面侧向的分力可与对称位置质点的侧向分力相互抵消,因此Mz= 0。
因此,旋转产生的惯性力形成的倾覆力矩为:
M3=Mx=m阵面ω2L2sin(θ)cos(θ)/12
(5)
式中:ω最大为30r/min;θ=13°;L= 4m。
将各参数代入式(5)得:
M3=m阵面ω2L2sin(θ)cos2(θ)/12=740ω2
1.6 雷达车所受的侧向力Fx
雷达所受到的侧向力Fx为侧向风力F1和偏心转动设备的惯性力F2的总和,即:
Fx=F1+F2= 34V2+1 240ω2
(6)
当转速为30r/min、最大风速为25m/s时,由风引起的侧向力为21 125N,占总侧向力的63.3%;由转动惯性力引起的侧向力为12 238N,占总侧向力的36.7%,表明高转速雷达更可能产生雷达车滑移。
1.7 雷达车倾覆力矩M倾
雷达倾覆力矩M倾为风力矩M1、惯性力矩M2和阵面倾斜引起的附加力矩M3的总和,即:
M倾=M1+M2+M3= 81V2 + 4 328ω2+740ω2=
81V2 +5 068ω2
当转速为30r/min、最大风速为25m/s时,由风引起的倾覆力矩M1为50 625 N·m,由转动引起的倾覆力矩M2+M3为50 019 N·m,占总倾覆力矩的49.7%。除风力矩外,高转速引起的惯性力矩也是造成雷达车倾覆的一个重要因素。
2 雷达车抗风能力分析
2.1 抗滑移能力分析
雷达车侧向稳定力为:
F稳=mgμ
式中:m为雷达车整车质量,m= 27 705 kg;g为重力加速度;μ为摩擦系数,取μ= 0.35。
则抗滑移安全系数为:
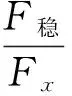
当ω= 30 r/min时,不同风速下抗滑移安全系数如图7所示。当风速为25 m/s时,nc= 1.77,雷达车不会产生侧向滑动。
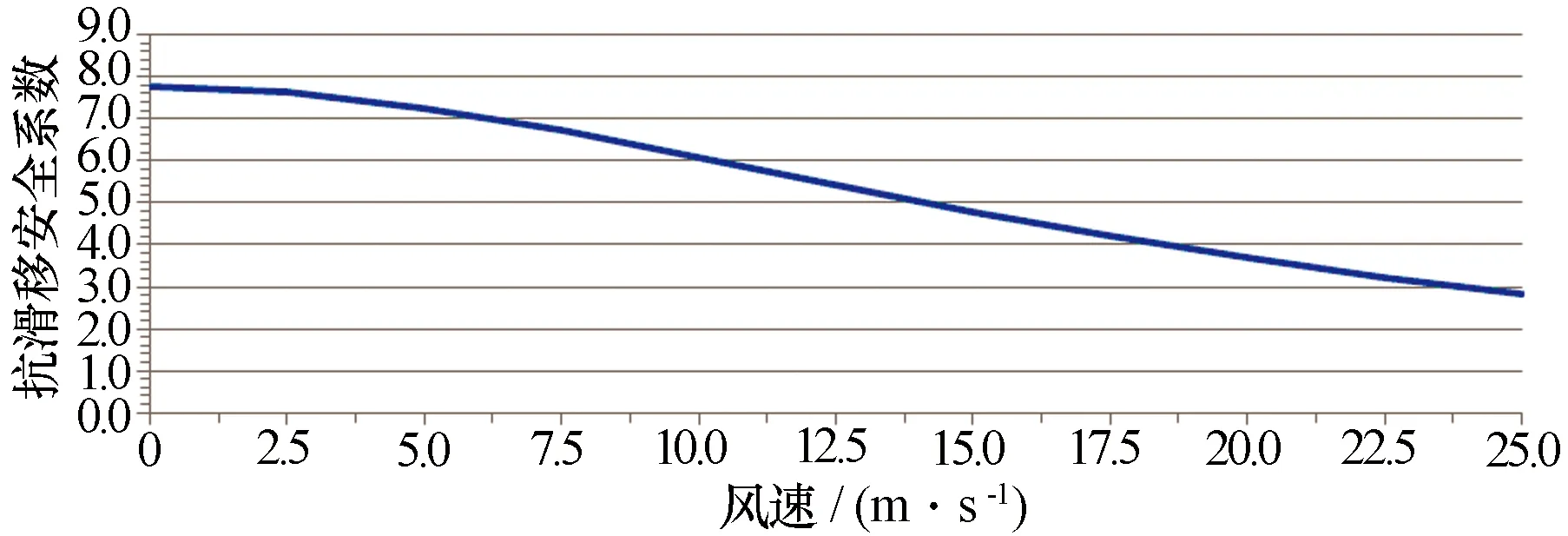
图7 雷达车抗滑移安全系数
2.2 抗倾覆能力分析
雷达车稳定力矩为:
M稳=mgR
式中:雷达车整车质量m=27 705 kg; 最小抗倾覆半径R= 1.03 m。
则抗倾覆安全系数为:

当ω= 30 r/min时,不同风速下抗倾覆安全系数如图8所示。当风速为25 m/s时,Nc= 2.8,雷达车不会倾覆。
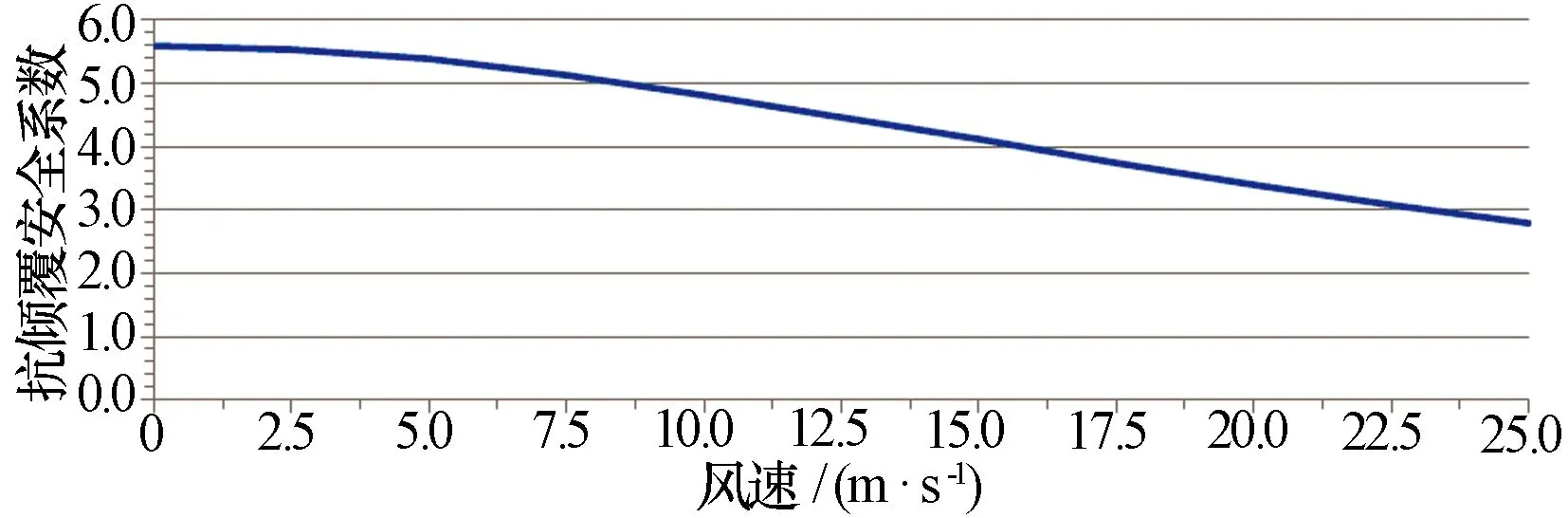
图8 雷达车抗倾覆安全系数
3 提高整车抗风能力的设计要点
从分析计算可以看出:雷达车产生滑移的因素有侧向风力和惯性力;雷达车产生倾覆的因素有风力矩、惯性力矩和阵面倾斜引起的附加力矩。在设计过程中应尽量减小回转部分的偏心距,降低设备的重心,设计合适的倾覆腿间距。
4 抗风试验情况
该雷达在最大风速25 m/s时,以30 r/min的转速高速转动,未出现侧向滑移、调平腿离地现象。对整车进行应力测试,最大应力为185 MPa,小于该处材料Q345的屈服强度,满足强度要求。试验表明,该雷达在高转速、高风速条件下工作是稳定安全的。
5 结束语
本文根据高转速引起雷达倾覆和滑移的各种外力进行了分析,对某高转速相控阵雷达抗倾覆、抗滑移能力进行了分析计算。结果表明:该雷达在高转速和高风速工况下具备抗倾覆和抗滑移的能力;同时,由高速转动产生的惯性力(矩)与最大工作风速产生的风力(矩)相关。在结构设计时,应严格控制各旋转设备重心的位置。文中的计算方法,特别是推导的阵面旋转时产生的附加力矩的计算公式可为类似产品的分析计算提供参考。
[1] 赵新舟. 提高天线转速对某雷达结构设计的影响[C]//2006年全国电子机械和微波结构工艺学术会议论文集. 南京: 中国电子学会电子机械工程分会, 2006.
[2] 侯学兵, 高锋华. 某雷达天线的风载荷分析[J]. 电子机械工程, 2010, 26(3): 40-42.
[3] 赵德昌. 地面高机动雷达结构总体设计探讨[J]. 电子机械工程, 2007, 23(3): 19-23.
[4] 沈文军. 大型天线舱风载作用下力学特性及稳定性分析[J]. 机械设计与研究, 2010(3): 108-111.
[5] 哈尔滨工业大学理论力学教研室.理论力学(上、下) [M]. 北京: 高等教育出版社, 1981.
刘建军(1976-),男,硕士,高级工程师,主要从事雷达结构总体设计工作。
Anti-overturn Stability Analysis of a Phased Array Radar with High Rotation Speed
LIU Jian-jun,SHEN Wen-jun
(NanjingResearchInstituteofElectronicsTechnology,Nanjing210039,China)
In this paper, different types of external forces that cause overturning and slipping of the radar vehicles with high rotation speed are analyzed and the formulas are deduced. Taking a phased array radar as an example, its anti-overturn and anti-slip stability under high rotation speed and large wind load is analyzed and calculated. The results show that the anti-overturn and anti-slip stability of the phased array radar meets the design requirement.
high rotation speed; phased array radar; anti-overturn and anti-slip stability
2016-11-20
TN956
A
1008-5300(2017)02-0037-04
