基于蚁群算法的复合材料结构件的返修计划问题*

姚智骞

(东南大学机械工程学院， 江苏 南京 211189)

基于蚁群算法的复合材料结构件的返修计划问题*

姚智骞

(东南大学机械工程学院， 江苏 南京 211189)

为解决目前生产中出现的复合材料结构件的质量缺陷问题，G公司设立了复合材料结构件返修工序。针对结构件返修计划问题，以最大化返修计划中的结构件数量为目标，同时兼顾公司出货计划延迟和WIP成本(在制品成本)增加的情况，建立了0-1整数规划模型，进而以蚁群算法为基础提出了2种伪随机选择规则。根据实际情况采用不同参数设计算例来验证算法的性能。结果表明在最大化返修结构件数量方面，算法一优于算法二，而在减小公司出货延迟和控制WIP成本方面，算法二优于算法一。

返修计划; 整数规划; 蚁群算法; 伪随机选择机制

引 言

G公司是一家专业生产、组装、测试各类航空用零部件、组装部件、系统的制造企业，其中A型飞机机翼复合材料结构件(以下简称结构件)是该公司刚刚推出的主要产品。G公司生产的结构件采用碳纤维蜂窝夹层结构，如图1所示，这种结构是一种特殊的复合材料(由2种或2种以上不同性质的材料，通过物理或化学的方法，在宏观或微观上组成具有新性能的材料)，即在2块强度和弹性模量较大的面层材料中间(称作面板或蒙皮)夹着厚而轻的蜂窝芯材，并采用胶粘剂(热固性树脂)在一定温度和压力下复合成一个整体刚性结构。其中蜂窝由凯夫拉纤维浸渍上树脂，通过胶接拉伸法或波纹压形胶接法制得[1]，面层材料采用的是碳纤维预浸料(把树脂浸渍在碳纤维中制成片状的叠层材料)[2]。结构件90%由碳纤维、树脂和蜂窝组成，其余10%由玻璃纤维、胶膜和油漆组成。因为生产工艺存在缺陷，G公司每个月生产的结构件中20%存在轻微质量缺陷。经过工艺工程师和质量工程师的仔细检查，查明引发缺陷的原因是在固化过程[3](碳纤维和蜂窝在一定温度和压力下复合的过程)中装配区液态粘合树脂流入蜂窝夹层[4]，从而导致装配区域厚度低于公差下限0.1～0.5 mm左右。虽然力学试验和超声波无损检验结果表明，流入蜂窝的粘合树脂对结构件的力学性能和质量没有显著影响，但未达标的装配区域厚度会导致装配在结构件上的金属件和胶皮无法紧密连接在结构件上，造成质量隐患。经过工程师和设计部门的反复沟通，确认在现有工艺技术条件下粘合树脂流入蜂窝是不可避免的情况，但是可以在不影响结构件其他性能的前提下通过返修的方式来增加相关装配区域的厚度。

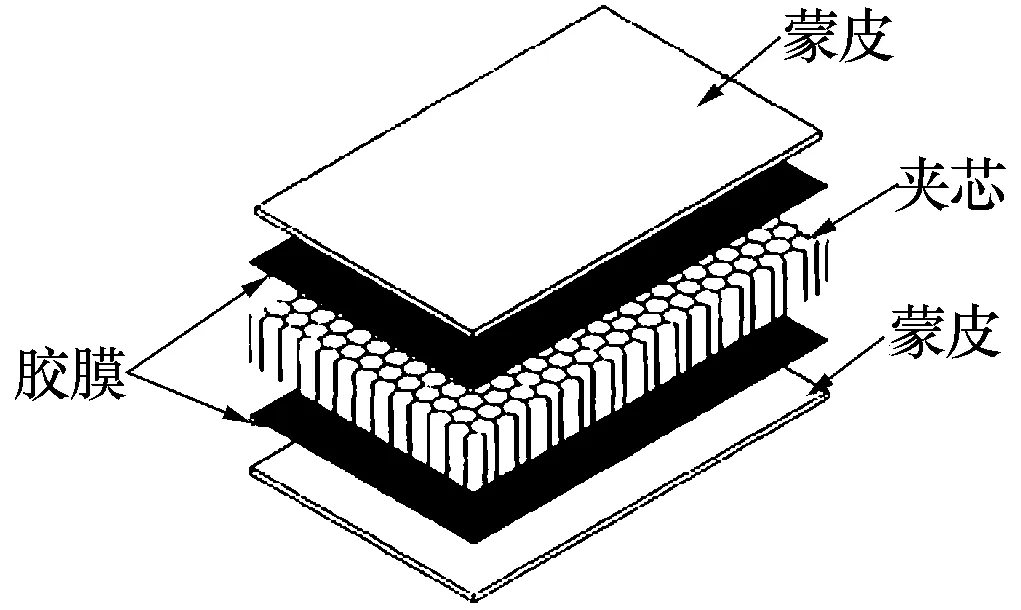
图1 碳纤维蜂窝夹层结构

G公司目前积攒了200多件有质量缺陷的结构件，同时随着生产的进行，数量还在不断增加。大量积压的结构件次品意味着公司需要付出不菲的交货计划推迟(违约)成本，同时公司的WIP成本(在制品成本)也随之不断增加。另外，结构件次品需要占用大量的存储空间，如不及时妥善处理和保管可能会影响正常生产，也可能造成这些次品受损甚至报废。因此，为尽快完成积压结构件次品的返修任务，需要制订科学合理的返修生产计划。本文研究重点是结构件次品的返修生产计划问题，首先对该问题进行了详细描述，接着给出了该问题的数学模型，然后设计了2个蚁群算法来求解该问题，并采用算例验证所提算法的性能。

1 问题定义和数学模型

结构件次品的返修生产计划问题可以概括为：已知共有n个结构件次品和m个返修时段，寻找一个最优返修生产计划，使得在所有返修时段内安排的结构件数量最大。

问题假设如下：

1)结构件的一次返修成功率为100%，这样无需为同一结构件次品安排二次返修。

2)结构件一个返修区域的返修时间固定为t0，因此每个结构件的返修时间与其返修区域的数量成正比。

表1 参数和变量

对于返修计划建立如下模型：

(1)

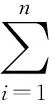
(2)

Ej≥Ej+1j=1,2,…,m-1

(3)

式(1)为目标函数，表示在m个返修时段内，最大化返修结构件的数量。式(2)表示在第j个返修时段内，所有计划返修结构件的预计返修时间总和不能超过一个返修时段的时长T。式(3)表示第j个返修时段的返修紧急程度指数应大于第j+1个返修时段的返修紧急程度指数。

出货延迟程度指数pi是按照结构件i的出货延迟日期来确定的延迟等级，分为3个等级，分别是正常出货(0.1)，延迟出货3个月以内(0.3)，延迟出货3个月以上(0.6)，每个等级的出货延迟程度指数是根据对应等级结构件次品在结构件次品总体中的比例确定的。ci是结构件i在所有待返修结构件中的相对WIP成本，由式(4)计算而得：

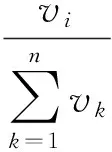
(4)

返修紧急程度指数ki是由结构件i的出货延迟程度指数pi和相对WIP成本ci加权平均得到的新指标，体现了结构件的返修综合紧急程度，pi和ci的权重分别为w1和w2，ki由式(5)计算而得：

ki=w1pi+w2cii=1,2,…,n

(5)

返修紧急程度指数Ej是第j个时段内所有结构件返修紧急程度ki的总和，表示第j个返修时段的返修紧急程度指数，由式(6)计算而得：

(6)

2 蚁群优化算法

蚁群优化算法(AntColonyOptimization，ACO)，是一种用来寻找优化路径的概率型算法。它由意大利学者MarcoDorigo等[5-6]于1991年提出，其灵感源于蚂蚁在寻找食物过程中发现路径的行为。蚁群算法是一种模拟进化算法，初步研究表明该算法具有许多优良的性质。Dorigo等[7]在1997年又提出了一种具有全新机制的ACO算法——蚁群系统(AntColonySystem)，进一步提高了ACO的性能。新蚁群算法的不同之处主要体现在3个方面：1)使用一种伪随机比例机制选择下一个节点，以寻求开发当前路径与探索新路径之间的平衡；2)信息素全局更新过程中只在属于至今最优路径的边上释放信息素；3)新增信息素局部更新过程，即蚂蚁每次经过空间内的某条边时都会除去边上一定量的信息素，以增加后续蚂蚁探索其余路径的可能性。

本章结构件的返修生产计划问题是一个NP-hard问题，这意味着当问题规模较大时，很难在可接受时间范围内求得精确解。因此，结合所研究的返修计划问题，提出了一个蚁群优化算法，以在较短时间内求得较优的近似解。蚁群算法所涉及的参数符号及说明如表2所示。

表2 蚁群算法参数说明

蚁群算法的基本思路是：首先对信息素矩阵进行初始化，然后通过多次迭代寻找最优解。在每次迭代中，首先让每只蚂蚁随机选择第一个结构件，然后按照状态转移规则选择后续结构件，并且每当一只蚂蚁k选择一个结构件i后，马上进行信息素的局部更新。当所有蚂蚁都构建完自己的返修计划后，选出本次迭代的最优返修计划Plan+，然后与存储的至今最优返修计划Planmax比较，若Plan+优于Planmax，则用Plan+替代Planmax，反之则保持Planmax不变，然后进行信息素的全局更新，最后重复迭代操作直至最大迭代次数tmax。在蚁群搜索结束后，根据式(3)对最优返修计划Planmax按照返修紧急程度指数Ej从大到小排序。蚁群算法的关键在于信息素设置、返修计划构建方法、返修计划评估以及信息素的更新，下面分别介绍这几个关键环节。

2.1 信息素设置

信息素定义在任意一对结构件i和j之间，表示在结构件i后选择结构件j的倾向程度，对应的信息素浓度为τij。设立一个n×n信息素矩阵，存储所有信息素信息。初始化信息素矩阵时，将信息素矩阵中的值赋为一个较小的正值τ0。

2.2 构建返修计划

返修计划构建采用串行方式进行，即在一次迭代过程中，每只蚂蚁依次构建一个完整的返修计划，这样每次迭代共产生ants个返修计划。首先蚂蚁k随机选择第一个结构件i，然后蚂蚁k根据状态转移规则确定下一个要选择的结构件j，选择的过程依赖信息素和启发式信息的共同作用，每只蚂蚁都按照这种方式选择结构件，直到所有蚂蚁都构建完成结构件返修计划。在第2.1节中已对信息素做了说明，下面将对启发式信息进行定义和使用。在选择结构件时，启发式信息将引导蚂蚁优先选择符合模型目标的结构件。定义在第t次迭代中在结构件i后选择结构件j的启发式信息为ηij(t)：

(7)

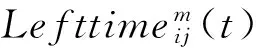
(8)

(9)

相比于机制一，机制二考虑了另外一个启发式信息，即考虑了结构件的返修紧急程度priorityj(t)，目的是优先安排更为紧急的待返修结构件。机制二如下：

(10)

(11)

在第t次迭代中蚂蚁k选择结构件j后，计算返修时段m已用时间，确保已用时间小于返修时段固定时长。

2.3 返修计划评估

返修计划优劣的评价指标为结构件总数numberk(t)。每次迭代完成后，比较每只蚂蚁所构建的返修计划优劣，得到本次迭代的最优返修计划Plan+，与存储的至今最优返修计划Planmax进行比较，若Plan+优于Planmax，则用Plan+替代Planmax，反之则保持Planmax不变。

2.4 信息素更新

2.4.1 信息素局部更新

为增加后续蚂蚁探索其他路径的可能性，在返修时段计划的构建中，对于每只蚂蚁，每当选择一个结构件j后(前一个结构件为i)，将立刻对结构件i和结构件j之间的信息素τij(t)进行局部更新。如式(12)所示：

τij(t)=(1-ρ1)τij(t)+ρ1τ0

(12)

式中，ρ1是一个[0, 1]区间内的参数。

2.4.2 信息素全局更新

在每次迭代后，按照优化目标对所有蚂蚁构建的返修时段计划进行评估，然后进行信息素的全局更新。在信息素全局更新时，只对至今最优返修时段计划进行信息素的释放。如式(13)和(14)所示：

τij(t+1)=(1-ρ2)τij(t)+ρ2Δτij(t)

(13)

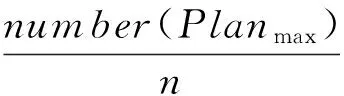
(14)

式中：ρ2是一个[0, 1]区间内的参数；number(Planmax)为搜索得到的至今最优返修计划序列的结构件总数。

蚁群算法执行流程如下：

3 算例验证与结果分析

3.1 算例设计

通过设计算例来验证文中所提蚁群算法的性能。算例设计所用参数根据G公司实际生产情况设定，如表3所示。

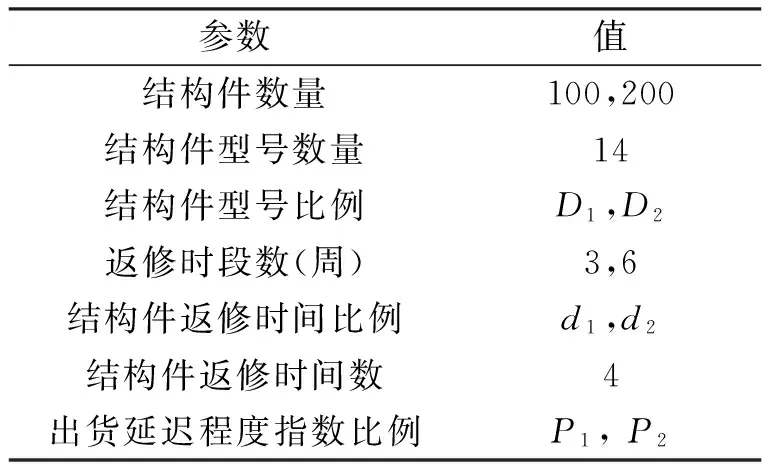
表3 算例参数

待返修结构件总数设为100或200个。G公司结构件共有14个型号。型号比例采用D1和D2两种，D1为平均比例，即每种型号的比例相同，表示在一段较短时间内，每种型号出现质量缺陷的比例相同；D2为累积比例，即每种型号的比例根据实际累积情况产生，表示在一段较长时间内，G公司累积了大量的质量缺陷结构件，不同型号之间的比例不尽相同。返修生产计划期包括3周和6周(每周为一个返修时段)两种，对应于100和200个待返修结构件。另外待返修结构件预计返修时间有4种，预计返修时间根据返修区域的数量确定。预计返修时间比例为d1和d2，d1为固定返修时间比例，表示通常情况下，每种型号的返修区域数量确定，所以返修时间也就随之确定。d2为累积返修时间比例，即根据实际累积结构件返修区域数量确定的返修时间比例，表示在一段较长时间内，经过累积，每种型号的返修区域数量不固定，因此返修时间也就随之变化。

结构件型号和返修时间比例如表4所示。在累积返修时间比例d2中，以PANEL10为例，40(75%) 80(25%)表示返修时间为40min的PANEL10占比75%，返修时间为80min的PANEL10占比25%，后面所有型号依此类推。

表4 型号和返修时间比例

出货延迟程度指数比例为P1和P2，如表5所示。P1为平均比例，即3个等级的出货延迟程度比例相同，如100件待返修结构件中，3个等级的结构件各占33.3%。P2为累积比例，即3个等级的出货延迟程度比例不同，具体比例由实际累积结构件中情况确定。同时P1和d1，P2和d2之间互相对应。其中P1和d1均为平均比例，表示在较短时间内返修时间和出货延迟程度的比例，而P2和d2均为累积比例，表示在较长时间内两个指标的比例。

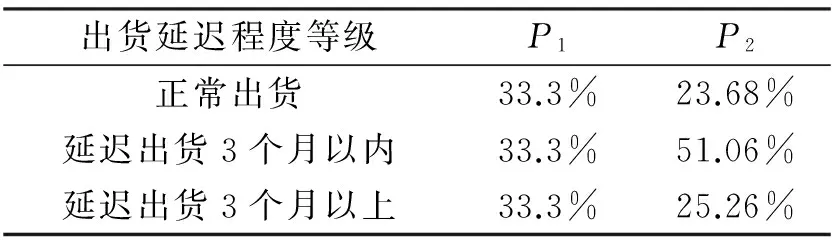
表5 出货延迟程度指数比例

根据以上参数通过C++程序随机产生算例，结构件数量、返修时间分布和出货延迟程度分布经排列组合产生8个算例，如表6所示。

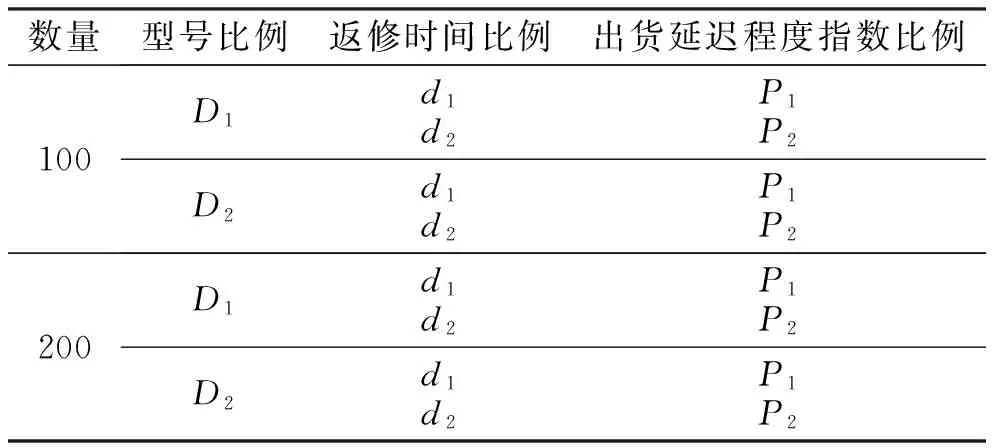
表6 算例组合

3.2 算法性能验证与分析

本文设计的两种算法均采用微软公司的VisualStudio2012C++编译，实验环境为IntelCorei5CPU@ 2.5GHz, 3GBRAM，Windows7系统。蚁群算法参数设置如下：

机制一：

ants = 10，tmax= 200，τ0= 0.005，ρ1= 0.01，ρ2= 0.01，α = 1，β = 3，q0= 0.9，w1= 10，w2= 100，T = 2 400min。

机制二：

ants = 10，tmax= 200，τ0= 0.005，ρ1= 0.01，ρ2= 0.01，α = 1，β = 3，ε = 3，w1= 10，w2= 100，q0= 0.9， T = 2 400min。

采用算法一和算法二基于以上参数设置运行算例，每个算例运行3次，取平均值作为该算例的运行值。两种算法的结果如表7、表8、图2～图6所示。

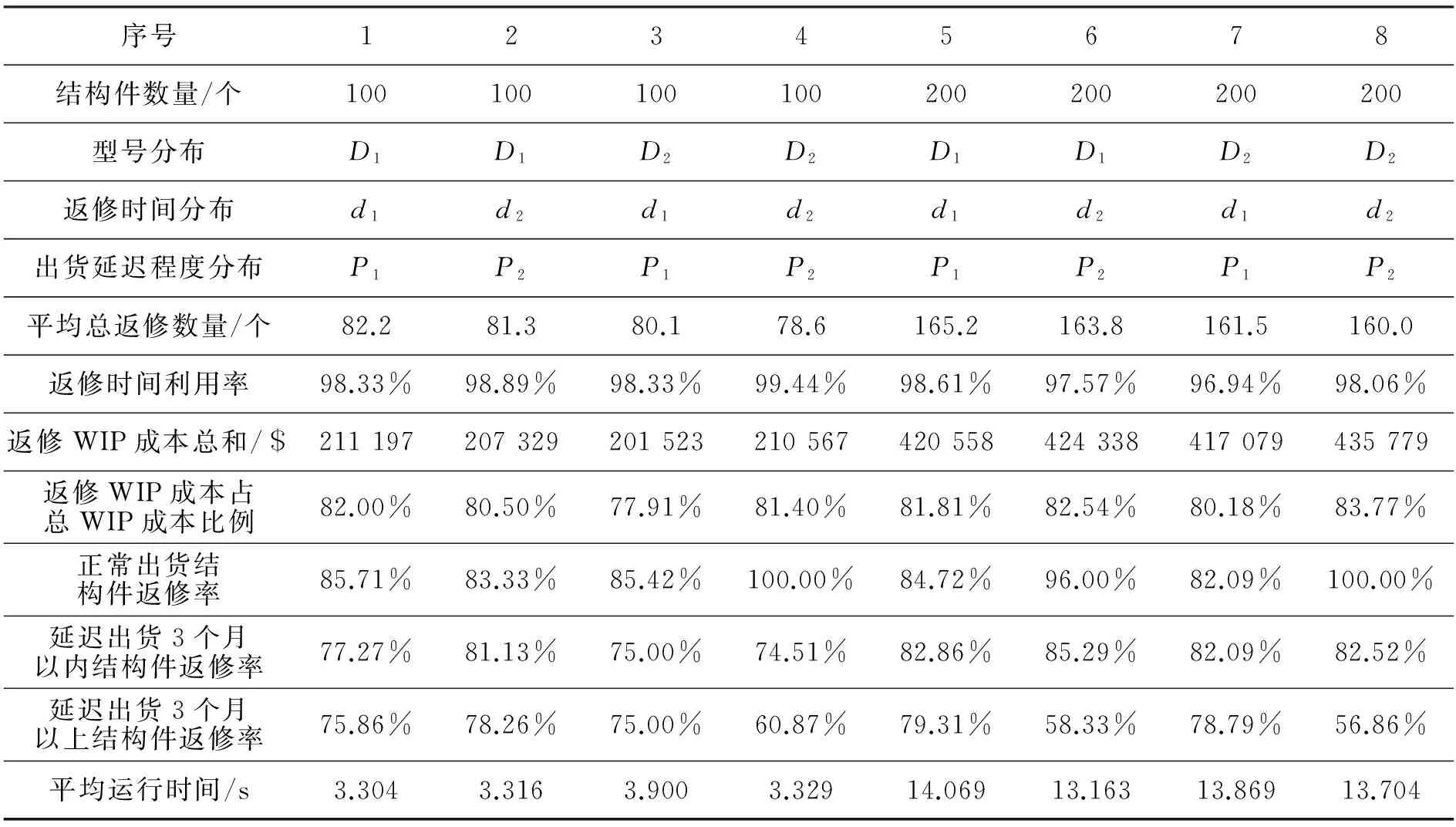
表7 算法一运行结果

表8 算法二运行结果

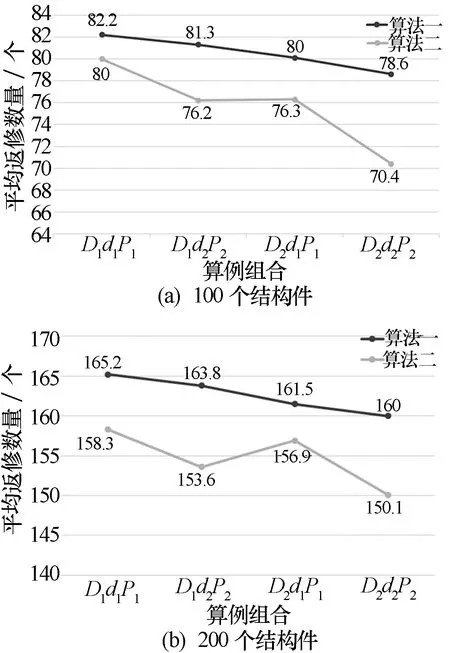
图2 平均返修结构件数量

从图2可以看出，无论是100个结构件，还是200个结构件，算法一的平均返修数量均高于算法二。进一步分析，在100个结构件情况下，对于4个算例组合，算法一比算法二分别高2.75%，6.69%，4.98%，11.65%；在200个结构件情况下，算法一比算法二分别高4.36%，6.64%，2.93%，6.60%。从上述数据中可以发现算法一和算法二最大差距为11.65%，最小差距也有2.75%。从算法一和算法二的伪随机选择机制来分析，造成这种差距的原因是算法二在启发式信息中增加了结构件返修紧急程度指数，蚂蚁会优先选择紧急程度指数大的结构件。而通常情况下，紧急程度指数大的结构件其返修时间也较长，所以算法二的平均返修数量低于算法一。

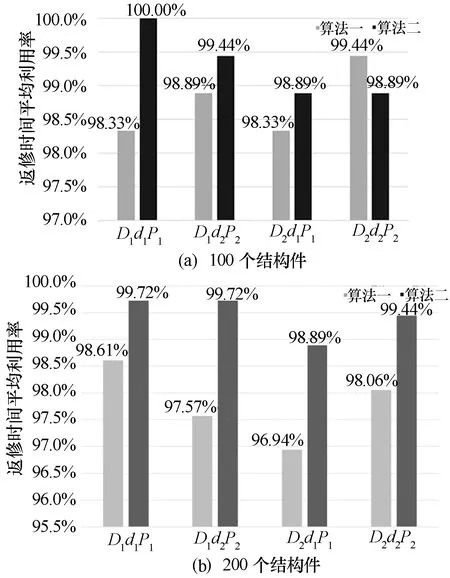
图3 返修时间平均利用率

从图3可以看出，在100个结构件，D2d2P2算例组合情况下，算法一的时间利用率高于算法二0.55%，其余情况下，算法二的时间利用率均高于算法一。算法一和算法二全部算例的平均返修时间利用率分别为98.27%和99.10%，均大于98%，两者之间相差不大。

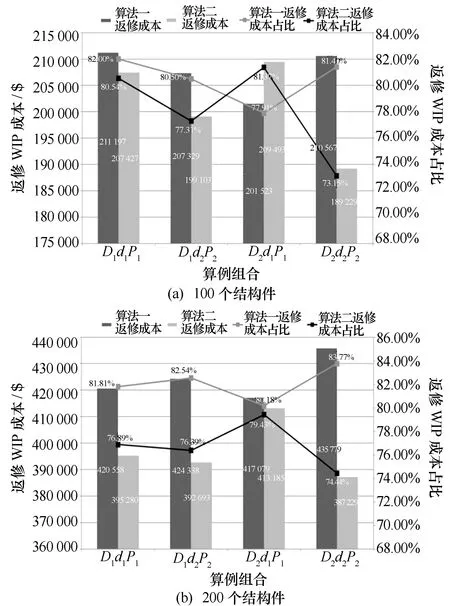
图4 返修WIP成本和返修WIP成本占比

从图4可以看出，通常情况下，算法二的返修WIP成本都比算法一小，只有在100个结构件，D2d1P1算例组合的情况下，算法二的返修WIP成本才略大于算法一。从返修WIP成本占总WIP成本比例来看，100个结构件的情况，算法一的均值为80.45%，算法二为78.09%，算法一同比增加2.36%；200个结构件的情况，算法一的均值为82.08%，算法二为76.79%，算法一同比增加5.29%。因此在返修WIP成本方面，算法一要优于算法二。另外，算法一平均运行时间为3.46s(100)和13.70s(200)，算法二为64.42s(100)和505.93s(200)。二者之间差异较大，其中运行时间最大值为505.93s，对于在返修时间段只进行一次的返修计划来说，2个算法都是可以接受的。

如图5所示，结构件数量为100时，2个算法的3种出货延迟等级的结构件返修率有一个明显的趋势，即算法一的正常出货结构件返修率均大于算法二的相应返修率；在图5(b)中，算法一和算法二互有输赢，没有明显的优劣趋势；在图5(c)中，算法一延迟出货3个月以上的结构件返修率都小于算法二的相应返修率。在图6中，结构件数量为200时，也有同样的趋势。

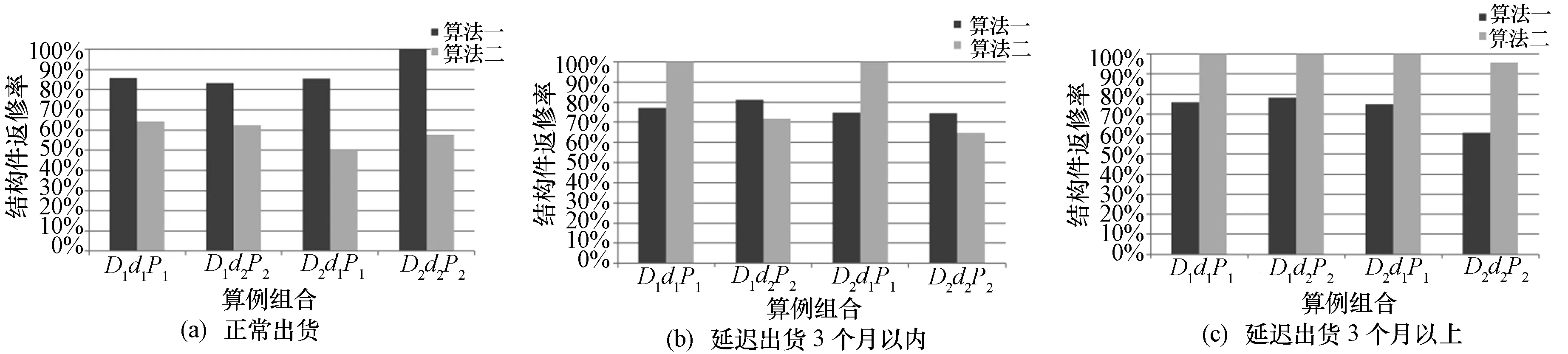
图5 结构件数量为100时3个出货延迟等级结构件返修率

从具体的数值来看，算法二延迟出货3个月以上结构件的平均返修率为98.19%(100)和100%(200)，而算法一只有72.5%(100)和68.32%(200)。至于延迟出货3个月以内结构件的平均返修率，算法一为76.98%(100)和83.19%(200)，算法二为84.1%(100)和83.92%(200)。因此可以得出结论，算法二计划返修更多的出货紧急的结构件。

4 结束语

本文研究了返修工序的计划问题，通过综合考虑返修时间、返修时段、WIP成本和出货延迟程度等相关约束，确定了在给定返修时段内最大化返修结构件数量的目标。在确定了目标的基础上，对返修工序的计划问题进行了数学建模，给出了一个0-1整数规划模型，并采用蚁群算法对该模型进行求解，在蚁群算法中设计了两种不同的伪随机选择规则，按照实际累积结构件的情况设计了相关算例，并针对两个蚁群算法，计算并验证了上述算法。通过算例分析，得出如下结论：

1)在最大化返修结构件数量方面，算法一的表现优于算法二。

2)在返修时间利用率方面，2个蚁群算法并无显著差异。

3)在减少公司WIP成本方面，算法一的表现优于算法二。

4)在正常出货结构件返修率方面，算法一计算结果优于算法二，但在权重较大的延迟出货3个月以内和以上结构件返修率方面，结果相反，算法二计算结果更佳。从总体上来讲，算法二计划了更多的出货紧急的结构件，而算法一计划了更多正常出货的结构件，因此算法二的计算结果更好。

综上所述，考虑到目前G公司的实际情况，即累积了大量的待返修结构件，已经没有足够空间来安全存储新的待返修结构件，同时大量的待返修结构件带来了严重的WIP成本和出货压力。目前的重点是尽可能多地返修结构件，以避免发生结构件无处存放导致受损或正常生产结构件的存放受影响的情况。因此将返修计划分为两个阶段，第一阶段采用算法一进行返修计划，在解决存放空间不足的问题后，第二阶段采用算法二进行返修计划，以达到减少WIP成本和出货延迟情况的目标。

[1] 马晓坤, 杨晓峰, 姜婧, 等. 热固性碳纤维预浸料用环氧类基体树脂[J]. 弹性体, 2013(3): 83-88.

[2] 唐桂云, 王云飞, 王宝瑞. 碳纤维复合材料蜂窝夹层结构的无损检测方法研究[J]. 纤维复合材料, 2011(1): 30-32.

[3]KATNAMKB,DASILVALFM,YOUNGTM.Bondedrepairofcompositeaircraftstructures:Areviewofscientificchallengesandopportunities[J].ProgressinAerospaceSciences, 2013, 61: 26-42.

[4] RICCIO A, DI FELICE G, SCARAMUZZINO F, et al. A practical tool for the preliminary design of bonded composite repairs[J]. Applied Composite Materials, 2014, 21(3): 495-509.

[5] COLORNI A, DORIGO M, MANIEZZO V. Distributed optimization by ant colonies[C]//Proceedings of The First European Conference on Artificial Life, 1991, 142: 134-142.

[6] DORIGO M, MANIEZZO V, COLORNI A. The ant system: an autocatalytic optimizing process[R]. Technical Report, 1991.

[7] DORIGO M, STÜTZLE T. Ant colony optimization[M]. London: The MIT Press, 2004.

[8] 崔海坡, 温卫东, 崔海涛. 复合材料层合板冲击损伤及剩余强度研究进展[J]. 材料科学与工程学报, 2005, 23(3): 465-472.

姚智骞(1992-)，男，硕士研究生在读，主要研究方向为生产计划调度。

Repair Scheduling for Composite Structural Parts Based on Ant Colony Algorithm

YAO Zhi-qian

(SchoolofMechanicalEngineering,SoutheastUniversity,Nanjing211189,China)

In order to solve the quality defects problem of composite structural parts in manufacturing, G Company sets up a repair process. For the scheduling problem in the repair process, a 0-1 integer programming model is developed with the objective of maximizing the number of repair parts. The shipping delay and high WIP cost are considered at the same time. Two pseudo-random selection mechanism are proposed based on ant colony algorithm. Problem instances with different parameter combinations are used to test the performance of the proposed algorithms. Computation results show that algorithm one is better in aspect of repair parts number, but algorithm two outperforms algorithm one in terms of reducing shipping delay and WIP cost.

repair scheduling; integer programming; ant colony algorithm; pseudo-random selection mechanism

2016-11-18

TH166；TH18

A

1008-5300(2017)02-0048-08