贝叶斯网络故障诊断的先验概率评估研究*

陈强强，陈志平，李春光，唐艳同，黄超亮

(1. 杭州电子科技大学， 浙江 杭州 310018； 2. 绍兴市特种设备检测院， 浙江 绍兴 312000)

贝叶斯网络故障诊断的先验概率评估研究*

陈强强1，陈志平1，李春光1，唐艳同2，黄超亮2

(1. 杭州电子科技大学， 浙江 杭州 310018； 2. 绍兴市特种设备检测院， 浙江 绍兴 312000)

针对贝叶斯网络中引入专家意见的先验概率准确度问题，对专家意见的误差判别、量化规则、意见综合等方面进行了研究。基于多重插补法对故障样本中的缺失统计数据进行概率插补，利用MATLAB进行概率拟合后得到了完备的先验概率集，提出了一种系统化的专家先验概率评估方法，并应用于大型桥式起重机故障诊断，验证了先验概率评估方法的可靠性。研究结果表明，该评估方法能够实现专家定性意见的精确量化，可以有效减小先验概率误差、提高故障诊断的效率，也可为先验概率赋值合理性的进一步研究提供依据。

先验概率；误差判别；精确量化；概率插补

引 言

贝叶斯网络是故障诊断系统中常见的推理算法，网络根节点先验概率的准确程度直接决定其能否快速定位第一故障点。然而，当统计先验概率的样本有限时，以统计概率替代先验概率的精确度就会大打折扣。解决这种问题的一般做法是引入专家意见，但是引入专家意见后又会导致其他问题：如何剔除专家意见中的误差，如何融合专家组意见等。

目前国内外对先验概率的赋值评估做了大量研究，文献[1]提出基于模糊先验概率的期望效用模型，该模型主要研究评价人的心理因素在某方面的影响；文献[2]提出先验概率和似然函数未知时的分布式检测融合方法；文献[3]提出了计算先验概率的最大熵方法；文献[4]提出通过改变专家权重对专家意见先验概率进行修正；文献[5]提出了一种改进的先验概率粗糙集模型；文献[6]提出了一种特征曲线法获取图像形式的先验概率，并用于预测日本的竹林空间分布。然而上述研究并不适合评估引入了专家意见的故障诊断先验概率，尚不能解决专家意见如何精准量化的问题，尤其是当故障诊断样本容量不足时还会造成故障底事件的统计先验概率缺失。如何获得完备、准确的先验概率集值得进一步研究。

针对以上问题，本文将对贝叶斯网络故障诊断的先验概率评估进行研究，提出一套系统的处理先验概率赋值的方法，并以大型桥式起重机为例，对其故障解耦后得到的故障底事件进行分析，验证先验概率量化插补的重要性。以期提高先验概率赋值的准确性，提高贝叶斯网络故障推理的可靠性，为贝叶斯网络故障诊断在大型设备上的广泛应用奠定基础。

1 先验概率赋值误差判别方法

专家在对先验概率赋值时，难免会产生误差，此时需要对误差来源进行研究分析，对误差进行分析鉴定，在故障诊断系统中给予专家引导性提示，以达到尽可能提高先验概率数据来源准确度的目的。

1.1 误差分类

自然界中，误差通常分为系统误差和随机误差。同样，对于一个给定的故障结果Q，存在可能造成此故障结果的故障底事件q1,q2, …,qn。专家依照实际诊断时的经验，对各故障底事件的可能性进行赋值。在此过程中，专家的经验诊断评价也存在评价失真误差和评价经验误差。前者是考虑到专家在对先验概率赋值当天受情绪、身体状态、心态等隐性因素影响导致赋值失真，属于随机误差。后者是由于桥式起重机故障原因复杂，专家的知识领域又各有不同，所以得到的专家评价仍可能出现因经验不足引起的赋值粗大误差，属于系统误差。

1.2 误差认定

1.2.1 评价失真误差认定

为了避免专家偶发性诊断失常，让专家每隔24 h对Q的故障底事件进行可能性打分排序，重复3次并采集数据。为了将失真误差放大以便更好地辨别，将采集后的数据重复扩充一倍，若存在系统误差，则经此处理后误差将具有周期性出现的特点。

首先用贝赛尔公式计算标准差：

(1)

式中，vi表示残差，此时利用阿贝-赫枚特判别法，对残差vi做统计量：

(2)

若：

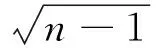
(3)

则怀疑存在评价失真误差。

1.2.2 评价经验误差认定

首先将不存在评价失真误差的专家赋值结果汇总。由于专家库有限，专家评价数据是一个较小的样本，且每个专家评价意见都十分重要，不可随意剔除，针对这一特点选用格罗布斯准则和肖维勒准则[7]联合评判，以提高判别可靠性。

表1 肖维勒系数

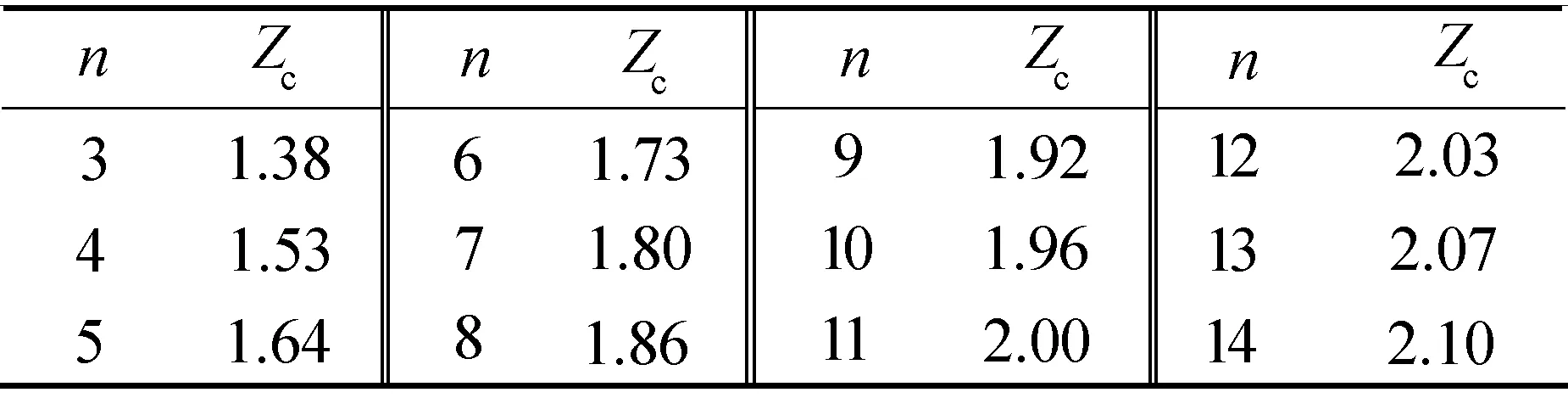
根据图1所示联合评判法则，认定专家评价是否存在评价经验误差，若存在则需要进行剔除或修正。

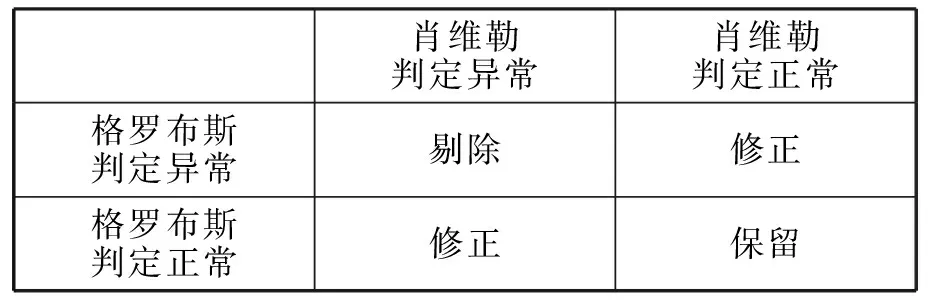
肖维勒判定异常肖维勒判定正常格罗布斯判定异常剔除修正格罗布斯判定正常修正保留

图1 联合评判法则

2 基于插补法的先验概率量化补全

2.1 专家定性赋值规则

贝叶斯故障诊断网络的故障根节点需要准确的先验概率，而实际中专家凭借自己的诊断经验并不能对故障底事件给出定量的概率值。对桥式起重机进行模块分解后搭建的贝叶斯网络模型如图2所示。可见每个故障底事件对应的故障根节点数目不超过9个，因此将专家意见划分为9级能够满足故障概率排序集合的宽度要求。

图2 桥式起重机贝叶斯网络模型

专家可以根据诊断经验，按照表2给出故障底事件可能性的评分值。一级表示发生最频繁(即最可能导致故障底事件)，依级递减。

表2 故障发生概率等级对应评分

2.2 基于分批估计理论的专家意见拟合方法

根据算术平均值和分批估计理论，对于每个故障底事件，筛选符合条件的多个专家给出的可能性评价进行分批处理。由于专家库评价样本不大，分成2批处理基本可以满足要求，最后进行数据融合。

对分批后的每组数据求算术平均值T1、T2，标准差σ1、σ2，得到融合值：

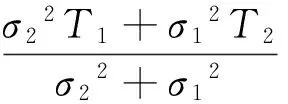
(4)

2.3 专家经验不确定度计算

初始条件下，各专家可视为等精度评价(即诊断评价权重相等)，首先计算A类不确定度UA=kpb，kp为包含因子，b为算术平均值的标准偏差：

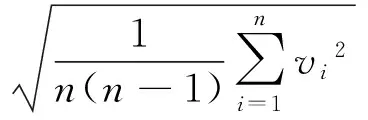
(5)

一般误差都符合正态分布，表3列出了部分置信水平P与包含因子kp的关系。

表3 置信水平与包含因子关系

再计算B类不确定度UB=a/k，a为置信区间，k为相应的包含因子。

2.4 基于多重插补法的先验概率定量转化

受限于桥式起重机故障诊断样本容量，有可能会出现故障底事件发生概率统计缺失的情况。但是在理想状态下，专家的经验诊断应该与统计概率存在相关关系，因此采用多重插补法进行缺失数据的概率插补。

多重插补法[8]的理论证明来源于贝叶斯理论，它由Rubin在80年代初期以一系列论文提出，其主要思想是给每个缺失值都构造m个插补值(m>1)，这样就产生出m个完全数据集，对每个完全数据集使用相同的方法分别进行处理，得到m个处理结果，最后再综合这m个处理结果，最终可以得到对目标变量的估计。

将专家的最终诊断评价P作为辅助变量，由样本计算出的具体概率Y作为目标变量，多重插补法具体操作步骤如下：

(1)插补

假设故障底事件的个数为6，将故障底事件按照对应专家评价值从小到大排序，最终得到的先验概率数据集存在2处缺失，即Y2和Y5缺失，如表4所示。

表4 故障底事件概率统计

因为具体概率Y和专家的最终诊断评价P存在相关关系，假定采用最近距离法为每个缺失值插补2次，即m等于2。第1个缺失值的辅助变量为P2，取与其距离最近的P1和P3对应的具体概率Y1和Y3作为其插补值，对第2个缺失值做同样处理。最终形成2个完整数据集。

(2)分析

(6)

式中：f按照采集的诊断数据的样本容量大小取值，一般取0.1～0.3；n为故障底事件的例数；其他各参数计算如下：

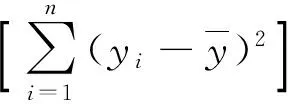
(7)

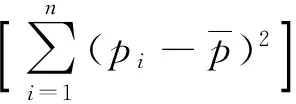
(8)

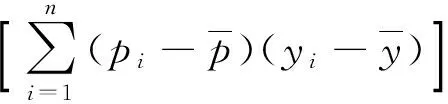
(9)

(3)合并

将分析得到的数据进行合并，即：

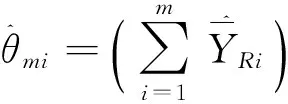
(10)

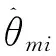
(11)

其中插补数据集内的方差：

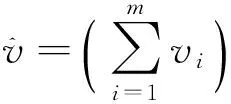
(12)

插补数据集间的方差：

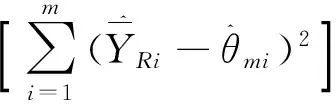
(13)

最后便可估算出缺失数据的置信区间。

3 实例验证

以桥式起重机制动器故障底事件举例，邀请了4位专家分3次对故障底事件发生概率的可能性进行定性赋值，记录结果如表5所示，并根据表2将其转化为评分。

表5 专家分次定性评价记录

3.1 误差判别

利用式(1)～式(3)检验各专家对各底事件的评价失真误差，以制动瓦衬为例，计算过程如表6所示。

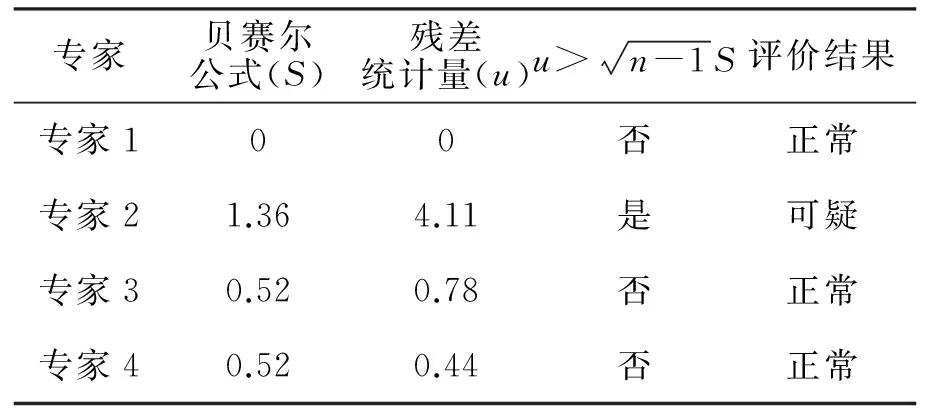
表6 制动瓦衬评价失真误差检测记录

根据表6的评价结果，专家2在对制动瓦衬的发生概率评价时可能存在评价失真误差。观察原始记录可见专家2在3次评价时所给的等级均不同，且最大相差三级，应该向专家重新确认修正。对其他故障底事件同样进行评价失真误差的判别和修正。

利用格罗布斯准则对修正后的数据进行检验，在所得检验结果基础上再进行肖维勒准则判别，结果如表7所示。

表7 专家组评价失真误差鉴定结果

3.2 专家评价结果表示

将修正后的专家评价结果分为2组，利用式(4)进行数据融合，根据需要取置信水平为0.9，此时kp取值为1.645，计算总体不确定度，得到最终结果如表8所示。

表8 含不确定度的专家组意见

3.3 先验概率插补

通过对采集的故障样本数据的分析，得到各故障底事件初始的统计故障概率，如表9所示。

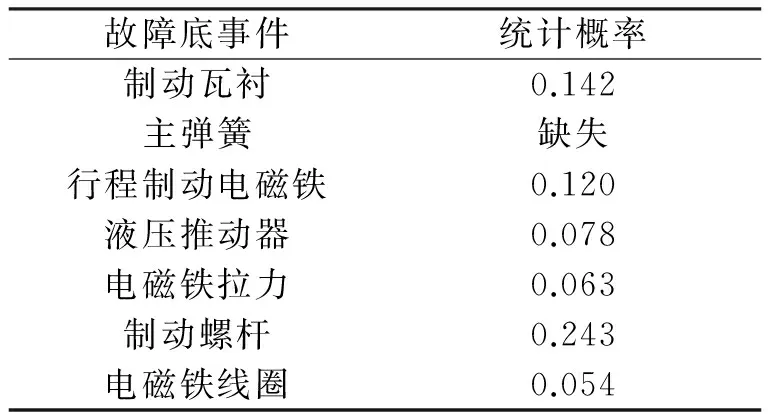
表9 故障底事件初始统计概率

可见，主弹簧故障概率在统计的样本中并没有出现，即出现概率缺失情况。此时将故障底事件按发生等级进行排序，采用最近距离法对缺失数据进行插补，结果如表10所示。

根据式(6)～式(13)，插补的缺失概率最终可表示为：

3.4 先验概率拟定

为了更好地综合专家评价和综合补全后的统计概率，需要对两种数据进行二次关联。利用MATLAB中的cftool工具箱进行曲线拟合，对比多种拟合方程，选定幂函数拟合，最终结果如图3所示，拟合残差如图4所示。

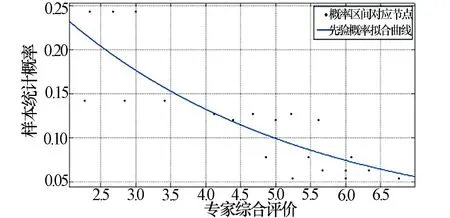
图3 先验概率拟合曲线

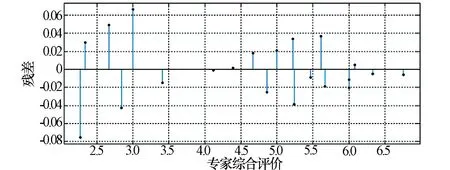
图4 先验概率散点残差分布图

拟合后的相关系数达到0.8，由于前文已经给出统计概率对应的专家评价等级置信区间，因此可以认为此拟合模型具备可靠性。

利用拟合的曲线，将专家对各故障底事件的综合评价值代入，在曲线上即可定位先验概率，结果如表11所示。

表11 先验概率综合量化概率结果

由表11可见，最终拟合的先验概率满足概率故障等级递减的规则，在统计概率的基础上融合了专家的评价意见，且结果呈现出故障等级越高，概率变化量越小的规律，也符合实际诊断中对于发生概率极低的一些故障底事件较难判定优先级的情况。

4 结束语

1)通过对专家意见中出现的评价失真误差及评价经验误差进行判别修正，提出基于分批估计理论的专家意见拟合方式，减少了人为评价中不利的主观干扰，提高专家评价可信度。

2)考虑到定性评价转换为定量评分时的误差，在专家定性评价中引入总体不确定度，再利用拟合曲线得到量化的先验概率。

3)在统计概率存在缺失的情况下，利用专家综合评价作为辅助变量，提出基于多重插补法的概率插补模式，有效地补全了初始先验统计概率。

4)在诊断样本有限的情况下，提出融合统计概率和专家意见进而得到先验概率集的评估方法，提高了先验概率赋值精度。

本文提出了一整套关于先验概率定量评估的方法，随着诊断数据样本的增加，先验概率还需要实现不断修正，因此在下一步的工作中，将对先验概率自学习模式深入研究。

[1] 王愚, 达庆利, 陈伟达. 基于模糊先验概率的期望效用模型[J]. 管理科学学报, 2002(3): 30-34.

[2] 王国宏. 先验概率和似然函数未知时的分布式检测融合[J]. 电光与控制, 2004(1): 10-14.

[3] 孟晓风, 季宏, 王国华, 等. 计算故障先验概率的最大熵方法[J]. 北京航空航天大学学报, 2006(11): 1320-1323.

[4] 陆静, 王捷. 基于超级贝叶斯方法的专家意见先验概率修正研究[J]. 统计与决策, 2013(1): 15-18.

[5] 陶志, 刘彩平. 一种改进的先验概率粗集模型[J]. 中国民航大学学报, 2014(4): 48-51.

[6] HARA N, SHIMAZAKI H. Using informative prior probability to estimate bamboo forest distributions in Japan[C]//Asian Association on Remote Sensing, 2015.

[7] 刘渊. 误差理论与数据处理[D]. 大连: 大连理工大学, 2008.

[8] 沐守宽, 周伟. 缺失数据处理的期望-极大化算法与马尔可夫蒙特卡洛方法[J]. 心理科学进展, 2011(7): 1083-1090.

陈强强(1993-)，男，硕士研究生，主要从事机电一体化、精准测量等方面研究工作。

Study on Prior Probability Assessment of Bayesian Network Fault Diagnosis

CHEN Qiang-qiang1，CHEN Zhi-ping1，LI Chun-guang1，TANG Yan-tong2，HUANG Chao-liang2

(1.HangzhouDianziUniversity,Hangzhou310018,China； 2.ShaoxingSpecialEquipmentInspectionInstitute,Shaoxing312000,China)

Aiming at the problem of the accuracy of prior probability when introducing expert-opinions into Bayesian network, the article studies expert-opinion error determination, quantitative rule, opinion synthesizing, and so on. The probabilities of absent samples are calculated based on multiple interpolation method. A complete set of prior probabilities is obtained by probability fitting using MATLAB. A systematic expert prior probability assessment method is proposed and is applied to the failure diagnosis of large bridge crane, and the reliability of the method is thus verified. Research results indicate that this method is able to quantify the qualitative opinions of experts accurately, reduce the prior probability error effectively and improve the efficiency of failure diagnosis. It is well expected that this work will provide a strong basis for further research on the rationality of prior probability assignment.

prior probability; error determination; accurate quantification; probability interpolation

2016-08-31

国家质量监督检验检疫总局科技计划项目(2015QK082)；国家质量监督检验检疫总局科技计划项目(2015QK273)；浙江省自然科学基金资助项目(LY12F02004)

O212.8

A

1008-5300(2017)02-0056-05