基于改进蚁群算法的物流配送路径优化研究

邓 波，蒲保兴

(邵阳学院 信息工程学院，湖南 邵阳，422000)

基于改进蚁群算法的物流配送路径优化研究

邓 波，蒲保兴

(邵阳学院 信息工程学院，湖南 邵阳，422000)

物流配送行业不但要求所有货物能及时进行配送，而且也要求尽可能降低整个物流运输成本。所以物流配送车辆路径优化问题是重点亟待解决的关键问题，由于传统的优化方法搜索时间较长，且难以找到全局最优路径，从而造成配送成本高，效率低。为了降低成本，提高车辆路径优化率，本文以蚁群算法为基础，并加以改进，首先建立优化物流配送路径的全局数学模型,然后采用改进信息素更新规则、改进启发信息更新策略获取最优物流路径，通过优选算法参数，改进蚁群算法对全局数学模型进行求解。从而有效避免只有局部优化解的出现。仿真实验结果表明，改进后的算法效率提高较大，算法在实验环境下收敛性好，是解决物流配送路径优化问题的有效算法。

物流配送；蚁群算法；路径优化；仿真；VRP

随着社会实体经济的高速发展，整个物流行业也得以快速发展，物流行业中的物资配送越发成为当今企业生产过程中一个非常重要环节，物流配送指的是依照用户的订单要求,并在配送中心进行准确地分货、配货，然后将配好的货物及时送交给用户的活动[1]。由于油价、人力资源等成本的不断上涨，物流运输费用已逐渐成为商家成本主要部分，又由于现代拥挤的城市交通与及时物资配送服务之间存在着难以调和的矛盾，因而优化物流车辆路径相对于整个物流效益、速度以及运输成本都显得至关重要，因此怎样选择最优配送路径，及时将货物配送到用户手中，也已成为物流行业相关领域里的关键问题[2]。

配送车辆路径问题(vehicle routing problem，VRP)的关键是整个物流系统优化环节。通过系统选择配送车辆的最佳输送路径，并对运输车辆调度进行优化，合理安排配送车辆配送顺序，可以减少车辆的行驶距离和空驶率。在物流配送中，存在很多决策优化问题(例如距离、时间、费用等)[3]，大部分仅探讨物流配送路径的优化问题，即在满足客户需求的前提下，制定出合理的货物配送路径，通过派遣数量最少的车辆并为配送车辆指派运输时间和运输最省的路线费用，迅速地将货物输送客户手中。优化配送路径其实是一个NP问题，只有当客户节点和线路较少时，才能求得精确解，然而当问题的规模增大时，精确求解会存在耗时较长，并且效果低现象；而采用人机互动法，又需要管理者具备足够的物流配送专业知识，且会增加对车辆配送路径选择的随意性[4]。对于这类问题的求解一般应采用启发式算法，该算法是指通过对已经解决具体问题的经验不断进行归纳、分析、推理，并产生解决此类问题的方法[5]。其目标是在适当的代价下得到即将要解决的全局问题的满意解或最优解，这样不但节省了时间，也会满足用户的实际要求。又由于启发式算法具有效率高、实现简单等多种优点，所以引起了当今优化研究领域的广泛关注，近年来发展非常快。

蚁群算法是一种群智能优化算法，该算法是通过正反馈并行机制和蚂蚁间协作定能找到巢穴与食物之间的最短路径[6]。蚁群算法一被提出就受到研究领域的广泛关注，因为该算法不但具有并行性好、求解速度快等优点，而且在解决路径优化、任务分配等方面表现出优良的性能，但是蚁群算法同时也存在一定的缺陷，例如当问题变成大规模时，就会出现运算时间长、收敛速度较慢、容易陷入局部最优解等现象[7，8]。

1 构建VRP数学模型

假定某个物流公司具有N个客户以及M个集散中心，物流车辆配送路径的目标是要在使配送成本最小的情况将货物从M个集散中心送到N个客户点上。在车载量q和客户需求量gi(i=1,2…n)均已知的前提下，可以确定至少应派多少台车才能满足应用需求且车辆所经的总路径最短，从而找到配送方案中最小成本的方案，在进行数学模型构建时首先作如下假设：

1)车辆对每个客户点服务，途中只卸货无装货的情况。

2)每一台配送车辆均以同一集散中心为起点和终点。

3)车载量要大于每条配送路径上客户量之和(q>gi)。

4)每辆车只服务一条路线，每一个客户只被一辆车配送。

5)每辆配送车所经过的路线均不能重复。

可以由下列公式求得所需车辆数目m:

(1)

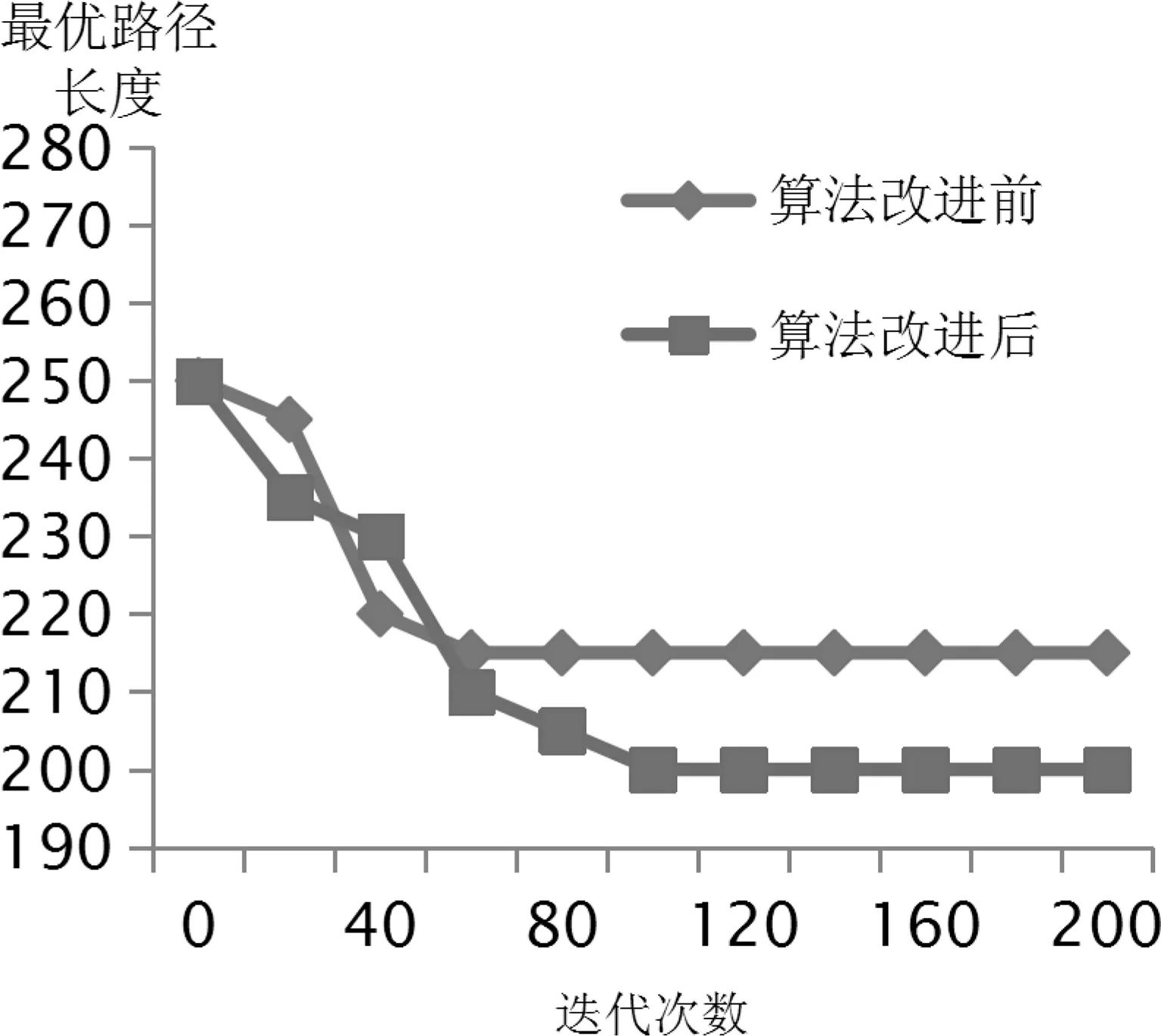
其中：m表示所选择车辆数，a是参数，且0

建立物流配送路径选择问题的求解数学模型。首先定义以下变量：

Xik=1 (客户i的配送由车辆k完成，i、K分别表示客户、车辆的编号)

(2)

或Xik=0 (客户i的配送车辆k未完成配送)

Yijk=1 (车辆k从i客户点行驶到j客户点完成)

(3)

或Yijk=0(车辆k从客户点i行驶到客户点j未完成)

(4)

minZ=∑i∑j∑kCijYijk

(5)

设置如下限制条件：

∑iYki=1i=1,2,…,m

(6)

∑iGiXki≤qi=1,2…,m∀k

(7)

∑jXkijk=Ykii=0,1,…,∀k

(8)

∑iYkijk=Ykjj=0,1,…,∀k

(9)

X=Xijk∈S

(10)

Xijk=0或1i,j=0,1,…,∀k

(11)

Yki=0或1i,j=0,1,…,∀k

(12)

上述条件约束了车辆的配送总容量，其中，Cij表示从点i到点j的所有运输成本，Gi表示任务i的运输量，q表示货物配送总容量，所有货物运输任务均由m台配送车辆去完成，保证每个客户的所有货物仅由唯一台辆车来配送完成，即保证了服务的唯一性[9]。

2 蚁群算法的改进

通过专家们多年来的研究，蚁群算法的应用研究已经取得了较大进展，在各种工程领域中得以广泛应用，但由于该算法收敛速度慢，且容易陷入局部最优解等多种缺点。作者力求通过对局部信息素更新规则的改进，优化组合动态调整相关参数和全局更新策略，实现算法优化，从而提高了蚁群算法的收敛速度，达到了增强全局搜索的随机性，极大地抑制了算法出现早熟现象。

2.1 信息素更新规则改进

在所研究基本蚁群算法中，发现存在两种信息素更新策略，即实时更新、全局更新。前者是指蚂蚁在从一个节点完成到达另一节点后，就马上更新路径的信息素;而后者是指蚂蚁在遍历完所有节点后才更新整条路径上的信息素。这两种方式相比较，全局更新策略可以迅速加快收敛速度。目前很多研究已表明全局更新效果好，但同时也有一些缺陷，例如该方法下全局更新通常收敛过早，在同一条路径上会使大量蚂蚁很快集中，从而无法发现和得到更优解，也即陷入局部最优解情况[10]。

在信息素更新过程中，系统通常只会更新找到最优路径的蚂蚁的信息素。对于这只蚂蚁信息素的更新，通常可采用以下两种方式进行，一种是在循环过程中找到表现最佳的蚂蚁，该方式的收敛速度通常比较慢，不会过早导致迅速收敛到某条路径上，蚁群还会继续去找新的路径，也就更易于去发现更好的路径；另一种则是找到在整个运算中表现最佳的蚂蚁，该更新方式可以迅速提高收敛速度，从而得到较优解，但这也阻碍了蚁群再去寻找更优解，容易使整个蚁群困在相对较差的某路径上。因此，本文提出了一种新的混合更新信息素策略，也即在搜索前几次循环过程中，采用迭代最优法不断进行及时信息素更新，进行信息素更新是为发现本轮循环中表现最佳的蚂蚁，该方法通常可方便找到很多较优解，可有效避免蚁群过早陷入到较差解中；经多次循环(在此以十次循环为例)完成更新以后，然后再采用全局最优解进行更新，也即信息素更新是利用整个运算以来最佳表现的蚂蚁来进行的。在混合信息素更新规则被采用后，本算法会收敛到较优解集中，从而也就可以找到更多可行解，并且还能继续去搜寻其他更优解，并且保持着快的收敛速度，可有效地去克服采用单一全局更新时易过早出现陷入局部最优解的不足。

改进后信息素更新规则如下:

τij(t+1)=(1-ρ)×τij(t)+Δτbest

(13)

其中：Δτbest= 1 /f(sbest)；全局最优解sob用f(sbest)、本次迭代所得最优解用sib表示。再则为了防止搜寻停滞，应将路径上的信息素限定在某个可以预定的范围之内，而对于全部信息素τij(t)都必须满足

τij(t)∈[τmin，τmax]，如果τij(t)≥τmax，那么将设置为τij(t)=τmax，如果

τij(t)≤τmin，那么将设置为τij(t)=τmin，如果在某个迭代过程中产生了可行解，且其信息素的量是τmax，而其他路径上信息素的量却是τmin，那么收敛就会出现。可以动态地按照以下策略进行信息素的改进：

1)在初始状态下，信息素未加以更新，采用式(7)、(8)来确定初始更新范围，其中L(sbest)表示全局最优解或本次迭代所得最优解，而每次迭代运算过程中出现新增的信息素最高值则用1 /L(sbest)表示。

(14)

(15)

2)若信息素更新完成后，则开始采用式(16)来确定τmax(t)，而τmin(t)仍采用式(15)来确定。

(16)

2.2 启发信息更新策略的改进

在进行路径规划时，可以根据式(5)来进行相应路径选择，但式(5)中只反映了当前结点与其相邻接结点之间的关系，并没有反映出其邻接结点与终点之间的关系，它搜索的空间是以起点为中心近似圆形的区域，由于这种没有方向性的搜索很容易造成搜索失败或收敛速度过慢等原因。为此，可将与当前结点i相邻的下一可选结点j到终点z的直线距离djz引入启发函数，这样得到

(17)

定义在t时刻第k只蚂蚁从位于节点i上选择下一个j节点为目标的概率为:

ifj∈allowedk

(18)

这里,ηij是由i转移到j的启发信息，由要解决的问题函数给出。参数α和参数β分别用来表示控制信息素浓度以及启发信息相对重要程度。而allowedk表示第k只蚂蚁下一步可选择所有节点的集合[11]。

通过将djz引入到启发函数，改变了无向搜索，使搜索的方向性加强，搜索的空间也转化为由起点到终点的椭圆形区域，缩小了搜索区域，搜索的成功率大大提高，然而，对于实际道路交通状况，由于交通环境(如快速路、高速路)等因素的影响，该方向启发的方法并不一定得到最优路径，这是因为方向启发的过早所致，使得初始搜索空间有限，为此，特引入当前结点i与起点o之间的直线距离dio作为初始搜索空间的大小，等搜索到一定的程度以后再引入方向启发进行搜索空间缩减，从而在利用蚁群算法进行路径规划时，首先应按基本蚁群算法去进行路径搜索，当距离dio大于给定的阈值ε时，应采用式(15)来进行具有方向启发的路径搜索，确定了方向，不仅提高了搜索到最优路径的可能性，而且也尽可能地缩减了搜索空间，因此提高了该算法的执行效率[12]，对于起点o与当前结点i的直线距离阈值ε应根据地方区域规模来加以确定，常见的方法是参照起点o与终点z直线距离dOz进行确定。

3 改进后的蚁群算法实现步骤

算法改进后的详细流程实现步骤如下:

步骤1 首先对参数进行初始化。设Nc= 0(Nc表示迭代次数)，并设置最大迭代次数为Ncmax，初始化信息素强度Q，设置最大信息素强度为τmax、最小信息素强度为τmin和α、β的值，每条路径上的信息素浓度值τij(0)=c(c为常数)，并设置Δτij= 0，然后随机将m个蚂蚁放置到初始点上。

步骤2 设置循环搜索次数Nc，其值变化趋势Nc=Nc+ 1。

步骤3 设置蚂蚁禁忌表，将禁忌表的索引号设成n，并且n= 1。

步骤4 设置蚂蚁数目m，其数目的变化趋势为m=m+ 1。

步骤5 确定搜索热区，判断某路径是否在热区以内，然后计算出每一只蚂蚁移动到下一条路径的概率值。

步骤6 当蚂蚁从某节点i出发到达下一节点j时，应当对其所经全部路径上的信息素及时进行更新并及时修改禁忌表，然后按照当前状况将修改禁忌表值，并将新节点j也置于禁忌表中。

步骤7 循环执行步骤 2到步骤 6 ，一直到每只蚂蚁都能找到一条包含区域内所有节点的可行路径。

步骤8 并在新搜索到的所有可行解集内产生一条最短路径，即这条路径就是本次迭代产生的最优路径。

步骤9 不断判断循环次数Nc，只要循环次数没有超过十次，则一直对蚂蚁所找到的最优路径依照本迭代最优值法去进行信息素更新；如果循环次数已经超过十次，则立即按照全局更新进行信息素更新。

步骤10 对全部蚂蚁经过的任何一条路径，都必须按式(11)到(14)进行一次全局更新信息素。

步骤11 重复执行步骤2到步骤7 ，直到在连续的多次迭代中没有出现更优解或者次数Nc的值已经达到最大的迭代次数Ncmax，才停止运算，然后将当前值作为算法最优解。

4 仿真实验研究

通过以上对算法加以改进和详细流程的介绍，本实验将用测试数据对改进后的蚁群算法进行仿真，通过对测试结果进行分析，评价改进算法的好坏。

4.1 数据集

已知某物流公司的有 8台配送车，每台车的最大载重量为10吨，每台车的最大行驶距离100公里，需同时向 30个客户提供服务，物流配送中心与客户的基本资料及位置情况如表1与图1所示。

表1 客户基本资料表

4.2 仿真平台及参数优化设置

仿真系统的运行平台为：CPU为2.6GMHz，内存为4GB，OS为windows 7，采用VB6.0 语言编程实现。蚁群算法的参数设置如下：蚂蚁最大数目为100，α= 1，β= 1.5，实验进行了10次，最大迭代次数为 200，ρ= 0.85。

图1 客户地理位置信息图Fig.1 Customer location information map

4.3 仿真实验所得结果与分析

4.3.1 算法改进前后的最优车辆路径搜索结果

采用改进后的蚁群算法对最优配送路径进行求解，可用3台车3个路径即可完成，改进前，在迭代60次时，就产生局部最优解，最短路径为220公里，而改进后，按此算法在迭代100次时，就找到了问题全局最优解，最优路径长度为200公里，从仿真实例中可以看出，改进后，它能够以更快的速度收敛到全局最优解，也就是说本算法是一种有效的配送车辆路径优化方法。最短路径的收敛情况如图2所示。

图2 基本蚁群算法改进前后的收敛曲线Fig.2 The basic ant colony algorithm improves the curve of convergence before and after

4.3.2 算法改进前后对比分析

从图2可以看出，改进后的蚁群算法最优路径长度比改进前减少了20 km，而且收敛速度快了很多，所以无论是从收敛速度还是对最终结果进行比较，本文算法都要优于基本蚁群算法，基本蚁群算法容易停滞于局部最优解上的问题在改进后的算法中得到了有效的解决。可见，本文改进后的蚁群算法具有较大的优越性，也证明了改进后的蚁群算法的正确性和有效性。本例是在单一物流配送中心的情况下求解的，若是存在多个物流配送中心，则只需将多个配送中心通过分解法来进行区域划分，然后进行各自独立求解即可，所得解可能不是全局最优解，但仍然还是非常有效的、可行的。

5 结束语

物流中规划好车辆配送路径是提高物流企业经济效益的关键，本文通过对基本蚁群算法进行改进，包括启发信息更新的改进、信息素更新的改进等，设计出新的改进蚁群算法，针对物流系统当前存在的问题，对车辆路径优化问题进行了深入研究，并利用蚁群算并行性度、高法速度快、鲁棒性强的特点，创造性提出了基于蚁群算法的车辆配送路径优化问题的求解方法。在通过仿真实验对其进行验证后，其试验结果表明改进后的方法可以很好地提高效率，并能够非常快速地找到算法最优解，因而在以后车辆路径优化中肯定会展现出广阔的市场前景。

[1]唐炉亮，常晓猛，李清泉，等.基于蚁群优化算法与出租车GPS 数据的公众出行路径优化[J].中国公路学报，2011，24(2):89-95.

[2]余玥,胡宏智.基于改进遗传算法的物流配送路径求解[J].计算机技术与发展,2009,19(3):52- 55.

[3]CHEN Yaorong，LIANG Bo，ZHOU Meihua.Optimization for vehiclescheduling in iron and steel works based on semi-trailer swap transport[J].中南大学学报:英文版，2010，17(4):873-879.

[4]钟石泉，贺国光.有时间窗约束车辆调度优化的一种禁忌算法[J].系统工程理论方法应用，2005，14(6):523-527.

[5]CHAO Yiming.A tabu search method for the truck and trailer rou-ting problem[J].Computer and Operations Research，2002，29(1):33-51.

[6]姜宏岸，王刚.优先级队列的缓存管理机制的性能分析[J].计算机工程与应用，2009，45(25)：86-88.

[7]宋留勇，王锐，周永旺，等.动态城市交通网络优化模型研究及算法设计[J].测绘科学，2011，36(1):134-136.

[8]程明辉,齐名军.基于粒子群算法的物流配送路径优化问题研究[J].中国外资,2008,(8):254- 256.

[9]陈以,万梅芳.RBF神经网络在物流系统中的应用[J].计算机仿真,2010,27(4):159- 163.

[10]SEO JB，LEUNG V.Approximate queuing performance of amultipacket reception slotted ALOHA system with an ex-ponentialbackoff algorithm[C]∥4th International Conference on Communications and Networking in China，2009:1-5.

[11]杨中秋，张延华.改进蚁群算法在交通系统最短路径问题的研究[J].科学计算与信息处理，2009，32(8):76-78.

[12]KARSTEN M.FIFO service with differentiated queueing[C]∥7th ACM/IEEE Symposium on Architectures for Networking and Communications Systems，2011:122-133.

Logistics distribution path optimization research based on improved ant colony algorithm

DENG Bo,PU Baoxing

(School of Information Engineering,Shaoyang University,Shaoyang 422000,China)

Logistics industry can not only requires that all the goods in a timely manner and distribution,but also the requirement as far as possible to reduce the logistics cost.So the logistics distribution vehicle routing optimization problem is focused on the key problems to be solved,due to the traditional optimization method to search for a long time,and hard to find the global optimal path,resulting in the distribution cost is high,the efficiency is low.In order to reduce costs,increase the rate of vehicle routing optimization,in this paper,based on the ant colony algorithm,and improved it,the first to establish the mathematical model of the logistics distribution path of global optimization and then with the improved pheromone update rule,improvement of heuristic information update strategy,obtain the optimal logistics path,through the parameter optimization algorithm,ant colony algorithm for solving global mathematical model.Thus effectively avoid the occurrence of only local optimization solution.The simulation experimental results show that the improved algorithm efficiency is larger,convergence algorithm in experiment environment is good,and it is effective to solve the problem of logistics distribution route optimization algorithm.

logistics distribution;ant colony algorithm;path optimization;simulation;VRP

1672-7010(2017)04-0069-07

2017-04-21

湖南省科技计划项目(2012FJ3108)；湖南省教育厅科学研究项目(13C845)

邓波(1973-)，男，湖南邵阳人，讲师，硕士，从事嵌入式系统、数据挖掘研究蒲保兴(1965-)，男，湖南城步人，教授，博士，硕导，从事网络安全、数据挖掘研究

TP311

A