国际与国内高中数学课程教材内容的比较研究

温小英

摘 要：国内高中数学教材的内容少而精，对知识理论的掌握程度要求高，注重公式的精确应用和抽象逻辑思维的训练；国际高中数学教材的内容广而泛，跟实际生活联系很紧密，注重知识在实际生活中的应用，注重批判性和发散性思维的训练。

关键词：国际高中 数学课程 数学教材

一、问题的提出

近年来，国际教育热愈演愈烈，国际课程被纷纷引进，国际高中数学课程可以说是最热门的引进课程，引进的教材版本也各不相同，但内容和风格差不多。引进的这些数学课程教材跟国内的数学课程教材在内容的呈现方式上有什么不同呢？它对学生的思维方式的训练能起到什么作用呢？本文将结合本人的工作经历对国际与国内高中数学课程教材做简要的比较分析。[1]

二、国内与国际高中数学教材内容的对比分析

笔者从事国际高中数学课程教学七年有余，对国际O-LEVEL，A-LEVEL，SAT及IB数学教材有比较深入的研究，同时也将它们与国内普通高中的数学教材作了一番比较，发现国际数学教材的主要特点有：内容比较具体，覆盖面比较广，跟实际生活的联系很紧密，问题的设置上也比较直观，不需要很强的理论技巧。不需要很复杂的抽象思维，很少有复杂抽象的证明，更多的是形象有趣的生活应用。[2]

国际课程标准明确强调数学学习要保证学生变成有自信，有创新性的数学应用型人才和交流者；能够探究、呈现以及解释工作中和生活中出现的数学现象，而大数学家华罗庚也一针见血地分析过：“人们对数学产生枯燥无味、神秘难懂的印象，原因之一是数学教学脱离了实际.也许正是基于这些理念，国外的高中数学课程教材特别接地气，内容图文并茂，栩栩如生，涵盖了很多的生活场景，融入了很多国外的文化特色，充分体现了数学来源于生活的思想。

以下以加拿大11年级教材---预微积分（pre-calculas）和国内高中数学必修4的教材做简要比较分析。[3]

1.理论呈现和应用（以三角函数求值为例）

（1）教材内容展示

国内必修4数学教材（原文片段）：三角函数求值（诱导公式）

思考：我们利用单位圆定义了三角函数，而圆具有很好的对称性。能否利用圆的这种对称性来研究三角函数的性质呢？例如，能否从单位圆关于x轴、y轴、直线y=x的轴对称性以及关于原点O的中心对称性等出发，获得一些三角函数的性质呢？

探究：给定一个角α

（1）角π-α、π+α的终边与角α的终边有什么关系？它们的三角函数之间有什么关系？

（2）角-α的终边与角α的终边有什么关系？它们的三角函数之间有什么关系？

（3）角-α的终边与α有什么关系？它们的三角函数之间有什么关系？

……

设任意角α的终边与单位圆的交点坐标为P1（x，y）。由于角π+α的终边与角α的终边关于原点对称，角π+α的终边与单位圆的交点P2与点P1关于原点O对称，因此点P2的坐标是（-x，-y）。由三角函数的定义得

Sinα=y， cosα=x， tanα=；

sin（π+α）=-y， cos（π+α）=-x， tan（π+α）=

从而得公式二

……

我们可以用下面一段话来概括公式一～四：

α+k·2π（k∈Z），-α，π±α的三角函数值，等于α的同名函数值，前面加上一个把α看成锐角时原函数值的符号。

……

加拿大11年级数学教材（片段节选）

Pre-calculus 11： Trigonometric Ratios of Any Angle（三角函數值）

The Athabasca Oil Sands are located 40 km north of Fort McMurray， AB. They are the worlds largest source of synthetic crude from oil sands， and the greatest single source in Canada. （阿沙巴斯克油砂位于麦克默里堡北部40千米，他是世界上最大的合成原料来源，也是加拿大最丰富的能源）。Massive machinery has been developed specifically for the excavation of the oil sands. Power shovels are equipped with a global positioning system （GPS） to make digging more exact. The operator must understand the angles necessary to operate the massive shovel. The design of power shovels uses the laws of trigonometry.（特制的大型的机械设备如安装了GPS的挖掘机可以更准确的挖掘油砂， 它的设计运用了三角函数的知识，操作者需要懂得操作角度。）[4]

Hint： Reference angle（参考角的定义）

· the acute angle whose vertex is the origin and whose arms are the terminal arm of the angle and the x-axis（参考角即角的终边与x轴形成的锐角）

Signs of trigonometric ratios in the four quadrants.

（三角函数值在四个象限的符号）

The length of the line OA is unit.endprint

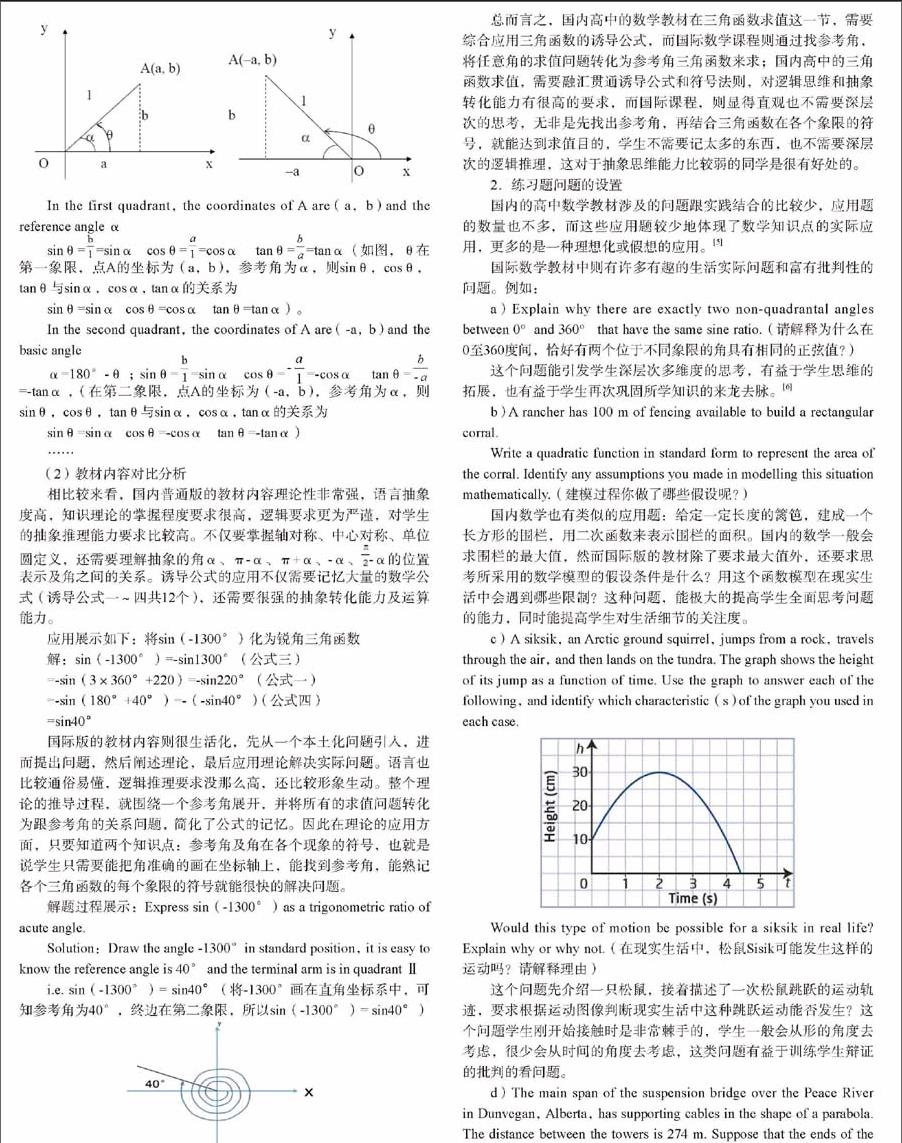
In the first quadrant， the coordinates of A are （a，b） and the reference angle α

sinθ==sinα cosθ==cosα tanθ==tanα （如图，θ在第一象限，点A的坐标为（a，b），参考角为α，则sinθ，cosθ，tanθ与sinα，cosα， tanα的关系为

sinθ=sinα cosθ=cosα tanθ=tanα） 。

In the second quadrant， the coordinates of A are （-a， b） and the basic angle

α=180°-θ ； sinθ==sinα cosθ==-cosα tanθ==-tanα ，（在第二象限，点A的坐标为（-a，b），参考角为α，则sinθ，cosθ，tanθ与sinα，cosα， tanα的关系为

sinθ=sinα cosθ=-cosα tanθ=-tanα）

……

（2）教材内容对比分析

相比较来看，国内普通版的教材内容理论性非常强，语言抽象度高，知识理论的掌握程度要求很高，逻辑要求更为严谨，对学生的抽象推理能力要求比较高。不仅要掌握轴对称、中心对称、单位圆定义，还需要理解抽象的角α、π-α、π+α、-α、-α的位置表示及角之间的关系。诱导公式的应用不仅需要记忆大量的数学公式（诱导公式一～四共12个），还需要很强的抽象转化能力及运算能力。

应用展示如下：将sin（-1300°）化为锐角三角函数

解：sin（-1300°）=-sin1300°（公式三）

=-sin（3×360?+220）=-sin220?（公式一）

=-sin（180?+40?）=-（-sin40?）（公式四）

=sin40?

国际版的教材内容则很生活化，先从一个本土化问题引入，进而提出问题，然后阐述理论，最后应用理论解决实际问题。语言也比较通俗易懂，逻辑推理要求没那么高，还比较形象生动。整个理论的推导过程，就围绕一个参考角展开，并将所有的求值问题转化为跟参考角的关系问题， 简化了公式的记忆。因此在理论的应用方面，只要知道两个知识点：参考角及角在各个现象的符号，也就是说学生只需要能把角准确的画在坐标轴上，能找到参考角，能熟记各个三角函数的每个象限的符号就能很快的解决问题。

解题过程展示：Express sin（-1300°）as a trigonometric ratio of acute angle.

Solution：Draw the angle -1300°in standard position， it is easy to know the reference angle is 40° and the terminal arm is in quadrant Ⅱ

i.e. sin（-1300°）= sin40?（将-1300°画在直角坐标系中，可知参考角为40°，终边在第二象限，所以sin（-1300°）= sin40?）

总而言之，国内高中的数学教材在三角函数求值这一节，需要综合应用三角函数的诱导公式，而国际数学课程则通过找参考角，将任意角的求值问题转化为参考角三角函数来求；国内高中的三角函数求值，需要融汇贯通诱导公式和符号法则，对逻辑思维和抽象转化能力有很高的要求，而国际课程，则显得直观也不需要深层次的思考，无非是先找出参考角，再结合三角函数在各个象限的符号，就能达到求值目的，学生不需要记太多的东西，也不需要深层次的逻辑推理，这对于抽象思维能力比较弱的同学是很有好处的。

2.练习题问题的设置

国内的高中数学教材涉及的问题跟实践结合的比较少，应用题的数量也不多，而这些应用题较少地体现了数学知识点的实际应用，更多的是一种理想化或假想的应用。[5]

国际数学教材中则有许多有趣的生活实际问题和富有批判性的问题。例如：

a）Explain why there are exactly two non-quadrantal angles between 0°and 360° that have the same sine ratio.（请解释为什么在0至360度间，恰好有两个位于不同象限的角具有相同的正弦值？）

这个问题能引发学生深层次多维度的思考，有益于学生思维的拓展，也有益于学生再次巩固所学知识的来龙去脉。[6]

b） A rancher has 100 m of fencing available to build a rectangular corral.

Write a quadratic function in standard form to represent the area of the corral. Identify any assumptions you made in modelling this situation mathematically.（建模过程你做了哪些假设呢？）

国内数学也有类似的应用题：给定一定长度的篱笆，建成一个长方形的围栏，用二次函数来表示围栏的面积。国内的数学一般会求围栏的最大值，然而国际版的教材除了要求最大值外，還要求思考所采用的数学模型的假设条件是什么？用这个函数模型在现实生活中会遇到哪些限制？这种问题，能极大的提高学生全面思考问题的能力，同时能提高学生对生活细节的关注度。

c）A siksik， an Arctic ground squirrel， jumps from a rock， travels through the air， and then lands on the tundra. The graph shows the height of its jump as a function of time. Use the graph to answer each of the following， and identify which characteristic（s） of the graph you used in each case.

Would this type of motion be possible for a siksik in real life？ Explain why or why not.（在现实生活中，松鼠Sisik可能发生这样的运动吗？请解释理由）

这个问题先介绍一只松鼠，接着描述了一次松鼠跳跃的运动轨迹，要求根据运动图像判断现实生活中这种跳跃运动能否发生？这个问题学生刚开始接触时是非常棘手的，学生一般会从形的角度去考虑，很少会从时间的角度去考虑，这类问题有益于训练学生辩证的批判的看问题。endprint