例谈中考数学几何压轴题的命制方法及创新设计

尚凡青+魏相清

[摘 要]从近几年中考数学试题的命题实践出发，总结了中考数学几何压轴题的命制方法及创新设计思路。在命制方法方面，主要介绍了几何压轴题的命题程序；在创新设计思路方面，着重介绍了基于几何压轴题的设计思路的创新考查。

[关键词]中考数学；命制方法；创新设计

新课改以来，中考数学试卷最明显的特点就是加大了对几何压轴题的考查力度，尤其是对探究性几何题的考查力度。几何压轴题的内容丰富，区分度大，涉及知识面广，已逐渐成为中考数学试卷的重点题型。综观近几年全国各地的中考数学试卷，大家都把几何题作为中考的经典题和压轴题，对探究性几何题的考查无论是考查内容还是考查形式都有所创新，体现了中考数学学科命题思路的灵活性、考查视角的新颖性和考查方式的多样性。几何压轴题能较好的考查学生的数学核心素养和理性精神，体现以素养立意的命题指导思想。在此，笔者以山东省东营市中考数学几何压轴题的命制为例，谈一谈对几何压轴题的命制方法及创新设计，以期对中考数学几何压轴题的命制及备考提供借鉴。

一、几何压轴题的命制方法

在中考数学试卷中，由于几何压轴题的分值较高，而且涉及的考点其他题目都容易回避，所以首先命制几何压轴题。通过对中考数学试题的研究发现，几何压轴题虽然没有固定的命题方法，但仍遵循一定的命题思路，我们一般按照“选题—改造—变式”的程序进行。

1.利用到各学校视导听课过程，收集一些比较经典的题目，然后进行创编。

在一次某学校的听课过程中，有位教师讲了这样一道比较经典的题目，引起笔者的注意，当时收集起来，最终经过创编形成了2017年东营市中考数学几何压轴题，题目如下：

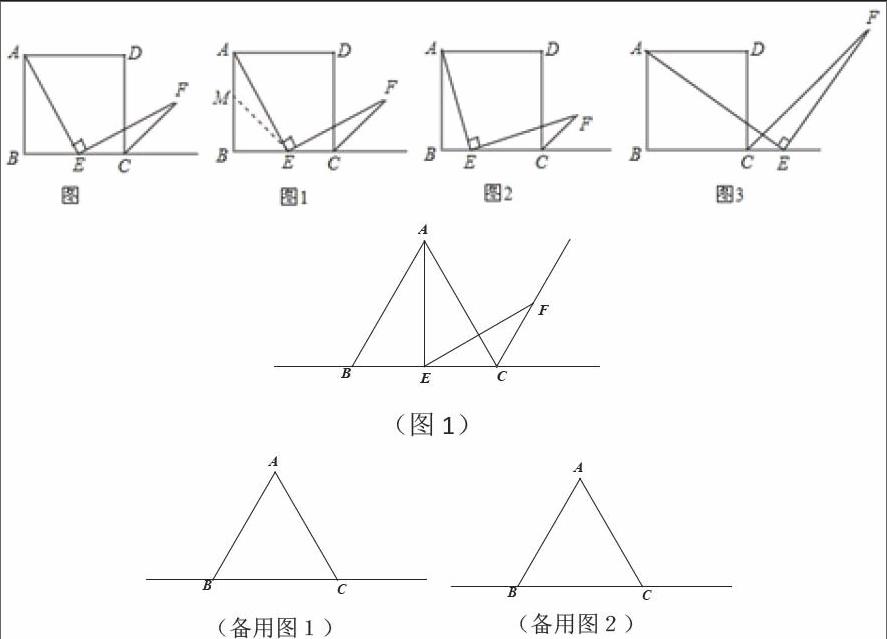
如图，在△ABC中，AB=AC=1，点D、E在直线BC上运动.点D在线段BC的左侧，点E在线段BC的右侧. 设BD =x，CE = y.

（1）如果∠BAC = 30°，∠DAE = 105°，试确定y与x之间的函数关系式；

（2）如果∠BAC的度数为α，∠DAE的度数为β，当α，β满足怎样的关系式时，（1）中y与x之间的函数关系式还成立，试说明理由.

由于此题目比较经典，命题组经过思考编制了如下的2017年东营市中考数学的几何压轴题第一稿，题目如下：

如图，在△ABC中，∠BAC=90°，AB=AC=1，点D是BC边上的一个动点（不与B、C重合），在AC上取一点E，使∠ADE=45°.

（1）求证：△ABD∽△DCE；

（2）设BD=x，AE=y，求y关于x的函数关系式及自变量x的取值范围；

（3）当△ADE是等腰三角形时，求AE的長.

后来，由于考虑到等腰直角三角形有点特殊，于是继续修改，便形成了2017年东营市中考数学的几何压轴题最终稿，题目如下：

如图，在△ABC中，∠BAC=120°， AB=AC=2，点D是BC边上的一个动点（不与B、C重合），在AC上取一点E，使∠ADE=30°.

（1）求证：△ABD∽△DCE；

（2）设BD=x，AE=y，求y关于x的函数关系式及自变量x的取值范围.

（3）设当△ADE是等腰三角形时，求AE的长.

2.利用各地的模拟题、中考题为原题进行创编

几何压轴题的命制有时通过对原中考题或模拟题进行的改造，2016年东营市中考数学几何压轴题便是对一道模拟题进行的改造并最终成稿的，原题如下：

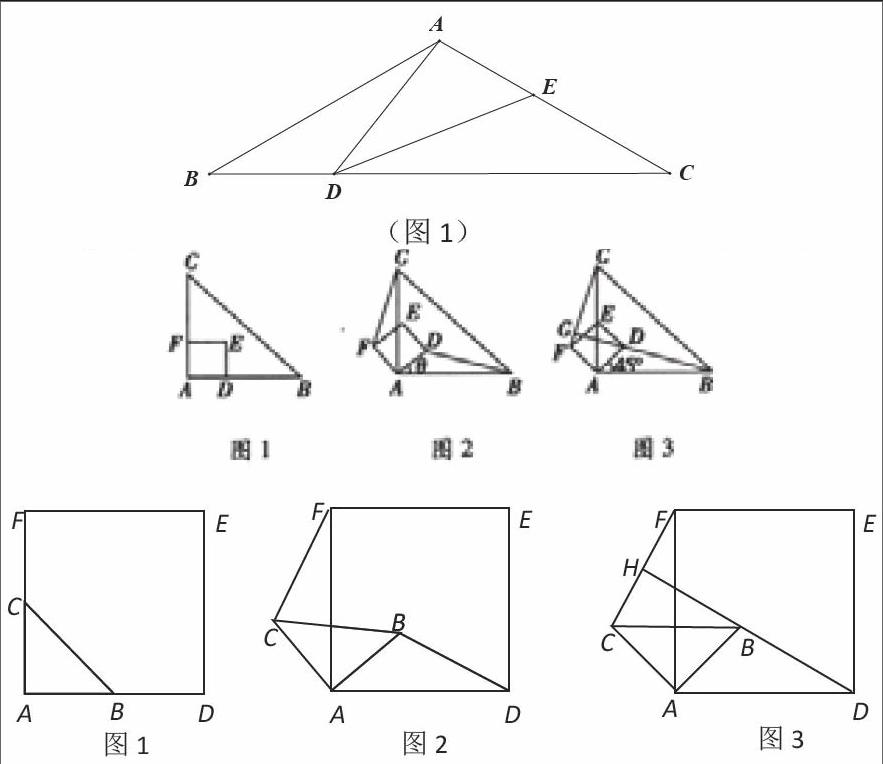
如图l，△ABC是等腰直角三角形，∠BAC=90°，AB=AC，四边形ADEF是正方形，点D、F分别在A B、AC边上，此时BD=CF，BD⊥CF成立.

（1）当正方形ADEF绕点A逆时针旋转θ （0°<θ<90°）时，如图2，BD=CF成立吗？若成立，请证明；若不成立，请说明理由.

（2）当正方形ADEF绕点A逆时针旋转45°时，如图3，延长BD交CF于点G.

①求证：BD⊥CF；②当AB=4，AD= 时，求线段BG的长.

经过对题目仔细研究发现，如果对图形进行适当的改变，如原图中“三角形大、正方形小”，换成“正方形大、三角形小”结论是否仍然成立呢？命题人员利用几何画板验证，结论仍然成立。此题具有改造的空间，于是便形成了2016年东营市中考数学几何压轴题，题目如下：

如图l，△ABC是等腰直角三角形，∠BAC=90°，AB=AC，四边形ADEF是正方形，点B、C分别在边AD、AF上，此时BD=CF，BD⊥CF成立.

（1）当△ABC绕点A逆时针旋转θ （0°< θ <90°）时，如图2，BD=CF成立吗？若成立，请证明；若不成立，请说明理由.

（2）当△ABC绕点A逆时针旋转45°时，如图3，延长DB交CF于点H.

①求证：BD⊥CF；②当AB=2，AD=3 时，求线段DH的长.

二、中考数学几何压轴题的创新设计

逻辑推理是学生发展所需的重要的数学核心素养，回想2014年中考数学几何压轴题的命制，当时设想是：改变前几年的旧习，结合初中数学四维目标的设定，以纯几何探究为主，适当强化几何推理能力的考查。由于压轴题一般要求：“起点低，入手易，逐渐增加坡度，区达到区分度大”，使基础知识好、数学素养好的学生能脱颖而出。为此，2014年东营市中考数学几何压轴题的命制是以课本练习题目为原型进行的创新设计。

原始模型（人民教育出版社义务教育教科书八年级下册P69页第14题）：

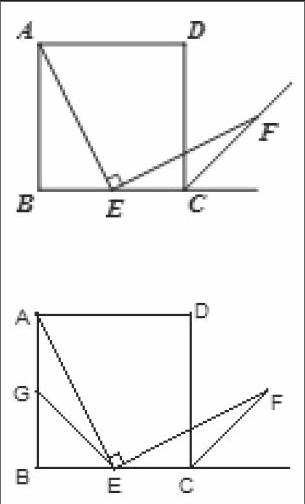
如图，四边形ABCD是正方形，点E是边BC的中点，∠AEF=90°，且EF交正方形外角的平分线于点F，求证AE=EF.（提示：取AB的中点G，连接EG.）

思考1：能否通过旋转不变性，同时结合考查学生的作图能力进行创编题目？于是便有了下面的第一稿：

如图，四边形ABCD是正方形，点E是边BC的中点且∠AEF=90°，且EF交正方形外角平分线CF于点F，取边AB的中点G，连接EG.

（1）求证：EG=CF；

（2）将△ECF绕点E逆时针旋转90°，问旋转后CF与EG是什么位置关系，请进行证明， 并在图中画出旋转后的图形.

上面的第一稿题目虽然满足预设，但是略显简单。

思考2：由于点E是边BC的中点，具有特殊性，能否通過对点E的位置变化进行创编题目？于是便有了下面的第二稿：

如图，四边形ABCD是正方形，点E是边BC的中点，∠AEF=90°，且EF交正方形外角平分线CF于点F.请你认真阅读下面关于这个图的探究片段，完成所提出的问题.

（1）探究1：小强看到图1后，很快发现AE=EF，这需要证明AE和EF所在的两个三角形全等，但△ABE和△ECF显然不全等（一个是直角三角形，一个是钝角三角形），考虑到点E是边BC的中点，因此可以选取AB的中点M，连接EM后尝试去证△AEM≌EFC就行了，随即小强写出了如下的证明过程：

证明：如图1，取AB的中点M，连接EM.

∵∠AEF=90°，

∴∠FEC+∠AEB=90°，

又∵∠EAM+∠AEB=90°，

∴∠EAM=∠FEC.

∵点E，M分别为正方形的边BC和AB的中点，

∴AM=EC，

又可知△BME是等腰直角三角形，

∴∠AME=135°.

又∵CF是正方形外角的平分线，

∴∠ECF=135°，

∴△AEM≌△EFC（ASA），

∴AE=EF.

（2）探究2：小强继续探索，如图2，若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”，其余条件不变，发现AE=EF仍然成立，请你证明这一结论.

（3）探究3：小强进一步还想试试，如图3，若把条件“点E是边BC的中点”改为“点E是边BC延长线上的一点”，其余条件仍不变，那么结论AE=EF是否成立呢？若成立请你完成证明过程给小强看，若不成立请你说明理由.

上面的创编题目，考查了特殊到一般的数学思想，同时还让学生进行应用，已经起到了很好的创新效果，但是学生的做题能力没有得到考查。

思考：正方形具有这样的性质，换一种图形，如正三角形是否仍然满足上述性质呢？通过几何画板进行度量验证，仍然成立，于是便创编生成了2014年东营市中考数学几何压轴题，题目如下：

【探究发现】如图1，△ABC是等边三角形， ，EF交等边三角形外角平分线CF所在的直线于点F.当点E是BC的中点时，有AE=EF成立；

【数学思考】某数学兴趣小组在探究AE、EF的关系时，运用“从特殊到一般”的数学思想，通过验证得出如下结论：当点E是直线BC上（B、C除外）任意一点时（其它条件不变），结论AE=EF仍然成立.

假如你是该兴趣小组中的一员，请你从“点E是线段BC上的任意一点”；“点E是线段BC延长线上的任意一点”；“点E是线段BC反向延长线上的任意一点”三种情况中，任选一种情况，在备用图1中画出图形，并进行证明.

【拓展应用】当点E在线段BC的延长线上时，若CE = BC，在备用图2中画出图形，并运用上述结论求出的值.

上面的题目是以教材练习题目为原型进行的创新设计，既考查了三角形全等的知识也考查了三角形相似的知识，同时考查了学生的作图能力，考察面较广。整个题目的创编过程富有创新性。可以说，此题是2014年东营市中考数学试题中一道亮丽的风景线！

三、命制几何压轴题的注意事项

命制一道高质量的几何压轴题难就难在它的创新性和开放性。创新性可以提高题目的新颖性，开放性能有效开阔学生的思维，通过问题让学生多思少写。因此要命制一道好的几何压轴题还必须注意以下几点。

1.应加大对学生核心素养的考查力度

中考几何压轴题应加大对学生核心素养的考查力度，注意学科的内在联系和知识的综合，因地制宜地编制一些针对性强、适合学生学习训练的数学问题，或者精选一些比较成功的几何压轴题，有目的的将它们进行组合或改编，有意识的培养学生的核心素养。

2.加强对中考试题的研究

中考几何压轴题常出常新，每年都有新题出现。因此，收集整理全国各地的中考数学试题，了解各地中考几何压轴题的命题趋势，从中寻找灵感，筛选出有亮点的新题，尤其是在变化过程中寻找不变性，并进行仔细研究，通过不变的性质，将陌生的问题转化为熟悉的问题，进而创编出高质量的几何压轴题。

3.注重对命题素材的积累

素材积累的越多，命题选择的余地就越大，命题思路就越开阔，试题的新颖度就越高。因此，我们要认真研读《中学数学教学参考》等杂志，注重收集整理其中有价值的新信息、新素材、新题型，及时做好命题素材积累。

4.命制的几何压轴题要渗透数学思想方法

要想使学生“做一题，会一类”，命制的几何压轴题要渗透数学思想方法，如数形结合思想，通过直观的图形变换揭示不同图形间的共性，进而运用化归思想进行转化，从而获得化归的切入点，做到举一反三，融会贯通。

随着中考命题改革的不断深化，几何压轴题的命制思路也会更加灵活，如何对几何压轴题进行创新设计，已经引起越来越多的命题人员的重视，几何压轴题设计的技巧和方法也不断得到发展和完善，也期待有更多构思巧妙、设计新颖的好题呈献给广大师生。

参考文献：

[1] 张建跃. 数学学习与智慧发展[J]. 中学数学教学参考：中旬，2015（7）：4-10.

[2] 魏相清. 对两道高考模拟题的解法反思[J].中学数学教学参考，2015（11）：33-35.