浅谈试题编制中“认识封闭”现象及其应对策略

■卞书彦

浅谈试题编制中“认识封闭”现象及其应对策略

■卞书彦

“认识封闭”是数学学习与研究中的常见现象，本文拟通过教材一道错题产生原因的剖析，谈谈题目编制中的“认识封闭”现象及其矫正策略。

一、问题提出

1.题目呈现

如图，△ABC的周长为24，面积为48，求它的内切圆的半径。

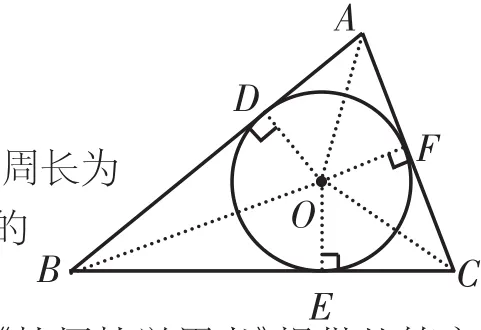
与教材配套的《教师教学用书》提供的答案是：设△ABC的内切圆的半径为r，切点分别为D、E、F，连接OD、OE、OF、OA、OB、OC。由题意，得OD⊥AB，OE⊥BC，OF⊥CA，且OD=OE=OF=r。

2.题目证伪

上述解答正确吗？我们知道，周长一定的三角形中，等边三角形的面积最大。不妨将问题特殊化：设AB=BC=CA=8，此时△ABC的面积最大为163〈16×3=48，显然“周长为24，面积为48”的三角形不存在。为进一步探究其周长与面积的关系，现将问题一般化：设三角形的三边长分别为a、b、c，面积为S，记(a+b+c)。

二、问题探因

该题旨在让学生通过问题解决，理解三角形的周长C、面积S、内切圆半径r的关系，即S=Cr，并知道已知其中两个量，可求第三个量，进而巩固三角形内切圆的相关性质。问题是：题目编写者只注重了三者之间形式化的关系，而忽视了隐含条件，根本原因就是“认识封闭”现象。

“认识封闭”是特有的思维错误现象，产生这一现象的原因较多，如数学知识结构不完整，数学思维方式与习惯偏差等。在题目编制中的“认识封闭”现象主要原因则是关联思维不够，缺乏高观点下理解数学问题的意识。

三、应对策略

应对题目编制中的“认识封闭”现象的策略较多，其中，优化思维方式、高观点解释问题是主要策略。

1.优化思维方式。一是提高关联思维的能力。无论是教师、还是教材编写者，并不缺乏数学知识，之所以出现认识封闭现象，主要还是缺乏对知识的系统整合与有效关联，形成思维定势，没有将题目数据与图形存在的条件整体地、关联地思考。因此，要在完善知识结构的前提下，注意提高自身整体地、关联地思维的能力，尽可能在题目编制中考虑与之相关联的知识、方法，并尝试从不同角度理解与解释。二是强化反思思维的意识。反思是一种重要的思维习惯，是思维深刻性与缜密性的具体体现。如果题目编写者对问题稍作反思，比如将问题特殊化或一般化，就不难发现题目的瑕疵。有时需要对问题条件进行探究，通过限定条件的外延与内含，使问题的结论具有确定性、可靠性。

2.高观点解释问题。数学的知识和方法是发展的，一般来说，上位（更高级）的数学知识和方法对下位（初级）的内容是兼容的，用上位的数学知识与方法可以更全面、更深刻地理解、解释下位的数学现象。因此，作为题目编制者，必须有这种意识，就是在编制题目时，用上位的数学知识、方法对题目进行验证，用高观点来看待编制的数学问题，只有居高临下，才能确保问题准确无误。

（作者为江苏省盐城市葛武初级中学校长）