浅析博弈论在财务评标过程中的运用
2017-08-16叶玉倩
叶玉倩
(安徽大学 安徽 合肥 230601)
浅析博弈论在财务评标过程中的运用
叶玉倩
(安徽大学 安徽 合肥 230601)
本文通过在不完全信息条件下的工程投招标模块引入贝叶斯纳什均衡等相关博弈理论,通过对企业财务报表中资本结构、偿债能力、获利能力等财务指标的评价,从数学概率角度对投标方和招标方的博弈进行量化测算,最终向双方提出一系列意见与建议,得出相应结论。
博弈论;财务评标;纳什均衡
一、背景概述
工程项目招标是招标人通过一定的程序,择优为其项目选择承包人的有效手段。招工投标的整个过程,各竞标人的根本利益是互斥的,投标方与招标方的得利是冲突的,竞标与招标行为相互影响,因此该过程实则为诸位投标人以及投标与招标双方之间的博弈过程,这是一种典型的博弈特征的竞争性活动,每一位投标人在进行投标报价决策时,必须考虑对手和招标方的反应,这便使得招标投标活动充满了博弈特征。因此各投标方需要积极判断和预测投资项目的投资回报率等财务指标,招标方的财务人员也需慎重考量和论证投标方的筹资成本、资金结构等财务信息。各市场参与方将在市场许可的条件下合法竞争,通过采取低成本、低风险的融资或投资政策,以期获得最大收益。综上所述,在工程投招标环节中,共享博弈论的研究成果、分析博弈论在财务评标过程中的具体运用是十分必要的。
二、理论阐释
财务会计模块会时常研究到工程招标投标环节,该环节的前提假设是投标人均为“理性经济人”,即投标人不会采取低于成本价的投标方式,使得当投标人的投标价低于其他所有投标价时即中标。用Ai表示行为,ui表示得益,Ti表示博弈方i的策略类型空间,Pi表示i在自己的策略类型为Ti的前提下,其他博弈方的类型或类型组合Ti={t1,…,t(i-1),t(i+1),…,tn}出现的条件概率,则在工程投招标过程中n个参与者的标准式博弈可用G={A1,A2,…,An;T1,T2,…,Tn;P1,P2,…,Pn;u1,u2,…,un}来表示。如果战略组合{A1*,A2*,…,An*}满足对每一参与者i,Ai*是(至少不劣于)他针对n-1个参与者所选战略{A1*,A2*,… ,A(i-1)*,A(i+1)*,…,An*}的最优反应战略,则称战略组合{A1*,A2*,……,An*}是该博弈的一个纳什均衡,即ui(A1*,A2*,…,A(i-1)*,Ai*,A(i+1)*,…,An*)>ui(A1*,A2*,…,A(i-1)*,Ai,A(i+1)*,…,An*)对所有Ai都成立。下面我们将着重对企业财务评标过程中运用的博弈理论进行分析。
三、博弈论在财务评标过程中的具体运用
投标过程中,竞标者需要测算投入该项目的自有资本获取净收益的能力,净资产收益率可综合反映投标人投入资本与其累积获取的报酬之间的联系,而盈余现金保障倍数(经营现金净流量/净利润)也可综合反映投资项目的盈余质量。由于每位投标人仅知晓个别成本,即自己对工程的估价,并不知道除私人信息外的其他人的工程估价,即使涉及也只是对其有个大概范围了解,因此信息不完全;另外投标人之间是独立做出各自的决定,故是静态的。综合来看,工程项目招投标属于典型的不完全信息静态博弈。每位投标人根据自己对工程估价和其他人的大致估价来判断并作出策略,由此可得,投标人为取得有竞争力的投标价,需要同时保证该投标价的中标概率最大,且该投标价中标能够获得一定利润,另一不可忽视的保证是在满足工程的质量、进度等要求下,招标人能够接受此投标价。
我们由前述引申得出以下定义:静态贝叶斯博弈G={A1,…,An;T1,…,Tn;P1,…,Pn;u1,…,un}中,如果对任意博弈方i和他的每一种可能的类型ti∈Ti,Si(ti)所选择的行动Ai都能满足:
则称策略组合S=(S1,…,Sn)为G的一个纯策略贝叶斯纳什均衡。在工程招投标模块,海萨尼转换通过引进虚拟的自然博弈方0,让每个博弈方知道自己的类型,但不让全部或部分博弈方知道其他博弈方的类型,以此将不完全信息静态博弈转化为不完美信息动态博弈。然而实际招投标过程中,由于提供的信息量少,所以财务人员在评标过程中应充分利用已有信息。投标方可通过观察招标企业公布的收入、利润等业绩情况,再比对同行业企业的业绩资料,并同时解读标的项目的相关文件,测算其相对客观的市场占有率和自身实力,通过其提供的标的项目的资料,判断披露的财务和经营信息是否前后一致,若回避问题,则应扣除相应的项目评估分值。
我们现描述模型如下:假定仅有两个投标人,博弈方1和博弈方2,他们对拍品的估价分别为V1和V2,V1与V2相互独立且均服从[0,1]的标准正态分布,博弈方i知道自己的估价和另一方估价的概率分布,且其行为即其标价bi,行为空间Ai=[0,1],则博弈方i的得益函数为:当bi>bj时,Ui=ui(b1,b2,v1,v2)=vi-bi;当bi=bj时,Ui=ui(b1,b2,v1,v2)= (vi-bi)/2;而当bi 综合以上,分别针对工程投标人和招标人获得最大收益的期望提出相应的策略意见与建议:一方面,理性的投标人应根据市场现状,运用科学的方法计算自己应得的利益,通过分析竞争对手的历史报价来预测竞争对手当前行为,进而保证能够较准确的估计竞争对手的报价,甚至可能分析并预测可能的中标价,编制高水平的投标书,力争以最低成本价竞标,还可以通过提高效率以降低成本,进而提高企业的“可降价空间”;另一方面,招标人在招标时,需要对投标人的资质和实力进行预审,包括考察投标人的业绩和信誉,以淘汰无法胜任工程要求的投标人,结合公开招标时采取的低价中标原则,这样既有利于招标人以一个较低的报价选择一个优秀的承包人,也有助于同时维护招标人和投标人双方共同的利益。 工程投招标过程中需要利用博弈理论进行合理测算和归纳总结,投标人的财务状况是招标机构衡量其履约能力的重要指标,而投标人履约能力的评估则需要用到博弈论的知识,纳什均衡相关理论也应用广泛。反之,投标人对项目收益和风险的评估也离不开博弈论理论。由本文可得出,投标人应尽可能降低工程造价,节约工程投资以提高工程效益,一旦中标,中标人须保证按时、按质、按量完成任务,促进健康稳定和谐发展的建筑市场的建立,促进整个建筑市场的良性发展,实现“共赢”。 [1]林楠.浅论财务人员在招标工作中的作用[J].中国乡镇企业会计,2010(8):97-98 [2]黄平.浅论财务人员在评标过程中的作用[J].财经界,2013(6):138-140 [3]刘康.基于博弈论的建筑工程投标报价最优化分析[J].工程管理学报,2015(6):124-128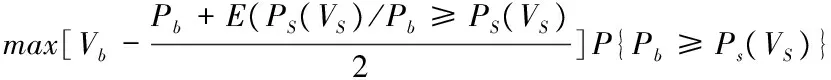
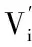
四、结论
