测量杨氏模量实验方法的探讨

王巍

（青海省产品质量监督检验所，青海西宁，810008）

测量杨氏模量实验方法的探讨

王巍

（青海省产品质量监督检验所，青海西宁，810008）

杨氏模量(Young’s modulus)是表征在弹性限度内物质材料抗拉或抗压的物理量，它是沿纵向的弹性模量。根据胡克定律，在物体的弹性限度内，应力与应变成正比，比值被称为材料的杨氏模量，它是表征材料性质的一个物理量，仅取决于材料本身的物理性质。

杨氏模量；悬丝耦合法

1 杨氏模量测量的基本介绍及发展展望

杨氏模量的大小标志了材料的刚性，杨氏模量越大，越不容易发生形变。杨氏弹性模量是选定机械零件材料的依据之一是工程技术设计中常用的参数。杨氏模量的测定对研究金属材料、光纤材料、半导体、纳米材料、聚合物、陶瓷、橡胶等各种材料的力学性质有着重要意义，还可用于机械零部件设计、生物力学、地质等领域。

目前测定物体材料的杨氏模量的方法很多，基本可分三类：（1）静态测量法；（2）动态测量法；（3）波速测量法。

大多数的研究机构做测定金属材料杨氏模量实验都采用静态拉伸法。采用这种方法，由于拉伸时载荷太大，加载速度慢，存有弛豫过程，不能真实地反映，材料内部结构的变化。对脆性材料(如玻璃、陶瓷等)无法用这种方法测量。也不能测量在不同温度时材料的杨氏模量 而弯曲共振法因其适用范围广(不同的材料和不同的温度)，实验结果稳定，误差小而成为世界各国广泛采用的测量方法(例如美国的标准号为ASTMC623-71，日本的标准号为JISAll27--1976)。

传统的杨氏模量测量方法中，钢丝的伸长量是利用光杠杆放大原理测量并求得的，这种方法存在着诸多问题。首先是实验的系统误差．操作时先要将仪器调节至标准状态，即负荷为零时，光杠杆镜面法线与望远镜光轴重合；标尺与光杠杆镜面相平行且铅垂于地面。设加上负荷后平面镜的偏转角度为θ。在标准情况下，求杨氏模量所用公式是通过θ近似等于tanθ得到的，由这种近似方法形成的相对实验误差为：

当θ较小时，此误差很小，但随θ增大此误差近似地以(2θ)的3次方倍增大。故当负荷很大时，该系统误差就不能忽略。

其次是望远镜光轴倾斜所产生的误差．假设当金属丝下端没有负荷时，望远镜光轴与水平面之间有一倾角θ，那么望远镜光轴倾斜对实验产生的相对误差公式为：

最后是光杠杆镜面倾斜所产生的误差．当钢丝下端没有负荷时，设望远镜光轴保持水平，光杠杆镜面与铅垂面之间有一夹角口，那么光杠杆倾斜对实验造成的相对误差公式为：

可见传统光杠杆和望远镜标尺组成的系统测量杨氏模量时，望远镜光轴倾斜或光杠杆镜面倾斜对测量结果影响都比较大。并且利用伸长法测杨氏模量时，光杠杆镜面与望远镜光轴都是通过手工调节，不可避免会存在误差。因此为了使测出的杨氏模量更准确，有必要对杨氏模量普通光杠杆法测量装置进行改进。

用悬丝耦合弯曲共振法测定金属材料杨氏模量的基本方法是：将一根截面均匀的试样(圆截面棒或矩形截面棒)用两根细丝悬挂在两只传感器(一只激振，一只拾振)下面，在试样两端自由的条件下，由激振信号通过激振传感器使试样做横向弯曲振动，并由拾振传感器检测出试样共振时的共振频率。再测出试样的几何尺寸、质量等参数，即可求得试样材料的杨氏模量。

根据理论推导经验公式可得圆形截面和矩形截面的公式分别如下：

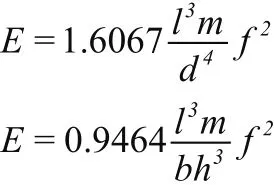
上式中l为试件长，d为圆形试件的直径，b和h分别为矩形试件的宽度和厚度，m为试件的质量，f为试样的共振频率。

图1 试样在作基频振动时，存在节点示图

值得注意的是，在推导以上两个公式时是根据最低级次(基频)对称形振动的波形导出的。图1中给出，试样在作基频振动时，存在两个节点，分别在0.2241和0.7761处。显然节点是不振动的，实验时悬丝不能吊扎在节点上。

根据原理，实验装置可作如图2安排。

图2 试验装置的机构图

在原理部分，已简单述及了试样作基频对称型振动时，存在两个节点，节点是不振动的，实验时悬丝不能吊扎在节点上，必须偏离节点。在原理中，同时又要求在试样两端自由的条件下，检测出共振频率，显然这两条要求是矛盾的。悬挂点偏离节点越远，可以检测到的共振信号越强，但试样受外力的作用也越大，由此产生的系统误差也越大。为了消除该误差，可采用内插测量法测出悬丝吊扎在试样节点上时，试样的共振频率。具体的测量方法可以逐步改变悬丝吊扎点的位置，逐点测出试样的共振频率f。

2 悬丝耦合法测量杨氏模量的应用与发展概况

2.1 普及情况与精度水平

悬丝耦合弯曲共振法被定为我国测量金属杆杨氏模量的标准方法，它亦被广泛用于轴向均匀、阻尼系数不大于10-3量级的各种凝聚态物质的杆状试样的性能检测。在满足上述规定(推荐)的技术条件下，检测精度可达1%量级，分辨率可达1‰量级。悬臂弯曲共振法主要用于丝、带材制成的小尺寸试样性能的检测，测量精度可达5%。在阻尼材料的性能检测中亦有应用。

2.2 优缺点分析与发展方向

如果能保证被悬置的试样处于自由振动状态，悬丝能被拉紧且换能器具有足够高的能量转换效率，则“悬丝耦合弯曲共振法”可作为检测径长比近于零的杆状试样动态杨氏模量的优选方法。在精密测量中，将遇到因试样的支撑点与能量耦合点合一而带来的强迫共振的影响问题，此时虽可用通过改变悬点来向振动节点逼近的方法予以排除，但操作较烦琐。悬臂弯曲共振法应用中的主要问题是试样实际振动长度的测量问题，由于难以满足具有足够刚性的试样在无塑性变形前提下的刚性夹持条件，实际检测结果多出现负的系统偏差。自动化是诸多测量方法的发展方向，在悬丝耦合法中能自动完成共振频率检测的工作原理是通过能量正反馈的方法使试样的固有振动达到可检测的程度从而完成频率测量工作。技术关键是采用锁相环技术来保证反馈信号的相位与试样固有振动信号相位间的一致。据报道，该方法对低内耗样品的共振频率测量精度可高于0.5%。

[1]潘人培主编.物理实验[M].南京:东南大学出版社，1993.3.

[2]李昕.弹性测量方法[J].金属材料研究，1975，3;1976，4(1).

[3]吴思诚．王祖铨主编[M]．近代物理实验．北京：北京大学出版杜，1995.7.

[4]李希陪.实验的数学处理[M].北京：科学出版社，1983.

[5]费业泰.误差理论与数据处理[M].北京：机械工业出版社，1989.

[6]何国伟.计量与测试分析方法[M].北京：国防工业出版社，1988.

[7]余祖俊.微机检测与控制应用系统设计[M].北京：北方交通大学，2001.

[8]张国忠.检测技术[M].北京：中国计量出版社，1998.

Discussion on the experimental method of measuring Young’s modulus

Wang Wei
(Qinghai Institute of product quality supervision and inspection, Qinghai Xining，810008)

Young’s modulus (Young’s, modulus) is a physical quantity that represents the tensile or compressive properties of a material in an elastic limit. It is the modulus of elasticity along the longitudinal direction. According to Hooke’s law, the objects within the elastic limit, stress is proportional to the ratio, known as the young’s modulus, it is a physical quantity to describe the material properties and physical properties depend only on the material itself.

Young’s modulus; suspension wire coupling method