基于高阶谱谱骨架的信号细微特征识别

王欢欢 张 涛

(解放军信息工程大学信息系统工程学院 河南 郑州 450000)



基于高阶谱谱骨架的信号细微特征识别

王欢欢 张 涛

(解放军信息工程大学信息系统工程学院 河南 郑州 450000)

为解决同型号辐射源识别问题，针对实际信号，采用信号的高阶谱作为个体识别的基本特征向量，建立基于软K段主曲线算法的高阶谱谱骨架模型。将谱骨架的信息维数和盒维数作为特征矢量，并结合信号的时频域分析。最后将得到的融合特征使用SVM分类器进行训练识别，实现对不同辐射源信号的个体识别。通过对比实验充分验证该方法的有效性。实验结果表明，在低信噪比的环境下，该方法能够有效地识别个体信号，具有更好的识别效果，识别率可达到85%以上。

高阶谱 主曲线 分形维数 识别率

0 引 言

通信辐射源信号细微特征分析是指在分析截获通信辐射源信号的基础上，得到信号中通信设备的个体特征。然后利用这些特征参数来获取该通信设备的工作状态、活动规律等信息[1]。目前该项技术取得了广泛的应用，在军事方面，通过对截获的信号进行个体识别分析，可以掌握敌方设备工作状态以及作战能力，在很大程度上能提升己方战斗力；在无线网络安全方面，利用该项技术对接入无线网络设备的硬件进行身份验证，在接入设备的物理层施加安全措施、验证连入的无线网络是否合法[2]，将会极大地提高无线网络的安全性能。另外该项技术在通信资源管理、机器人工智能、设备故诊断等领域也有很多实际的应用。

高阶统计量现在已成为信号处理的一种有力数学工具，以往的信号处理方法[3-5]中，常常是以二阶统计量(时域为相关函数、频域为功率谱)作为数学分析工具的，但是相关函数和功率谱存在一些缺点。例如它们具有等价性，不能辨识非最小相位系统；又比如，它们对加性噪声明显，一般只能处理加性白噪声的观测数据；而且从高阶谱中可以得到信号更多的信息，比如无法在功率谱中得到的相位等信息。为了克服这些缺点，就必须使用三阶或更高阶数的统计量进行处理。主曲线的基本思想就是在数据集中寻找一条光滑通过的曲线，使得曲线是数据集合的光滑线性平均，同时，数据点集合到曲线的正交距离最小。由于主曲线的自相合的特征和能够描述数据中心线的性质，在信号处理、图像和语音识别等多个领域有了广泛的应用[6-7]。Verbeek等[8]重新定义了软K段主曲线算法，通过分析原始数据的局部主成分从而得到k值，并根据数据的光滑性依次连接构成主曲线，这样能够较为真实地描述数据的真实形态。在文献[9]中，采用了利用信号的功率谱骨架信息作为基础特征向量，但是由于功率谱的局限性，包含的信息较少，这样能够表征辐射源的有用信息势必会减少，最终会带来识别结果的降低。本文在文献[9]的基础上采用了信号的高阶谱作为个体识别的基本特征向量，然后以软K段主曲线算法为基础、构建主曲线来提取信号高阶谱的骨架信息，最后采用分形方法进行骨架对比，并结合时频域分析建立了一种基于高阶谱谱骨架的特征提取方法，以达到个体识别的目的。提出了一种基于高阶谱谱骨架的特征提取方法，并通过实际信号的实验对比，验证了本文方法具有更好的效果以及更强的实用性。

1 基于高阶谱分析的基本特征提取

参与分类识别的特征需要具有时移不变性、尺度变化性、相位保持性等特点，而高阶谱就具有这样的特性。本文采用非参数化直接双谱对信号进行分析，之后计算双谱的矩形积分作为信号的基本特征。

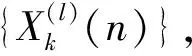
2) 计算信号的直接双谱：

(1)

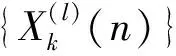
(2)

其中，Sl路径如图1所示。

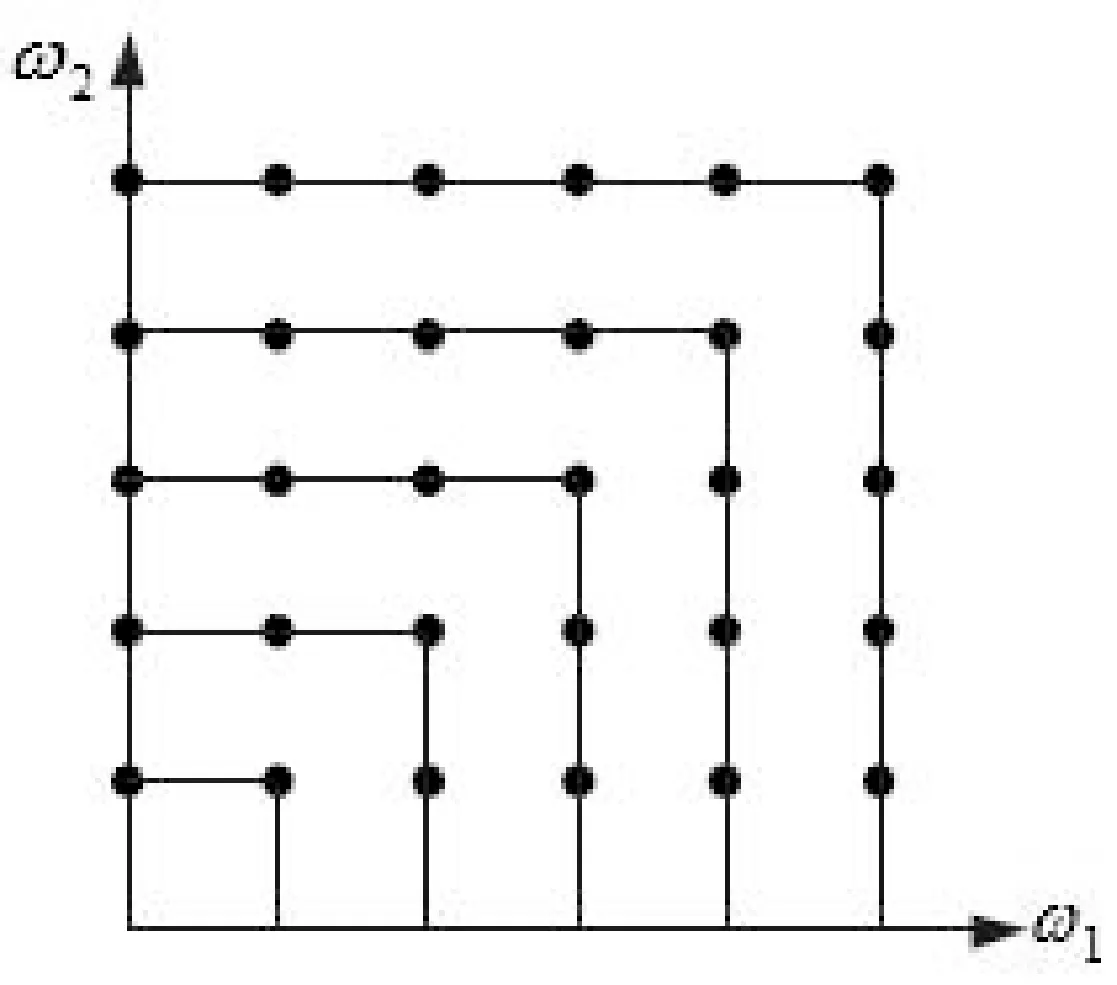
图1 矩形积分路径示意图

图2是两个辐射源的信号片段的双谱图，此双谱图是用等高线来定性刻画的，其目的只是为了方便观察不同辐射源信号高阶谱的差异。其中(a)、(b)为同一辐射源所发送信号的两个不同片段，(c)、(d)为另一辐射源所发送信号的两个不同片段。可以看出，不同辐射源的信号双谱明显不同，而同种辐射源的信号双谱具有某种自相似性，可以作为信号进行个体识别的基本特征向量。

图2 不同辐射源信号的双谱图

2 基于软K段主曲线谱骨架提取

在上文中，我们提取到信号的高阶谱后，往往会出现数据维数比较高而难以处理的情况，这时一般会采用线性主成分分析PCA等方法进行降维。但是在传统的多元数据分析中，对于数据集的分布一般是建立在统计意义上，而实际处理的信号则更多地会表现出高度非相关性和非线性结构等特点，因此需要把线性主成分分析向非线性进行推广。而主曲线就是这样的一种方法，它是使用光滑的曲线来代替主成分线来分析数据，求出对称变量之间的光滑曲线，是一种在基于线性的主成分分析方法的基础上、向更精确描述实际问题的非线性分析方法的延伸。文献[10]提出了主曲线的算法步骤，采用局部主成分构成k条线段，依据它们的光滑性来形成主曲线。

算法过程如下：

1) 初始化

(1) 读入数据点集X=(x1,x2,…,xn)。

(2) 计算其第一主成分线的方差为σ2，设初始线段s1长度为3σ，并设定k=1。

2) 插入一条新线段

(1) 在数据点集X中，计算点xq的Voronoi regions区域(VRs)为：

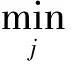
(3)

其中，d(x,sj)=‖x-xj‖2。

(2) 计算区域的第一主成分线，取其3σ长作为新插入线段,σ为第一主成分线的标准差。

(3) 令k=k+1，sk为新插入的线段，依照此过程进行迭代，直至新插入线段sk的Voronoi区域为Vk=Φ。

(4) 定义线段原来的VRs为V,如图3所示。

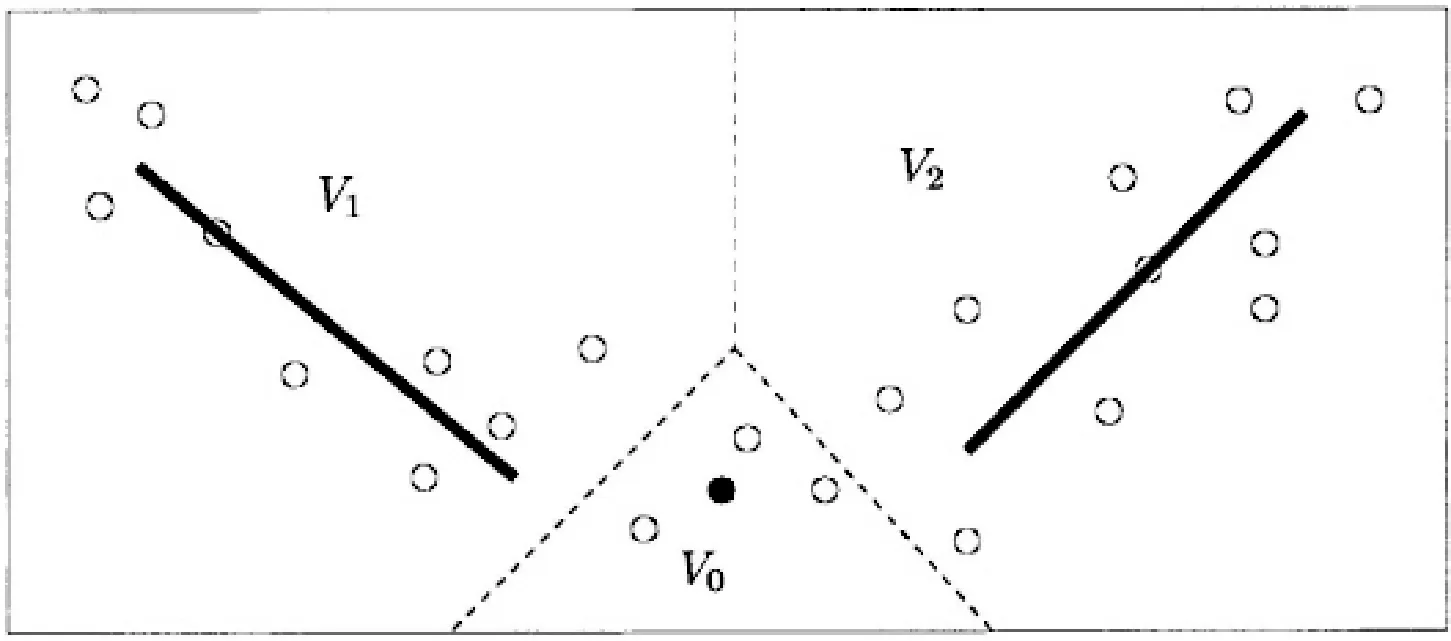
图3 数据点集合被划分为三个VRs

求出现在的每条线段新的VRs为V′,对比V′区域是否与V区域相同，若相同，继续步骤(2)，若不同，把V′区域赋给V区域。

3) 构造优化

将k条线段构造成一条哈密尔顿路径，并进行优化，算法如下：

(1) 令p=k，其中，p为路径的个数。

(2) 如果p<2,停止，否则求代价函数c(ei)=l(ei)+λ1α(ei)，ei=(vl,vm)，vl、vm分别是两个不同子哈密尔顿路径的端点,0≤λl∈R为自定义参数，l(ei)为ei的长度，l(ei)=‖vl-vm‖，如图4所示，α(ei)=α+β为角度惩罚，连接使c(ei)最小的边的端点，p=p-1，返回步骤(2)，继续进行迭代。

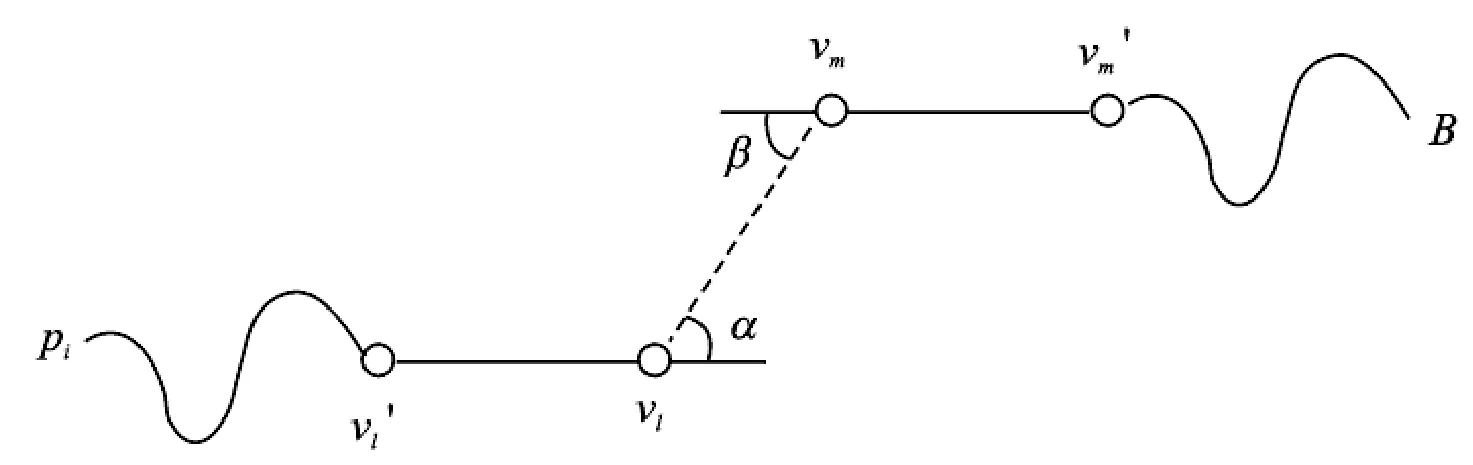
图4 子哈密尔顿路径角度惩罚图

(3) 计算目标函数

(4)

其中,n为数据点集X的数据个数，l为生成哈密尔顿路径的长度，σ2为第一主成分线的方差，如果此目标函数不是最小，返回步骤(2)继续运行。由以上步骤可获得主曲线。

软K段主曲线是提取信号谱骨架的有力工具，从以上算法可以得到不同样本片段的高阶谱谱骨架信息。从图5可以看出，不同信号片段提取出的谱骨架具有明显的差异，为下步的个体识别奠定了理论基础。

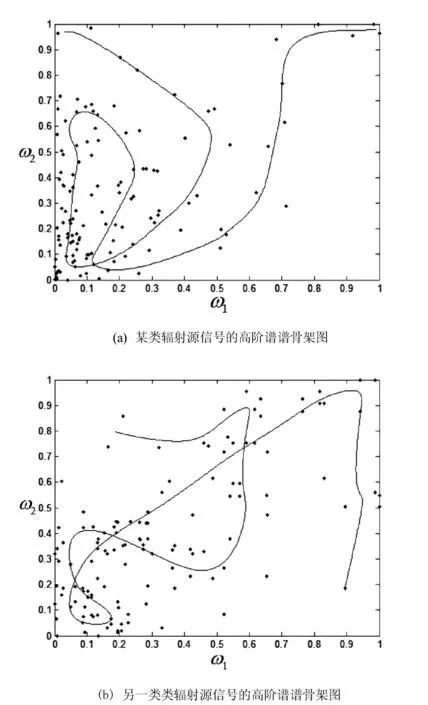
图5 不同信号的高阶谱谱骨架

3 谱骨架分形计算及特征融合

由于信号的高阶谱谱骨架是不规则的、非线性的、没有一定的规律进行比较，传统的方法无法直观地比较高阶谱谱骨架的差异，仍然无法对信号进行分类识别。文献[11]指出，分形是用于描述没有特征长度但整体上有一定自相似性的图形和结构，它具有精细结构和在统计意义下的某种自相似性。分形维数通过在一定程度上反映与体现整体系统的特性和信息来定量描述信号的变化特性。信号的高阶谱的谱骨架能反映出其几何形态，因此可以将信号高阶谱谱骨架的分形集的维数来作为个体信号的特征来进行个体识别。在分形维数中，盒维数和信息维数比较常用，同时抗噪性比较好，因此在本文中，采用信号高阶谱谱骨架的盒维数和信息维数作为个体信号的特征进行分类识别。

3.1 盒维数

盒维数是分形维数中比较常用的一种方法，它的大小可以反映出信号高阶谱谱骨架的复杂度，由于盒维数计算简单，从而得到了很广泛的应用[12]。可定义如下：

设集合F中的任意一个非空的子集为A，令N(F)表示为能够覆盖A的最小单位盒子，δ为盒子的边长，则F的盒维数dimbF可以定义为：

(5)

3.2 信息维数

信息维数的大小反映了集合F分布的疏密程度。设集合F落入边长为δ的第i个网格的概率为Pi，则其不确定性可以用信息熵来表示：

(6)

可定义信息维数为：

(7)

3.3 特征向量的融合

辐射源个体识别要求用于区分不同对象的属性集必须能够充分反映类别内各个对象最显著的特征。要解决同批次辐射源的个体识别问题，待分类对象的差异是用来识别的基础，这些差异一般会体现在通信信号上的时域、频域、时频域[13-14]或杂散特征等方面。因此针对特定的分类对象，在高阶谱谱骨架中融合与通信信号密切相关的参数，对提高识别率是很必要的[15]。对从不同角度提出的常规信号特征和谱骨架特征进行融合，并定义辐射源信号的特征标记为：

x={dimbF,DI(F),F(i),i=1,2,…,10}

(8)

其中，dimbF、DI(F)分别为盒维数和信息维数，根据文献[16]，可以得到十种时频域特征与其融合以提高识别结果，分别是在信号希尔伯特黄变换HHT(Hilbert-Huang transform)谱中得到的频域能量分布熵、频域能量分布的峰态、频域能量的偏移程度、频域能量的中心、时间能量分布熵、时间能量分布的峰态、时间能量的偏移程度、时间能量的中心、时频能量分布熵、时频能量中心十种特征。

4 分类识别

在20世纪90年代末，机器学习和模式识别领域迅速掀起了一个支持向量机研究和应用的热潮，与传统的模式识别方法以及人工神经网络方法相比，支持向量机的最主要特点是它能够在样本数相对较少、特征维数高的情况下仍然取得较好的推广能力，比较适合本文的实验数据的特点。本文针对的是数据集非线性可分的特点，利用支持向量机采用引入特征变换将原空间中的非线性问题转化成新空间中的线性问题。

假定有训练样本集：

(x1,y1),(x2,y2),…,(xN,yN)xi∈Rdyi∈{+1,-1}

(9)

其中，每个样本是d维向量，y是类别标号，ω1类用+1表示，ω2类用-1表示。在高维空间内求得最优超平面为：

(10)

其中，sgn()为符号函数，当自变量为正值时函数取值为1，自变量为负值时函数取值为-1。αi表示样本的拉格朗日中乘子，(xi·x)表示内积核，b表示固定的阈值。

但是，核函数需要针对具体问题来具体选择。在本文中，采用的是累积的方法来选择核函数参数，采用libSVM,按照规定的网格自动用各种参数取值来进行实验，根据每个参数取值下的留一法交叉验证结果来选择最佳的参数。

5 实验分析

本文采用某部实测调制方式相同的舰船信号作为本次辐射源个体识别实验的原信号，按信号可分为五种不同的辐射源。在此根据本文方法所提取的基于高阶谱谱骨架细微特征来进行识别。

实验信号的时域波形图如图6所示。

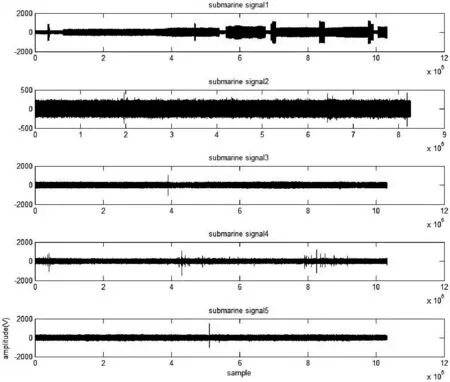
图6 实验信号的波形图

首先对所有信号进行预处理，去除信号中不包含调制信号的噪声部分。将每一类完整信号按照每N个数据点作为一个信号片段进行处理，在本文中设置N=512，设信号的长度为n，则可以得到n/N个连续的信号片段，训练样本和测试样本可以从中进行选取。在得到的n/N个信号片段中，为了避免个别信号片段同时用于训练和测试而由此带来的对实验结果的影响，在n/N个样本中，从奇数片段中随机选取500个信号片段作为训练样本，从偶数片段中随机选取200个信号片段作为测试样本。最终会从五类信号中得到2 500个训练样本和1 000个测试样本。对信号片段进行处理，求取信号片段的高阶谱谱骨架特征，通过SVM分类器的学习和识别统计出每类辐射源信号的识别率大小。识别率越大，表明对该信号识别得越准确。

图7是五种辐射源信号分形维数的二维特征分布图，其中横坐标为盒维数，纵坐标为信息维数，每类样本取500个训练片段。从图中可以看出，每种辐射源信号特征分布的收敛性较好，即同类辐射源发射出的信号的分形维数特征大部分都能够聚到一起，可以知道，同一辐射源的分形维数分布比较接近，因此本文中的特征提取方法是有效的。

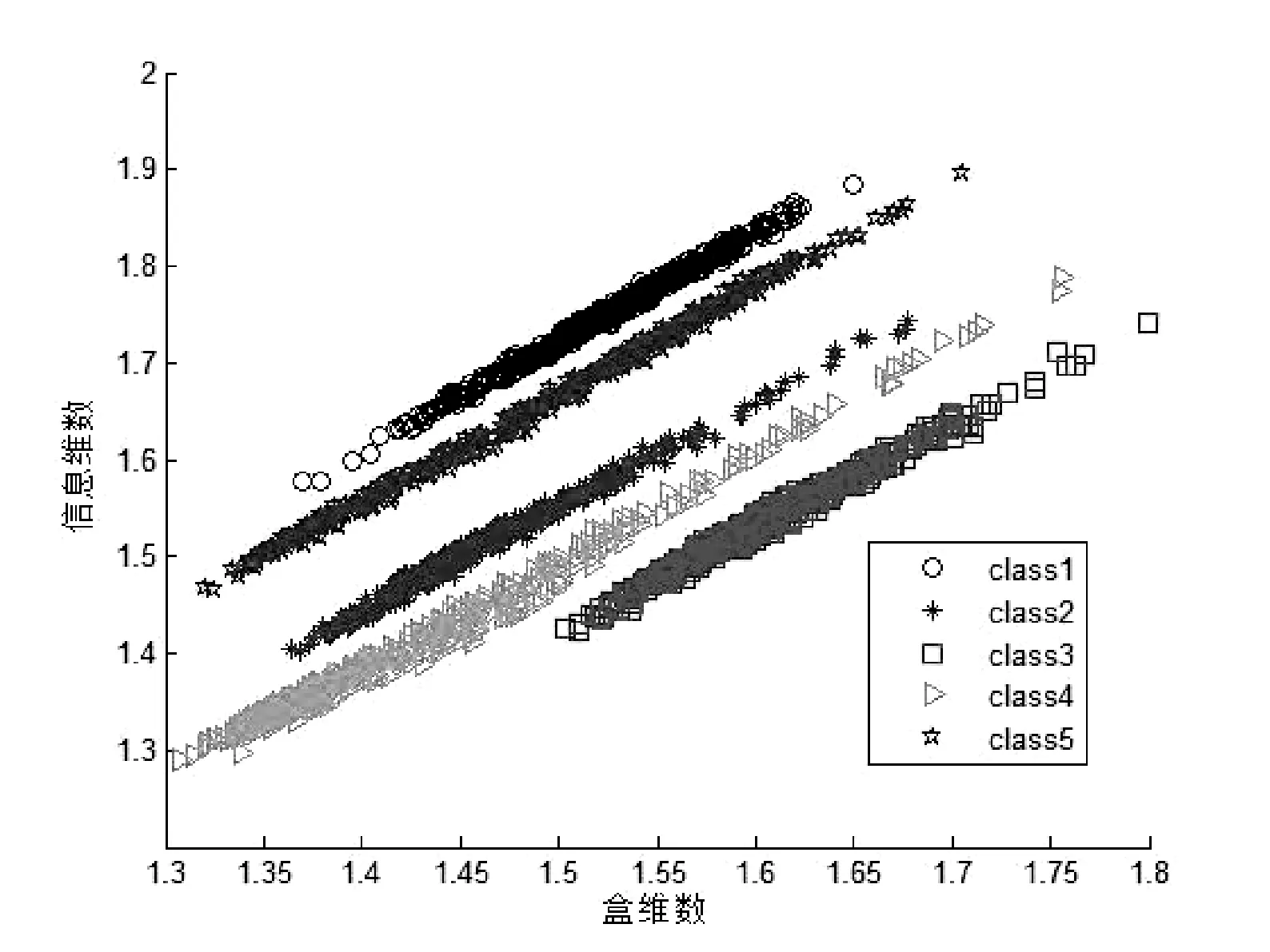
图7 分形维数二维特征分布

在本文中，特征提取算法采用的是在使用高阶谱谱骨架的基础上，结合文献[16]中的时频域分析方法提取出的十种时频特征进行分类识别。经以上步骤得到训练集和测试集后，设置核函数，设定分类器的惩罚参数c和核函数中的gamma参数g。为了得到最好的分类效果，通过交叉验证法找出使识别率最大的参数c和g,图8是用等高线表征的识别曲线图，表示识别率的值随着参数c和g的取值而不断发生变化，其最大识别率为90.1%。其中，横轴表示对分类器的惩罚参数c取对数，纵轴表示对核函数中的gamma参数g取对数,把log2c设定在[1,4]间，log2g设定在[-4,1]间，在此网格区间内进行交叉搜索。把训练标签和训练样本输入分类器进行训练，求得每两类的支撑向量和超平面。

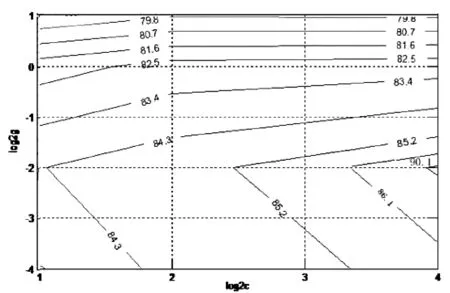
图8 参数c和g取不同值时对应的识别率

表1为五种辐射源信号的识别结果，本结果是随机选取每个辐射源信号200个测试片段进行投票判别取得的识别结果。从表中可以看到，每种辐射源的信号类别基本都能够识别出来，因此，本实验表明了信号高阶谱的谱骨架能够反映辐射源信号数据集的内在结构，可以作为信号识别的细微特征。

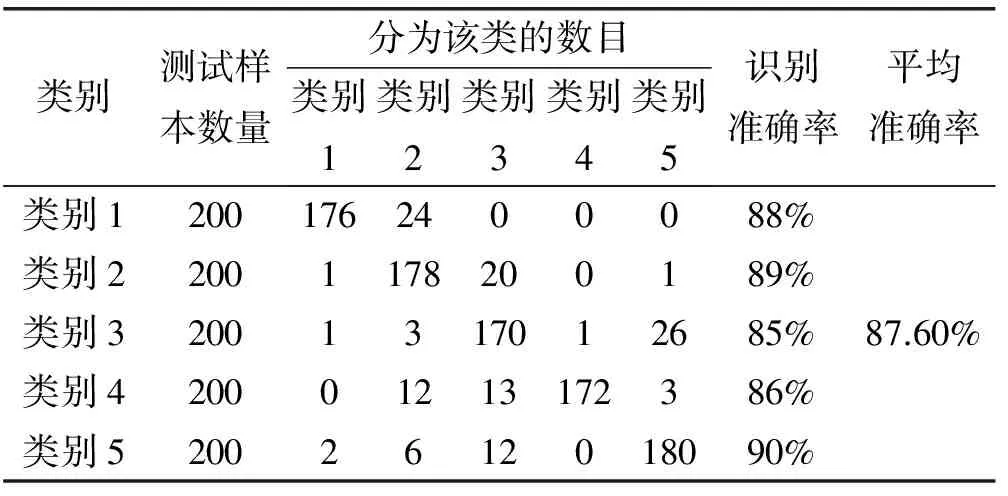
表1 基于高阶谱主曲线识别结果

在本次实验中，针对文献[9]中所提出的基于功率谱谱骨架的信号识别方法进行了对比。基于功率谱主曲线的识别结果如表2所示，发现基于高阶谱骨架的识别率相对于基于功率谱谱骨架的识别率提高了15.7%，从而也验证了高阶谱比起功率谱含有更多能够表征辐射源的信息。

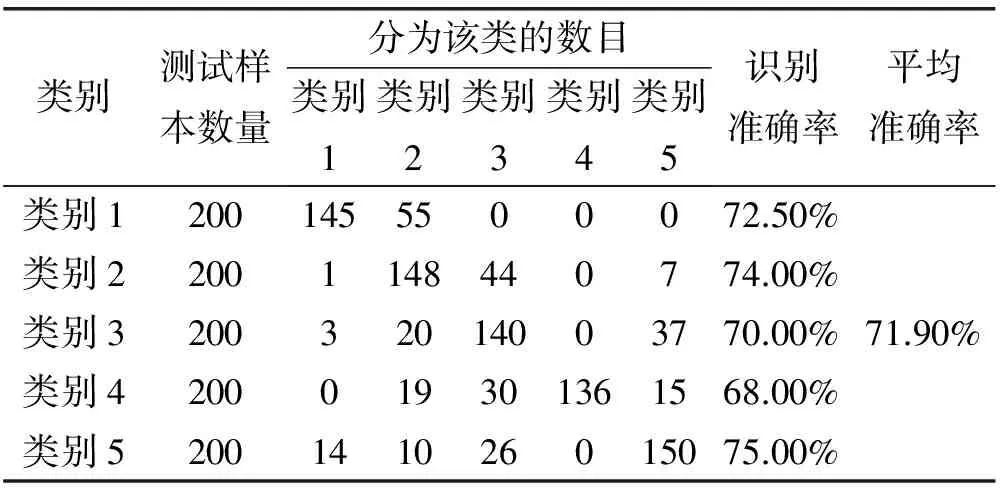
表2 基于功率谱主曲线识别结果

为了验证所提特征“高阶谱谱骨架的描述”对识别率的影响，从上面所提取的多维特征向量中剔除掉所有高阶谱谱骨架特征，用剩余的十种时频域特征进行信号的分类识别，分类识别结果如表3所示。从表中看出，若所提取特征剔除掉高阶谱谱骨架特征，识别率会明显下降，在其他参数不变的情况下，其平均识别率下降到了62.7%，说明高阶谱谱骨架特征对识别率的提高贡献很大。

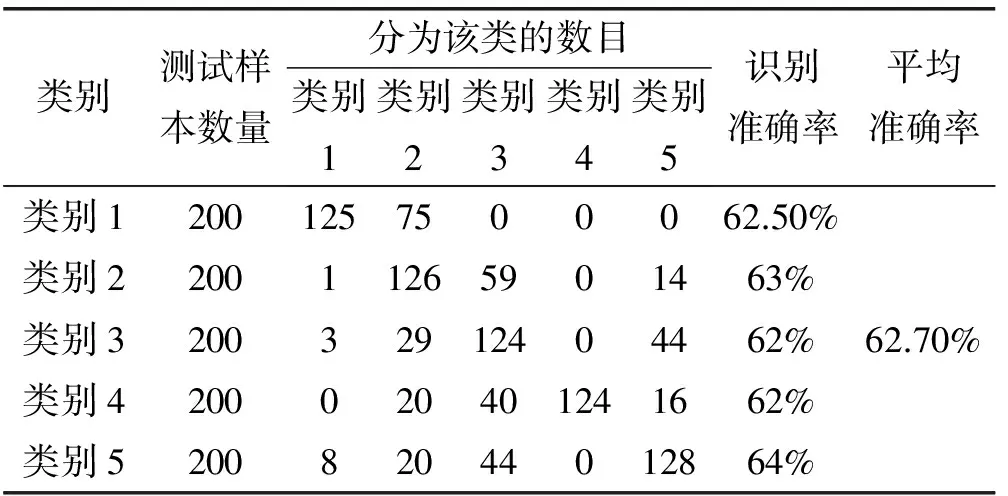
表3 剔除高阶谱谱骨架特征后的识别结果

图9更加清晰地显示出了本文方法的效果，与剔除高阶谱谱骨架特征后的识别结果对比是为了说明高阶谱谱骨架特征对识别结果的提高具有很大的贡献，与基于功率谱主曲线识别结果相对比，是为了说明高阶谱比起功率谱具有更多的特征信息，尤其是在信号处理与识别方面已成为一种有力的数学工具。

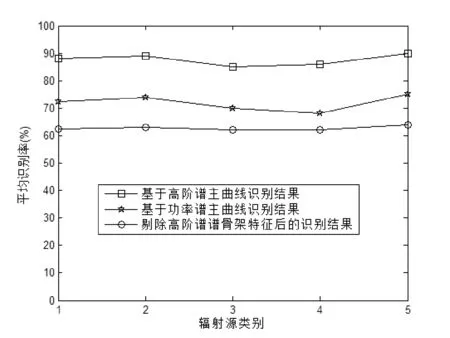
图9 识别效果对比图

6 结 语

本文在对通信信号细微特征提取与识别的研究基础上，提出并建立了一种基于信号高阶谱谱骨架的细微特征识别模型。首先求取信号的高阶谱，把高阶谱作为信号的基本特征向量，强调利用主曲线来提取信号高阶谱的谱骨架，采用分形理论对得到的高阶谱谱骨架进行比对，结合信号的时频域分析识别出个体辐射源发出的信号。不仅从理论上阐述了对比功率谱作为基本特征向量的优越之处，还通过对实际信号的大量实验，验证了本文方法的效果。

另外为了验证本文基于高阶谱谱骨架的信号细微特征提取识别模型的有效性，本文实验利用了五种不同的实际辐射源信号做个体识别实验，不仅与剔除高阶谱谱骨架特征的实验效果进行对比，也对比了基于功率谱谱骨架的识别结果。实验结果表明，本文方法得到的五种辐射源信号的特征分布具有良好的收敛性，识别结果优于现有基于功率谱谱骨架方法的识别结果，证明了本文基于信号高阶谱谱骨架的细微特征识别模型的有效性。

[1] 齐建文,陈慧娴,吴彦华,等.通信辐射源信号细微特征分析与处理[M].北京:国防工业出版社,2015:1-4.

[2] 徐书华.基于信号指纹的通信辐射源个体识别技术研究[D].武汉:华中科技大学,2007.

[3] Bertoncini C,Rudd K,Nousain B,et al.Wavelet fingerprinting of radio-frequency identification (RFID) tags[J].IEEE Transactions on Industrial Electronics,2012,59(12):4843-4850.

[4] Ureten O,Serinken N.Wireless security through RF fingerprinting[J].Canadian Journal of Electrical and Computer Engineering,2007,32(1):27-33.

[5] Hall J,Barbeau M,Kranakis E.Radio frequency fingerprinting for intrusion detection in wireless networks[J].IEEE Transactions on Defendable and Secure Computing,2005:1-35.

[6] 高迎,张迎云.主曲线在复杂指纹图像特征提取中的应用[J].计算机应用与软件,2013(9):12-15,38.

[7] 马驰,于淼,苗夺谦.改进的主曲线算法在指纹骨架提取中的应用[J].计算机工程与应用,2013(3):202-206.

[8] Verbeek J J,Vlassis N,Krose B J A.A Soft k-Segments Algorithm for Principal Curves[C]//Artificial Neural Networks-ICANN 2001,International Conference Vienna,Austria,August 21-25,2001 Proceedings.DBLP,2001:450-456.

[9] 李学成,段田东,徐文艳,等.基于软K段主曲线的信号细微特征识别[J].计算机应用与软件,2015(5):197-202.

[10] Lee T C M,Wang N H.Oh a K-Segments Algorithm for Computing Principal Curves[C]//Image Analysis and Interpretation,2006 IEEE Southwest Symposium on.IEEE Xplore,2006:183-187.

[11] 曾珍.通信电台个体杂散特征提取算法研究[D].西安:西安电子科技大学,2013.

[12] 党月芳,徐启建,张杰,等.高阶累积量和分型理论在信号调制识别中的应用[J].信号处理,2013,29(6):761-765.

[13] Gillespie B W,Atlas L E.Optimizing time-frequency kernels for classficication[J].Signal Processing,IEEE Transactions on,2001,49(3):485-496.

[14] Zhang J,Wang F,Dobre O A,et al.Specific Emitter Identification via Hilbert-Huang Transform in Single-Hop and Relaying Scenarios[J].IEEE Transactions on Information Forensics and Security,2016,11(6):1192-1205.

[15] 钱祖平,徐渊,邵尉, 等.基于高阶谱和时域分析的电台稳态特征提取算法[J].电子与信息学报,2013,35(7):1659-1605.

[16] Yuan Y,Huang Z,Wu H,et al.Specific emitter identification based on Hilbert-Huang transform-based time-frequency-energy distribution features[J].Iet Communications,2014,8(13):2404-2412.

HIGHER-ORDERSPECTRUMSKELETONAPPLICATIONTOSIGNALFINECHARACTERIDENTIFICATION

Wang Huanhuan Zhang Tao
(CollegeofInformationSystemsEngineering,PLAInformationEngineeringUniversity,Zhengzhou450000,Henan,China)

Aiming at the practical signals, a high order spectrum skeleton model which based on the principal curves of K-segments algorithm is constructed to solve the problem of signal identification among transmitters with same model. We take the information dimension and box dimension of the skeleton as transient feature, which is combined with the time-frequency domain analysis. At last, the derived feature vectors are trained by SVM classifier to recognize the signals emitted from different sources. Experiment results show that this method can classify the same model transmitters. The recognition rate can still reach 85 percent or higher in the condition of low SNR.

High order spectrum Principal curve Fractal dimension Recognition rate

2016-09-28。国家部委资助项目。王欢欢，硕士生，主研领域：信号分析与识别。张涛，教授。

TP3

A

10.3969/j.issn.1000-386x.2017.08.032