基于时间序列模型商品搜索排序

章 振 增

(上海大学 上海 210000)



基于时间序列模型商品搜索排序

章 振 增

(上海大学 上海 210000)

电商商品搜索引擎目前大多都是基于用户浏览行为与购买行为来建立搜索因子，通过这些因子计算出商品分地区的排序分值进行排序。然而这些行为数据都是属于历史数据。搜索的结果都是基于历史数据的分值计算没有前瞻性。特别对于换季商品使用该方式计算出来的搜索结果不佳，转化率不高。提出一种基于时间序列的分析方法，对部分的搜索因子采用预测数据来计算分值，以满足商品搜索中某些具有周期性季节性商品的合适排序。

商品搜索排序 时间序列分析

0 引 言

电商行业网站中搜索操作代表了用户较为明确的购买意图，搜索引导带来的成交量在一个电商平台中始终具有举足轻重的地位。搜索是用户的主要商品入口，电商网站80%的流量贡献都是来源于此，因此提高搜索转化率尤其重要。搜索引擎中召回率与查准率是检索系统中性能最重要的衡量参数，而电商领域还有一个非常重要的参数，就是转化率。转化率这个评价指标的好坏对搜索而言主要是依赖于商品的排序，也就是说排序的最终目标要把用户的需要商品优先往前排。一般用户在商品搜索结果页浏览上不会超过3页，因此排序要解决的问题是把质量优秀且符合用户需求的商品尽量集中到这前3页结果页面中，让用户在第一时间就可以看到所需商品从而提高搜索的转化率和用户体验。

电商搜索引擎中由于大部分电商搜索规则都是基于历史数据直接计算商品的权值实现，如点击、购买、收藏、评论数据等用户历史行为来计算商品的综合分数。一般情况下这些分值算出来的排序都是优良有效的，但是如果在节日与季节切换时间点上，这些排序算法就会出现排序滞后问题。换季的时候往往用户搜索时还有大量过季商品排在前面。由于这些算法的排序数据是基于用户历史行为，排序结果反应的是用户的历史需求而不是用户的当前需求，排序结果不具有前瞻性。

本文将对上面所述问题提出一种基于时间序列分析[1]结合DTW动态时间规整[2]的方法对商品的分数进行预测，以实现商品的排序结果满足用户的搜索需求。

1 时间序列分析

时间序列分析是一种动态数据处理的统计方法，通过历史数据的变化的规律建立模型分析预测变量值。时间序列是按时间顺序的一组数字序列。时间序列分析就是利用这组数列，应用数理统计方法加以处理，以预测未来事物的发展。[1]时间序列预测分析的方法主要有：简单序时平均数法、加权序时平均数法、移动平均法、加权移动平均法、趋势预测法、指数平滑法、季节性趋势预测法、市场寿命周期预测法、ARMA[8]等。

由于商品数据分析中数据量庞大，采用的算法需要简单高效，因此采用一次指数平滑法可以保证高效的计算分析。一次指数平滑法是指以最后的一个第一次指数平滑。它根据前期的实测数和预测数，以加权因子为权数，进行加权平均，来预测未来时间趋势的方法，具体公式如下[4]：

Ft+1=αYt+(1-α)Ft

(1)

式中，Ft+1为t+1期的指数平滑趋势预测值；Ft为t期的指数平滑趋势预测值；Yt为t期实际观察值；α为权重系数。

可以对式(1)进行整理成如下通用公式形式：

Ft+1=αYt+(1-α)αYt-1+…+(1-α)nαYt-

α+…+(1-α)tF1

(2)

对于式(2)，由于数据项的值并不是很大，因此在第四项以后值已经很小对预测影响不大。为了使程序计算更简单更快速，本文采用前4项的值来预测，所以预测公式可以简化如下：

Ft+1=αYt+α(1-α)Yt-1+α(1-α)(1-α)Yt-

2+(1-α)(1-α)(1-α)Ft-3

(3)

对于式(3)最后一项Ft-3是属于预测值，这里使用加权移动平均来进行估值作为预测值[7]。假设第n期的点权值为n，n-1点的权值为n-1，如此类推，一直到0，预测值公式如下：

(4)

因为目前只使用前四项的数据，所以最终可以转换成如下公式：

(5)

结合式(3)和式(5)对商品因子进行Ft+1期数据预测。

上述公式中权重系数α还未确定，根据图1、图2所示，商品销量因子有明显的季节性变动趋势，对α在0.6～0.9区间取5个点，进行实算对比[4]。这里取玉米油上海地区销量数据，用实际值与预测值的方差s2来衡量。通过取较小s2的α值作为合适值。当α=0.6时，s2值39；当α=0.65时，s2值43；当α=0.7时，s2值45；当α=0.75时，s2值42；当α=0.8时，s2值49；在排序中为了照顾近期热卖品因此指数平滑中的权重系数α取值为0.65。

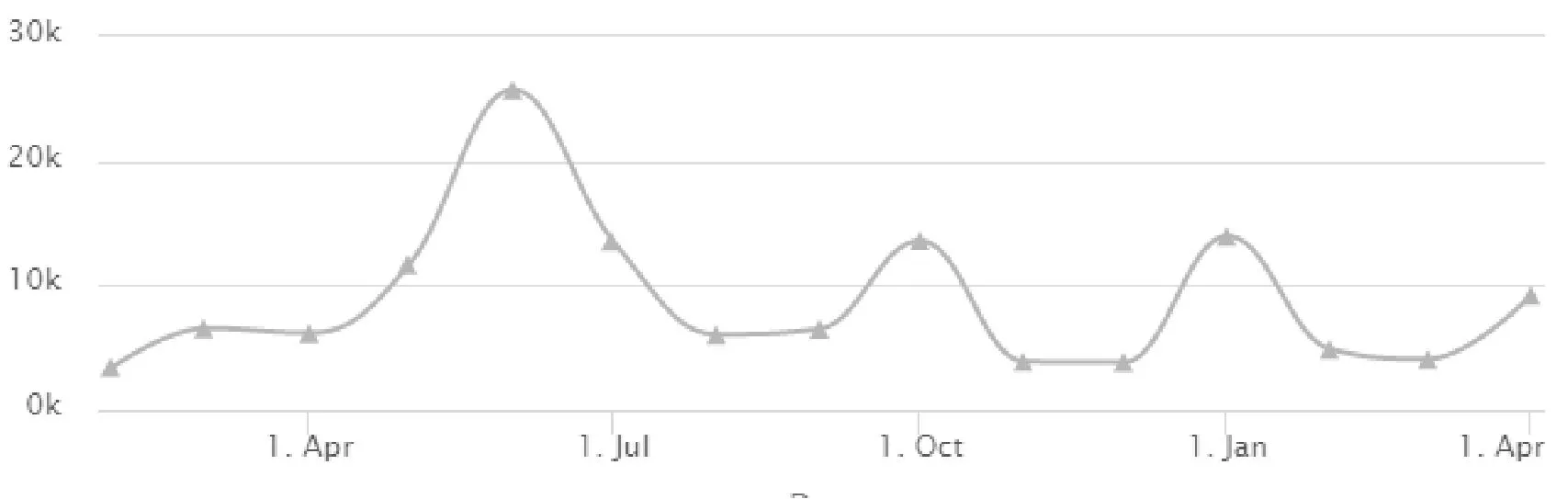
图1 食用油

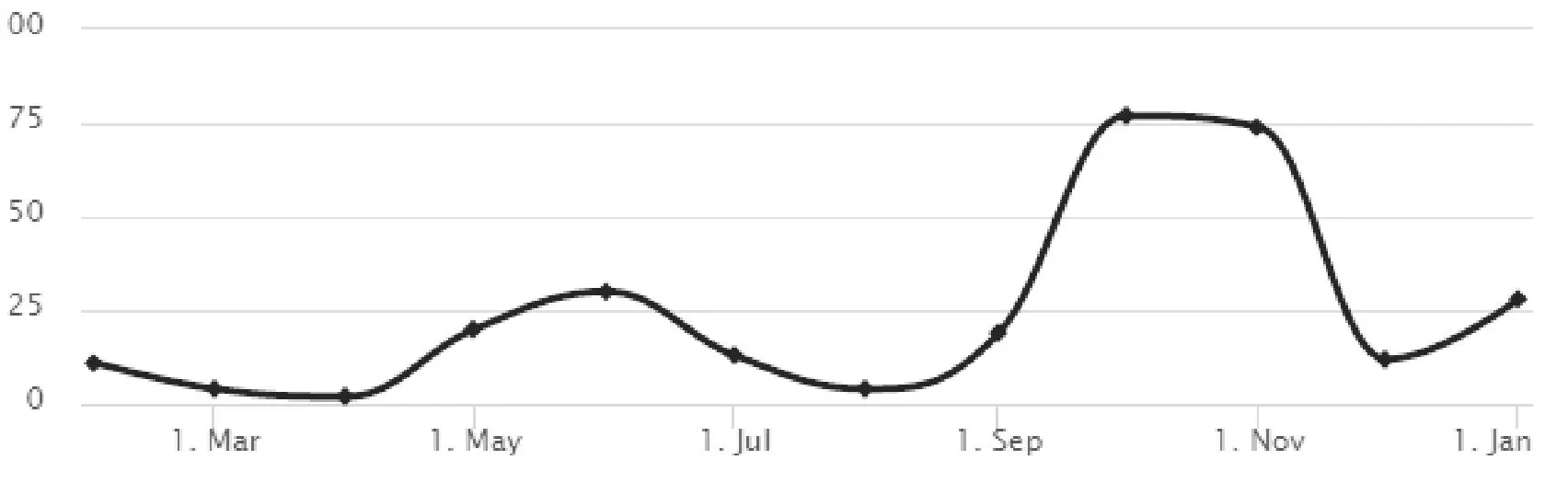
图2 春秋被

1.1 商品预测分数因子计算

商品因子数据预测如果仅仅使用当前时间的数据预测具有一定的滞后性，而且对于换季商品预测不够准确。为了提高预测准确性，在预测时间窗口上不能仅仅限于横向维度还需要增加一个预测因子使用历史每年当期该时间Ty(t+1)内的数据来进行纵向预测，最后对两个因子的计算结果加权平均。

具体算法描述如下：

1) 时间序列窗口大小设为7天，使用当前28天内的数据对未来7天Ft+1的数据进行预测，使用式(3)和式(5)可以得到Ft+1期数据。

2) 对Ft+1期数据进行归一化处理获得分数值St+1。

3) 时间序列窗口大小设为7天，使用每年同期的数据取4年的数据点，再对当前未来7天数据Fy(t+1)的数据进行预测。

4) 对Fy(t+1)数据进行归一化处理获得分数值Sy(t+1)。

5) 对不同维度预测分值加权平均作为最后的预测值S=λSt+1+(1-λ)Sy(t+1)。

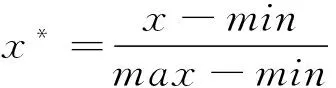
1.2 商品分数算法

如图1、图2所示，如果仅仅对单个SKU[10]来预测，由于商品上下架频繁导致数据稀疏波动较大预测效果不佳。另外对于新品上架时间过短而导致数据缺少往往无法进行有效的预测。对此，商品的最终预测分数值文中采用分类预测与商品预测两个维度分别进行预测，然后进行加权平均作为预测分数值。

具体算法描述如下：

1) 商品所处的最后一级分类进行销量等因子进行预测分数计算，得到的每个叶子节点分类值为ScoreC。

2) 对单个的SKU分别进行分值预测计算ScoreSKU。

3) 把分类预测值和SKU预测值加权平均作为该SKU的分值Ssku=λScoreC+(1-λ)ScoreSKU。

对于大部分的数据，上述预测方法可以有效地进行数据预测，但是商品预测中还有其他一些重要的影响因子，如农历节日尤其是春节、端午、中秋这些节日对特定种类商品搜索因子影响巨大。每一年的农历节日在阳历时间上都是上下浮动的，为了修正在节日点对预测数据的影响这里引进DTW算法[2]来对商品因节日效应导致预测偏差太大的问题进行处理。

2 DTW动态时间规整

DTW[2]是一种衡量两个时间序列之间的相似度的方法，主要应用在语音识别领域来识别两段语音是否表示同一个单词。DTW通过把时间序列进行延伸和缩短，来计算两个时间序列性之间的相似性。

如图3所示，上下两条实线代表两个时间序列，时间序列之间的虚线代表两个时间序列之间的相似的点。DTW使用所有这些相似点之间的距离的和，称之为归整路径距离来衡量两个时间序列之间的相似性。

图3 动态时间规整[2]

这里借鉴DTW其对时间序列匹配特性来实现对时间序列中的时间重对齐。

假设我们有两个时间序列P和C，基于每年的农历节日对应的阳历时间差不会超过30天，需要对齐的时间点为i有如下式子：

P=pi-30,pi-29,…,pi,…,pi+30C=ci-30,ci-29,…,ci

(6)

时间序列P和C，DTW实现修正在节日点预测数据不准确的算法描述如下：

1) 使用DTW算法寻找ci在序列P上的对齐点pk，Ft+1对应的时间点数据为Fp(k)。

2) 使用对齐后的数据点利用上述的时间序列预测算法进行数据预测。

DTW动态时间规整算法描述如下：

两个序列对齐点的规整路径W[9]：

W=w1,w2,…,wkmax(|P|,|C|)≤K<|P|+|C|

(7)

规整路径W的距离[9]：

(8)

Dist(W)采用欧式距离来获取，即：

Dist(W)=(pi-ci)2

(9)

最终需要的是寻找一条通过此网格中即两个序列对齐点的最短规整路径W，满足如下公式：

D(i,j)=Dist(i,j)+min[D(i-1,j),D(i,j-1),

D(i-1,j-1)]

(10)

式中，D(i,j)是所有可能路径中的最短路径。

两个时间序列之间的归整路径距离如图4所示。

图4 两个时间序列之间的归整路径距离[9]

最短路径D(i,j)寻找算法描述：

1) 构造一个61×30的矩阵网格，矩阵元素(i,j)表示pi和cj两个序列上点的距离Dist(Wij)。

2) 从一个方格((i-1,j-1)或者(i-1,j)或者(i,j-1)中到下一个方格(i,j)，横向与纵向距离为Dist(Wij)，如果是斜着对角线距离则是2Dist(Wij)，具体公式如下：

(11)

默认D(0,0)=0，D(i,j)表示2个模板都从起始分量逐次匹配，并且都是在前一次匹配的结果上加Dist(Wij)或者2Dist(Wij)，然后取最小值。

3) 起始点设为(61,30)通过回溯找到最短距离的路径,路径上的点即为最终时间序列P、C的对齐点，这样就可以找到时间序列ci对齐的点。

通过DTW算法可以找到当期与往年农历节日的同期效应点，但是由于它需要计算到每一个点，因此它对噪声比较敏感。而且该算法要求对齐的数据在节日点的数据波形有明显特征变化才可以有效的对齐。因此该算法只是对时间序列上特殊点和特殊类目的纵向预测上的必要修正，并不是在时间序列预测的任何时间点的任何数据上都是需要的。

3 实验分析

3.1 季节预测数据对比分析

这里对9月份上海地区羽绒服与T恤分类的销量数据因子进行对比实验如表1所示。

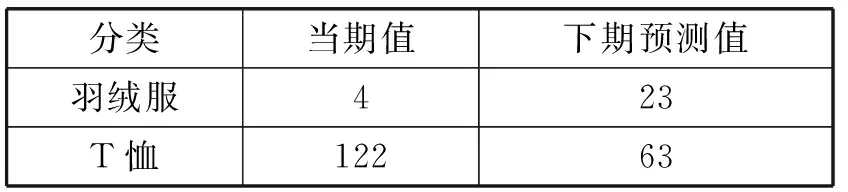
表1 季节预测实验结果对比

从表1可以看出，使用时间序列后的预测值数据对未来的趋势变化能进行有效的评估。这样使用下期预测值作为搜索排序的因子数据进行计算就可以对商品在季节交替中按趋势对商品排序权重调整，实现商品搜索显示位置的按季节趋势调整变化。

3.2 节日对齐实验分析

农历节日点引起的销量等数据波峰变化一般都不是在节日当天，因此这里Pi取值点为2015年6月8日，Ci取值点为2016年6月8日，然后对月饼分类数据进行节日对齐实验结果如表2所示。

表2 节日对齐实验结果对比

从表2可以看出，使用了DTW对齐后在节日点的预测结果上更为可靠有效。

3.3 搜索结果对比分析

对于搜索结果的优劣常见的评价方法有召回率和准确率，召回率不是本文的研究内容，准确率会影响实验结果但是也无法准确地衡量排序算法的优劣。因此这里我们对搜索结果分析采用转化率，转化率评价指标的意义表示用户需要通过几次搜索才能找到需要的商品，搜索次数越少表示该排序越有效，因而这是电商领域比较关注的一项指标。

具体公式如下：

(12)

(13)

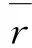
通过式(12)和式(13)可以得到搜索转化率，实验对比分析结果如表3所示。

表3 搜索结果对比

从表3中可以看出，使用了预测算法后搜索转化率效果明显增加有0.7%的增长率，说明该算法是有效符合用户搜索需求的。

4 结 语

本文主要针对电商搜索中因季节切换中排序滞后的问题以及搜索排序中转化率低下问题进行研究分析。提出了基于时间序列预测分析结合DTW进行时间重对齐修正的方法，对排序因子进行预测计算分值，以实现对商品的排序是基于未来的预测排序。实验证明该方法是有效的，可以一定程度提高搜索的转化率。当然商品排序是个复杂的系统，这些只是商品排序的众多考虑因子中的一个重要分数影响因子。最终的排序结果还需要根据Zipf 分布[5]，商品搜索结果在靠近每页搜索结果页底部的位置的奇异点点击规律[6]，以及一些实际的特殊需求如打散等需要还需对搜索结果进行最后综合的ReRank排序操作。

本文提出的算法虽然一定程度提升了转化率，但是从表3中可以看出转化率还是非常低的。转化率低下虽然不只是单一受排序影响还有其他众多因素，但是目前来看搜索排序对于转化率的提升仍然存在着很大的优化空间，未来还需要对排序做进一步研究。

[1] 百度百科.时间序列分析[EB/OL].[2016-07-10].http://baike.baidu.com/view/479624.htm.

[2] Wikipedia.Dynamic time warping[EB/OL].[2016-07-10].https://en.wikipedia.org/wiki/Dynamic_time_warping.

[3] 陈乾,胡谷雨.一种新的DTW最佳弯曲窗口学习方法[J].计算机科学,2012,39(8):191-195.

[4] Mbalib.一次指数平滑法[EB/OL].[2016-07-10].http://wiki.mbalib.com/wiki/一次指数平滑法.

[5] Wikipedia.Autoregressive-moving-average model[EB/OL].[2016-07-15].https://en.wikipedia.org/wiki/Autoregressive%E2%80%93moving-average_model.

[6] 王祥志.商品搜索中的点击分析与预测[D].上海交通大学,2007.

[7] Wikipedia.移动平均[EB/OL].[2016-07-10].https://zh.wikipedia.org/wiki/移动平均.

[8] Wikipedia.Autoregressive-moving-average model[EB/OL].[2016-07-26].https://en.wikipedia.org/wiki/Autoregressive%E2%80%93moving-average_model.

[9] Salvador S,Chan P.Toward accurate dynamic time warping in linear time and space[J].Intelligent Data Analysis,2007,11(5):561-580.

[10] 百度百科.SKU[EB/OL].[2016-07-10].http://baike.baidu.com/view/276922.htm.

SORTING OF COMMODITY SEARCH BASED ON TIME SERIES MODEL

Zhang Zhenzeng

(ShanghaiUniversity,Shanghai210000,China)

Commercial search engine which establishes search factors are mostly based on the current user browsing behavior and buying behavior, and through these factors to calculate the goods sorted by region sorting scores. However, these behavioral data belong to historical data. The search results based on the historical data of the score calculation is not forward-looking. Especially for the seasonal goods, the method of calculation of the search results are poor, the conversion rate is not high. In this paper, a method based on analysis of time series is proposed to calculate the scores of partial search factors by using prediction data, which can satisfy with the proper ordering of some periodic seasonal goods in the commodity search.

Commodity search ranking Time series analysis

2016-08-18。章振增，硕士，主研领域：人工智能。

TP391

A

10.3969/j.issn.1000-386x.2017.07.052