利用Excel Vba求解运输问题的计算机辅助算法

曾 强 邓敬源 袁明明

(河南理工大学能源科学与工程学院 河南 焦作 454000)



利用Excel Vba求解运输问题的计算机辅助算法

曾 强 邓敬源 袁明明

(河南理工大学能源科学与工程学院 河南 焦作 454000)

针对运输问题求解过程的复杂性，基于表上作业原理，提出一种利用Excel Vba求解运输问题的计算机辅助算法。首先，介绍了辅助算法原理及计算流程；其次，详细描述了辅助算法的三个关键技术，即用最小元素法获取初始基可行解的技术、用位势法求取非基变量检验数的技术及用程序进行闭合回路自动调整的技术；最后，通过案例分析验证了该辅助算法的有效性。

运输问题 计算机辅助算法 表上作业法 Excel Vba

0 引 言

运输问题是组织运营中常遇到的重要问题，运输优化能为组织带来经济或社会效益。然而，运输问题最优解的求解过程却是一项复杂而繁琐的工作，正是这种高度复杂性限制了运输问题在组织运营中的推广应用。基于此，自从20世纪40年代运输问题提出之日起[1]，学者对运输问题的求解方法进行了大量的研究，取得了较丰富的成果。

概括而言，运输问题的主要求解方法有线性规划法、动态规划法、表上作业法、图上作业法、网络解法和计算机算法[1]。运输问题是线性规划问题的特例，故可考虑将运输问题视为线性规划问题，利用线性规划方法求解。但由于运输问题决策变量多，约束条件多[2]，利用线性规划方法求解运输问题需进行大量重复计算，计算很不经济。动态规划法[3]将运输问题转化为动态规划问题，采用动态规划方法求解。但动态规划法本身比较抽象，不同的动态规划问题需建立相应的状态转移方程，难以被现场人员掌握。表上作业法首先利用最小元素法或其他方法获得初始基可行解，再利用闭回路法或位势法求取非基变量的检验数，并利用闭回路调整法进行解的调整直到所有非基变量的检验数非负[1-2]。表上作业法的计算量大，手工计算易出错、效率低。图上作业法需在图上构造边、权、边线，然后在图上求解，当产地数和销地数较多时，边、权、边线太多，易混淆，不利于实际操作[1]。网络解法将运输问题视作一个网络，采用图与网络技术进行求解。它可以更直观、快速、形象地得到初始解，但当产销地数量较多时，绘制网络图较麻烦[1]。计算机算法是将以上几种方法用计算机来加以实现，它可提高计算效率和准确性，从而提高运输问题在组织运营中推广应用的可能性。目前，在运输问题的计算机算法方面已有一些研究成果：文献[4-5]利用EXCEL的规划求解功能求解运输问题，在一定程度上提高了计算效率，但由于约束条件随着产地数m和销地数n的不同而不同，需手工设置公式及约束条件，操作繁琐、易出错，且难以获得多个最优解。文献[6-8]利用Matlab的线性规划工具求解运输问题，但因运输问题的变量多(m×n个决策变量)、约束条件多(m+n-1个独立约束方程)，其系数矩阵的结构松散而庞大[2]，导致设置工作繁杂，不利于现场人员掌握。文献[9]提出一种神经网络解法求解运输问题，虽有一定创新性，但却问题复杂化，不利于现场人员掌握。文献[10]提出一种计算机算法求解运输问题，但仅给出了总体思路，未给出详细求解步骤。运输问题的计算机算法还有遗传算法[11]、蚁群算法[12]等，但这些算法主要用于求解复杂而特殊的运输问题，不具有普适性。在现实中以传统运输问题居多，研究传统运输问题的计算机算法更具意义。

文献[1]指出表上作业法的计算量大，但因其原理相对简单、计算过程相对形象直观，因此在现实中应用最为广泛。本文基于表上作业原理，将人与计算机的特长相结合，利用计算机擅长重复计算和人擅长思考的特点，利用Excel Vba开发了一种传统运输问题计算机辅助算法。

1 运输问题数学模型

设某种物品有m个产地Ai,i=1,2,…,m，其产量为ai,i=1,2,…,m，有n个销地Bj,j=1,2,…,n，其销量为bj,j=1,2,…,n。从产地Ai向销地Bj运输单位物品的运价为cij、运量为xij。

对于产销平衡的运输问题有如下数学模型：

xij≥0i=1，2，…，mj=1，2，…，n

对于产销不平衡的运输问题可通过增加虚拟产地或虚拟销地的方式将其转化为上述标准的运输问题。

2 算法原理及流程

本文提出的运输问题计算机辅助算法依据的原理是表上作业原理。基本思路如下：(1)采用最小元素法获得初始基可行解；(2)运用位势法求得非基变量的检验数；(3)采用闭回路调整法对基可行解进行调整，转(2)，直到所有非基变量的检验数非负，找到一个最优解；若对最优解不满意(考虑到实际运营中某些特定条件的限制，最优解可能并不一定适用，导致决策者对理论上的最优解并不一定满意)，利用算法可快速获得其他最优解以供决策。图1是本文算法的计算流程。

图1 算法计算流程

3 算法关键技术

3.1 最小元素法获取初始基可行解

为采用最小元素法求初始基可行解，定义了数组D和E及大正数M。其中，D=[dij]m+2,n+2，E=[eij]m+1,n+1。

令[dij]m,n中的元素dij=cij，D的第n+1列元素di,n+1=ai，代表产地i的产量，D的第n+2列元素初值di,n+2=ai，代表产地i的余量，显然有di,n+1≥di,n+2，当产地i未给任何销地运送物品时取等号。同理，D的第m+1行元素dm+1,j=bj，代表销地i的销量，D的第m+2行元素初值dm+2,j=bj，代表销地j的欠量，显然有dm+1,j≥dm+2,j，当销地j未接收任何产地运送的物品时取等。

[eij]m,n中的元素eij用于记录产地i向销地j的运量，其值为空表示此运量为0；E的第n+1列元素ei,n+1用于记录产地i向各销地运送物品的总量；E的第m+1行元素em+1,j用于记录销地j接收各产地运送物品的总量。

在上述变量定义的基础上，按最小元素法求基可行解的步骤，设计了如图2所示的初始基可行解计算流程，其中虚线框部分解决了表上作业法的“退化问题”。输出的初始基可行解存入工作表“基可行解”中。

图2 用最小元素法求初始基可行解流程

3.2 用位势法求非基变量检验数

用位势法求非基变量的检验数分两步进行，第一步是计算位势矩阵F，第二步是根据F和成本矩阵C计算检验数矩阵G。F=[fij]m+1,n+1，G=[σij]m+1,n+1。

[fij]m,n中的元素fij=cij(对基变量)，fij=空值(对非基变量)，F的第n+1列元素fi,n+1=ui，F的第m+1行元素fm+1,j=vj，ui、vj是待求的位势值。[σij]m,n中的元素σij=cij-ui-vj(对非基变量)，σij=空值(对基变量)，Σ的第n+1列元素σi,n+1=ui,Σ的第m+1行元素σm+1,j=vj。

计算非基变量检验数的完整流程如图3所示。输出的检验数矩阵存入工作表“检验数”中，为使后续寻找闭合回路的操作更直观，采用“条件格式”将小于0的单元格置为红色。

图3 用位势法求非基变量检验数流程

3.3 闭合回路调整

图4 寻找闭合回路流程

闭合回路调整包括两个步骤，第一步是人工寻找闭合回路。在工作表“检验数”中找到最小负数检验数，以此检验数为起点，双击该单元格，然后在该单元格横向或竖向寻找一个空格。找到后双击空格，算法自动在起始单元格与空格之间画一条直线，以此类推，每碰到一个空格，可旋转90度，直到起始单元格与终点单元格相同，至此找到一个闭合回路。在工作表“检验数”中绘制闭合回路的同时，需在工作表“基可行解”中同步绘制闭合回路，并将奇数格背景置为蓝色(代表调入格)，偶数格背景置为黄色(代表调出格)。寻找闭合回路的流程如图4所示，其程序代码放在该工作表的Worksheet_BeforeDoubleClick事件中。第二步是调整运量。找出工作表“基可行解”中闭合回路中黄色单元格中最小值作为本次运量调整值，将黄色单元格的运量减去此调整值，蓝色单元格则加上此调整值，从而实现运量自动调整功能，其对应的代码放在工作表“基可行解”的“调整”按钮的Click事件中。

4 案例研究

为验证本文提出的计算机辅助算法有效性，以文献[13]中的一个案例进行了计算。

某物资供货系统有3个资源点、2个物流网点、6个需求点，各资源点的资源量、需求点的需求量、网点规模及各点间的运价分别如表1、表2所示。由于产品质量上的原因，要求A厂供给B6的资源数量不能少于700 t，不允许二次中转，求最优运输方案。

表1 各资源点数量、需求点需求量及运价

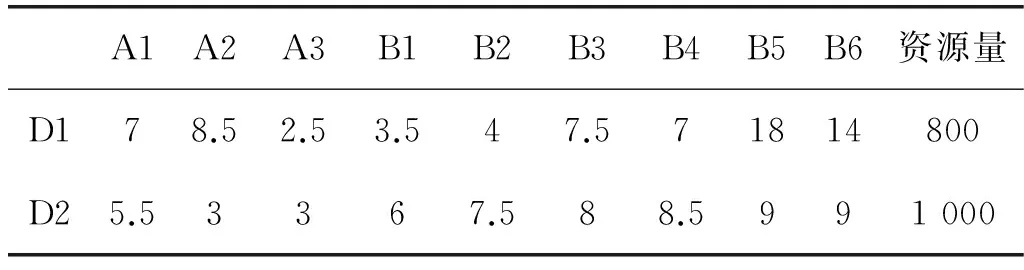
表2 网点规模及运价

由题意知A1供给B6的物资不少于700 t，可将需求点B6分成B6’和B6”两部分。其中，B6’需求量为700 t，且这700 t只能由A1供给，故可将A2、A3、D1、D2向B6运输的运价设为大数M；B6”需求量为800 t，可由A1、A2、A3、D1、D2中的任意资源点或中转点供给。综上分析，按如图5所示进行参数设置。然后利用本文提出的辅助算法求得运输问题的最优解，求解过程如图6-图15。

图5 参数设置

图6 初始基可行解

图7 非基变量对的检验数

图8 “检验数”闭合回路

图9 “基可行解”同步调整回路

图11 第一次调整后非基变量检验数

图12 一个最优解

图13 最优解对应的非基变量检验数

图14 求另一最优解的闭合回路

图15 另一最优解

比较图12和图15可见，两个最优解对应的最低成本相同，均为39 390元。整个计算过程形象直观、简便、速度快。一个10×10运输问题，其求解时间大约在2分钟之内，当然这还取决于寻找闭合回路的熟练程度。

5 结 语

运输问题是组织常面临的决策问题，在现实中具有十分重要的地位。有效降低运输问题的求解复杂度对于运输问题的推广应用具有重要研究意义。借助本文提出的计算机辅助求解算法，可帮助现场人员求解运输问题的一个或多个最优解，具有“所见即所得”的可视化效果，计算速度快，计算结果准确，并可方便地获得多个最优解供组织决策。

[1] 王有鸿, 费威. 运输问题国内外研究评述[J].商业时代, 2010(24):31-32.

[2] 甘应爱, 田丰. 运筹学(修订版)[M]. 清华大学出版社, 2005.

[3] 孙晓燕, 李自良, 彭雄凤,等. 利用动态规划法求解运输问题的最短路径[J]. 机械设计与制造, 2010(2):223-224.

[4] 陈雪菱. Excel规划求解在设施选址中的应用[J]. 工业工程, 2010,13(2):116-118.

[5] 王凤霞. Excel在物资调运问题中的应用[J]. 中国会计电算化, 2004(6):51-52.

[6] 李建祥, 唐立新, 吴会江. 钢铁工业三级供应链协调生产计划研究[J]. 计算机集成制造系统, 2005,11(3):375-380.

[7] 黄雍检. Matlab在经济管理中的应用[J]. 湖南大学学报(自然科学版), 2005,32(2):121-124.

[8] 刘希宋, 孙承华. 基于产销不平衡运输模型的燃料酒精产业布局[J]. 哈尔滨工业大学学报,2003,35(1):114-117.

[9] 程国忠. 运输问题的神经网络解法[J].计算机应用研究,2001(11):16-18.

[10] 司南, 任佳莉. 运输问题的一种计算机算法[J].计算机应用与软件,2004,21(7):120-121.

[11] 俞武扬. 多式联运运输问题的混合遗传算法[J].计算机工程与应用, 2009,45(33):10-12.

[12] 李跃光, 张远平. 一种改进的蚁群算法在垃圾运输问题中的应用[J].湖南师范大学自然科学学报,2010,33(2):18-23.

[13] 齐二石. 物流工程[M]. 机械工业出版社,2006:182-183.

COMPUTER AIDED ALGORITHM TO SOLVE TRANSPORTATION PROBLEM BY EXCEL VBA

Zeng Qiang Deng Jingyuan Yuan Mingming

(SchoolofEnergyScienceandEngineering,HenanPolytechnicUniversity,Jiaozuo454000,Henan,China)

Aiming at the complexity of solving the transportation problem, a computer-aided algorithm for solving transportation problems using Excel VBA is proposed based on table dispatching method. Firstly, the principle of auxiliary algorithm and the calculation flow are introduced. Secondly, the three key techniques of the auxiliary algorithm are described in detail, namely the technique of obtaining the initial feasible solution by the minimum element method, the technique of calculating the number of non-basic variable by the potential method and the technique of automatically adjusting the closed loop by program. Finally, the effectiveness of the auxiliary algorithm is verified by case study.

Transportation problem Computer-aided algorithm Table dispatching method Excel Vba

2016-07-04。河南省教育厅科学技术研究项目(12B120005)；河南理工大学博士基金项目(B2011-088)。曾强，副教授，主研领域：工业工程。邓敬源，硕士生。袁明明，硕士生。

TP391 C93-03

A

10.3969/j.issn.1000-386x.2017.07.008