基于CPU-GPU的B样条曲面并行刀具路径规划方法
2017-08-12黎振东俞武嘉周亚军
黎振东 俞武嘉 周亚军
(杭州电子科技大学智能控制与机器人研究所 浙江 杭州 310018)
基于CPU-GPU的B样条曲面并行刀具路径规划方法
黎振东 俞武嘉 周亚军
(杭州电子科技大学智能控制与机器人研究所 浙江 杭州 310018)
针对传统串行刀具路径规划算法效率低下和在异构硬件平台上的不兼容问题,提出一种基于CPU-GPU异构并行计算的刀具路径规划方法。方法针对双三次均匀B样条曲面,依据等参数线刀具路径规划方法的原理和OpenCL规范设计并行算法,在CPU的逻辑控制下,采用数据并行的编程模型在GPU的多个工作项上并行执行内核,将传统串行执行的等参数线法进行了并行化重构。仿真实验结果表明,该算法在CPU-GPU异构平台上生成刀具路径的时间较传统串行算法缩短1.5~11.9倍,对实现刀具路径的实时或准实时生成具有重大意义。
B样条曲面 OpenCL 并行计算 刀具路径规划
0 引 言
刀具路径是切削刀具相对于零件轮廓的运动轨迹。目前,刀具路径的生成方法趋向智能化,现有数控系统可以根据输入的数控编程数据接口国际标准STEP-NC(STEP-Compliant Data Iterface for Numeric Controls)程序得到自由曲面的几何信息,然后用等参数法生成刀具路径[1-2]。对于新一代智能数控加工系统,它要求刀具路径能够在线实时或准实时生成,但是现有的串行刀具路径生成时间较长,不能满足要求。为了满足要求,数控系统计算任务的并行化研究在国内外逐渐展开。
近年来,数控系统计算任务的并行化研究得到了快速发展,文献[3]从系统角度研究了数控系统核心任务的并行处理问题,并建立了并行处理的评价模型。文献[4]提出基于并行计算的刀具路径生成算法,实验结果证明了并行计算技术对于提升刀具路径规划算法的执行性能有相当大的作用。但是,这些并行计算都是基于操作系统多线程调度或者应用软件层面的软件级并行计算技术,真正的并行计算是硬件级多线程并行计算和异构系统的并行计算,它在数控领域中则还未见涉及[5],而在图像学、分子动力学、生物医药领域逐渐开展起来[6-7]。如今,随着IT 行业的飞速发展,越来越多不同硬件体系架构的处理器和控制器应用到数控系统形成异构系统,但传统的数控软件的架构和计算模式无法充分发挥这些新硬件的性能,阻碍了数控加工系统的进一步发展,降低了系统的开放性与兼容性。
本文利用开放运算语言OpenCL技术,使中央处理器CPU和图形处理器GPU不同架构的处理器能协同进行计算,CPU进行逻辑控制和串行计算,GPU的多个工作项执行相同的内核程序来并行求解出B样条曲面的刀具路径,实现异构系统的并行计算。实验结果表明,该并行算法在CPU-GPU异构平台上生成刀具路径的时间较传统串行算法明显缩短,使刀具路径生成能满足准实时要求。OpenCL是一个开放的、面向异构系统的并行计算标准,能充分发挥不同新硬件的性能,使并行算法具有更好的平台开放性和兼容性。
1 基本原理
1.1 双三次B样条曲面方程
给定(m+1)×(n+1)个控制顶点dij(i=0,1,…,m;j=0,1,…,n)的阵列,构成一张控制网格,给定参数u与v的次数分别为k与l,以及两个节点矢量为:U={u0,u1,…,um+k+1},V={v0,v1,…,vn+l+1}。则定义一张k×l次张量积B样条曲面,其方程为:
uk≤u≤um+1vl≤v≤vn+1
(1)
对于双三次均匀B样条曲面取k=l=3,它是由节点矢量U和V和16个控制顶点决定的,其矩阵表达形式为:
P(u,v)=UMDMTVT
(2)

1.2 刀具路径规划方法
刀具路径规划方法归纳起来可分为三大类 : 截面法、投影法、参数线法。其中参数线法是将曲面的一个参数方向作为沿切削行的走刀方向,另一个参数方向作为沿切削行的进给方向,然后将加工表面沿着选定的方向在参数定义域内进行参数细分,形成多条参数线信息,最后按照一定的规则连接参数线节点构成了刀具路径轨迹。
对于B样条曲面,由式(2)可认为它是由一系列u值不变和v值不变的B样条曲线构成的网格曲面,因此对于B样条曲面的求解,可分解为由节点矢量的每个u值和v值对应的B样条曲线所组成的网格点的求解,与等参数线法刀具路径规划方法相吻合。因此对于双三次均匀B样条曲面刀具则可以选择沿着曲面的参数(u或者v)作为沿切削行的方向,(v或者u)方向作为沿切削行的走刀方向,利用等参数线法生成刀具路径。在对参数u、v进行细分后,可以得到一系列的等u或者等v参数线。由于每条等u参数线或者等v参数线的之间不相关,则每条等u参数线或者等v参数线上对应于v参数或者u参数细分的一系列坐标值,即参数线网格点的坐标信息可以通过并行计算得到。本文取u方向作为沿切削行的进给方向,v方向作为沿切削行的走刀方向,采用等参数线法进行刀具路径规划。
1.3 CPU-GPU异构系统
在CPU-GPU异构系统中,CPU是多指令单数据流的体系结构,数据处理基本是单流水线的,更擅长的是做逻辑控制,而GPU是典型的单指令多数据的体系结构,它擅长数据计算。异构系统的体系结构如图1所示,从图中可以看出,CPU和GPU通过外部总线互连,各自拥有独自的存储空间,分别是主存和显存。程序在CPU-GPU异构系统中的执行过程大致可以分为三步:首先,将输入数据从CPU端主存拷贝至GPU端显存;接着,调用GPU执行;最后,将计算结果从GPU 端显存拷回到CPU端主存。其中在GPU上含有大量的计算单元,并且每个计算单元可以更进一步划分为一个或者多个处理单元,而计算最终都是在处理单元中完成,因此可以将程序中计算量大且可并行化执行的部分映射到GPU的多个处理单元上并行执行实现并行计算。

图1 CPU-GPU异构体系结构示意图
2 CPU-GPU平台上并行刀具路径规划算法的设计与实现
2.1 并行刀具路径规划算法的设计
对于并行程序设计,高度抽象或者模型是它的关键,模型可分为任务并行和数据并行。其中任务并行模型,CPU可以通过划分时间片来进行多线程切换方式设计,优势较GPU大;由于计算设备是GPU,因此在程序设计时采用数据并行编程模型在GPU上执行,即同一指令对多个数据元素进行操作。
根据B样条曲面的矩阵表示形式(2),将所有的u细分值组成的行向量U合并用一个大型矩阵表示,同理所有v细分值组成的列向量VT也用一个大型矩阵表示,其中每个细分值对应于一条参数线,再者系数矩阵为M、控制顶点用矩阵D表示,因此对于B样条曲面等参数路径生成抽象为简单的矩阵相乘,因此并行程序的核心就是矩阵乘法。由于参数u与v不相关,彼此没有依懒性,则可以利用分配好的工作组和工作项,每个工作项执行相同的矩阵乘法内核函数并行地求出B样条曲面参数线网格点信息,其中工作组和工作组在硬件上对应GPU的计算单元和处理单元。
2.2 OpenCL实现并行刀具路径规划算法
OpenCL作为一种新的并行计算技术,它可以调用计算机内全部计算资源,包括CPU、GPU和其它处理器。在OpenCL的执行模型中,程序分为两部分来执行,分别是主程序和内核程序,其中主程序运行在宿主机上, 内核程序运行在OpenCL设备(计算设备)上,并且主程序管理着内核程序的运行。由于CPU擅长逻辑控制,而GPU拥有大量的计算核心和强大的线程调度机制,擅长执行并行度很高的大型应用程序,因此本文宿主机选为CPU,OpenCL设备选为GPU。但是对于并行化程度不高或计算量较小的程序,如果移植到GPU上执行,由于无法隐藏多个线程存取数据的开销,以及PCI-E总线的数据传输延迟,反而会带来额外通信开销致使程序性能下降,因此对于式(2)中,系数矩阵与控制顶点矩阵相乘的计算量较小,安排在CPU上执行,而与参数矩阵的乘法运算时,参数u与v之间不相关,没有依懒性,可并行进行计算,并且计算量较大,将它放在GPU上执行。
内核程序为矩阵乘法,程序将参加计算的矩阵元素按照明确的索引代数将一对索引映射到一个索引,从而可以将矩阵转化为一维数组,因此矩阵相乘进一步转化为一维数组的运算。
主程序同理将由u、v细分值构成的参数矩阵U、V中的元素,按照明确的索引关系转化为一维数组U[i]、V[i],存储在CPU端存储器中,其中参数矩阵中每个u、v的细分值对应一条参数线;然后将在CPU端存储器中的U[i]、V[i]数组拷入已开辟好空间的OpenCL内存对象缓冲区中,该缓冲区上下文相对应,并且对与上下文关联的设备(GPU)是全局可见的,同时将该缓冲区设置为可并行访问的存储体,这样可以减少不同线程之间访问冲突或阻塞,从而降低数据传输通信开销;接着从缓冲区读取数据提供给内核在GPU上执行,多个工作项并行执行相同内核后,得到的结果为所有参数线的信息,其中每个工作项计算出的结果对应矩阵中的一行元素即一条参数线的坐标信息;最后将最终计算结果同样写入全局的结果缓冲区,然后将结果缓冲区的数据通过特定函数映射到主机内存提供给其他部分程序使用。
利用OpenCL规范设计主程序和内核的步骤:
1) 按照矩阵乘法逻辑关系编写内核函数KERNEL(_kernel void Matrixmultipli ());
2) 调用clGetPlatformIDs()发现计算机系统中OpenCL平台集合;
3) 通过clCreateContextFromType()建立上下文,用于计算设备与内存对象以及命令队列之间的通信;
4) 由clCreateProgramWithSource()创建与上下文关联的程序对象,便于程序关联的设备编译内核,利用clBuildProgram()为指定的设备构建程序对象;
5) 由CreateKernel()创建在设备上并行执行的内核,内核为__kernel void Matrixmultipli ();
6) 由clCreateCommandQueue()创建命令队列,提交到命令队列中的命令完成OpenCL的具体操作,这里操作是矩阵乘法;
7) 调用clCreateBuffer()创建缓冲区,方便进行数据的读写,通过clSetKernelArg()将内核参数和缓冲区都传递到内核,为内核计算做好准备;
8) 调用clEnqueueWriteBuffer()将要参与计算的数据信息写入缓冲区,这里是u、v细分后的一维数组;
9) 由clEnqueueNDRangeKernel()函数将内核事件加入命令队列,准备在GPU上执行,该函数的参数设定工作组和工作项的大小,即设定计算单元和处理单元的大小进行并行计算;
10) 由于缓冲区的数据,宿主机不能直接使用,须调用clEnqueueMapBuffer()和memcpy()函数将缓冲区的数据映射到宿主机,提供给CPU使用。
按上述步骤设计好程序并在GPU上执行完毕后,CPU得到所有参数线网格点的坐标信息,接着按规定的走刀方向和进出方向通过Matlab仿真出刀具路径。
3 仿真结果及分析
加速比是用来衡量程序并行化的性能和效果的一类标准,它通常定义为串行程序执行时间与并行程序执行时间的比值:

(3)
本文测试环境的显卡使用AMD Radeon(TM) R9 200 series GPU,显存2 048 MB,内存2 GB,CPU 使用AMD Athlon(TM)3.7 GHz。为模拟不同计算规模下的程序表现,以不同的采样密度分组对示例曲面进行加工域位置采样,即通过不同的u、v细分数,对曲面刀具路径生成时间进行统计,为减小系统中其他应用程序对算法程序运行结果带来干扰,结合式(3)采取重复三次操作取算术平方值的方法作为实验取值,数值结果保留小数点后一位,实验结果如表1所示。由表1数据,将u、v细分数以1 000×1 000作为基,串行程序执行时间与并行程序执行时间对比如图2所示。

表1 不同执行方式的程序执行时间

图2 并行算法与串行算法执行时间对比结果
由实验结果可知,异构平台下并行程序的执行效率较传统串行算法明显提高。通过对加速比和执行时间对比图分析可得,当点数较少时后,加速效果不是很明显,当点数继续增大后,并行计算的优势逐渐体现。因为参数u、v值细分后,随着点数的增加,串行程序循环执行的次数增多,花费时间增加快,而并行执行调整工作项的大小,计算单元增加,执行时间增长率迟缓,加速比随之增大;再者CPU是多指令单数据流体系结构,数据处理基本是单流水线的,循环操作耗时多,而GPU是典型的单指令多数据体系结构,单个指令可同时操作多个数据,耗时较少;最后,当点数较少时,CPU与GPU计算所需的线程数差不多,但GPU线程切换开销很小,所以时间较短。随着点数继续增加,CPU每个核心支持1~2个线程,须通过时间片轮转的方式来进行多个线程的切换执行串行计算。但是线程之间切换须上百个时钟周期的时间,而GPU有成千上百个内核,可以同时多个线程同时并行计算,且线程切换开销很小,因此时间明显缩短,执行时间的增长率小,加速效果明显上升。说明CPU-GPU异构并行程序的执行效率明显提高,可以缩短刀具路径的生成时间。
利用Matlab绘制出双三次均匀B样条曲面实例图和通过并行计算出的参数u、v不同细分数20×20、40×40、100×100均匀采样的刀具路径仿真如图3-图5所示。

图3 B样条实例曲面图
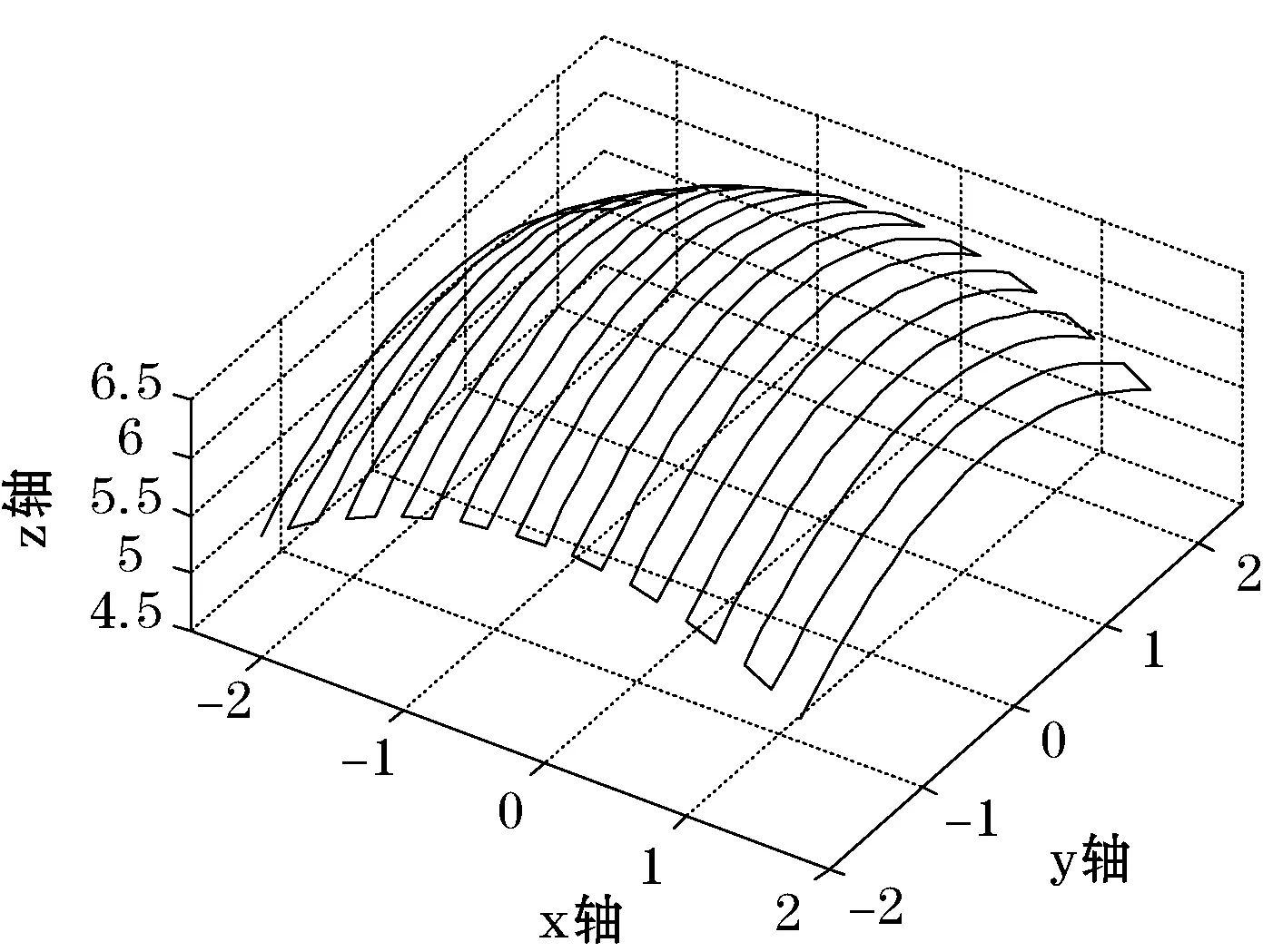
图4 20×20均匀采样

图5 40×40均匀采样
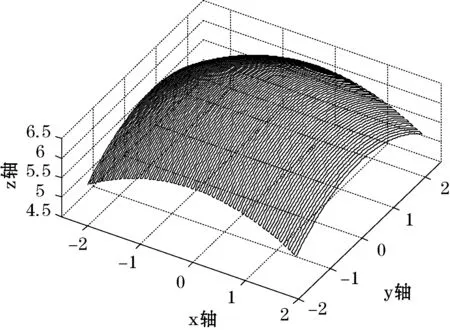
图6 100×100均匀采样
4 结 语
本文根据B样条曲面特性,利用OpenCL技术建立一种基于CPU-GPU的异构并行计算的刀具路径规划方法。通过实验结果分析,本文并行等参数线规划方法较传统串行等参数线规划方法具有更高的效率,并且实现了不同架构处理器的协同并行计算。后续可以根据OpenCL规范对算法进一步优化,进一步提高程序并行度,充分发挥GPU的强大并行计算能力和OpenCL在数控领域的应用优势,为不同硬件平台的数控系统提供一致的并行计算模式,促进新一代数控系统标准化。
[1] 富宏亚,胡泊,韩德东.STEP-NC数控技术研究进展[J].计算机集成制造系统, 2014, 20(3): 569-577.
[2] 王海瀛.STEP-NC 程序生成器及其关键技术研究[D].哈尔滨:哈尔滨工业大学,2014:3-18.
[3] 魏胜利,戴国强. 一种开放式并行数控系统研究[J].组合机床与自动化加工技术,2013,7(1):65-67.
[4] 余湛悦, 周儒荣, 庄海军,等.一种数控加工刀轨生成的并行算法[J].机械科学与技术, 2004,23(3): 266-268.
[5] 俞武嘉.基于 STEP-NC 的五轴加工刀具路径规划方法研究[D].杭州:浙江大学, 2007:95-100.
[6] 边毅, 袁方, 郭俊霞,等.面向 CPU+GPU 异构计算的多目标测试用例优先排序[J]. 软件学报,2016,27(4): 943-953.
[7] Munshi A, Gaster B R, Mattson T G. OpenCL Programming Guide[M].New York :Pearson Education, 2011:76-89.
[8] 欧阳华兵.基于STEP-NC的铣削加工智能化工艺规划系统及其实现[J].机床与液压, 2015,43(16): 22-34.
[9] 范兴山.基于异构计算的矩阵广义逆算法研究及实现[D].成都:电子科技大学,2014.
[10] 刘文志,陈轶,吴长江.OpenCL异构并行计算:原理、机制与优化实践[M].北京:机械工业出版社,2016.
B-SPLINE SURFACES’ PARALLEL TOOL PATH PLANNING METHOD BASED ON CPU-GPU
Li Zhendong Yu Wujia Zhou Yajun
(InstituteofIntelligentControlandRobotics,HangzhouDianziUniversity,Hangzhou310018,Zhejiang,China)
Aiming at the inefficiency of legacy serial tool path algorithms and incompatibility issues on heterogeneous hardware platforms, a tool path planning method based on CPU-GPU heterogeneous parallel computing is proposed. The method contraposes bi-cubic B-spline surface which is abstracted as a matrix multiplication on the principle of isoparametric line tool path planning method, and then designs parallel algorithm in accordance with OpenCL specification. Adopting data parallel programming model, it executes multiple work- items of the GPU on the core under control of the CPU logic, and reconstructs the isoparametric method as parallel execution instead of traditional serial execution. Obviously, simulation results show that this algorithm takes less time to generate tool paths on the CPU-GPU heterogeneous platforms, reduced by 1.5 to 11.9 times compared with traditional serial algorithm and it is of great significance to the tool path planning’s real-time or near real-time generation.
B-spline surfaces OpenCL Parallel computing Tool path planning
2016-07-27。国家自然科学基金项目(51405119)。黎振东,硕士生,主研领域:并行计算,刀具轨迹规划。俞武嘉,副教授。周亚军,教授。
TP391.75
A
10.3969/j.issn.1000-386x.2017.07.005
