基于改进的萤火虫算法的PID控制器参数寻优
2017-08-12李恒郭星,2李炜,2
李 恒 郭 星,2 李 炜,2
1(安徽大学计算智能与信号处理重点实验室 安徽 合肥 230039)2(安徽大学计算机科学与技术学院 安徽 合肥 230601)
基于改进的萤火虫算法的PID控制器参数寻优
李 恒1郭 星1,2李 炜1,2
1(安徽大学计算智能与信号处理重点实验室 安徽 合肥 230039)2(安徽大学计算机科学与技术学院 安徽 合肥 230601)
PID控制器的参数寻优是当代反馈控制系统设计的核心内容。PID控制器参数寻优意味着在三个参数空间域中寻找最优解,使得控制系统的性能达到最佳。为更好地对PID控制器的参数整定,引入自适应变步长策略的群智能萤火虫算法。利用MATLAB 进行仿真实验,与粒子群(PSO)算法和经典的Z-N参数整定方法进行比较。实验表明,所提算法精度高、原理简单,可高效整定PID控制器参数。
萤火虫算法 自适应步长 PID控制器 粒子群算法
0 引 言
在当今的工业过程控制中,PID控制器由于易实现、结构简单、可靠性高、鲁棒性能高等特点,被广泛应用,长久以来占据着市场的主导地位[1]。PID控制器性能与比例系数(P)、积分时间(I)和微分时间(D)有直接的关系,所以其P值、I值、D值决定了一个PID控制器性能的优劣。
PID控制器参数整定方法有传统的Z-N[1]动态特性法等方法,这些方法难以实现最优整定,并且过程相当繁琐,并且易产生大超调和震荡现象。近些年,又出现了粒子群优化算法PSO、遗传算法GA等整定方法,这些方法也存在不足。GA算法包含太多参数、具有太大的计算量和复杂的编码解码过程[2];标准PSO算法,其本质是利用自身信息、认知信息和社会信息来引导粒子的运动轨迹,当自身信息和认知信息占优势时,粒子群算法容易陷入局部最优[3],从而无法搜索到全局最优解 。
萤火虫GSO[4]算法是一种新型的群智能寻优算法,是通过模拟自然界中萤火虫在晚上通过散发的荧光素与同伴进行求偶或者寻觅食物等信息交流现象而提出的。该算法简单易理解、求解速度快、收敛能力强等优点,广泛应用于各种领域,如装配序列规划方法[5]优化、阻塞流水线调度问题[6]、网络入侵优化[7]等。标准萤火虫算法对于多峰值函数求解最优值时,能同时获得多个极值点,但是在算法后期会出现寻优精度不高、收敛速度慢等问题,降低了算法的效率[8]。为此,针对标准萤火虫算法的固定步长,提出了自适应变步长萤火虫算法,根据算法迭代的次数变化进行自适应改变。在仿真实验中,把改进的算法应用到PID控制器参数整定领域,与经典的PID控制整定方法(Z-N方法)和群智能优化算法(PSO方法)做实验比较,取得了较好的效果。
1 改进的萤火虫算法
1.1 基本萤火虫算法原理
人工萤火虫算法(GSO)将萤火虫个体作为目标函数解域中的一个解,萤火虫群会随机的分布在解域中。然后按照自然界萤火虫的移动方式进行不断的迭代运动,最后使得萤火虫可以聚集在较优的值周围,标准的萤火虫算法包括荧光素更新、概率更新、位置更新、决策域范围更新这四个步骤。其描述算法步骤如下[9]:
Step1 荧光素更新
每只萤火虫i在t+1次迭代时所具有的荧光素值,将目标函数值Ji(t+1)转化为荧光素值Li(t+1):
Li(t+1)=(1-ρ)Li(t)+γJi(t+1)
(1)
式中,ρ(0<ρ<1)是萤火虫的荧光素挥发因数,li(t)是算法在第t次迭代时萤火虫i的荧光素大小,γ是萤火虫的更新率参数,Ji(t+1)是算法在t+1迭代时荧光虫i的自适应值。
Step2 萤火虫概率更新
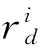
(2)
(3)
Step3 位置更新:
(4)
式中,s是每次迭代的移动步长,在标准GSO中是一个常量值,固定不变的。
Step4 决策域范围更新
萤火虫i位置更新之后,其决策域范围也会随之更新,其更新方式为:
(5)
1.2 改进的萤火虫算法
因为标准萤火虫算法的固定步长会导致算法易陷入局部最优,迭代速度慢,易产生震荡等问题。本文根据式(5)和式(6)来动态的改变算法的移动步长,提出了一种改进的变步长的人工萤火虫算法。使步长可以在算法前期保持较大值,在全局内搜索优解,防止算法过早成熟,陷入局部最优。在后期,使步长可以保持较小值,可以精确寻找最优解。
s(t)=smax(p)c
(6)
(7)
式中,t表示当前迭代次数,tmax表示最大的迭代次数。p表示一个常量,取值为0.08。
2 PID控制器参数寻优原理
2.1 参数编码
令萤火虫群的数目为N,PID控制器的三个控制参数Kp、Ki和Kd组成萤火虫寻找的问题域的维数D=3,该萤火虫群可用一个N×3的矩阵表示为:
(8)
控制系统的被控对象具有多样性,由用户根据以往的经验决定各个参数的定义域。萤火虫种群允许在定义域内随机产生。
2.2 适应度函数的选择
本文算法在不断迭代的过程中用适应度函数来判定萤火虫i所在位置的优劣,并作为以后迭代过程中的依据,使初始解移向最优解,最后聚集在最优解周围。PID参数整定有一个重要的性能指标:ITAE (The Integral of The Time Multiplied Absolute Value Of The Error),即误差绝对值时间积分[10]。该适应度函数的被控系统一般具有超调量小、平稳、快速的特点,使系统达到较好的系统性能,因此本文采用ITAE作为目标适应度函。即:
(9)
采用本文算法求最大值,因此需要处理适应度函数。在对PID控制控制器进行仿真建模时,用适应度函数的倒数值作为目标函数,即实现将目标函数的最小值转为最大值的需求。
2.3 本文算法在PID参数整定过程中的应用
三个控制参数Kp、Ki和Kd直接影响到PID控制器的性能优良,所以找到一组合适的Kp、Ki和Kd参数,对PID控制器的性能至关重要。本文算法-PID控制器的结构如图1所示。
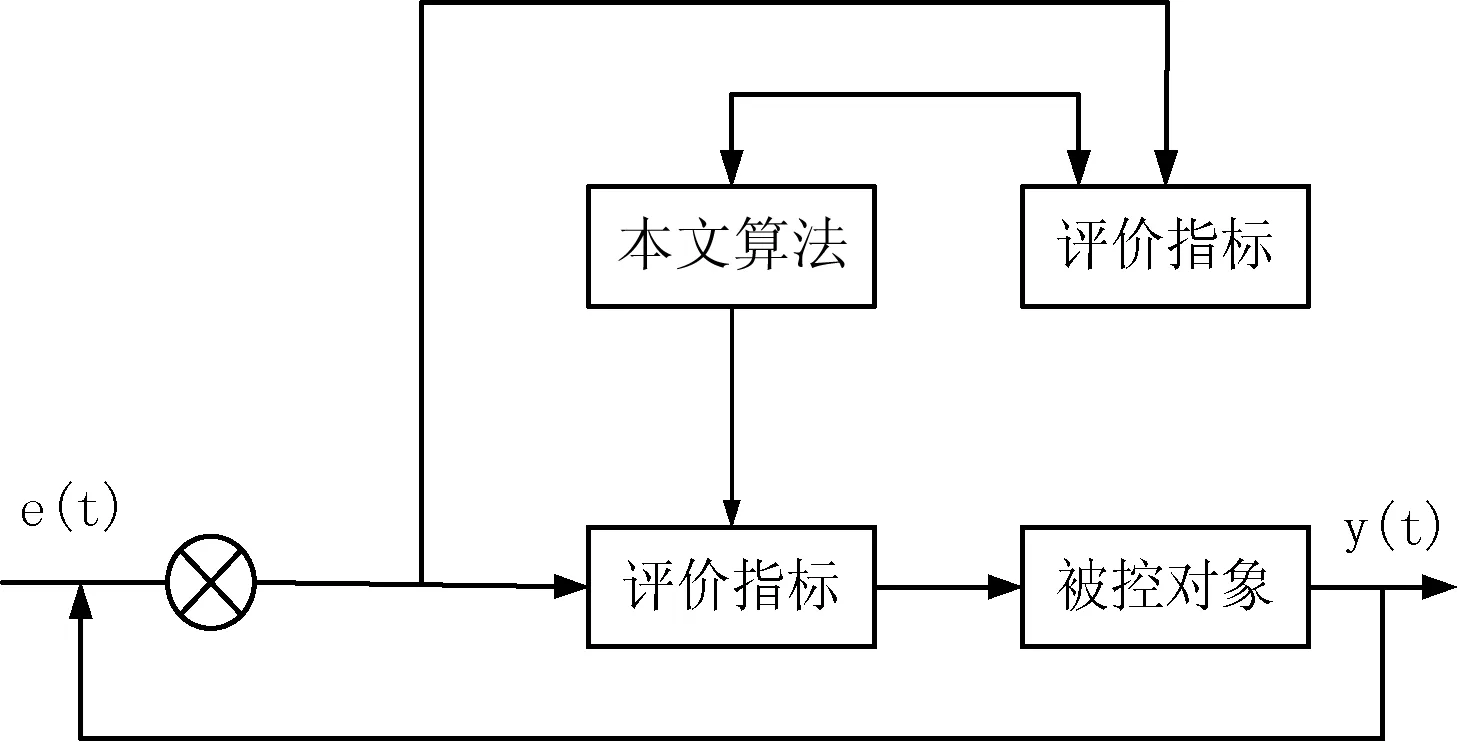
图1 本文算法-PID控制器的结构图
本文算法整定PID参数的算法伪代码描述如下:
1 初始化萤火虫种群数N=100,空间维数D=3,最大迭代次数MaxIter,荧光素挥发因子ρ=0.4,适应度提取比例为0.6,领域变化率β=0.08,感知半径为10,决策半径为10。领域值N(t)=6。
2 定义PID控制器参数Kp、Ki和Kd的位置范围。随机的在空间域中初始化萤火虫X=X1,X2,…,Xn。
3 计算适应度函数的初始值f(x)
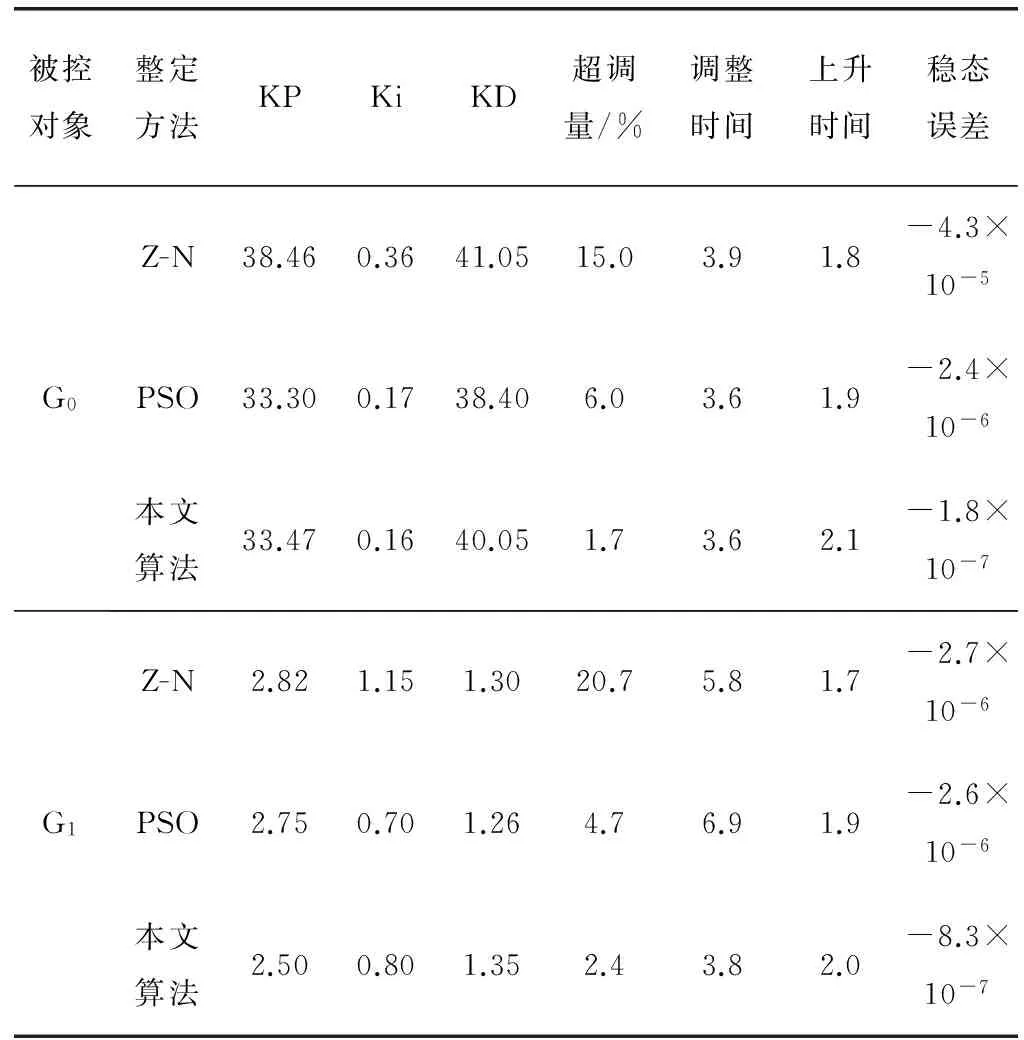
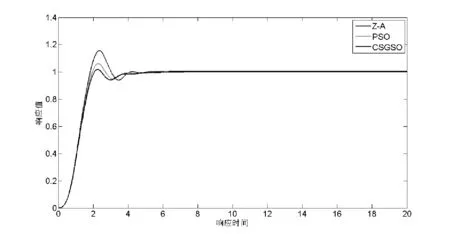
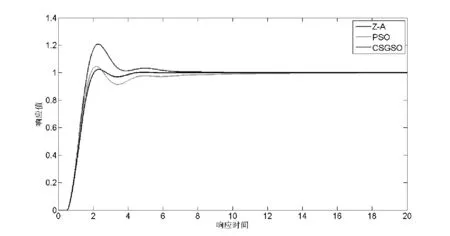
4 whilet 5 根据式(1)初始化萤火虫个体的荧光素值 6 for 每只萤火虫ido: 7 根据式(2)计算萤火虫i的动态领域集Ni(t) 8 end for 9 fori 10 iflength(Ni(t)) >0 11 for 每只萤火虫j,j∈Ni(t) do: 12 根据式(3)计算萤火虫i动态决策域内萤火虫个体j的概率 13 end for 14 按轮盘赌法选择萤火虫j 15 根据式(6)、式(7)计算算法移动的步长s(t) 16 根据式(4)更新萤火虫i的位置 17 根据式(5)更新萤火虫i的动态决策域 18 end if 19i=i+1,go to step 6 20 end for 21t=t+1,go to step 4 22 end while 23 展示结果 24 算法终止 如伪代码描述所示,本文算法整定PID控制器参数的步骤与GSO算法基本相同。不同之处是在位置更新阶段,本文算法采用的是如式(6)、式(7)所示的自适应变步长移动,而不是固定步长。 为了验证本文的设计方法,,设计了两种被控对象实例,分别是二阶滞后性仿真模型和四阶连续型模型对象,如下: (10) (11) 本文与Z-N法、粒子群算法(PSO)、进行仿真比较研究。对不同的被控对象,均采用单位阶跃信号,群规模都设置为100,最大迭代次数为Iter_Max=50。本文算法相关参数设置为荧光素挥发因子ρ=0.4,适应度提取比例为0.6,领域变化率β=0.08,感知半径为10,决策半径为10。领域值N(t)=6。本文算法采用的步长是式(6)、式(7)所示的自适应步长。 PSO算法[11]的相关参数ω=0.6,c1=c2=2。为对于式(10)表示的线性被控对象,Kp,Kd位置范围是[0,50],Ki位置范围是[0,10];对于式(11)表示的二阶惯性加滞后对象,其位置范围全部是[0,10]。 分别用Z-N、PSO、本文算法作用于PID控制器,对于不同的四阶线性对象和二阶惯性滞后对象得到的PID整定参数对比如表1所示。 表1 PID整定参数结果 分别用Z-N、PSO、本文算法作用于PID控制器,对于四阶线性被控对象得到的单位阶跃响应对比如图2所示。 图2 四阶线性被控对象单位阶跃响应图 由图2和表1可以看出,本文算法得到的阶跃响应曲线与Z-N方法相比,无论是在超调量误差、动态调整时间,还是上升时间都有较显著的优势。与PSO算法相比,控制系统的超调量优势较明显,并且在调整时间和上升时间方面也表现出一定的优势。由此可知,本文算法可以较明显提高其系统鲁棒性和抗干扰性能,以此达到良好的控制效果。 分别用Z-N、PSO、本文算法作用于PID控制器,对于二阶惯性滞后被控对象得到的单位阶跃响应对比如图3所示。 图3 二阶惯性滞后被控对象单位阶跃响应图 由图3和表1可以看出,本文算法对于惯性滞后的被控系统,表现出了较大的优势。本文算法超调量比Z-N算法、PSO算法都有明显的下降,调整时间明显变快,使系统较快达到稳态,提高系统的稳定性。所以本文算法对于工业生产过程中具有惯性滞后的被控对象具有很好的控制效果。 本文对于标准萤火虫算法存在的迭代速度较慢,易陷入局部最优等缺陷,提出了一种自适应变步长的改进的萤火虫算法,并且把本文改进的萤火虫算法应用到PID参数整定的过程中。采用MATLAB中的Simulink 环境进行仿真实验,与经典的PID参数整定Z-N方法和智能PSO优化方法进行比较。实验证明,本文算法可以较好地提高系统的动态性能,得到良好的控制效果。 [1] Ziegler J G,Nichols N B.Optimum Settings for Automatic Controllers[J].Transactions of the A.s.m.e,1942,115(2B):759-768. [2] Rao R V,Savsani V,Vakharia D P.Teaching-learning based Optimization:A Novel Method for Constrained Mechanical Design Optimization Problems[J].Computer-aided Design,2011,43(3):303-315. [3] Huang P C,Tong L I,Chang W W,et al.A two-phase algorithm for product part change utilizing AHP and PSO[J].Expert Systems with Applications,2011,38(7):8458-8465. [4] Krishnanand K N,Ghose D.Detection of multiple source locations using a glowworm metaphor with applications to collective robotics[C]//Swarm Intelligence Symposium,2005.Sis 2005.Proceedings.IEEE Xplore,2005:84-91. [5] 曾冰,李明富,张翼.基于改进萤火虫算法的装配序列规划方法[J].计算机集成制造系统,2014,49(11):799-806. [6] 郭丽萍,李向涛,谷文祥,等.改进的萤火虫算法求解阻塞流水线调度问题[J].智能系统学报,2013,8(1):34-38. [7] 周丽娟,于雪晶,魏卓.基于萤火虫群算法的网络入侵优化检测算法[J].吉林大学学报(信息科学版),2015,33(3):339-343. [8] 郁书好,杨善林,苏守宝.一种改进的变步长萤火虫优化算法[J].小型微型机计算机系统,2014,35(6):1396-1399. [9] 周永权,黄正新,刘洪霞.求解TSP问题的离散型萤火虫群优化算法[J].电子学报,2012,40(6):1164-1170. [10] Molina D,Lozano M,Herrera F.MA-SW-Chains: Memetic algorithm based on local search chains for large scale continuous global optimization[C]//Evolutionary Computation.IEEE Xplore,2010:1-8. [11] 胡伟,徐福缘.基于改进粒子群算法的PID控制器参数自整定[J].计算机应用研究,2012,29(5):1791-1794. PID CONTROLLER PARAMETER OPTIMIZATION BASED ON IMPROVED GLOWWORM SWARM OPTIMIZATION Li Heng1Guo Xing1,2Li Wei1,2 1(KeyLaboratoryofICSP,MinistryofEducation,AnhuiUniversity,Hefei230039,Anhui,China)2(SchoolofComputerScienceandTechnology,AnhuiUniversity,Hefei230601,Anhui,China) PID controller parameter optimization is the core of contemporary feedback control system design. PID controller parameter optimization means that in the three parameter space domain to find the optimal solution, making the control system performance to achieve the best. In order to optimize the parameters of PID controller, the improved GSO with adaptive step size strategy is introduced. The algorithm is simulated by MATLAB, and compared with PSO and classical Z-N parameter tuning method. Experiments show that the algorithm has high precision and simple principle, and it can efficiently set the parameters of PID controller. Glowworm swarm optimization Adaptive step size PID controller PSO 2016-06-26。国家科技支撑计划项目(2015BAK24B00)。李恒,硕士生,主研领域:智能计算与信号处理。郭星,博士。李炜,教授。 TP301.6 A 10.3969/j.issn.1000-386x.2017.07.0423 仿真实验
4 结 语
