基于多尺度角点的改进SIFT算法

成春阳 张静亚

(常熟理工学院物理与电子工程学院 江苏 常熟 215500)



基于多尺度角点的改进SIFT算法

成春阳 张静亚*

(常熟理工学院物理与电子工程学院 江苏 常熟 215500)

重点讨论一种基于角点的改进SIFT(Scale Invariant Feature Transform，即尺度不变特征变换)算法。该算法采用统一的低主曲率比值删除不稳定边缘响应点，把高斯空间中提取的角点加入到运用主曲率比值筛选后的SIFT特征点中。另外，在角点检测中，以图像区域方差来动态确定角点检测的阈值，大大提高了算法的适应性。实验证明，改进后的算法能提取更加稠密且高匹配的特征点，并且具有对主曲率比值不敏感的优点。

特征提取 SIFT算法 角点检测 改进优化

0 引 言

局部特征点的匹配是两幅图像或多幅图像之间进行局部匹配的关键技术。该技术在模式识别和计算机视觉领域，如宽基线匹配、目标识别和跟踪、图像检索和重建等领域得到广泛的应用。一般来说，局部特征点提取包括两个基本方面：特征点检测与特征点描述，而特征点的检测不仅决定了用于匹配的特征点的可靠性，而且确定了用于计算描述符的局部区域。因此特征点检测技术在特征提取中起到了极其重要的作用[1]。

SIFT算法是一种具有代表性的、性能较优的图像点特征提取算法。图像旋转、尺度缩放、亮度变化等情况不影响SIFT特征，在视角变化、仿射变换、噪声干扰的情况下也能够保持较好的稳定性。该算法被许多学者视为特征提取研究道路上的一大里程碑[2]。对这一算法的不断探索、优化甚至以此为基础开发出更进一步的算法不失为特征提取研究的一个方向。目前来说，SIFT特征提取算法在特征点检测方面还存在一定的缺陷，主要表现为：在传统算法采用的多分辨率多尺度的高斯差分空间DoG(Difference-of-Gaussian)中进行极值检测时，差分高斯算子不可避免地产生不稳定的边缘响应点，为了在初步检测出的特征点中筛除这些不稳定点，目前采用的方法是定义主曲率比值。对于图像的边缘而言，DoG响应的极值点在其切线方向上有较大的主曲率，而在其垂直方向上有较小的主曲率,所以通常将主曲率比值大于一定阈值的点看作是不稳定的边缘响应点加以剔除[3]。这种特征点筛选方法往往很难确定一个适合的阈值，不合理的阈值设置会造成特征点严重丢失或是将不稳定点带入最终的特征点集合，影响匹配效果。因为边缘点的主曲率比值较大，所以若阈值设置过大，则难以判决出全部边缘响应点；若阈值设置过小，则图像的角点和内部区域点(可以作为特征点)可能会被错误地判定为边缘点而被剔除。

为了弥补这一缺陷，研究者们也提出一些改进的措施[4-8]。例如文献[4]所采用的方案，该算法采用Canny算子检测图像的边缘信息，再比对边缘点与SIFT算法检测出的候选特征点，剔除相同点而将不同点作为最终特征点。这样的处理方式能够在一定程度上剔除掉候选特征点中的处于边缘位置的点。但是在利用Canny算子进行边缘检测时仅能针对原图像进行，因为对于高斯空间或DoG空间中的图像而言，经过多次高斯模糊后图像的边缘信息大量丢失，因此用该方法检测出的边缘特征并不具有尺度不变性。

本文提出一种新的改进算法：通过采用统一的降低主曲率比值删除不稳定边缘响应点，将SIFT特征提取与角点检测有机结合，把高斯空间中提取的角点加入到运用曲率比值筛选后的SIFT特征中。该方法一方面在一定程度上弥补误删边缘响应点，另一方面，提取出了图像角点，而角点也是需要关注的兴趣点之一。同时，该方法把阈值问题转移到角点检测中，并以图像区域方差来动态确定FAST角点检测中的阈值，从而提高了角点检测算法的适应性[9-10]。实验证明，改进后的算法能提取更加稠密且高匹配的特征点，并且具有对主曲率比值不敏感的优点。

1 SIFT特征提取算法

SIFT算法具体过程由图1所示。特征点检测部分由尺度空间极值检测和定位来完成，而特征点方向赋值和特征描述构成了特征点描述部分。

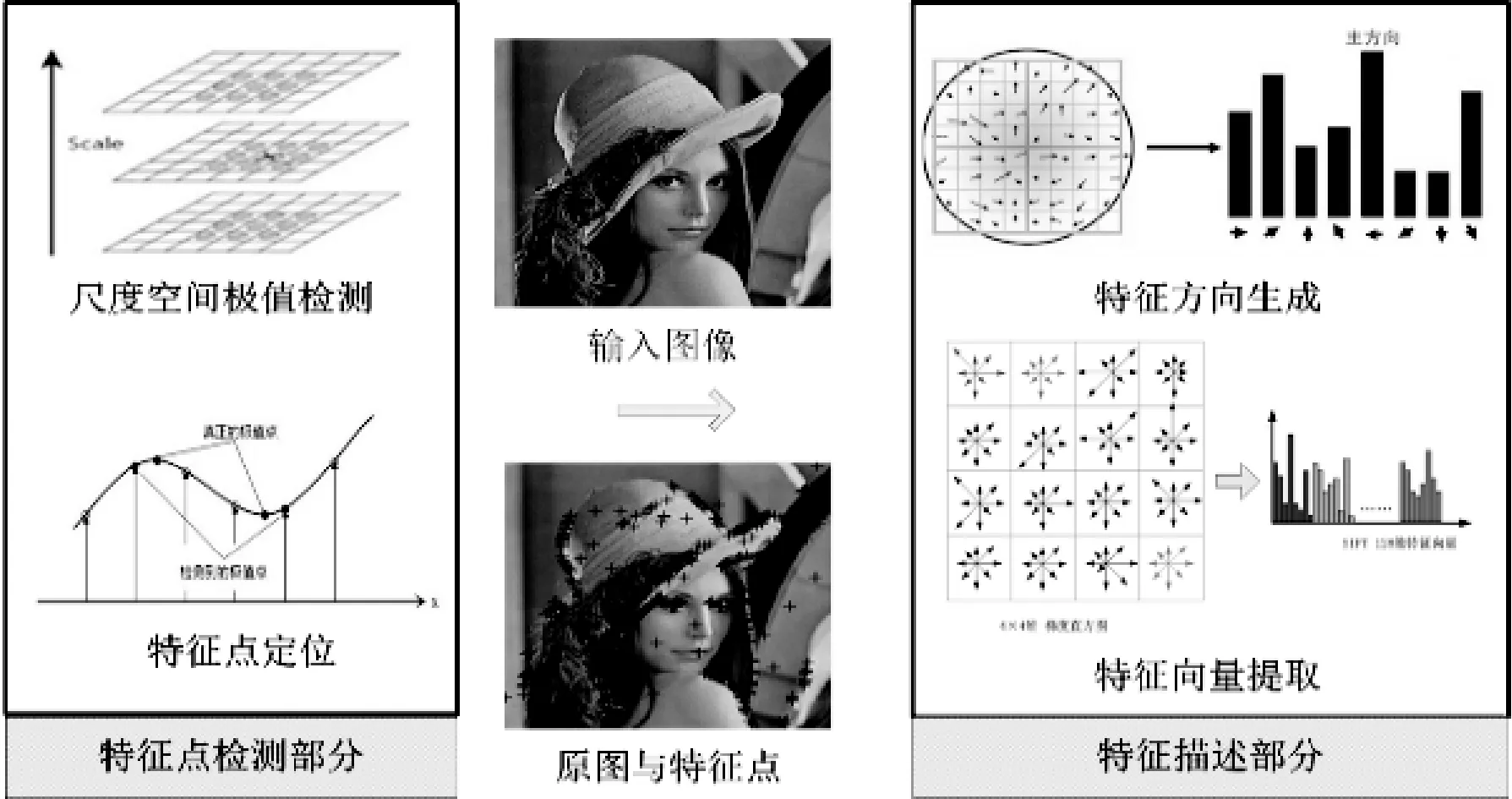
图1 SIFT算法框图

1.1 尺度空间极值检测

SIFT算法是在尺度空间内检测特征点，以此使得特征点满足尺度不变性[9]。一幅二维图像的尺度空间以及DoG算子的响应可以表示为：

L(x,y,σ)=G(x,y,σ)×I(x,y)

(1)

D(x,y,σ)=L(x,y,kσ)-L(x,y,σ)

(2)

其中,(x,y)是图像的像素坐标，G(x,y)为高斯核函数，I(x,y)为图像函数。σ即为尺度因子，反映了图像的模糊程度，其值越大表征图像被模糊程度越大。

DoG金字塔构造完成后，通过搜索DoG空间中某一层图像与相邻两层图像之间的极值点找到候选特征点，并覆盖整个尺度空间和二维图像空间。

1.2 特征点定位

当前得到的极值点是在离散的DoG空间中搜索得到的。为了获得连续空间上的坐标，利用二元泰勒展开式作为拟合函数来精确定位特征点的位置和尺度，同时剔除低对比度点和不稳定的边缘响应的特征点。

1.3 方向赋值

特征点方向由局部邻域内的梯度方向的分布直方图来确定。通常将直方图的最高峰所对应的方向赋给特征点，作为其主方向，当存在另一峰值达到最高峰的80%时，该峰值对应的方向作为特征点的辅助方向。邻域内各点梯度的幅度m(x,y)和方向θ(x,y)分别为：

m(x,y)=

(3)

(4)

1.4 特征描述

特征向量提取方法是在特征点所在尺度空间的每个区域块中统计8个方向的梯度值，并对每个梯度方向的幅度求和。若以特征点为中心取4×4个区域块，则可得到共4×4×8=128维向量来表征描述子向量。其中，梯度幅值与梯度方向利用式(3)、式(4)求得。

2 本文的改进算法

2.1 本文改进策略

本文从特征点的种类出发，将SIFT算法与典型的角点检测算法相结合，将高斯空间中提取的角点加入到运用低曲率比值筛选后的SIFT特征中，并对两者合集应用SIFT特征向量描述子。本文算法的流程如图2所示。

图2 改进策略流程图

该方法具有以下三个特点：

(1) 在DoG空间中检测出的角点仍然可能包含不稳定的边缘响应点，而在高斯空间中进行检测则规避了这一问题。

(2) 在尺度空间中进行角点检测保证了角点的尺度不变性。

(3) 将原先SIFT算法中的阈值问题转移到角点检测的阈值确定。

2.2 角点检测算法

本文的改进策略中增加了角点检测算法，这在实际应用场合会在一定程度上增加算法用时，降低了算法的实时性。为尽量避免这一缺陷，我们选用检测速度较快、实时性高的FAST(Features From Accelerated Segment Test)角点检测算法。FAST角点定义为：若某像素点的灰度值在足够大的邻域范围内最大或最小，则将该点视为角点。FAST原理如图3所示。

图3 FAST原理示意图

该算法检测角点的原理是：在一个像素点为圆心，半径为3个像素的离散化圆周上，在给定阈值t的条件下，判断在圆周上有n个连续点的灰度值是否大于I(x)+t或小于I(x)-t,即按如下公式：

(5)

其中，X为检测出的角点坐标，I(x)表示某像素点的灰度值，I(n)表示圆周上的n个点的灰度值，t为设定阈值，阈值越小检测出的角点越多。

2.3 根据区域方差确定角点检测算法阈值

区域方差是一种鲁棒的图像局部细节信息的标识方法。一般来说，方差越大，图像中的局部细节信息就越多。因此为了在不同细节类型的图像中得到相当数量的角点，本文采用区域方差来动态确定式(5)中的阈值t。经过对Corel图像库[11]进行大量的统计分析，我们发现大多数图像区域方差值V的动态范围为V∈[100,2 000]，也即Vmax=2 000，Vmin=100。同时，根据经典FAST检测算法关于阈值t的取值经验，我们将t值的动态范围设置为t∈[5,15]，即tmin=5，tmax=15。由此可确定如式(6)所示的阈值t与区域方差V之间的线性关系：

(6)

图4给出了FAST角点检测算法的实验结果，具体流程如图5所示。

图4 FSAT角点检测结果

图5 角点检测阈值确定流程图

3 实验结果与分析

SIFT特征关于旋转、尺度、亮度的不变性由经过相应变化后的图像特征与原图提取的特征之间的匹配度来体现。本文以经典的特征向量最小欧式距离作为准则，以穷尽搜索方式实施特征匹配过程。

本文选取五对细节丰富图像和五对细节简单图像组作为实验对象，分别提取特征点并匹配。实验结果如图6和图7所示，比较数据如表1、表2所示。

图6 五对细节丰富图像匹配结果对比

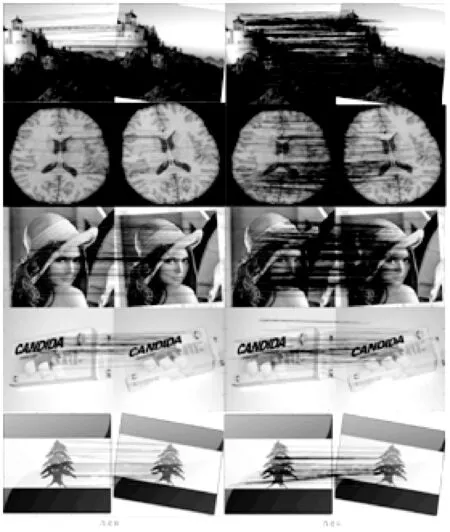
图7 五对细节简单图像匹配结果对比

图像算法阈值t特征点数匹配数/对组1SIFT/741/63051本文10.9068421117252/9355468组2SIFT/225/144142本文10.478947378486/7782708组3SIFT/744/1029335本文14.5778947410245/43161015组4SIFT/362/275105本文9.3642842116513/5966420组5SIFT/241/392111本文13.715789475099/5243412

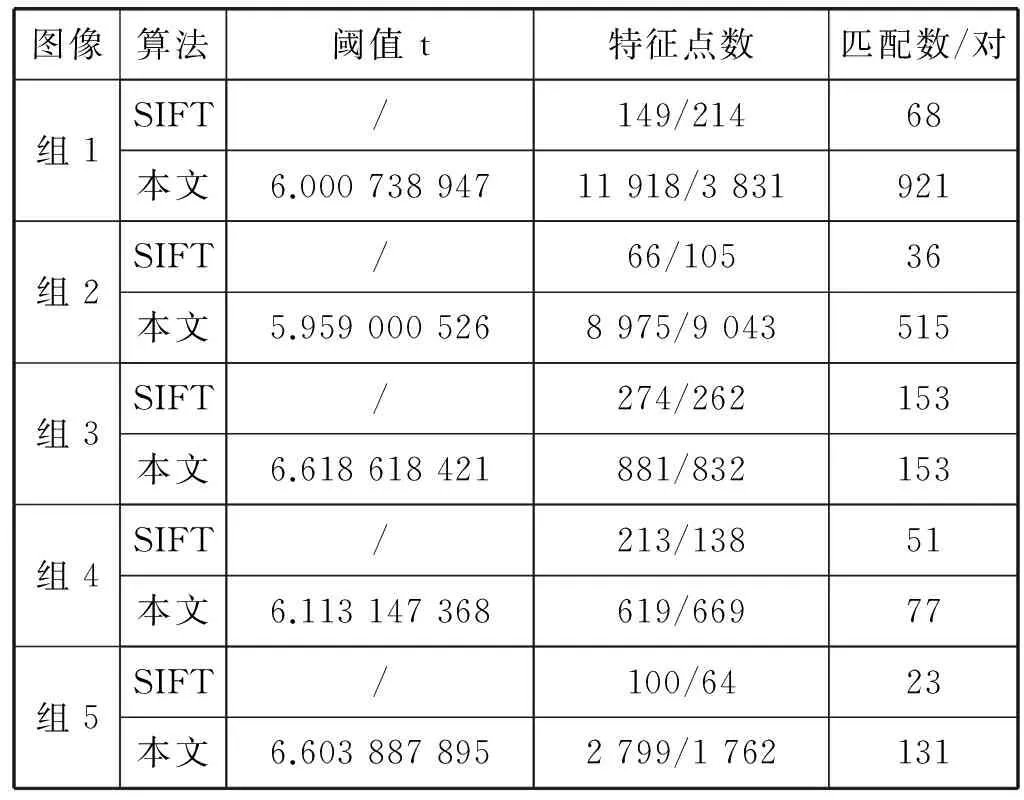
表2 细节简单图像匹配比较数据

我们针对以上图像实验结果，以匹配对数平均值为纵轴，以γ取值为横轴得到图8，用来观察主曲率阈值γ对于匹配结果的影响。可以发现：原算法可以提取出的特征点以及正确匹配点的数目较少，特别是在主曲率比值较低的情况下更少。而本文的改进算法在γ很小的情况下仍有较多的正确匹配点。因此本文算法对于γ值的变化并不敏感(实验中γ设为4)，这很好地保证了算法的适应性。

图8 γ对图像匹配的影响

从检测到的特征点的数量、正确匹配对数的角度对实验结果进行分析可以得出：

1) 本文算法提取得到的特征点数量有较大的提升，特征点的多量性得以保证与提高，特别是针对细节较为丰富的图像而言。

2) 本文算法的正确匹配对数也得到提升，因为不稳定的边缘响应点被很好地剔除，但本文所采用的匹配算法匹配率不高，提取出的特征点存在较多的冗余。

3) 由于加入FAST角点检测，本文算法的用时增加，给算法的实时性带来一定影响。

总的来讲，若是对于细节丰富的图像而言，本文算法的特征提取效果得到极大的提升，而对于细节并不丰富的图像而言，大部分实验对象的效果良好，但存在一些改进不明显的实例。因此针对细节丰富图像本文的改进策略较为适用。

4 结 语

本文探讨了数字图像的特征提取及算法，重点解析经典SIFT提取算法，同时针对其缺陷提出一种改进策略。改进算法在经典SIFT算法的基础上，利用角点检测算法在图像高斯尺度空间内求取角点，再将求得的角点与候选特征点求并集，作为最终的特征点。实验数据表明，本文所提出的算法对于细节丰富的图像应用效果突出，不仅表现在特征点数量方面，在正确匹配对数方面也有极大的提高。同时，由于有效地剔除不稳定边缘响应点，使得算法具有很好的抗干扰能力。然而，本文算法仍存在一些不足之处，由于加入角点检测使得算法的实时性降低，用时增加。此外，特征点数量以及匹配对数虽然得到质的提升，但匹配效率不高，特征点中仍然存在冗余，需要进一步完善。

[1] 杨恒,王庆. 一种新的局部不变特征检测和描述算法[J]. 计算机学报,2010,33(5):935-944.

[2] 左飞.数字图像处理：原理与实践(MATLAB版)[M].北京：电子工业出版社，2014.

[3] Lowe D G. Distinctive Image Features from Scale-Invariant Keypoints[J]. International Journal of Computer Vision, 2004, 60(2):91-110.

[4] 宋佳乾, 汪西原. 基于Canny算子和K-L变换的改进SIFT匹配算法[J]. 电视技术, 2014, 38(15):61-64.

[5] 郑永斌,黄新生,丰松江. SIFT和旋转不变LBP相结合的图像匹配算法[J]. 计算机辅助设计与图形学学报,2010,22(2):286-292.

[6] 刘佳, 傅卫平, 王雯,等. 基于改进SIFT算法的图像匹配[J]. 仪器仪表学报, 2013, 34(5):1107-1112.

[7] 张官亮, 邹焕新, 秦先祥,等. 基于改进SIFT特征和图转换匹配的图像匹配算法[J]. 计算机应用研究, 2013, 30(9):2861-2864.

[8] 汪松. 基于SIFT算法的图像匹配方法研究[D].西安电子科技大学,2013.

[9] 王蒙, 戴亚平. 基于FAST角点检测的局部鲁棒特征[J]. 北京理工大学学报, 2013, 33(10):1045-1050.

[10] 王飞宇, 邸男, 贾平. 结合尺度空间FAST角点检测器和SURF描绘器的图像特征[J]. 液晶与显示, 2014, 29(4):598-604.

[11] Chen Y X, Wang J Z. Image Categorization by Learning and Reasoning with Regions[J]. Journal of Machine Learning Research, 2004, 5(4):913-939.

AN IMPROVED SIFT ALGORITHM BASED ON MULTI-SCALE CORNER POINT

Cheng Chunyang Zhang Jingya*

(CollegeofPhysicsandElectronicEngineering,ChangshuInstituteofTechnology,Changshu215500,Jiangsu,China)

This paper focuses on a kind of improved SIFT algorithm based on the corner point. The algorithm deletes the unstable edge response points by using the unified low main curvature ratio, and combine the SIFT features points which have been screened according to main curvature ratio with the corner points of the image space of Gaussian. In addition, on the aspect of the corner detection, the variance of image region dynamically determines the threshold of the corner detection, so that greatly improving the adaptability of the algorithm. Experiments show that the improved algorithm can extract more dense and high matching feature points, and has the advantage of being insensitive to the main curvature ratio.

Feature extraction SIFT algorithm Corner detection Improvement optimization

2016-07-17。成春阳，学士，主研领域：计算机视觉及数字图像处理。张静亚，讲师。

TP391.41

A

10.3969/j.issn.1000-386x.2017.07.031