在弱标记的传感器时间序列上基于突变的事件分类
2017-08-12汪雅雯
汪雅雯 王 鹏 汪 卫
(复旦大学计算机科学技术学院 上海 200433)
在弱标记的传感器时间序列上基于突变的事件分类
汪雅雯 王 鹏 汪 卫
(复旦大学计算机科学技术学院 上海 200433)
随着传感器广泛应用于各个领域,在传感器生成的时间序列上识别事件越来越受到广泛的关注。针对震荡的传感器时间序列,提出事件分类算法BEC。对于原始长时间序列和标记时间点作为类标签,BEC主要解决了两个问题。首先是将标记时间点扩展为包含充分信息的子序列以分类,再者是提取基于突变的特征以训练分类模型。实验结果证明,无需大部分时间序列分类问题中不现实的假设和太多人力干预,BEC提取的基于突变的特征能够充分描述事件,极大保留事件中关键信息,在现实数据集上的表现优于现有的时间序列分类算法。
时间序列 分类 传感器数据 弱标记
0 引 言
传感器越来越多的应用于监测各类事件的发生,比如穿戴设备识别跑步、跳绳等运动;桥梁监测系统监测爆破、船撞等。但是,鉴于传感器数据的特征,传统的时间序列分类算法并不能适用于传感器时间序列的分类问题。
1) 对于传感器产生的时间序列,事件标签一般是原始长时间序列上的标记时间点。比如在桥梁健康监测系统中,描述爆破事件为“桥体在13:39发生爆破”,这里标签并不是事件发生的完整过程,而是事件进行中任何可能的时间点。如图1所示,图中例举了三次爆破,标记时间点在爆破事件发生时间段内的任意位置。而在传统时间序列分类问题中,长时间序列被人为切分为若干等长的片段来表示事件[1-2],这种不现实的假设也出现在时间序列领域常用的UCR数据集[3]中。在现实情况中,要么无法得到精确的事件切分,要么需要消耗大量的人力来完成。而且,不精确的分段会极大地影响分类的准确度,这种情形称为弱标记的时间序列[4]。

图1 爆破事件例举
2) 现有的特征提取算法对于传感器事件分类问题而言,无法提取包含足够信息的特征。文献[2]提出的Shapelet提取的是原始序列中最具备区分性的子序列,使用欧几里得距离来衡量相似度,但是即使传感器数据看上去很相似,直接在原始序列上比较相似距离仍然有很大的差别。如图1所示,尽管三个事件同为爆破,但由于爆破强度、爆破位置等不同,反映在时间序列上细节差异相当大。另外选取全局特征的方法,比如文献[5]中基于DWT的特征提取方法丢失了许多细节信息。文献[6]提出的SAX-VSM将时间序列转化为SAX单词,采用类似文本分类的方法训练分类模型,但是忽略了SAX单词之间的位置信息,而位置信息这一点在传感器数据中相当重要。
本文针对传感器上的时间序列分类问题的特征,提出了基于突变的分类算法BEC。首先,本文提出基于突变的特征的定义。算法并非直接从原始时间序列中提取特征,而是挖掘不同幅值的的突变并组成异常波动序列。为了能够对齐不同事件的异常,首先将异常标准化为二维数据点的序列,然后借鉴PAA[7]的思想来构造特征向量。另外,为了能够将标记时间点扩展为标记子序列,BEC算法将窗口作为参数,使用DIRECT[8]来学习得到最优窗口。实验证明BEC能够很好地应用于现实情境下的传感器数据,基于突变恰当提取事件特征,在现实数据集上的表现优于现有的时间序列分类算法。
1 问题定义
1.1 基本定义
定义1 时间序列S={s1,s2,…,s|S|}是一组有序的实值序列。
定义2 时间序列子序列S[i,j]={si,si+1,…,sj}是时间序列S的一段连续的分段。
定义3 事件E={E1,E2,…,Em}是一组现实情境中的行为,而Ei表示的是一个事件类别。
实际上,并非如同在文献[1-2]中所展示的那样,现实中的时间序列分类问题中不可能预先存在能够完全对齐的等长序列[4]。原始的标记数据一般是原始长时间序列,以及标志事件发生的标记时间点。BEC算法的输入是时间序列S和一组事件实例。
定义4 事件实例EIj={t1,t2,…,tmj}包含mj个标记时间点,对应事件类别Ej。
1.2 问题阐述
对于给定的时间序列S和一组事件实例{EI1,EI2,…,EIn},BEC通过提取特征训练模型来学习如何区分不同的事件。对给定的查询时间点tq,根据BEC训练得到的参数建立分类模型进行分类。
更直观地说,BEC解决的是在tq周围一段时间内发生了什么事件的问题。算法并不假设在原始序列上已知的理想片段,而是通过训练学习获取能够充分描述事件的模式。
2 算法概要
首先对事件作出以下合理的假设:
1) 事件的发生能够以异常波动的形式表现在传感器产生的时间序列上。如果没有事件发生,时间序列一般表现为有细微噪声的平稳状态。
2) 事件在时间序列上产生一些波动,其中具有最高峰值的波动被视为由事件直接影响产生。同时,这些波动之间的联系在事件识别中有很重要的作用。
3) 不同的事件反映在时间序列上会产生不同的异常波动,可以通过提取适当的特征来区分事件。
基于以上的假设,本文提出基于突变的事件分类算法BEC。对于给定的时间序列S和一组事件实例{EI1,EI2,…,EIn},为了避免不必要的处理整条序列,首先将每一个事件实例的时间点依次扩展为时间序列子序列。以时间点ti为中心,得到长度为L的子序列S[ti-L/2,…,ti,…,ti+L/2]。由于扩展子序列只是为了降低后续工作的工作量,所以L并不是一个非常敏感的参数,可以根据实际需求设定。后续的工作在得到的子序列上进行。
1) 在由事件实例的标记时间点得到的子序列上提取突变点,这些突变点指示可能发生的事件,是BEC算法分析的基础。
2) 将突变点划分为不相交的集合组成异常波动,它们是事件反映在时间序列上的表征。为了更好地描述异常波动,从集合中选取具有代表性的点表示异常波动。
3) 为了不仅能够准确描述事件特征,也能够对事件进行相似性度量,规整化观测窗口中的异常序列,得到特征向量。
4) 训练分类模型,学习相关的参数,对于给定的标记时间点,根据提取的特征和训练得到的分类模型自动区分不同的事件。
3 特征提取
首先在原始序列上提取突变并组成异常,然后在观测窗口中处理异常以获取特征。
3.1 从时间序列到突变
突变,指的是在平稳时间序列上罕见出现的数据点,可以指示可能发生的事件,因此概率模型通常被用于挖掘时间序列上的突变。由于仅将突变作为事件的指示而无需太过于精确,BEC没有选择复杂的时间序列模型,而是拓展了文献[9]中的方法。
大多数事件体现在时间序列上同时存在正负向的突变,如加速度数据。因此,BEC将数据按照X轴切分为正负向,并分别提取双向的突变。为了表述方便,在后文中仅按正向进行阐述。
BEC将位于指数概率模型末端的数据点视为突变点,随机变量X的指数分布累积分布函数如下:
P(X>x)=eλx
(1)

(2)
在指数分布概率模型的末端设置阈值,将超过阈值的称为突变点。注意需同时计算正负向的阈值。
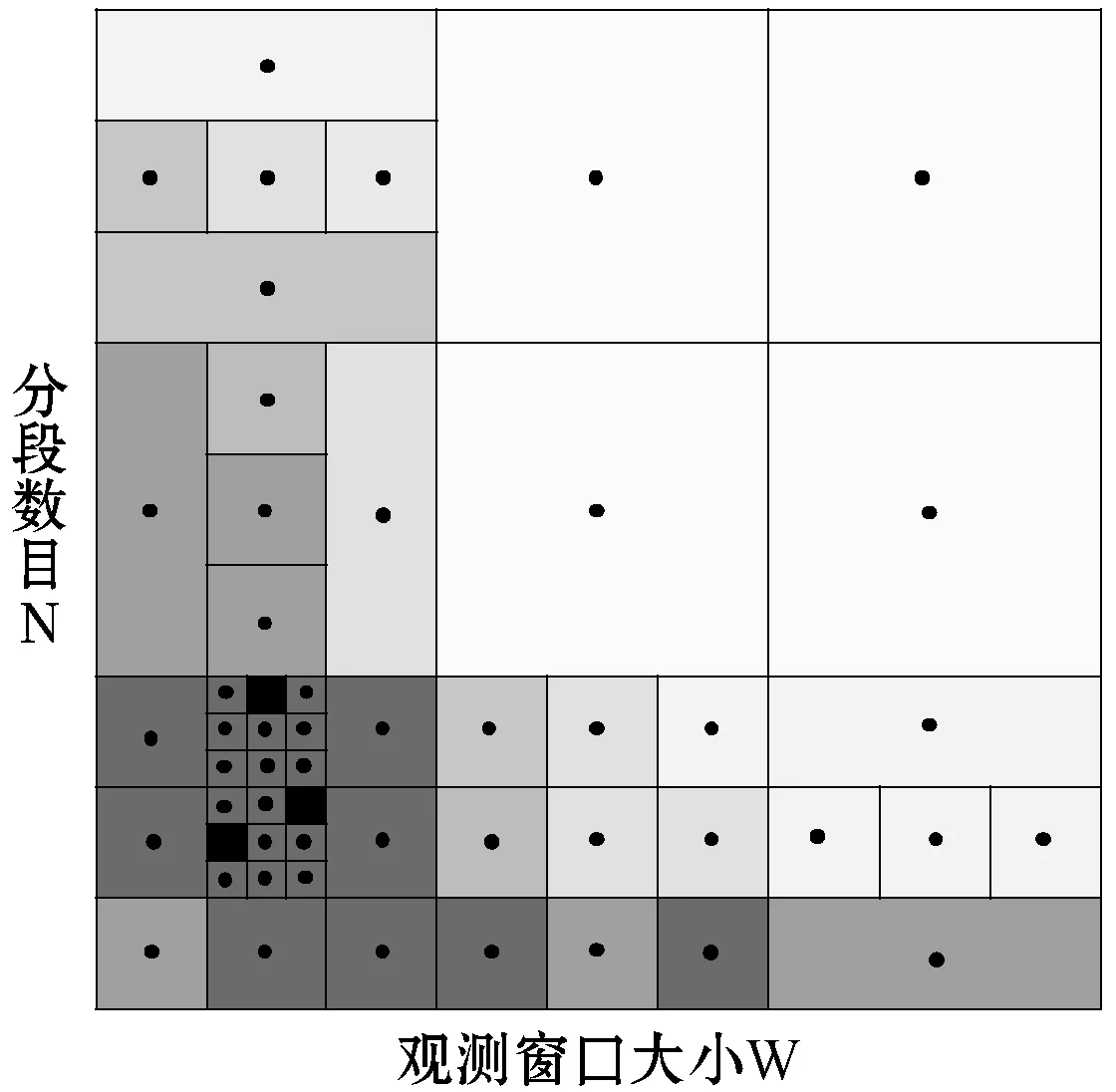
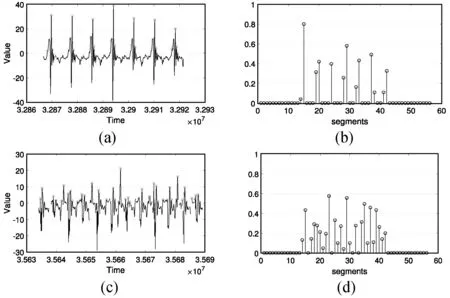
由于在整条时间序列上计算阈值具有较大的偏差,BEC在时间序列上滑动重叠窗口来计算动态阈值。首先针对每个窗口计算得到阈值,在窗口重叠的部分计算相邻窗口内对应的阈值均值。对于给定的参数l,以步长l滑动长度为2l的窗口,即{W1,W2,…,WL/l-1},其中Wi=S[(i-1)×l+1,(i+1)×l],(0 图2 突变挖掘示意图 定义5 对于事件实例的子序列,突变B的序列是一组有序的超过动态阈值的突变点{b1,b2,…,b|B|}。bj=(tj,vj)包含时间和数值两个维度。 bj={(tj,vj)|vj>δj∧tj∈Wj∧tj∈Wj+1} (3) 经过实验证明,参数P对分类结果并不敏感,而l可以根据领域知识设定,所以不需要通过训练得到。 3.2 从突变到异常 独立的突变点对于数据分析而言有些过于琐碎,因此BEC将距离足够近的突变点聚集称为异常。 距离足够近指的是在时间维度上的距离,采用简单的基于阈值的方法。如果两个相邻突变点之间的时间间隔在阈值τ以内,那么认为它们距离足够相近。而τ能够依据相邻突变点之间的时间间隔的统计值进行设置,如图3所示,相邻突变之间的时间间隔大量聚集于一个区段之内,也就是设定τ的依据。此案例中将τ设置为200。 图3 PAMAP数据集[10]中相邻突变时间间隔统计图 BEC根据阈值将突变序列{b1,b2,…,b|B|}划分为不相交的集合G={g1,g2,…,g|G|},gi表示如下: gi={bri-1+1,…,bri} (4) 其中1<… BEC重点关注异常两个方面的特性。首先是集合中具有最大峰值的突变,再者是异常的分布。从突变集合gi中选取具有最大峰值的突变点来表示它。 定义6 异常ABi是突变集合gi中最具代表性的数据点,表示为: ABi= {bri-1+k|bri-1+k∈gi∧vri-1+k= max{vri-1+1,…,vri}} (5) BEC用单个突变点表示异常,由此忽略原始数据中不重要且多种多样的细节信息,比如时间序列如何震荡达到最大峰值。 3.3 从异常到特征 BEC规整化观测窗口中的异常以提取特征。首先,阐述观测窗口的概念。 3.3.1 观测窗口 上文中将事件实例的标记时间点扩展为时间序列子序列来避免不必要的数据处理,但是子序列对于分类而言太过于模糊。因此BEC在子序列中选取更为精确的窗口来区分不同的事件。观测窗口有以下两个准则: 1) 观测窗口中一定包含表示类标签的标记时间点。 2) 如果观测窗口中包含多个异常,其中具有最大峰值的异常应当位于观测窗口的中心。因为该异常是事件反映在时间序列上最显著的表征,如此能够更精确地匹配对齐不同事件的窗口。 但是在现实情境中,不可能预知合适的观测窗口,同时已知的类标签是标记时间点。显而易见,观测窗口的大小和位置都需要通过训练得到。在下一节详细阐述基于DIRECT训练观测窗口,现在假设已知观测窗口,解释如何在给定的窗口中提取特征。 对于每一个事件实例,观测窗口Wob={AB1,AB2,…,ABω},其中ω表示观测窗口Wob中异常的个数。对不同的事件实例,其观测窗口中的异常个数是不同的。 3.3.2 异常标准化 对不同的事件实例,BEC描述的是异常的值和位置之间的关系。比如爆破事件是快速下降的剧烈震荡,而后续几乎没有其他波峰;而海浪则是包含多个相近峰值和时间间隔的波峰。但是,由于异常的数量和位置各不相同,无法直接度量异常的相似性,因此,BEC在观测窗口中基于异常构造N维特征向量,以欧几里得距离衡量异常之间的相似度。 定义7 对于事件实例的观测窗口,特征F=〈f1,f2,…,fN〉是一组N维对齐的向量。 根据异常点之间的相对位置,BEC将异常序列{AB1,AB2,…,ABω}标准化为时间及数值的二维空间[-1,1]×[0,1]上ω个数据点。令ABmax=(tmax,vmax)表示异常序列中具有最大峰值的异常,其对应数据点为(0,1)。对异常点ABi,通过如下公式计算得到对应的被映射点(0≤i≤ω): (6) 例如,{(3,1),(4,5),(6,1)}映射为{(-0.5,0.2),(0,1),(1,0.2)}。 尽管将不同事件实例的异常映射到相同空间,但是由于异常是离散且分布不规律的,仍然无法直接进行相似性度量。BEC将时间维度划分为N段,即{seg1,seg2,…,segN},用实值表示每个分段segi。这里N是分段个数,表示对异常位置偏移的容忍度,将在下一节详细阐述如何训练得到N。需要强调的是,不同的事件实例分段N值是相同的。 (7) 接下来,BEC使用欧几里得距离度量特征F和F′之间的相似度。 最近邻分类算法在时间序列分类领域被证明是极其有效准确的分类模型,BEC采用K-NN(K最近邻)作为分类模型。在训练模型的阶段,学习得到观测窗口参数以及分段数目N。对于每种事件实例,BEC创建二类分类器,将该事件实例作为正类,余下的作为负类。 4.1 模型训练 BEC使用基于DIRECT[8]和交叉验证的方法训练观测窗口大小W和分段数目N。 DIRECT是一种采样策略算法。对于在搜索空间上的函数,DIRECT极其有效的迭代寻找全局最优点。在BEC算法中,搜索空间是一个二维空间,表示为R(一个维度是观测窗口大小W,另一个是分段数目N)。首先,DIRECT在R的中心点(w0,n0)计算误差函数,然后DIRECT依据中心点和误差函数将搜索空间切分为更小的子空间,这个过程是迭代进行的,直到误差函数收敛。通过有效的采样策略,DIRECT能够智能定位子空间并快速收敛到全局最优值。DIRECT和交叉验证的示意图如图4所示,黑色正方形的中心点表示低误差率,而灰色正方形的中心点表示高误差率。 图4 DIRECT和交叉验证示意图 BEC对给定参数(w,n)进行如下三个步骤:首先根据事件实例定位大小为w的观测窗口,然后在观测窗口中获取异常的特征,最后使用交叉验证来计算(w,n)的误差函数。 用如下的方法来定位观测窗口。对于给定的标记时间点t和观测窗口大小w,要获得观测窗口Wob=[r,r+w-1]。Wob被初始化为[t-w/2,t+w/2],在窗口中找到具有最大峰值的异常,并将其置为新的中心。根据该中心创建一个新窗口,在窗口中寻找下一个具有最大峰值的异常。这个过程直到窗口不再发生变化或者标记时间点不再位于窗口中而终止。 根据观测窗口和分段数目,BEC针对每个标记时间点提取特征,并使用留一交叉验证法来计算参数对的误差函数。 4.2 分 类 给定查询时间点tq,BEC在训练得到的观测窗口W中依据分段数目N提取特征Ftq。使用欧几里德距离的K-NN分类器对Ftq进行分类,BEC通过K最近邻决定时间点tq的类标签。 本节实验证明BEC在现实问题中具有非常好的应用,在PAMAP数据集[10]和桥梁健康监测数据集上与现有的时间序列分类算法比较。 BEC算法的输入是标记时间点作为类标签的原始时间序列,而不是一组经过预处理的时间序列子序列。首先将类标签随机分为训练集和测试集。对于其他作为对比的方法,根据训练得到的观测窗口从原始时间序列中提取子序列并组成训练集和测试集。 为了避免将对比实验结果归因于本文子序列提取方法的质疑,在不同的观测窗口参数上进行实验比较。同时公平起见,在不同的数据集上均训练各个算法以得到最优的分类结果。 实验在Intel Core i5-4690 3.50 GHz CPU以及16 GB内存的机器上进行。BEC用Java实现,SAX-VSM和RPM的源代码由原作者提供。 5.1 在PAMAP数据集上的应用 PAMAP数据集记录在身上不同部位佩戴传感器的实验对象进行各种活动的数据,在实验中使用的是PAMAP2数据集中位于脚踝部位的Z轴加速度数据。数据集的原始数据是一条长时间序列,以及标记为多个时间区段的不同活动标签。在不同事件对应的时间区段内随机选取一些时间点作为类标签。 文献[11]中比对欧几里德距离的最近邻、DTW距离的最近邻、Fast Shapelets以及数据集原作者提出的专家算法在数据集上的准确度都低于90%,而BEC算法能达到超过95%的准确度。接下来与SAX-VSM[6]以及RPM[12]算法进行详细的比较和说明。在数据集中选取了几个容易混淆的活动,并把它们分成几组进行实验,分别是步行和北欧式健走、上楼梯和下楼梯、跑步和跳绳。 在步行和北欧式健走数据集上,根据训练得到的参数,BEC算法能够到达97.85%的准确度,而且只需要2.86 s的训练时间。每次实验都将观测窗口作为定值,这里的观测窗口包括窗口大小和位置,然后从原始序列中提取子序列作为SAX-VSM和RPM的数据集。如图5所示,其中(a)表示准确度比对结果,(b)表示训练时间比对结果。在对比中BEC算法只需要训练分段数据这一个参数,需要大约1 s的训练时间。但是比较完整训练时间,BEC算法也胜于对比算法所需要的3~10 s。SAX-VSM的最高准确度是95.6%,RPM的最高准确度为86.96%,而BEC算法最高能达到接近100%的准确度。 (a) (b)图5 步行和北欧健走实验结果 在上楼梯和下楼梯数据集上,BEC算法需要2.544 s的训练时间,能够达到接近100%的准确率。如图6所示,其中(a)表示准确度比对结果,(b)表示训练时间比对结果。给定序列长度,即观测窗口,SAX-VSM和RPM最高达到97.5%的准确度,但是所需训练时间很大程度上受到序列长度影响。在本例中超过800个数据点,SAX-VSM需要大约10 s的训练时间,而RPM平均需要100 s。 在跑步和跳绳数据集上,BEC算法和SAX-VSM在准确度上表现接近,都是达到了几乎100%的准确度,但是RPM无法在训练过程中处理本例中的数据量。BEC算法需要1.493 s的训练时间,但是SAX-VSM平均需要15 s的训练时间。 BEC算法在跑步和跳绳这一对比组数据上提取的特征如图7所示,图中W=55 000,N=56。(a)表示跑步原始序列,圆圈标示异常,(c)表示跳绳原始序列,圆圈标示异常,(b)、(d)分别表示跑步和跳绳的特征。从图中可见跑步由一组时间间隔和幅度接近的异常构成,而跳绳相较而言异常更加密集且凌乱。这也说明该实验者跑步步伐稳定,而跳绳较为消耗体力。 图7 跑步和跳绳对比组在时间序列正向提取的特征 5.2 在桥梁健康监测数据集上的应用 桥梁健康监测传感器收集桥梁不同位置的三个维度的加速度数据等,这里使用的是桥梁固定点Z轴加速度数据。原始数据集是一条长时间序列,以及一组时间点标记多种事件的发生。 以爆破和海浪为例,SAX-VSM和RPM的准确度分别最高为59%和86%,但是SAX-VSM需要数分钟的训练时间,而RPM需要训练超过三十分钟。由于BEC仅仅提取少量数据点作为特征,所以即使时间序列长度偏长,BEC所需的训练时间也在一分钟之内,能够达到100%的准确度。如图8所示,其中(a)表示准确度比对结果,(b)表示训练时间比对结果。 图8 爆破和海浪实验结果 本文提出了一个在现实情境下分类传感器生成的震荡时间序列的算法BEC。对于给定的长时间序列以及作为类标签的标记时间点,BEC基于DIRECT和交叉验证训练得到用于分类的合适对象,同时基于突变提取包含数值和位置信息的特征。在现实数据集上通过实验证明BEC相较于现有的算法具有更高的效率和准确性。 但是BEC算法仅仅使用固定传感器数据,而没有考虑不同位置传感器采集数据对事件识别的置信度,接下来将充分利用不同传感器提供的信息,把算法扩展为多维度的时间序列分类问题。 [1] Xing Z Z, Pei J, Keogh E. A brief survey on sequence classification[J]. SIGKDD Explorations, 2010, 12(1):40-48. [2] Ye L, Keogh E. Time series shapelets:a new primitive for data mining[C]// ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Paris, France, June 28 - July. DBLP, 2009:947-956. [3] The ucr homepage[EB/OL]. www.cs.ucr.edu/ eamonn/time series data/. [4] Hu B. Classification of streaming time series under more realistic assumptions[C]// Austin, Texas, USA.:Proceedings of the 13th SIAM International Conference on Data Mining, 2013:578-586. [5] Aggarwal C C. On effective classification of strings with wavelets[C]// Eighth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM, 2002:163-172. [6] Senin P, Malinchik S. SAX-VSM:Interpretable Time Series Classification Using SAX and Vector Space Model[C]// IEEE, International Conference on Data Mining. IEEE, 2013:1175-1180. [7] Keogh E J, Pazzani M J. A Simple Dimensionality Reduction Technique for Fast Similarity Search in Large Time Series Databases[M]// Knowledge Discovery and Data Mining. Current Issues and New Applications. Springer Berlin Heidelberg, 2000:122-133. [8] Jones D R, Perttunen C D, Stuckman B E. Lipschitzian optimization without the Lipschitz constant[J]. Journal of Optimization Theory and Applications, 1993, 79(1):157-181. [9] Vlachos M, Wu K L, Chen S K, et al. Fast Burst Correlation of Financial Data[C]// Knowledge Discovery in Databases:Pkdd 2005, European Conference on Principles and Practice of Knowledge Discovery in Databases, Porto, Portugal, October 3-7, 2005, Proceedings. DBLP, 2005:368-379. [10] Physical activity monitoring for aging people[EB/OL]. http://www.pamap.org. [11] Rakthanmanon T, Keogh E. Fast Shapelets:A Scalable Algorithm for Discovering Time Series Shapelets[C]// Austin, Texas, USA.:Proceedings of the 13th SIAM International Conference on Data Mining, 2013:668-676. [12] Wang X, Lin J, Senin P, et al. RPM:representative pattern mining for efficient time series classification[C]// Bordeaux, France:Proceedings of the 19th International Conference on Extending Database Technology, 2016:185-196. BURST-BASED EVENT CLASSIFICATION ON WEAKLY LABELED TIME SERIES DATA OF SENSORS Wang Yawen Wang Peng Wang Wei (SchoolofComputerScience,FudanUniversity,Shanghai200433,China) Detecting events on time series data generated by sensors has a great amount of attention with increasingly deployment of variable sensors. This paper proposes a novel framework for classifying events upon oscillating data of sensors called BEC. Given a long raw time series and class labels on marked time points, BEC extracts burst-based features to represent events. There are mainly two important tasks to be solved. First, BEC automatically extends labeled time points to appropriate subsequences containing sufficient information. Second, BEC extracts burst-based features to train the classification model. It is demonstrated on real-life datasets that without unrealistic assumptions and human interventions, BEC extracts burst-based features can fully detect the event, greatly retain the key information in the event, and the performance of the actual data set is better than the existing time series classification algorithm. Time series Classification Sensor data Weakly labeled 2016-02-08。中国科技部国家重点研发计划资助项目(2016YFB1000700);国家重点基础研究发展计划项目(2015CB358800);国家自然科学基金项目(61672163,61170006)。汪雅雯,硕士生,主研领域:时间序列数据挖掘。王鹏,副教授。汪卫,教授。 TP3 A 10.3969/j.issn.1000-386x.2017.07.037


4 分类和参数选取
5 实验结果及分析


6 结 语
