交通路网最优路径的搜索仿真研究
2017-08-12杨智宇
杨智宇 宗 群
(天津大学电气与自动化工程学院 天津 300072)
交通路网最优路径的搜索仿真研究
杨智宇 宗 群
(天津大学电气与自动化工程学院 天津 300072)
在道路状况日趋复杂的今天,交通路网中两点之间的最短路径已经不再是人们驾驶所需要的最优路径。传统路径规划方法存在考虑路径规划影响因素过于单一以及搜索效率过低的问题。在路径规划问题中缺少一种在多约束条件下的具体方法来实现交通路网中最优路径的高效搜索。针对上述问题,提出一种基于AHP层次分析法的改进Dijkstra算法。该算法在保有经典Dijkstra算法准确性的基础上,考虑了多种约束条件并大大提升了搜索效率。仿真结果表明,这种基于AHP层次分析法的改进Dijkstra算法具有良好的性能,能够满足当前路径规划问题的要求。
路径规划 Dijkstra算法 车联网 二叉堆 层次分析法
0 引 言
随着汽车行业的发展,以及车联网议题的提出,传统路径规划算法所得到的最短路径已经越来越不能满足当代人的需求,如何在多约束条件下来获取交通路网两点间的最优路径是当前车联网领域研究的热点问题[1]。
过去,人们在寻求最短路径时所用到的路径规划算法有很多,其中使用最为广泛也最为有效的是Dijkstra算法。在交通道路建设高速发展的今天,该算法能够很好地适应道路拓扑模型的变化、性能稳定且通用性强。但它也存在计算量上的冗余、算法效率低、运算中占用空间大等缺点。于是文献[2]首先利用桶排序将数据存储结构转换成临接表结构,然后采用矩形区域限制搜索来减少遍历结点数目;文献[3-4]提供了一种双向Dijkstra算法的策略来提高路径规划的效率;文献[5-6]对Dijkstra标号法进行了改进,并通过算法实验进行验证。文献[7]采取了一种可变搜索域的方法来减少Dijkstra算法的冗余操作并确保找到最短路径。在对经典Dijkstra算法的改进与应用中,人们往往只考虑了道路长度这一影响因素,缺少一种在多约束条件下的具体方法来实现交通路网中最优路径的高效搜索。
为了解决在多约束条件下交通路网最优路径的搜索问题,本文提出了一种基于AHP层次分析法的改进Dijkstra算法。该算法将经典Dijkstra算法和AHP层次分析法相结合,首先考虑了当代交通路网中的多种约束条件,如道路长度、道路宽度、车速限制等,设计了权重矩阵,提升了路径规划的合理性。其次,由于Dijkstra算法存在低效性等问题,将优先队列(堆)的概念引入到Dijkstra算法当中,又因为待搜索结点与起始结点连线距离小于起始结点与目的结点之间距离的结点被选取为最优路径中结点的概率极大,提出了一种基于距离限制的可变范围的结点筛选策略,减小了搜索计算的范围,大大提升了算法的效率。最后在Matlab(由于仿真平台使用Matlab,故本文中编程指令和语法均以Matlab中的指令和语法为准)中对改进的算法进行了实验验证,证明了算法的有效性。
1 交通路网路径规划原理
在对交通路网进行路径规划时,首先会把路与路之间的拓扑关系以图G=(V,E)的形式存储起来[8],其中V和E是两个集合,前者是图G中顶点的有限非空集合。后者称之为顶点之间关系的集合,也就是边的集合。V和E的表达方式如式(1)、式(2)所示:
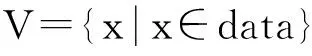
(1)
E={VE}
(2)
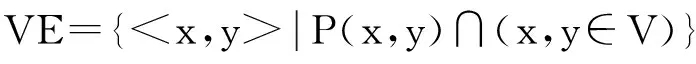
(3)
式(3)是对边集合E的一个解释,其中P(x,y)表示顶点x与y之间存在的路径。在这里,V中的每一个顶点代表着地图相应的路口结点并存储该路口的位置信息。E中的每一条边代表着与其连接的两个路口结点之间的权值。
于是复杂的交通路网就可以简化为图1的形式。
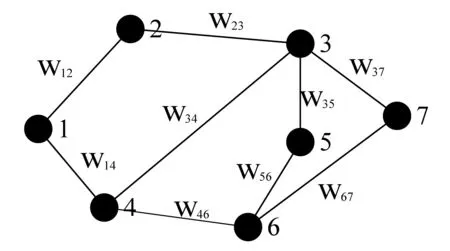
图1 交通路网道路拓扑关系图
于是结点和边之间的关系就可以用邻接矩阵A=(aij)n×n来存放。其中aij如式(4)所示:
(4)
式中,i,j=1,2,…,n;wij是结点Vi和结点Vj之间的权值,如果两个结点不相连则用inf表示。故图1所示的交通路网模型所对应的邻接矩阵如式(5)所示。
(5)
随着现代社会的发展,交通线路变化越来越快,具有良好适应性Dijkstra算法也越来越受到重视[9]。经典Dijkstra算法采用遍历搜索所有节点的方式来完成最优路径的获取,即从起始结点开始,计算出所有结点与起始结点之间的权值,并通过比较找到最小权值的结点。将此结点标记并记录该结点的信息(被标记过的结点之后不再参与搜索),然后将该结点作为新的起始结点。重复上述步骤,直到找到目的结点为止,最终记录得到的途径结点集合就是所需要的最优路径[10]。
在传统路径规划方法中,两路口结点之间的权值通常为两路口之间的距离。因此通过传统权值邻接矩阵所得到的最优路径即为最短路径,但随着现代交通的发展,影响路径规划的因素越来越多,如道路长度,车道数目,车辆密度等。并且随着交通线路越来越多、越来越复杂、遍历式搜索的Dijkstra算法需要搜索大量的无关结点,计算的冗余性大大降低了路径规划的效率[11-12]。于是这种考虑影响因素单一、低效的路径规划方法越来越不能满足路径规划的需求。
综上所述,在路径规划问题中构建一个考虑了多种影响因素的权值邻接矩阵成为了获得良好路径的前提,再根据优先队列的特点以及待搜索结点与起始结点连线距离小于起始结点与目的结点之间距离的结点被选取为最优路径中结点的概率极大的特性,将Dijkstra算法进行改进。改进的Dijkstra算法使得单次搜索效率以及获得最优路径的质量显著提升。这样利用改进的Dijkstra算法所搜索到的最优路径能够更好地满足路径规划的需求。
2 基于AHP层次分析法的改进Dijkstra算法
2.1AHP层次分析法
2.1.1 多约束条件权重的获取
AHP层次分析法是美国运筹学家萨迪教授提出的,该方法在赋权的过程中能够充分利用专家的经验,并具有较广的适用范围[13]。在存在多约束条件的路网模型中,AHP层次分析法能够设计出一种满足用户需求的权重矩阵。
采用层次分析法确定权重矩阵的步骤如下所示。
(1) 建立递阶层次结构模型
在交通路网中,对车辆行驶的约束条件有许多,按照车辆行驶的实际情况并根据层次分析思想建立了影响道路权值的层次结构模型。如图2所示。
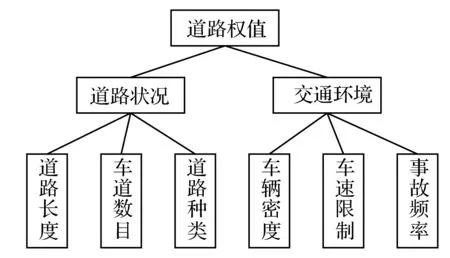
图2 道路权值的层次结构
(2) 构造两两比较判断矩阵
专家参照表1对指标体系各个层次的元素进行评价意见,得出两两判断矩阵A,并根据式(6)从判断矩阵中计算出每个指标相对于上一层元素的相对权重。
AW=λmaxW
(6)
其中W是特征向量,将其归一化处理后得出相应指标权重。

表1 1- 9标度的含义
(3) 一致性判断

若C.R.<0.1,则认为判断矩阵满足一致性要求。表2为最终求得的影响道路权值的各项指标所占的权重。

表2 影响道路权值的指标及其权重
2.1.2 多约束条件的整合
在得到了不同约束条件的影响权重后,我们需要将不同约束条件整合在一起。首先我们将不同约束条件分为成本型和效益型,对每个约束条件设其取值范围为ui=(ai,bi),当约束条件为成本型时,根据式(7)进行量化,当约束条件为效益型时,根据式(8)进行量化。
(7)
(8)
我们将得到的权重以及该约束条件量化后的结果通过式(9)进行计算,以W作为道路的权值,并以此来构建路径规划问题中的邻接矩阵。
W=ω1×g1+ω2×g2+…+ω6×g6
(9)
2.2Dijkstra算法的改进
2.2.1 优先队列
在Dijkstra算法中,最消耗时间的一个步骤就是在未标记的结点集合中找到距当前结点距离最小的那个结点(下文称为最小结点),然后更新距离矩阵。如果不采取任何排序策略,在数据量较大的情况下,这将严重影响算法的执行速度。而Dijkstra算法的这种运算策略恰恰与优先队列这种数据结构的特点相符,找到最小结点并标记的步骤恰恰与优先队列的deleteMin(删除最小者)操作相似。
本文采用二叉堆对优先队列进行具体实现。二叉堆具有两个性质,即结构性和堆序性,因为我们需要寻找的是最小结点,所以在构建二叉堆时将最小结点放在根结点处,这使得Dijkstra算法在进行最小结点搜索的时候只需要提取根结点就能够得到满足要求的结点,再令剩余的结点保持堆序性形成一个新的最小二叉堆,重复这个过程即可满足算法的需要。在这个过程中我们不仅得到了最小结点,还省去了经典Dijkstra算法中标记结点的工作,因为最小结点已经自动在最小二叉堆中删除。堆结构的另一个优点是我们只需用一个一维数组就能够实现堆,从而实现对交通路网中待搜索结点的存储。通常二叉堆数组中任意位置i上的元素,其位置2i上为其左儿子,位置2i+1上为其右儿子,其父结点则在i/2位置上,而在本文所构建的二叉堆数组中还将在其第n+1个位置上存放堆结点的数目。
用一个例子来说明本文中最小二叉堆的数组表示方法,每个结点对应的值如表3所示。其数组实现如图3所示。

表3 结点数值表

3521764712345678
图3 二叉堆的数组实现
2.2.2 结点的筛选
Dijkstra算法是一种贪婪算法,它会以起点为圆心向外发散式的搜索结点。在实际操作中,经典Dijkstra算法可能会遍历图中的任意结点,即使该结点距离起点非常远,显然这将消耗大量的时间和资源并且是无意义的。而文献[3]双向Dijkstra算法从两端同时向中间搜索结点,理想情况下能够减少近50%的搜索结点的数目,但是当结点数目达到一定规模的时候,从起始结点和目的结点之间有许多不同的路径,在最坏的情况下双向搜索会是单向搜索工作量的两倍,故双向Dijkstra算法并没有看上去那么高的搜索效率。并且当搜索迭代次数需要进行成百上千次乃至更高时,通过复杂计算筛选结点的方式反而会增加路径规划算法的时间。
本文根据现代交通路网的特点:待搜索结点与起始结点连线距离小于起始结点与目的结点之间距离的结点被选取为最优路径中结点的概率极大,提出了一种基于距离限制的可变范围的结点筛选策略,进一步改进了Dijkstra算法的效率,提升了算法质量。我们通过确定起点s的坐标(x1,y1),和终点e的坐标(x2,y2),然后通过式(10),求得优先搜索范围的半径。
(10)
当搜索结点不在本文所设定的圆形搜索范围内时,我们将该结点“抛弃”使其不在优先搜索结点的范围之中,伪代码如下所示:
DISTANCELIMIT(G, s ,e , n)
1 Q←?
2 R←DISTANCE(s ,e , n)
//确定搜索范围半径
3.for each vertex v∈V[G]
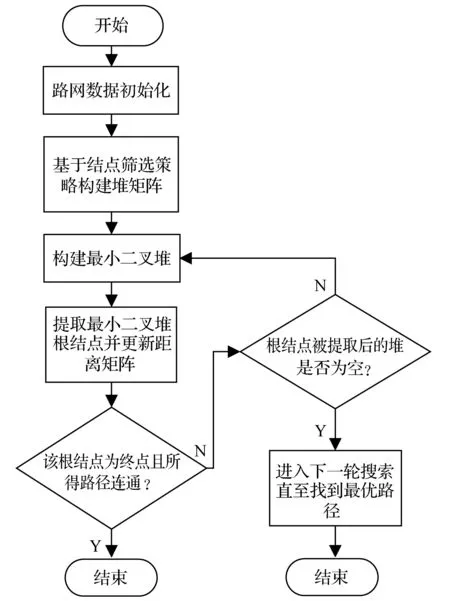
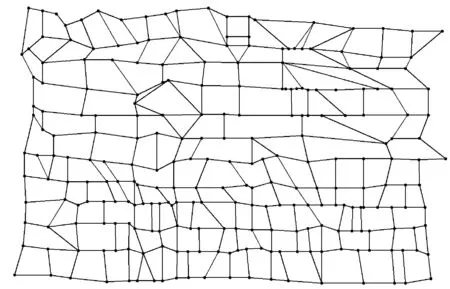
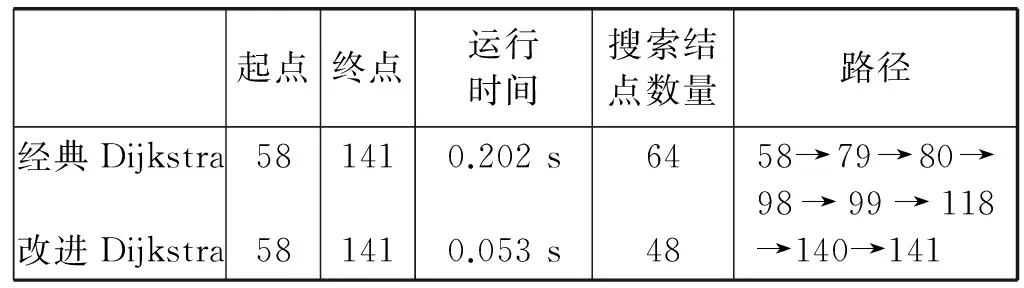
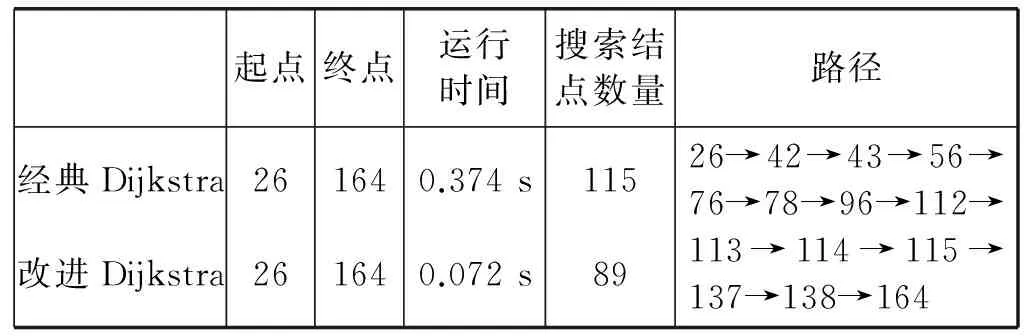
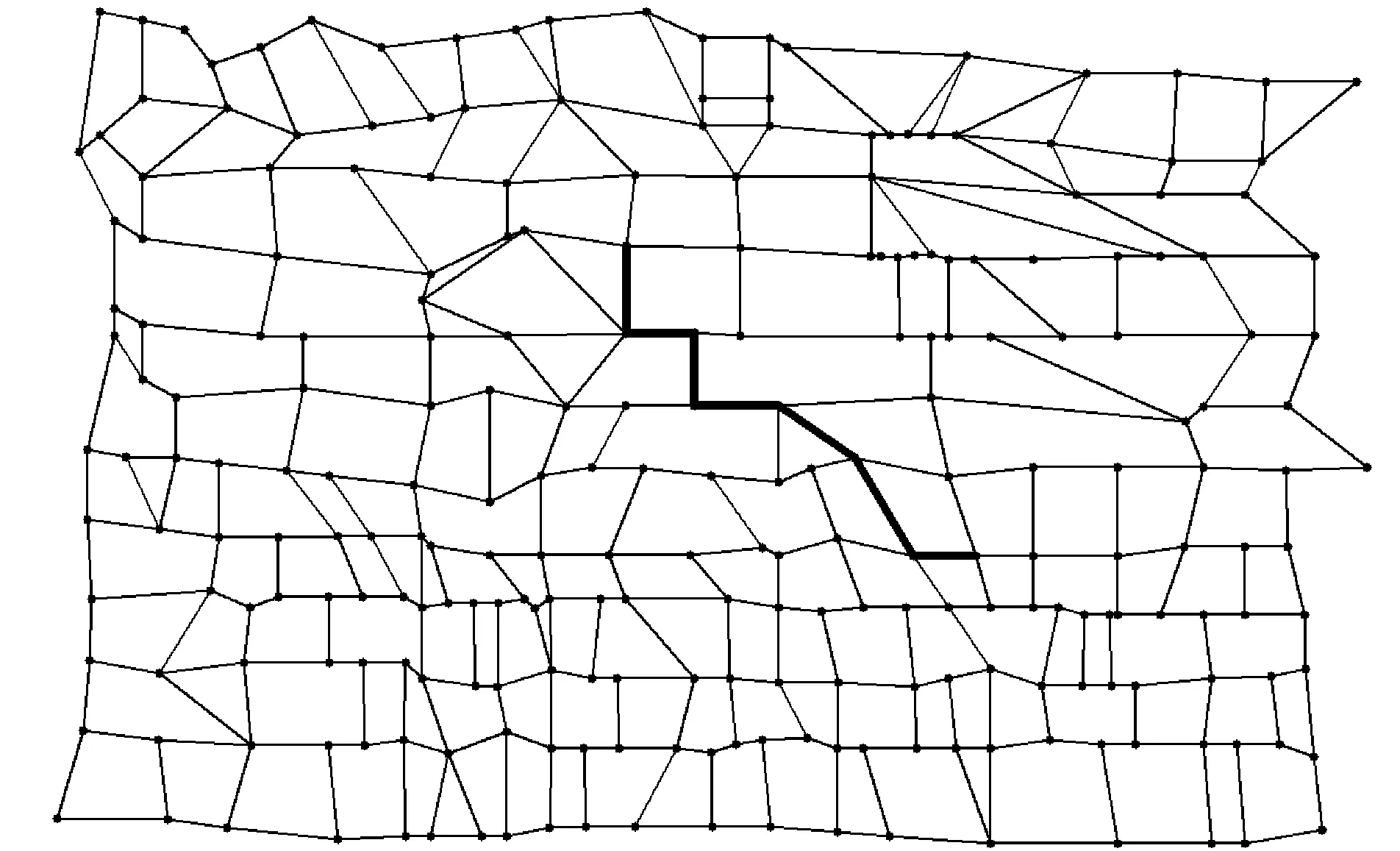
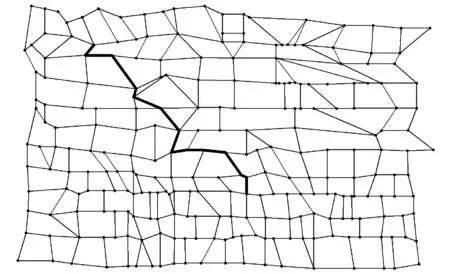
4 IF DISTANCE(s ,v) 5 Q←Q∪{v} 因为在交通路网中两点之间一定是可达的,为了避免在结点筛选过程中丢失重要路径,从而出现改进Dijkstra算法无法搜索到最优路径的情况,本文使用的距离限制方法是一种可变范围的结点筛选策略。我们在式(10)中引入一个常数项C和一个变量n,当改进Dijkstra算法没有找到最优路径时,我们将变量n按梯度增加,从而扩大改进Dijkstra算法的搜索范围,使其覆盖范围包括更多数目的结点,再进行搜索。如此反复,直至改进Dijkstra算法在交通路网中发现最优路径为止。 如图4所示,在使用结点筛选策略以前改进Dijkstra算法需要对全图的结点进行搜索运算,即使该结点已经远远偏离目的结点,根本不可能成为最优路径中的一员。在引入基于距离限制的可变范围的结点筛选策略以后,我们将搜索范围牢牢控制在本文所规定的圆形范围之内,这使得我们需要进行搜索的结点数目大大减少,并且搜索结点的位置更加集中,不会出现搜索远距离偏移的现象,提高了搜索的效率和质量。一旦在规定的范围内没有搜索到最优路径,那么算法就会自动进入到下一轮搜索之中,扩大搜索范围直至发现最优路径。通过实验验证,本文所设计的基于距离限制的可变范围的结点筛选策略能够满足交通路网的需求,最终找到最优路径。 图4 改进Dijkstra算法使用可变范围的结点筛选策略搜索最优路径 综上所述,改进Dijkstra算法在交通路网中搜索最优路径的流程如图5所示。 图5 改进Dijkstra算法搜索最优路径的流程图 为了验证改进后算法的性能,在Matlab中设计仿真实验进行验证。首先在Matlab中读取矢量电子地图的图形数据,然后在Matlab中构建矢量电子地图,如图6所示。我们先在仅考虑道路长度的情况下使用改进Dijkstra算法和经典Dijkstra算法对起点为58号结点,终点为141号结点以及起点为26号结点,终点为164号结点的两条路径进行搜索,在表4和表5中记录运行时间、搜索结点数等相关实验数据和结果。 图6 交通路网模型 起点终点运行时间搜索结点数量路径经典Dijkstra改进Dijkstra58581411410.202s0.053s644858→79→80→98→99→118→140→141 表5 实验结果对比表2 在表4和表5的对比分析中可知,改进Dijkstra算法在运行时间上明显少于经典Dijkstra算法,这不仅仅是因为改进Dijkstra算法搜索的结点数目偏少,还因为改进Dijkstra算法的。 对于图7所示的实验而言,经典Dijkstra算法在252个节点中搜索了64次确定了最优路径58→79→80→98→99→118→140→141;改进Dijkstra算法经筛选后确定了更加精确的结点范围,确定最优路径在其中126个结点之间,随后在126个节点中搜索了48次确定了最优路径58→79→80→98→99→118→140→141。 对于图8所示的实验而言,经典Dijkstra算法在252个节点中搜索了115次确定了最优路径26→42→43→56→76→78→96→112→113→114→115→137→138→164,而改进Dijkstra算法则在147个节点中搜索了89次确定了同样的路径。 图7和图8中的粗线为标记出的此次算法实验所获得最优路径。 图7 起点为58、终点为141的路线 图8 起点为26、终点为164的路线 单次搜索效率要明显优于经典Dijkstra算法。因此可以看出,改进Dijkstra算法在路径规化效率上有了很大的提高。两次实验所搜索到的最优路径是一致的,故改进Dijkstra算法在提升工作效率的同时并没有破坏其路径规划的准确性。并且通过这两组实验数据我们还可以发现,使用结点筛选策略处理后的Dijkstra算法的搜索区域明显减小,这一特点将随着路网复杂程度的增加有着明显的提高;并且搜索的路径越短,搜索结点的范围越精确,故该算法更适合短距离搜索或城市内部搜索,恰恰适用于在城市车联网中应用。 我们再在多种约束条件的情况下使用改进Dijkstra算法对起点为58号结点和终点为141号结点进行路径搜索,得到如图9所示的路线图。 图9 多约束条件下起点为58、终点为141的最优路线 在考虑了多种约束条件带来的影响以后,我们所得到的路线为58→79→80→81→82→100→119→141,该路线和图7所示的路线有着些许的不同,但是不难发现图9所显示的路线更加平滑、连贯。此时虽然所得到的路径不是最短路径,但是在可以接受的范围内,并且更加符合当代人的驾驶习惯、道路质量明显优于图7所示的道路质量,故该路径应为最优路径。 综上所述,在考虑多种约束条件的影响下,改进Dijkstra算法不仅缩小了搜索区域,提升了搜索线路的效率和质量。还通过引入二叉堆使得单次搜索需要耗费的时间大大减少,这也是改进Dijkstra算法效率显著提升的重要原因之一。 Dijkstra算法是路径规划领域得到广泛应用的一种算法。本文提出一种基于AHP层次分析法的改进Dijkstra算法。将二叉堆引入到经典Dijkstra算法当中,又结合对现代路网特性的考虑,提出了基于距离限制的可变范围的结点筛选策略来缩小搜索区域,节省了存储空间,减少了搜索次数,提高了搜索效率,使得算法的性能得到了全面提升。并在考虑多种约束条件的情况下,构建权重邻接矩阵,使得算法所得到的路径更加合理,更加符合当代人的驾驶习惯。实验表明,基于AHP层次分析法的改进Dijkstra算法能够有效地在矢量电子地图中找到最优路径并标记出来,并且该算法独有的特性更加适用于在城市车联网中应用,具有良好的使用价值。 [1] Bast H, Delling D, Goldberg A, et al. Route Planning in Transportation Networks[J]. Microsoft Research, 2015. [2] 沈国杰. 车载导航系统的最优路径规划算法研究[D]. 大连理工大学, 2013. [3] 李杰, 张文栋, 杨卫. 双向Dijkstra算法设计与实现[C]// 中国宇航学会深空探测技术专业委员会学术年会. 2007. [4] Yin C, Wang H. Developed Dijkstra shortest path search algorithm and simulation[C]// Computer Design and Applications (ICCDA), 2010 International Conference on. IEEE, 2010:V1-116 - V1-119. [5] 王树西, 吴政学. 改进的Dijkstra最短路径算法及其应用研究[J]. 计算机科学, 2012, 39(5):223-228. [6] 杨柳. 车载导航系统中路径规划算法的研究及实现[D].北京交通大学, 2008. [7] Wang S X, Zhao X Q. The improved Dijkstra's shortest path algorithm[C]// Natural Computation (ICNC), 2011 Seventh International Conference on. IEEE, 2011:2313-2316. [8] 郁晓慧. 基于智能终端的车载导航路径规划的研究[D]. 东华大学,2015. [9] Kang H I, Lee B, Kim K. Path Planning Algorithm Using the Particle Swarm Optimization and the Improved Dijkstra Algorithm[C]// The Workshop on Computational Intelligence & Industrial Application. IEEE Computer Society, 2008:1002-1004. [10] 林青岩. 智能交通中车辆最优路径规划策略研究[D].吉林大学,2013. [11] Zhang F, Liu J. An Algorithm of Shortest Path Based on Dijkstra for Huge Data.[C]// Fuzzy Systems and Knowledge Discovery, Fourth International Conference on. IEEE, 2009:244-247. [12] Xiao J X, Lu F L. An improvement of the shortest path algorithm based on Dijkstra algorithm[C]// Computer and Automation Engineering (ICCAE), 2010 The 2nd International Conference on. IEEE, 2010:383-385. [13] Zhi-Jun S U, Yan H. Research on the Feasibility Evaluation of Helicopter Route Based on GIS and AHP[J]. Surveying & Mapping of Geology & Mineral Resources, 2013. RESEARCH ON SIMULATION OF OPTIMAL PATH OF TRAFFIC NETWORK Yang Zhiyu Zong Qun (SchoolofAutomationandElectricalEngineering,TianjinUniversity,Tianjin300072,China) In the increasingly complex road conditions today, the shortest path between two points in the traffic network is no longer the optimal path that people need to drive. The traditional path planning method has the problem that the factors of path planning are too single and the search efficiency is too low. In the path planning problem, there is a lack of a specific method in the multi-constraint conditions to achieve the optimal search path in the traffic network. Aiming at these problems, an improved Dijkstra algorithm based on analytic hierarchy process (AHP) is proposed. Based on the accuracy of the classical Dijkstra algorithm, the algorithm considers various constraints and greatly improves the search efficiency. The simulation results show that the improved Dijkstra algorithm based on AHP has good performance and can meet the requirements of current path planning problems. Route planning Dijkstra algorithm Internet of vehicles Binary heap AHP 2016-05-12。国家自然科学基金面上项目(61273092)。杨智宇,硕士生,主研领域:车联网,无人驾驶。宗群,教授。 TP368.1 A 10.3969/j.issn.1000-386x.2017.07.004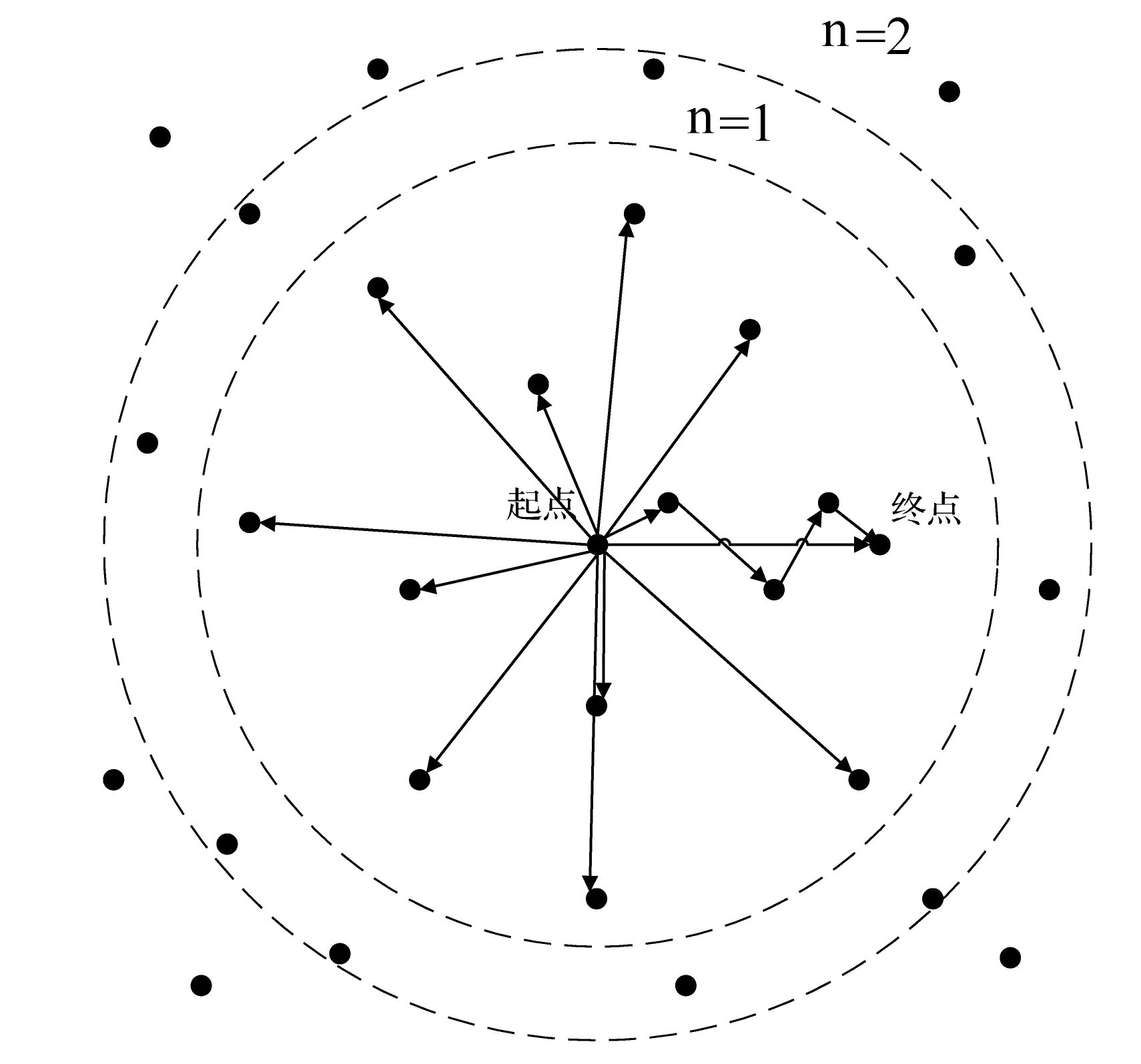
3 仿真结果与分析
4 结 语
