卫星终端分布式相控阵天线时延估计方案

马春阳，李 健，罗 勇，程宇新，吴建军

(北京大学 信息科学技术学院 现代通信研究所，北京 100871)



卫星终端分布式相控阵天线时延估计方案

马春阳，李 健，罗 勇，程宇新，吴建军

(北京大学 信息科学技术学院 现代通信研究所，北京 100871)

针对卫星终端分布式相控阵天线系统的传统时延估计方案存在的问题，研究了基于合成信号的多路时延估计方案，设计了简化方案的动态调整策略，仿真结果表明该方案能够有效地提升时延估计的性能，算法复杂度较低，同时添加动态策略的时延估计简化方案能较好地减小系统误差。

分布式相控阵天线；时延估计；合成信号；动态调整

0 引言

在卫星移动通信系统中，卫星终端分布式相控阵天线系统需要在上行链路和下行链路的接收端将接收到的多路天线信号进行加权叠加，以提高信号的质量。但由于多个天线在终端载体分布的空间位置不同，信号在到达接收端时经历的时延也不相同，因此需要将多路信号在时间上进行对齐。

依照待估时延的信号路数进行分类，时延估计算法可以分为两路时延差估计方案和多路时延差估计方案[1]。对于两路信号的时延差估计方案，最经典的方法为基于互相关的时延差估计方法。该方法将两路信号进行互相关运算，在相关运算的过程中信号将进行相对移位，互相关结果的最大值对应着两路信号最大的相似程度，信号间对应的相对移位即对应信号的时延差估计值[2]。与之不同，基于 LMS 的自适应时延差估计方案将待估的两路信号分别作为自适应系统的参考信号和基本输入，通过迭代算法使得两路信号之间的差异达到最小[3]。

在多天线信号模型下，现有的完全联合多路时延估计算法有：特征值分解法、多通道互相关法、冗余融合算法以及盲信道辨识法[4]。

特征值分解法是以矩阵特征分解理论为基础的空间谱估计，它的优点在于时延估计的分辨率精度比较好，缺点在于矩阵的运算带来较大的运算量，对于频谱不平坦的信号性能下降明显，并且只适用于天线位置已知的场景[5-6]。

多通道互相关法利用多天线信号间的时域和空域冗余信息来进行时延差的估计，提取出有用的部分降低算法在多路情况下对噪声的敏感度，使得在信噪比较低的情况下仍保持较好的性能[7-9]。与特征值分解法一样，这类算法需要事先知道天线的位置信息，把多路信号时延估计转化为单路信号时延估计。

在 LMS 自适应时延估计算法的基础上，为了进一步提高复杂信道环境下时延估计的性能，文献[10-11]提出了自适应特征值分解算法，该算法将信道的影响等效成冲激响应滤波器对信号的滤波过程，并利用冲激响应的峰值估计出时差，本质上是盲信道辨识算法。此外，该算法存在对噪声敏感、计算量大以及稳健性差等缺点，在实际系统中难以应用。

1 信号模型

分布式天线技术是指利用分布在终端的多个天线组成的阵列对信号进行联合的发送和接收，并对接收到的信号进行有效合成以提高信号的质量。由于天线分布在终端的不同空间位置，它们发送和接收的信号经过不同的信道，造成各路信号在下行链路到达卫星地球终端或是上行链路到达星上时，由于电磁波传播距离不同而存在一定的时延差异。对于频率较高的信号来说，它们的信号波长较短甚至在毫米级别，很小的时间差即可对信号的合成造成较大的影响。为了研究信号的时延对齐方案，首先建立分布式相控阵天线的信号处理模型。

卫星终端分布式相控阵天线的信号传输示意图如图1所示，天线分布在卫星终端载体的不同空间位置、不同天线之间的空间距离为Di。以天线2为例，假设已知其对准卫星时波束的入射角θ，根据图中的几何关系，可以大概估算出信号到达不同天线时的传输时延差。

τi≈(Dicosθ)/v。

(1)

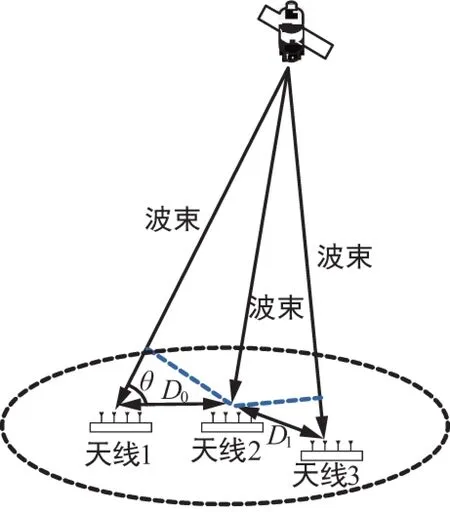
图1 信号时延差异示意图

另外，由于分布式天线的发送和接收设备之间存在不一致性以及多路信号信道之间的差异，各路信号之间还存在一定的相位差，信号的信噪比也不尽相同。因此建立卫星终端分布式相控阵天线的信号模型如下，设第i(i=1,2,···N)路的信号模型为：

xi(t)=ais(t-τi)ej2πf(t-τi)+jθi+ni(t) ，

(2)

式中，ai为该路信号的幅值大小，由于每个相控阵天线阵列的波束相对卫星的指向不同，不同天线接收到的信号幅度可能存在较大差异。τi为该路信号的时延延迟，θi为该路信号的附加相位，f为信号的载波频率，这里假设不同天线的信号之间不存在频率偏差，ni(t)为噪声，分布式天线信号间的噪声均为零均值的高斯白噪声，且噪声之间不存在相关性。

2 分布式天线时延估计方案

2.1 2种传统时延差估计方案

由信号的合成原理可知，信号的加权合成可以有效提高信号的质量，合成信号的信噪比将大于其中任何一路信号。因此，对于分布式相控阵天线系统，可以考虑将多路信号的加权合成作为参考信号，分别与所有路信号进行2路时延估计，以提高多天线信号时延估计的精度。将文献[12]提出的基于多个参考信号的时延差估计记为方案一，基于合成信号的改进多天线自适应时差估计方案记为方案二，其原理分别如图2和图3所示。

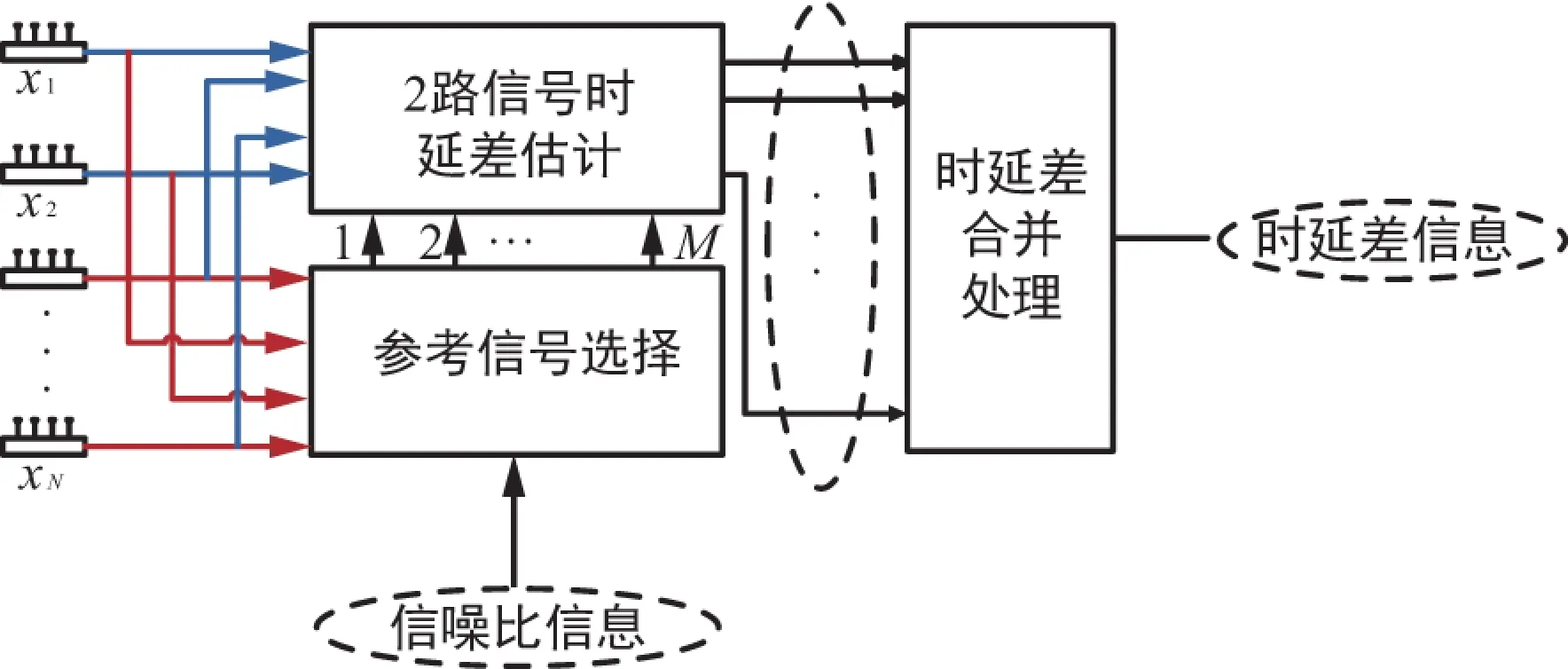
图2 分布式天线时延对齐方案一原理图

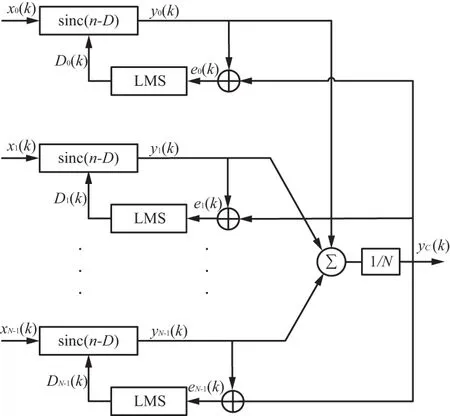
图3 分布式天线时延对齐方案二原理图

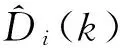
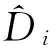
(3)

2.2 动态调整的简化时延差估计方案

上述时延估计方案利用下行链路收到的多路信号进行信号处理，得到分布式天线之间信号的时延差异并对时延进行补偿。这种方案需要将接收到的多路信号连续地送入时延估计模块以进行准确的时延对齐，对于系统来说会带来较大的开销。因此，可以考虑在分布式天线系统中对信号时延对齐的过程进行简化。

一种可行的思路是系统减少对时延估计的次数，即在一定时间周期内分布式天线系统利用估计出的历史时延差值作为信号时延调整的依据，直接对本次信号进行相应的时间调整。对于此种简化方案，当终端移动速度较快时，卫星终端分布式天线之间信号的传输路径会发生较大的变化，信号间的时延差值也会发生较大的变化，单纯通过减少时间估计次数将历史时延差值作为本次时间调整的依据，会带来较大的误差从而造成系统性能的下降。因此，需要采取一定的时延差动态调整策略以进行时延误差的补偿。

卫星终端移动过程中分布式天线间路程差变化的几何结构示意图如图4所示。

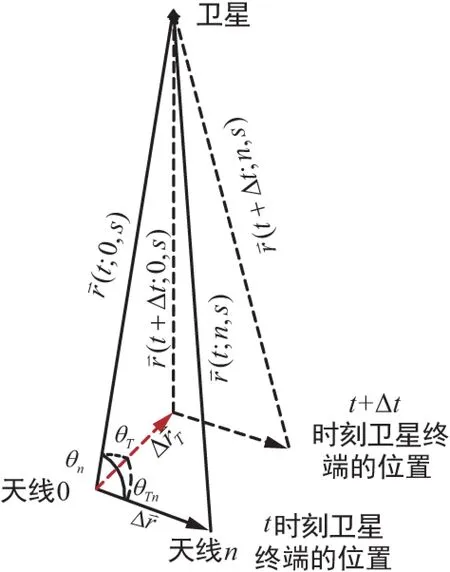
图4 卫星终端移动过程几何关系示意图

不同地球站和卫星在不同位置距离差的变化值，整理后可以表示为：

Δdn(t,Δt)=[dn(t+Δt)-dn(t)]-

[d0(t+Δt)-d0(t)]=[dn(t+Δt)-d0(t+Δt)]-

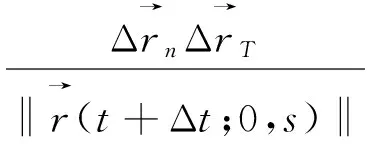
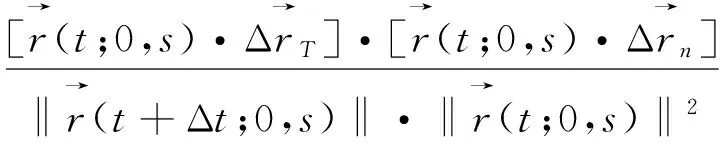
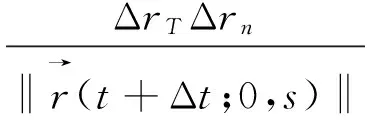
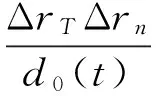
(4)

如果在某一时刻已知分布式天线之间的距离，卫星相对于终端的方位角和俯仰角，以及卫星终端的运动方向，通过空间几何关系进行建模计算，可以得到θTn、θT、θn等角度，假设终端移动的速度为v，时延估计周期为Δt，即可得到ΔrT，由此可求得此周期内卫星相对于不同天线之间距离差的改变，根据Δτ=Δd/c可以得到本次发送时刻与时延估计时刻相比需要调整的时延差，其中c为电磁波传播的速度。

3 仿真分析

假设卫星终端分布式相控阵天线的个数为10，信号采用QPSK调制，各路信号的噪声为零均值额高斯白噪声，且噪声之间相互独立，迭代步长μ设为0.05，信号的延迟为[-5Ts，5Ts]。

3.1 2种传统时延差估计方案的时延估计性能对比

对第2路信号的时延差估计结果τ12进行统计，方案一和方案二的仿真结果如图5和图6所示。从图5中可以看出基于合成信号的多路自适应时延估计算法在迭代一定次数以后可以达到收敛的状态，证明了其收敛性和可行性。图6的时延估计误差结果表明，方案二的时延估计误差性能优于方案一，与理论分析相吻合。说明在分布式天线系统中采用合成信号作为时延差估计的参考信号，可以带来时延估计性能的提升。

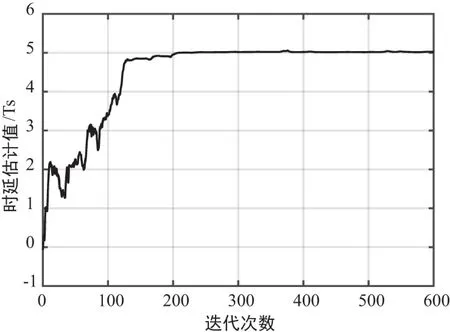
图5 收敛性仿真

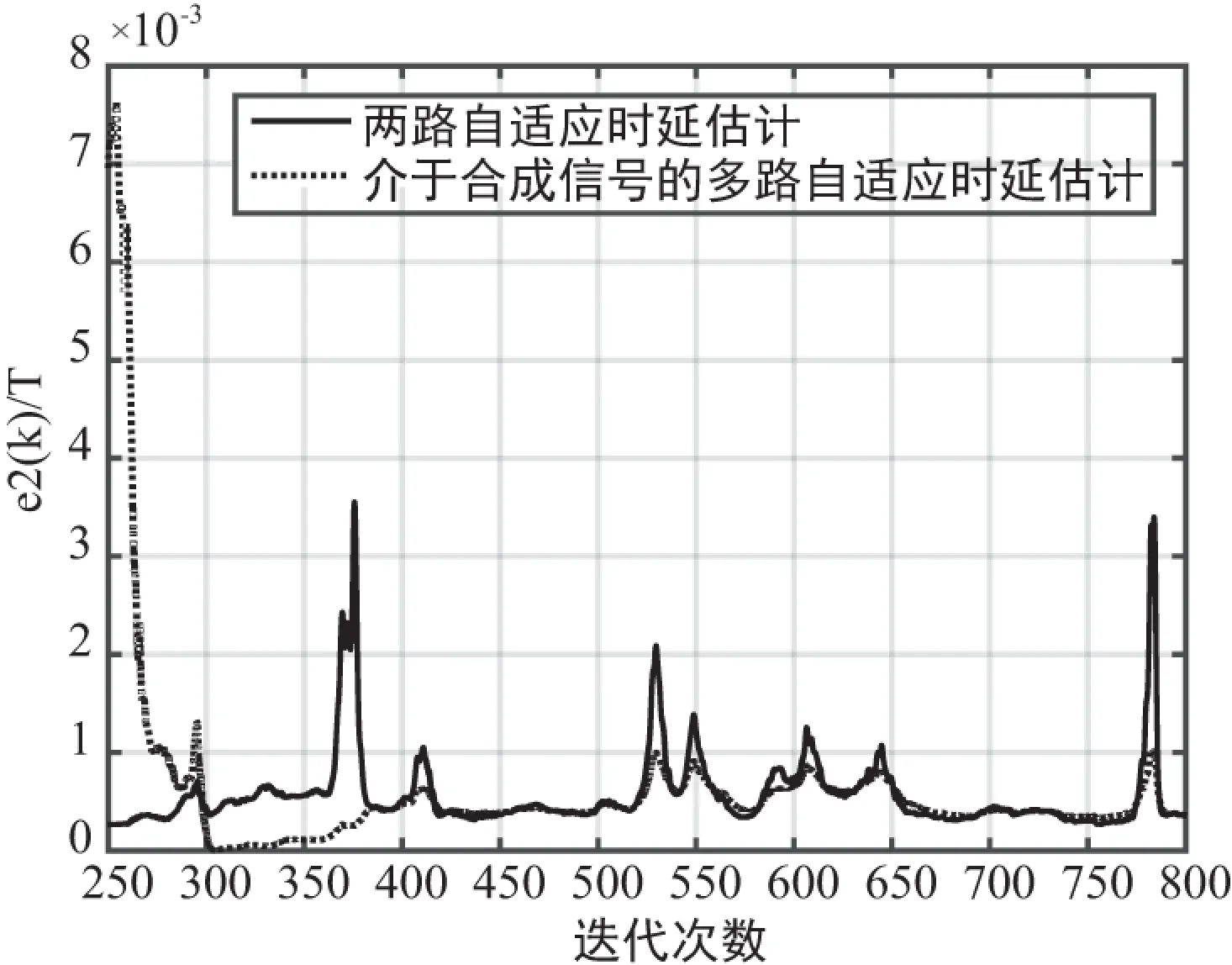
图6 时延估计误差

设共有10路天线，它们的信噪比依次是Eb/N0+[10 dB,9 dB,8 dB,…,1 dB]，对时延估计方案中的τ14进行统计，其仿真结果如图7和图8所示。从仿真结果可以看出，由于方案一采用的迭代算法是基于2路确定信号的自适应时延差估计，方案二采用的迭代算法基于不固定的合成信号，故方案一的收敛速度略快于方案二；但从时延估计的精度来看，方案二的归一化均方误差小于采用2路自适应时延估计的误差，能够带来一定程度的性能提升，同时不会对算法的复杂度带来过多的影响。

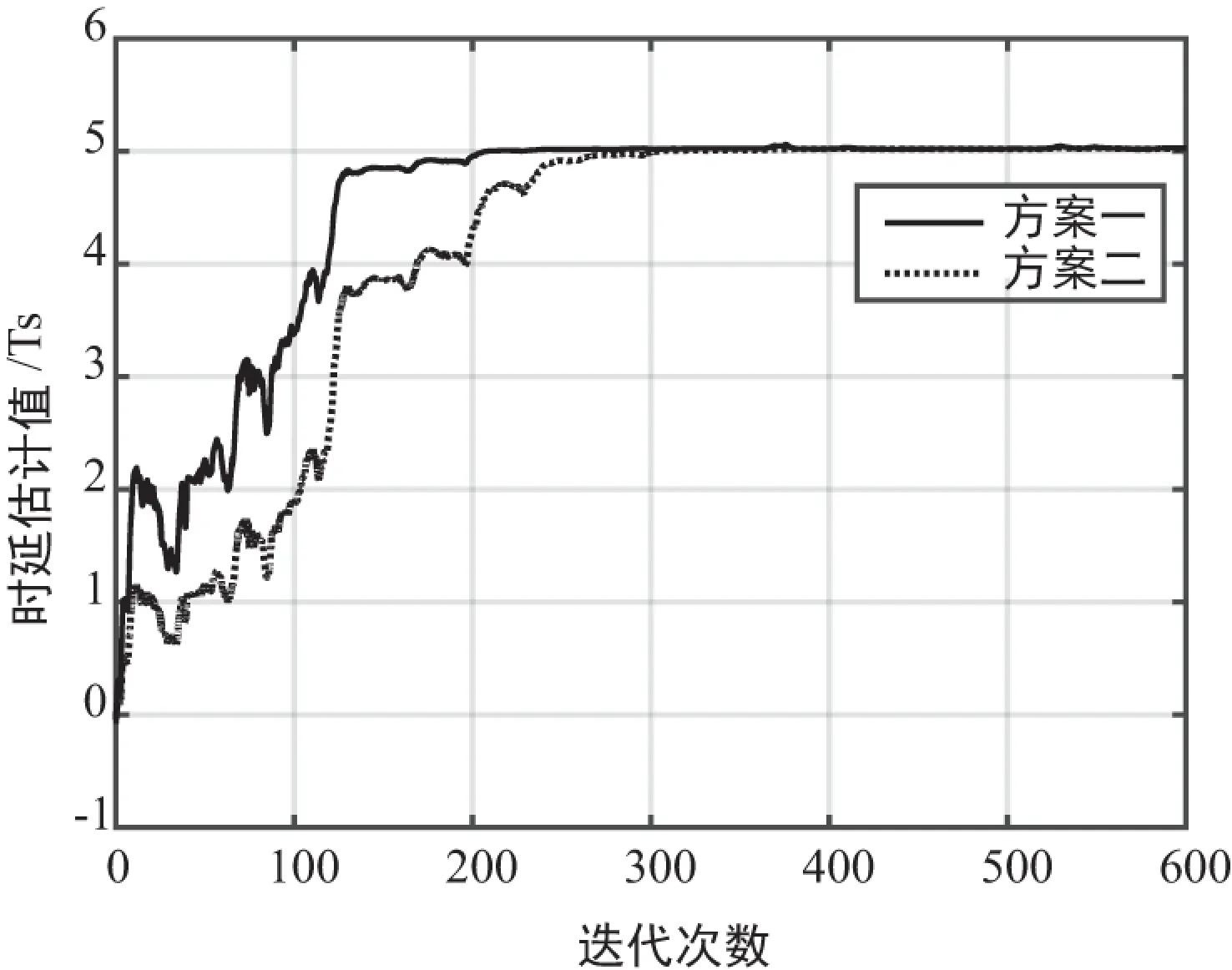
图7 收敛性对比

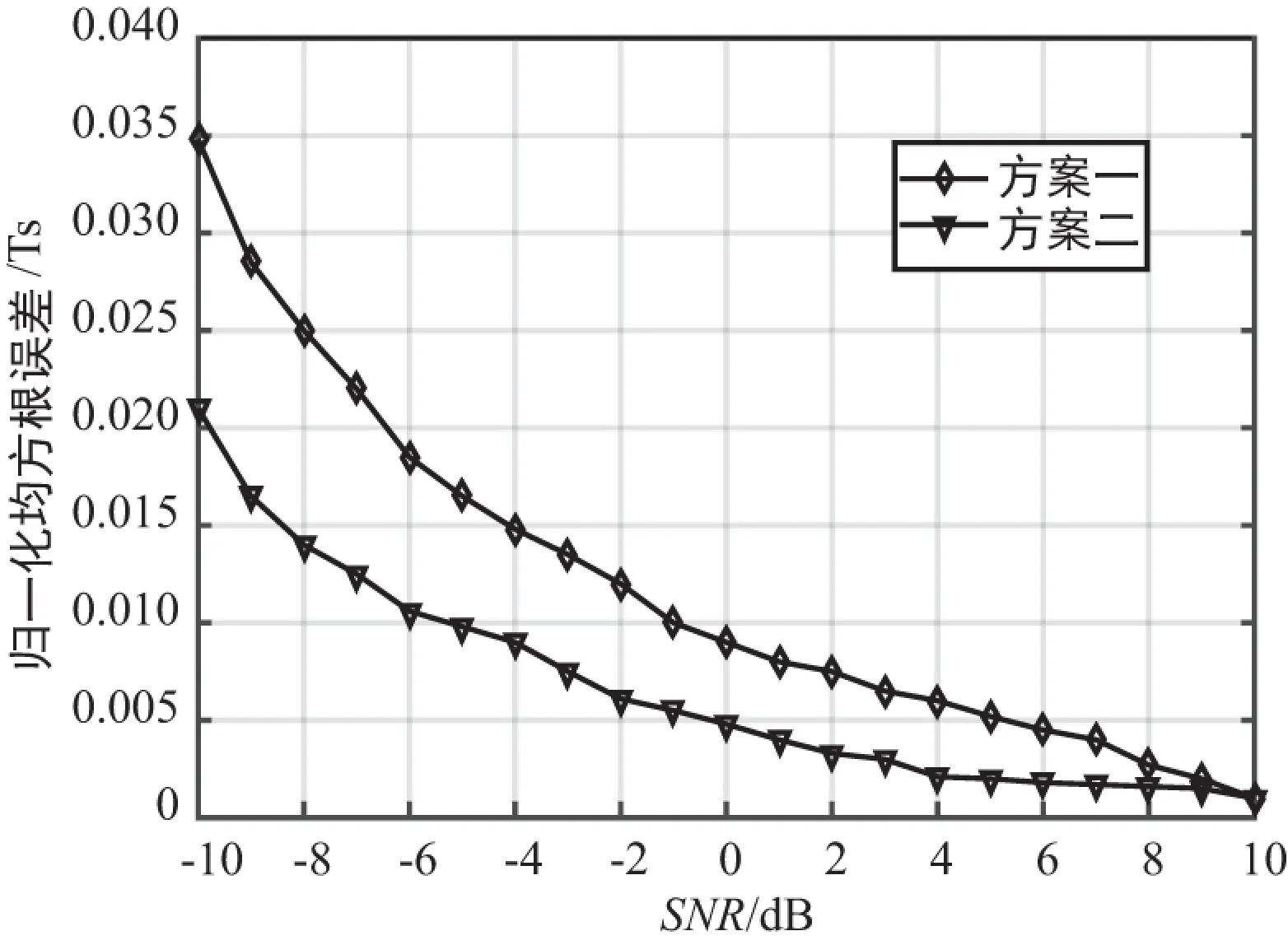
图8 时延估计性能对比

3.2 动态调整的简化时延差估计方案性能比较

假设终端移动速度为1 000 km/h，2个天线之间的间隔为50 m，将2次时延估计间的周期设为100 s，采用时延调整策略与未采用时延调整策略时2路信号间的时延误差如图9所示。

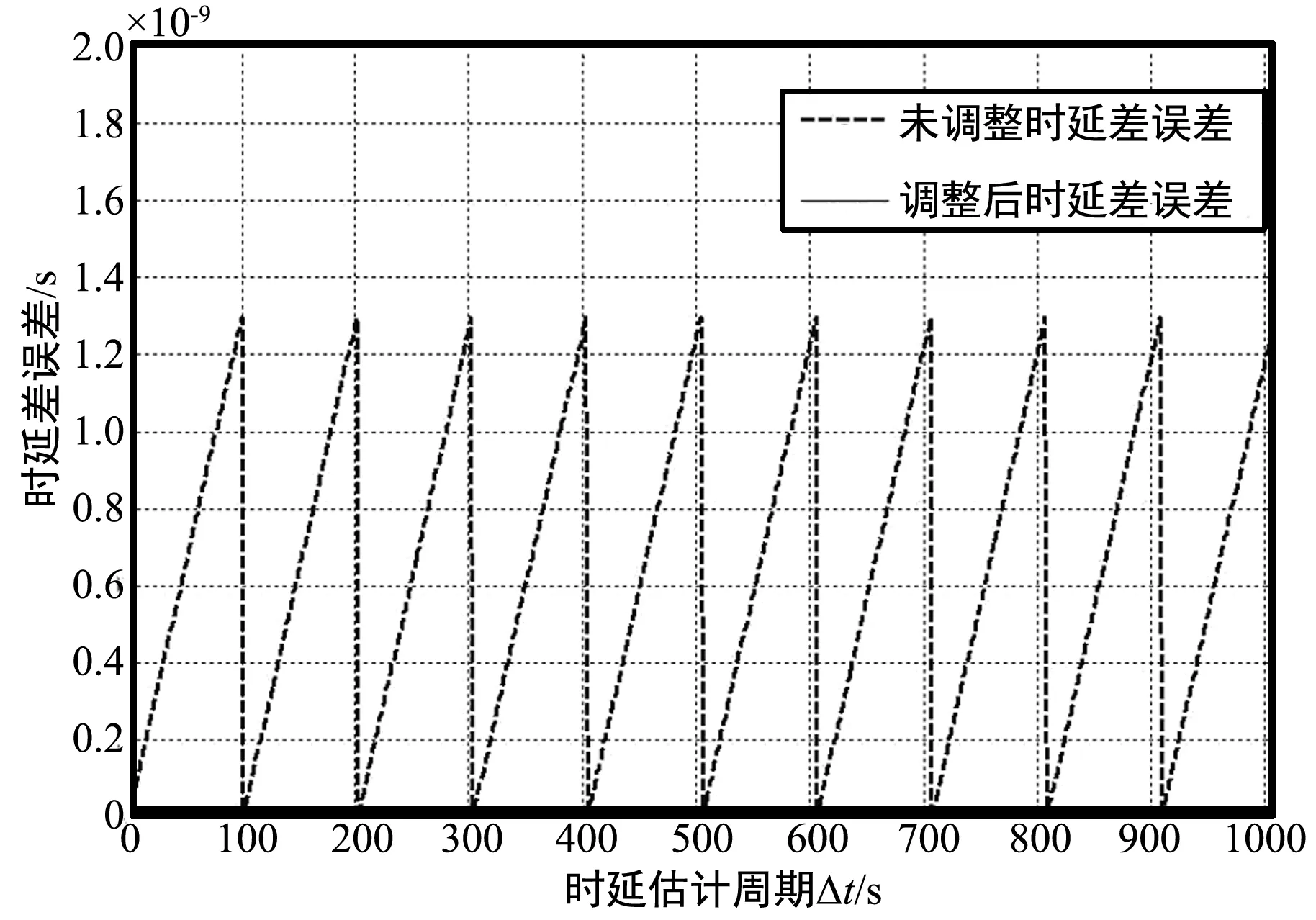
图9 时延误差变化曲线

从仿真结果中可以看出，对于卫星移动终端分布式天线系统，未经过时延调整补偿的时延对齐简化方案信号间的时延差呈现锯齿形变化，这是因为每个估计周期内信号仅进行一次时延估计，在此周期内随着终端的移动信号间的时延差会发生变化，从而带来信号间的时延误差，此误差直到下个估计周期才得以纠正。如果按照本文提出的调整策略，根据卫星终端的移动速度、方向、角度变化等情况，在一个时延估计周期内对信号间的时延差进行动态调整，则可以使信号间的时延差保持在一个平稳的水平，从而可以直接利用估计出的时延差值作为信号对齐的依据。

4 结束语

本文主要针对分布式相控阵天线信号间的时延估计方案进行研究，建立了分布式天线的信号模型，研究了一种可用于本系统的分布式天线时延对齐方案，即基于合成信号的分布式天线时延对齐方案，详细介绍方案的原理并对终端移动过程中的时延估计方案进行了简化，引入动态调整策略对简化方案中的时延差误差进行了补偿。仿真表明，本文提出的多路时延估计方案能够在时延估计性能上得到一定的提升，同时简化方案中的动态调整策略也能够将误差控制在较小的范围之内。

[1] Shen C,Yu H. Time-delayAlignment Technique for a Randomly Distributed Sensor Array[J]. Communications Iet,2011,5(8):1068-1072.

[2] Benesty J,Huang Y,Chen J. Time Delay Estimation via Minimum Entropy[J]. IEEE Signal Processing Letters,2007,14(3):157-160.

[3] Chen J,Benesty J,Huang Y. Robust Time Delay Estimation Exploiting Redundancy Among Multiple Microphones[J]. Speech & Audio Processing IEEE Transactions on,2003,11(6):549-557.

[4] Ianniello J P. High-resolution Multipath Time Delay Estimation for Broad-band Random Signals[J]. IEEE Transactions on Acoustics Speech & Signal Processing,1988,36(3):320-327.

[5] Reed F,Feintuch P L,Bershad N J. Time Delay Estimation Using the LMS Adaptive Filter-Static Behavior[J]. IEEE Transactions on Acoustics Speech & Signal Processing,1981,29(3):561-571.

[6] So H C,Ching P C. Comparative Performance of LMSTDE and ETDE for Delay and Doppler Estimation[C]∥ Signals,Systems and Computers,1994. 1994 Conference Record of the Twenty-Eighth Asilomar Conference on. IEEE,1994:1501-1505.

[7] Benesty J,Chen J,Huang Y. Time-delay Estimation via Linear Interpolation and Cross Correlation[J]. Speech & Audio Processing IEEE Transactions on,2004,12(5):509-519.

[8] Chen J,Huang Y,Benesty J. Time Delay Estimation Via Multichannel Cross-Correlation:Audio Signal Processing Applications [C]∥ IEEE International Conference on Acoustics,Speech and Signal Processing. IEEE,2005:49-52.

[9] Huang Y,Benesty J,Chen J. Laplace Entropy and Its Application to Time Delay Estimation for Speech Signals[C]∥ IEEE International Conference on Acoustics,Speech and Signal Processing. IEEE,2007:113-116.

[10]Griebel S M,Brandstein M S. Microphone Array Source Localization Using Realizable Delay Vectors[C]∥ Applications of Signal Processing to Audio and Acoustics,2001 IEEE Workshop on the. IEEE,2001:71-74.

[11]So H C,Ching P C. Comparative Study of Five LMS-based Adaptive Time Delay Estimators[J]. Radar,Sonar and Navigation,IEE Proceedings,2001,148(1):9-15.

[12]Cheng Z,Tjhung T T. A New Time Delay Estimator Based on ETDE[J]. IEEE Transactions on Signal Processing,2003,51(7):1859-1869.

Delay Estimation Scheme of Distributed Phased Array Antenna for Satellite Terminal

MA Chun-yang,LI Jian,LUO Yong,CHENG Yu-xin,WU Jian-jun

(Modern Communications Research Institute,School of Electronics Engineering and Computer Science, Peking University,Beijing 100871,China)

Aiming at the problems of the traditional estimation scheme of time delay in distributed phased array antenna system of satellite terminal,this paper studies the multi-channel delay estimation scheme based on the synthesized signal,and designs the dynamic adjustment strategy of the simplified scheme. The results of simulation show that this scheme can effectively improve the performance of delay estimation,reduce the complexity of algorithm. The simplified scheme of delay estimation of adding dynamic strategy can reduce the error of system.

distributed phased array antenna; delay estimation; composite signal; dynamic adjustment

2017-06-09

国家自然科学基金项目(61371073)

马春阳(1992—)，女，硕士研究生，主要研究方向：卫星通信。吴建军(1968—)，男，教授，博士生导师，主要研究方向：宽带卫星通信系统和技术、同轴宽带有线接入技术、3G/4G移动通信及网络技术、超宽带通信技术、嵌入式系统软硬件技术。

10.3969/j.issn.1003-3114.2017.05.15

马春阳,李健,罗勇,等. 卫星终端分布式相控阵天线时延估计方案[J].无线电通信技术,2017,43(5): 67-70，83.

[MA Chunyang,LI Jian,LUO Yong,et al. Delay Estimation Scheme of Distributed Phased Array Antenna for Satellite Terminal [J]. Radio Communications Technology,2017,43(5):67-70，83.]

TN821+.8

A

1003-3114(2017)05-67-4