圆柱指数型复合型变幅杆的动力学分析

刘 垚，李 斌

（1.山西大学动力工程系，山西太原030006；2.山西省特种设备监督检验研究院，山西太原030006）

圆柱指数型复合型变幅杆的动力学分析

刘 垚1，李 斌2

（1.山西大学动力工程系，山西太原030006；2.山西省特种设备监督检验研究院，山西太原030006）

超声波加工中的变幅杆能放大振幅，并将声能有效传递至工具头。为使变幅杆工作有效、可靠，进而提高零件加工的精度和效率，变幅杆必须具有良好的动态特性。由于复合型变幅杆的截面复杂，用解析法无法进行求解计算，而有限元方法能较好地解决该问题。通过模态分析并利用ANSYS有限元软件，对复合型变幅杆进行动力学分析，最终找出了最佳振动形态的工作频率。

超声波加工；变幅杆；有限元；动态特性

变幅杆有时候也称作超声变速杆，它是把超声波能量聚在一起的工具。在超声加工中，变幅杆的作用是把质点振动位移和振动速度放大，同时与换能器进行阻抗匹配，与之产生共振效果。由此就能把超声波发生器的声能有效地传递到工具头上，产生高频振动作用[1-2]。

考虑到圆柱指数型复合型变幅杆的截面是从单一的圆柱面到复杂的指数型截面变化，波动方程无法进行精确求解，而利用有限元方法能准确计算出结果。有限元的原理是建立在变分计算的基础上，利用计算机进行数值计算，可解决工程上的许多问题[3-4]，如在弹塑性力学和动力学上的求解计算等。因此，本文使用有限元方法精确求解出圆柱指数型复合型变幅杆的性能参数。

1 模态分析

模态分析的基本思路是将研究对象划分为有限个单元，单元节点e的位移列向量以{x(t)}e表示，利用位移插值方式，单元e中任意一点的位移{f(t)}可用如下矩阵方程来表示[5-6]：

式中：[N]为形状函数矩阵。

在单元e中任意一点的应变向量为：

式中：[B]为几何矩阵。

在单元e中任意一点的应力为：

式中：[D]为弹性矩阵。

在单元e中任意一点的刚度矩阵为：

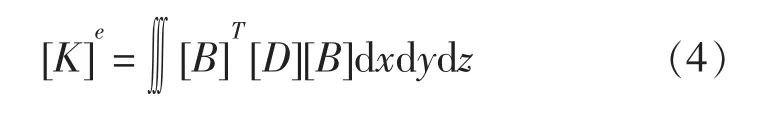
解决弹性体自由振动问题常用的动力基本方程为：

式中：[M]为质量矩阵；[K]为刚度矩阵。

由于一系列简谐振动的叠加组成了弹性体的自由振动，所以求解弹性体自由振动的固有频率和相应振型，需用到简谐运动方程：

式中：{g}为振幅列向量；{x(t)}为位移；ω为固有频率。

将式（6）代入式（5），并消去sinωt因子，可得到：

式中：ω2为广义特征值；{g}为广义特征向量。

求解式 （7）所得到的ω就是弹性体的固有频率，{g}就是相应的振型。

2 有限元分析

2.1 对变幅杆进行类型选择，建立实体模型并划分网格

选取SOLID185固体模型，定义材料的弹性模量为200 GPa、泊松比为0.3、密度为7800 kg/m3。通过ANSYS有限元分析软件建立变幅杆的实体模型，然后进行网格划分，建立的有限元模型见图1。

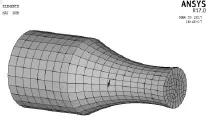
图1 变幅杆的有限元划分

2.2 对变幅杆施加载荷并求解

在有限元软件分析过程中，需指定分析类型为模态分析，求解计算的方法为子空间迭代法，求解的频率范围选定为19～21 kHz，所得结果数目取个数为5。

在求解分析过程中，对变幅杆的输入端施加一个0.01 mm的位移约束，输出端设置为自由端，求解出的结果写入一个固定的文件中。

2.3 对变幅杆进行计算及分析

利用软件后处理器将模态计算结果记录在结构分析文件中，记录的数据结构包含变幅杆的频率、振型和应力，对于这些结果的准确度则取决于上述变幅杆单元网格的划分。在五个不同的固有频率下，变幅杆产生的纵向振动见图2。可见，在不同频率下的振动变形是不同的，在频率为19.599 kHz时变形最小，且振动形态最佳。因此，超声波发生器的工作频率选为19.599 kHz，变幅杆在该频率下可达到最大振幅。

图2 变幅杆在不同频率下的纵向振动

3 结束语

本文利用ANSYS有限元分析软件求解分析圆柱指数型复合型变幅杆，通过建立变幅杆的实体模型及有限元分析，找出超声波信号传导至变幅杆的共振频率数值，得出变幅杆的动力分析结果，并求解出最佳振动形态。

[1] 林书玉，张福成.大尺寸矩形断面超声变幅杆固有频率的研究[J].声学学报，1992，17（6）：451-455.

[2] 俞宏沛.非轴对称变幅杆的设计及阶梯形变幅杆圆滑过渡的研究[J].声学与电子工程，1994（1）：9-13.

[3] LEE M，YOO Y H.Analysis of ceramic/metal armour system[J].International Journal of Impact Engineering，2001，25（9）：819-829.

[4] PEI Z J，FERREIRA P M.Modeling of ductile-mode materialremovalin rotary ultrasonic machining[J]. International Journal of Machine Tools&Manufacture，1998，38：215-220.

[5] 朱伯芳.有限单元法原理与应用[M].北京：水利电力出版社，2006.

[6] LEE T C，CHAN C W.Mechanism of the ultrasonic machining of ceramic composites[J].Journal of Materials Processing Technology，1997，7（1）：195-201.

欢迎订阅《电加工与模具》

《电加工与模具》是我国特种加工和模具制造领域国内外公开发行的专业性技术刊物，由苏州电加工机床研究所和中国机械工程学会特种加工分会主办。

主要报道内容为：特种加工（包括电火花加工、电化学加工、激光加工、增材制造/3D打印、超声加工等）和模具制造领域的设计研究成果、工艺应用技术、使用维修经验、产品开发信息和行业发展动态等。

本刊为双月刊，邮发代号：28-36，全国各地邮局均可订阅。每期定价10元，全年60元。

编辑部地址：江苏省苏州高新区金山路180号。电话：0512-67274541。

Dynamic Analysis of the Cylinder-index Amplitude Transformer

LIU Yao1，LI Bin2
（1.Department of Power Engineering，Shanxi University，Taiyuan 030006，China；2.Shanxi Special Equipment Supervision Inspection Institute，Taiyuan 030006，China）

The amplitude transformer of the ultrasonic machining can enlarge the amplitude and transfer the acoustic energy to the load efficiently.In order to make amplitude transformer work effective and reliable，it is necessary to have the dynamic characteristics for amplitude transformer. Because the section change of the composite amplitude transformer is complex，it is difficult to solve it by the traditional design method.The problem is usually solved by the finite element.The paper analyzes the cylinder-index amplitude transformer in dynamic performance by modal analysis and ANSYS computer program.Finally，the work frequency of the best form of vibration is gained.

ultrasonic machining；amplitude transformer；finite element；dynamic performance

TG663

A

1009－279X（2017）03－0061-02

2017-04-07

精密加工山西省重点实验室开放课题（20160121）

刘垚，男，1981年生，副教授。