基于三角波瓣混合器的超声速流场精细结构和掺混特性∗
2017-08-09张冬冬谭建国李浩侯聚微
张冬冬 谭建国 李浩 侯聚微
(国防科学技术大学,高超声速冲压发动机技术重点实验室,长沙 410073)
基于三角波瓣混合器的超声速流场精细结构和掺混特性∗
张冬冬†谭建国 李浩 侯聚微
(国防科学技术大学,高超声速冲压发动机技术重点实验室,长沙 410073)
(2016年12月24日收到;2017年3月6日收到修改稿)
在超声速吸气式混合层风洞中,采用基于纳米粒子的平面激光散射(NPLS)技术对平板混合层和三角波瓣混合器诱导的混合层流场精细结构进行了对比实验研究.上下两层来流的实测马赫数分别为1.98和2.84,对流马赫数为0.2.NPLS图像清晰地展示了Kelvin-Helmholtz涡、流向涡、波系结构以及大尺度涡结构的配对合并过程.通过对比分析时间相关的NPLS流场图像,发现了大尺度拟序结构随时间发展演化的非定常特性.基于流动显示结果,采用分形维数和间歇因子指标对流场结构和混合特性进行了定量分析.实验研究表明,三角波瓣混合器诱导的流向涡结构显著提高了上下两层来流的掺混效率,其流动远场的分形维数突破了平板混合层中完全湍流区的分形维数值,达到了1.88,流场结构表现出明显的破碎性,有利于流动在标量层面的扩散和掺混.流动间歇性分析表明,流向涡与展向涡的相互剪切作用主导着混合层的掺混特性,同时由于流向涡的卷吸作用,三角波瓣混合器诱导的混合层混合区域更大,更多的流质被卷入混合区完成混合.
∶超声速混合层,波瓣混合器,分形,间歇性
PACS∶47.40.Ki,47.80.Jk,47.40.—x,47.15.StDOI∶10.7498/aps.66.104702
1 引 言
近年来随着超燃冲压发动机(scramjet)技术的发展,高速可压缩条件下空气与燃料的快速掺混成为国内外竞相研究的热点[1,2].超燃冲压发动机燃烧室尺寸有限,时间尺度为毫秒量级,如何在较短的时间内实现超声速空气与燃料的快速掺混成为超燃冲压发动机最为核心的一项关键技术[3].为更深入地研究超燃冲压发动机中空气与燃料的混合机理,迫切需要开展超声速湍流混合层的研究.此外,一般认为混合层的失稳源于Kelvin-Helmholtz(K-H)涡的对并以及涡结构之间的相互作用,研究超声速条件下混合层的增长特性有助于明确混合层失稳导致混合增强的理论机制.同时,作为自由剪切层的一种重要形式,混合层结构简单,不受壁面干扰,深入研究其流场中大尺度拟序结构的运动和小尺度涡结构的脉动特性,有助于加深对湍流这一长久以来困扰研究人员的经典问题的理解[4].
自Brown和Roshko[5]首次通过实验观测到混合层中规则的大尺度涡结构后,研究人员在湍流的研究中达成一种共识∶混合层并不是一种完全无序的结构,其在发展过程中具有统计的特性,大尺度拟序涡结构的配对和合并主导着流动的发展[6,7].对于低速不可压混合层流动而言,受K-H不稳定性影响卷起的展向涡结构的尺度快速增长,能够有效促进上下两层来流的掺混[5].而在超声速流动状态下,受到可压缩效应的影响,展向涡的发展和演化受到显著的抑制,导致其在混合层增长过程中的作用大大减弱[8].Freund等[9]通过实验研究表明,在上下两层来流的密度比相同的条件下,可压缩混合层的增长率只有不可压条件下的20%.考虑到超声速条件下较低的混合效率,有必要采取一系列混合增强措施来促进流动的掺混.Martens等[10]通过在超声速混合层入口引入电火花激励,研究了对流马赫数(Mc)分别为0.5和0.64情况下超声速混合层的增长特性,两种对流马赫数下混合层的增长率从0.032分别增长到0.079和0.137.Doty和Mclaughlin[11]采用纹影技术获得了振动薄平板控制下混合层的增长特性,其研究发现控制振动频率为20 kHz时,混合层的增长率提高了50%,获得了最优的掺混效果.
此外,由于流向结构的产生和演化特性受可压缩效应影响较小,向流场中引入流向涡来促进流动的混合得到了持续不断的研究[12,13].这其中波瓣结构作为诱导流向涡结构最为有效的装置,在超声速混合增强中受到了广泛的关注和应用[14,15].Paterson[16]首先通过实验研究了波瓣混合器促进流动混合,其研究结果认为波瓣下游的横向对流作用导致了流向涡的产生,并且流向涡在演化过程中通过增大流动的接触面积促进上下来流的掺混.Tew等[15]系统研究了压缩性对基于波瓣混合器的超声速混合层流场的特性,认为高可压缩性严重抑制了展向涡的增长,这给流向涡提供了更多的时间和空间来拉伸和扭曲标量接触面积,从而促进掺混.波瓣混合器诱导的大尺度涡结构的卷吸作用被认为是流向涡促进掺混的重要因素,但是波瓣结构作用下流场结构的三维演化特性以及流向涡与K-H涡的相互作用对混合过程的影响尚未明晰,波瓣混合器促进混合增强的机理尚未形成定论.此外由于实验条件的限制,三角波瓣结构诱导的具有高时空分辨率、高信噪比的流场精细结构也鲜见报道.
基于此,本次研究采用基于纳米粒子的平面激光散射(nanoparticle-based planar laser scattering,NPLS)技术对平板混合层和三角波瓣混合器诱导下的混合层流场结构进行了对比实验研究,获得了流场的精细结构,比较了这两种流动在流场结构发展演化、流动混合等方面的特点.采用分形维数和间歇因子指标,定量分析和讨论了三角波瓣结构对于促进流动掺混的作用,提出了流向涡促进掺混的机理.
2 实验装置
2.1 超声速混合层风洞
本次实验采用的是低噪声,低湍流度的超声速吸气式混合层风洞,如图1所示.风洞由过渡段,整流段,喷管段,实验段以及扩压段五部分组成,后面与真空罐相连.通过分隔板将风洞分为上下两层,双马赫数喷管的型面均采用基于B样条曲线的轴线配置马赫数的特征线方法设计,能够提供均匀稳定的超声速来流.整流段上游的压力调节器用于调节上层低马赫数来流的总压,从而在喷管出口处实现上下两层来流的静压匹配.

图1 超声速混合层风洞Fig.1.Supersonic mixing layer wind tunnel.
2.2 实验参数校测
实验设计的喷管马赫数为2.0和3.0,实际上由于加工精度,安装调试中不可避免地存在一定的误差,有必要采用正激波关系式对流场的实际马赫数进行校测.正激波前后的总压满足下式∶

式中,γ为比热比,对于空气γ=1.4;M为喷管出口的实际马赫数;P01和P02分别为正激波前后的总压.对于超声速混合层而言,正激波的波后总压采用流场中置入的总压耙测得,将测压孔水平置于来流中,使测压孔前方产生正激波,总压耙测得的压力即为波后总压.由于整流段内部的气体速度较低,可认为喷管入口处的压力为正激波前的总压,因此喷管入口处的压力可由喷管前缘的壁面静压孔测得.图2为流场校测时采用高频压力传感器采集的上下两层来流的压力信号分布.风洞运行时,上下两层来流的激波前后总压分别稳定在26.4 kPa和19.2 kPa,99.1 kPa和37.3 kPa,由此通过迭代法得到上下来流的实际马赫数分别为1.98和2.84.
喷管出口的静压和静温可以通过等熵关系式和声速关系式给出∶
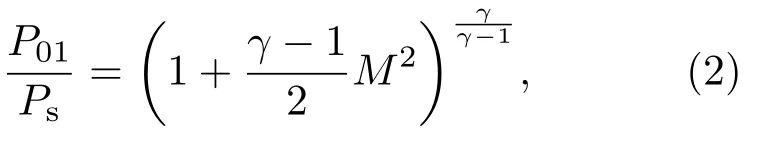

图2 (网刊彩色)压力信号分布Fig.2.(color online)Distribution of pressure signal.
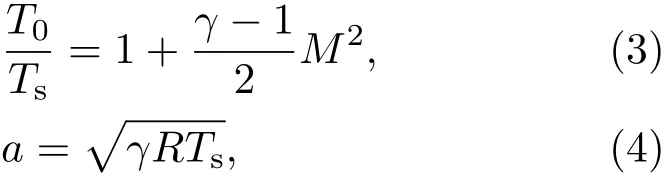
式中,Ps和Ts分别为喷管出口的静压和静温;T0为来流总温,其值为实测的大气温度300 K;a为当地声速;R为气体常数,取R=287 J·kg−1K−1.采用声速关系式,求得上下两层来流的当地声速,进而求得混合层的对流马赫数.风洞流场的校测值如表1所列.

表1 风洞流场校测参数Table 1.Calibrated parameters of wind tunnel.
2.3 NPLS系统
本次实验研究采用NPLS技术[17,18]获得了具有高时空分辨率的流场精细结构图像.NPLS系统由脉冲激光器、纳米粒子发生器、同步控制器、CCD相机以及计算机组成,如图3所示.其中,同步控制器用来控制系统各个部件协同工作,其时间精度达到了250 ps,跨帧CCD相机的分辨率为4008×2672,其双曝光的最短时间是0.2µs,激光光源采用波长为532 nm,脉冲时间为6 ns的双腔Nd∶YAG激光器,其单脉冲激光能量最高为500 mJ.实验时,通过纳米粒子发生器向流场中均匀撒播名义粒径为50 nm的TiO2作为示踪粒子,可以有效散射激光以获得高信噪比的实验图像.NPLS系统已经成功应用于超声速湍流复杂流场的精细测量,能够清晰地获得激波、膨胀波、马赫盘、混合层、边界层等超声速典型流场精细结构[17−19].

图3 NPLS系统示意图[17]Fig.3.Schematic of NPLS system[17].
2.4 实验模型
为深入研究流向涡诱导混合增强的机理,设计了平板混合层和三角波瓣构型混合层实验件,两种工况的中间隔板厚度均为1 mm,如图4(a)和图4(b)所示.三角波瓣涡流发生器安装于隔板的尾缘,如图4(c)所示.三角波瓣构型的设计主要存在两个参数∶波瓣的倾斜角α和波瓣的波瓣波长λ.倾斜角越大,则产生的流向涡强度越大,但同时也会造成流动在隔板后缘的分离,增加流动阻力不利于混合.Tew[20]研究指出当波瓣倾斜角大于15◦时流动将发生分离.基于此,综合考虑流向涡强度和流动分离情况,设计选取了波瓣的倾斜角为10◦.波瓣波长选取为11.8 mm,这一值与文献[7]中研究得出的展向涡结构的典型波长相同.此外波峰和波槽之间通过1/4个波瓣波长的等直段连接,这样设计的好处是减少波峰和波槽区域产生的流向涡的相互干扰,方便单独研究每个流向涡对流场掺混的影响[21].对于三角波瓣混合器混合层,采用跨帧CCD相机分别拍摄了Y=0和Y=1/4λ位置处的流场结构;对于平板混合层在平板后缘的中间位置处进行了拍摄.
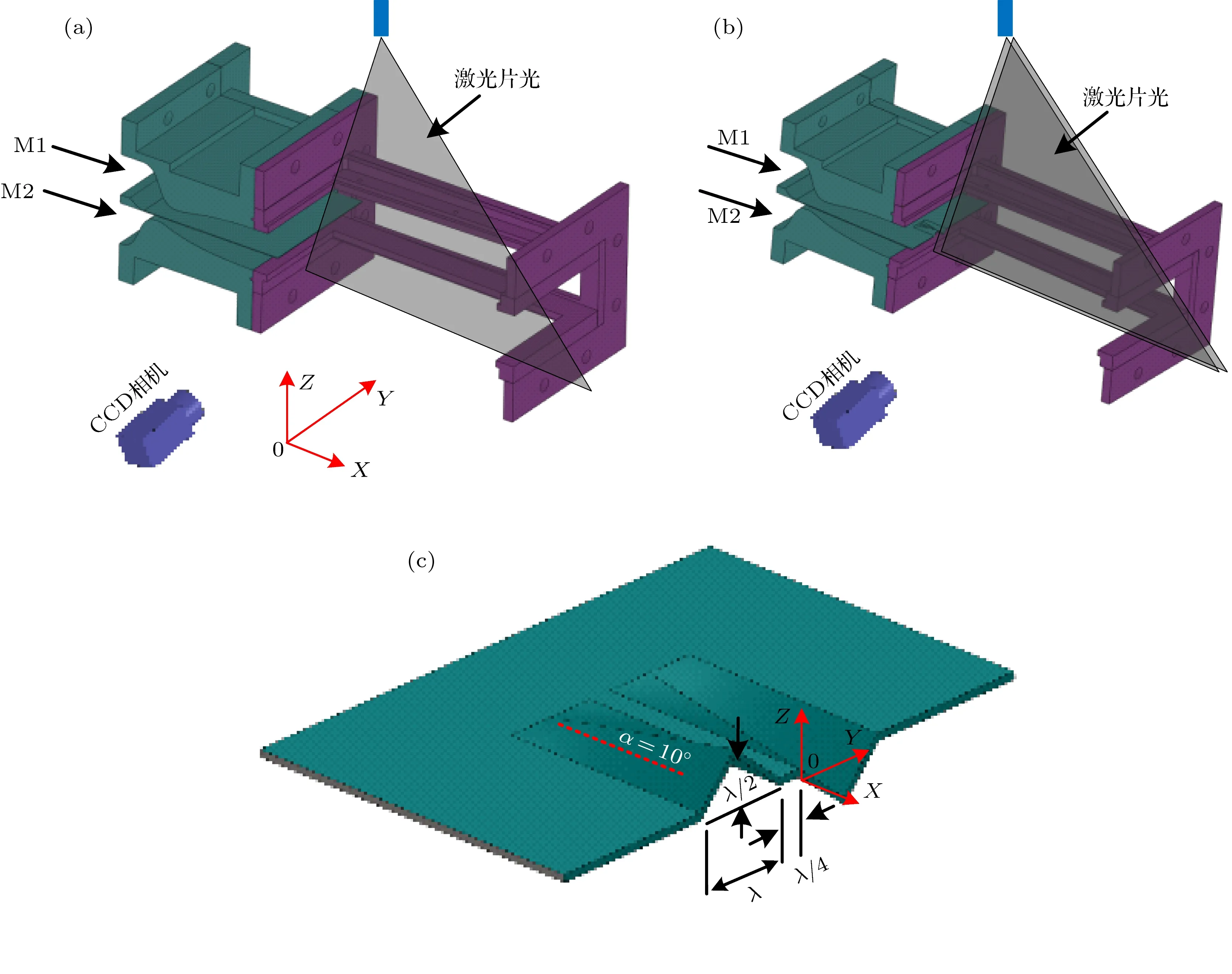
图4 (网刊彩色)实验件模型 (a)平板混合层;(b)三角波瓣混合器混合层;(c)三角波瓣构型Fig.4.(color online)Test model:(a)Planar mixing layer;(b)mixing layer with triangular lobed mixer;(c)configuration of triangular lobes.
3 实验结果与分析
3.1 流场结构显示
图5(a)为平板混合层流场下游的精细结构图像,图像的空间分辨率为50.6µm/pixel.在初始K-H不稳定性作用下,混合层在经过一小段波动后迅速卷起形成K-H涡结构,并且涡结构卷起的方向为逆时针向来流方向倾斜,这是由于下层来流速度大于上层来流速度所致.K-H涡结构在向下游发展演化过程中出现多次的配对与合并现象,这与Brown和Roshko[5]在低速不可压流动中观测到的K-H涡的对并现象相同,证实了这种大尺度拟序涡结构在超声速混合过程中依然存在.在流向X=60 mm处,流动进入转捩区,K-H涡结构开始破碎.在X=80 mm处破碎过程完成,之后流动进入了完全湍流区,流动在这个阶段受小尺度涡结构的脉动控制.在平板混合层涡卷起阶段,一系列小激波结构从大尺度K-H涡结构的涡源处产生,并且在远场处偏转,形成类似于弓形激波的结构.Dimotakis[22]和Rossmann等[23]均指出小激波结构一般出现在高对流马赫数的混合层流动中,其原理在于K-H涡前的超声速气流被涡面压缩从而形成激波结构.而本次研究证实了低对流马赫数流动中也可能出现小激波结构,其产生的机理在于来流在平板后缘相遇后速度的强烈剪切作用导致K-H涡的迅速卷起,混合层受到K-H涡面的强烈压缩作用使得在低对流马赫数中出现了小激波结构.值得注意的是,这种小激波结构的出现对于流动的混合是无益的,其原因在于涡结构之间出现的小激波使得两股来流的相互对流过程不再是等熵过程,波后的总压减小,从而导致流动的总能量损失.图5(b)为Olsen和Dutton[24]研究的对流马赫数为0.38的混合层流场图像,可以发现相比于本次研究对流马赫数为0.2的流动,对流马赫数的提高导致了混合层的增长率受到了显著的抑制.
此外,图5(a)中上下两幅图的互相关时间为5µs,涡结构A和B在5µs时间间隔内分别向下游运动了2.79 mm和2.62 mm,然而其自身形状变化并不明显,证实了超声速混合层快运动慢变化的特点.计算可得涡结构A和B的速度分别为558 m/s和524 m/s.超声速混合层初始位置处的对流速度的计算公式为[23]
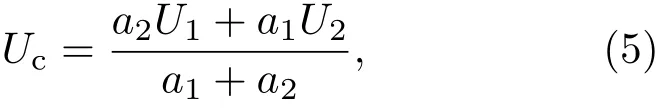
其中,a1和a2分别为高速和低速层声速,U1和U2分别为高速和低速层的速度.由前面的讨论可知,a1=215 m/s,a2=260 m/s,U1=610 m/s,U2=514 m/s.计算可得初始混合层位置处理论对流速度Uc=567 m/s,与实验值558 m/s相对误差在2%之内,基本相符.同时位于流动远场位置处的涡结构B的运动速度有所变慢,这一方面是由于远场处流动的三维特性明显,涡结构的横向运动加剧;另一方面是由于流场中存在各种波系结构导致流动的能量有所损失.

图5 平板混合层流场结构图像 (a)NPLS图像(Mc=0.2);(b)Olsen等[24]实验图像(Mc=0.38)Fig.5.Images of planar mixing layer flow structures:(a)NPLS images(Mc=0.2);(b)experimental images obtained by Olsen et al.[24](Mc=0.38).
图6为三角波瓣混合器诱导下的混合层流场结构的精细图像,(a)和(b)分别在Y =1/4λ和Y =0位置处拍摄,图像的空间分辨率为50.6µm/pixel.相比于平板混合层,流动在经过混合器后面的一小段层流区域后并没有卷起成大尺度的K-H涡结构,而是破碎成明显的小尺度涡,小尺度涡结构有助于增加流动的接触面积,从而加速流动在接触面上标量的混合.此外在Y=0处,流向涡与展向涡结构的相互作用非常剧烈,流场表现出明显的三维特性.经过混合器的混合层结构被分为三个部分I,II和III.I对应于波峰位置诱导的流向涡,II位置对应于中间平板处诱导的流向涡结构,这两个流向涡结构在向下游发展过程中均形成了涡簇结构带.Vaghef i等[25]研究指出,湍流混合中上下两层流动的卷吸过程可通过下面两种机理产生∶小尺度涡结构的撕咬(nibbling)和大尺度涡结构的吞噬(engulfment).在三角波瓣混合器流场中,涡簇结构带(I和II)破碎形成的小尺度涡结构之间的相互撕咬作用有效地扩大了标量混合接触的表面积,加速了上下两层流动的质量,动量和能量的交换;同时相比于平板混合层,流场中卷起的展向涡的尺度更大(III),并且在下游远场处仍然保持着大尺度结构的完整性,大尺度涡结构卷吸和吞噬着周围的流体进入混合区域,有效增强了流动的混合.

图6 三角波瓣混合器流场图像Fig.6.Flow structures of triangular lobed mixer.
3.2 分形分析
在超声速混合层流动中,由于存在激波,剪切层和流向涡等复杂的流场结构,使得采用传统的几何度量方法无法对流动的分界面曲线进行定量化的分析.由于超声速混合层不具有特征长度,且其具有整体和局部的自相似特性,非常适合采用分形维数来描述其分界面的特征.Sreenivasan[26]首先将分形理论引入到湍流的测量与研究中,其定义一条直线、一个平面的分形维数分别为1和2,从而任意一个二维的复杂曲线的分形维数都介于1和2之间,并且分形维数越高,曲线的破碎性越强,对应于混合层中则是小尺度涡结构的脉动越剧烈,流场的三维特性越明显.
分形维数的计算方法有很多,包括频域方法,计盒维数法和香肠法等.对于湍流分形的研究,Sreenivasan发现采用计盒维数法能够取得更好的效果.计盒维数法采用下式计算[27]∶

其基本原理是∶构造边长为d的正方形盒子来覆盖所要研究的平面集,计算d取不同值时盒子与平面集的相交个数Nd(F)而计盒维数就是d趋向于0时Nd(F)增加的速度.
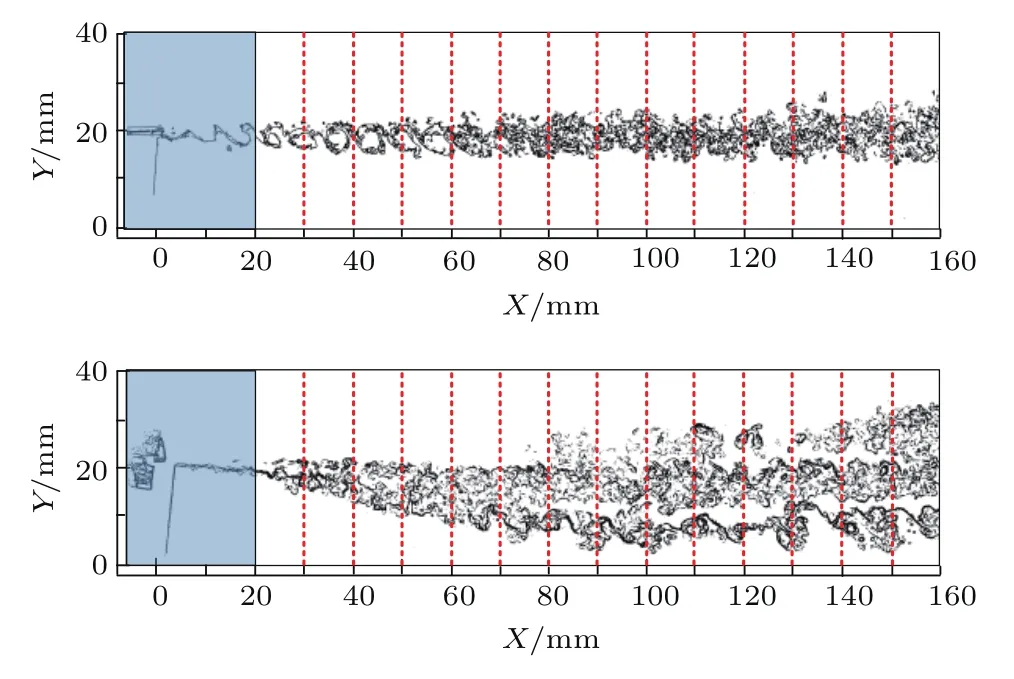
图7 流场结构边缘检测及分区Fig.7.Edge detection and partition of flow structures.
图7为采用Candy边缘检测算子[28]获得的混合层分界面曲线.为了研究流向涡结构对流场特性的影响,从流向涡出现的位置(X=20 mm)处开始计算分形维数.将流场沿流向划分为14个区域,每段区域的长度为10 mm,分别计算每段区域的分形值.图8给出了平板混合层和流向涡混合层的分形维数计算结果.在混合层的初始阶段平板混合层的分形维数有个迅速增大的过程,这是由于在这一阶段流场中展向涡结构的配对与合并过程导致涡结构与主流的分界面变得复杂和不规则.随着流动向下游的发展,大尺度涡结构开始破碎,混合层逐渐发展为湍流.大尺度结构破碎过程完成后,流动进入完全湍流区,在此区域内混合层的三维特性趋于稳定,流动的分形维数保持在1.55—1.6.对于平板混合层而言,Zhao等[28]研究指出,虽然小尺度涡结构脉动的形态各异,但完全发展湍流的分维维数基本是固定的,稳定在1.5—1.6之间,与本次研究的结论相符.流向涡流场的分形维数分布与平板混合层有着显著的不同.流向涡的出现导致流场中持续存在两种剪切作用∶上下来流的速度剪切和流向涡与展向涡的相互剪切,涡结构在向下游发展过程中破碎性逐步增加,流场的分形维数呈现出线性增长的趋势,在下游145 mm处其分形维数值达到1.88,突破了平板混合层中完全湍流区的分形维数值.这表明在流向涡流场中,相比于来流的速度剪切,流向涡与展向涡的剪切作用主导了流场中涡结构的破碎和流动三维特性的演化.

图8 分形维数分布Fig.8.Distribution of fractal dimension.
3.3 间歇特性分析
对湍流混合层而言,由于大尺度涡结构的演化和小尺度涡结构的脉动,使得混合层与主流区域的分界面是不规则且非定常的,对于分界面上的一点N而言,某一时刻处于混合层区域,而下一时刻又可能处于主流区域.湍流混合层的这种间歇特性可以通过引入间歇因子来度量.Humble等[29]通过研究将完全湍流区的间歇因子定义为1,而主流区域的间歇因子定义为0,则间歇因子γ可以定义为
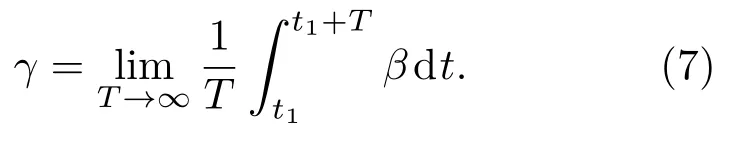
对于流场中的一点N,当其处于混合层中时β为1,处于主流区域时β为0.由此从混合层内部区域过渡到流动的主流区域,间歇因子γ从1过渡到0.
图9给出了本次研究采用的基于边缘检测计算间歇因子的方法.采用Candy边缘检测算子[28]获得流动分界面的曲线之后,在流向某一位置处自上而下进行检测,遇到第一个边缘点m时认为该点为混合层和主流的边界.对于流向涡混合层而言,流场中存在三个混合层区域(I,II和III),对于每一个混合层区域分别检测主流与混合层的边界,如图9(b)所示. 则位于m和m′,n和n′,p和p′之间的区域则为完全湍流区.

图9 边缘检测计算间歇因子方法Fig.9.Calculation method of intermittent factor using edge detection.
图10给出了平板混合层和流向涡混合层在流向位置X=80,100,120以及140 mm处的间歇因子分布曲线,每个位置处的间歇因子曲线都是基于100幅图像的计算结果.从图中可以看出,无论是平板混合层还是流向涡混合层,随着流动向下游的发展,混合层的γ分布越广,这与前面的流动显示结果相一致.同时,在同一流向位置处,流向涡混合层的γ分布范围明显大于平板混合层的γ分布,表明流向涡诱导的混合层有着更大的混合区域,更多的流质被卷入混合区域完成混合的过程.此外在流向涡的边界处γ分布更为饱满,这表明流向涡与主流边界处的涡结构具有更为强烈的脉动特性,流向涡和主流之间的质量,动量和能量交换更为剧烈.
Christensen[30]在研究湍流的统计特性时提出,当间歇因子大于0.8时,可认为流动处于完全湍流区域.基于此,本研究提出了如下混合层厚度的定义∶即对于混合层流动,基于统计特性研究的间歇因子大于0.8时对应的横向区域为混合层厚度.图11给出了四个流向不同位置处的混合层厚度分布.可以发现,对于平板混合层,在流动发展为以小尺度涡结构为主的完全湍流区域后,混合层的厚度基本保持不变;然而,随着流向涡向下游发展过程中涡簇结构带尺度的增大,流向涡诱导的混合层厚度有个显著增大的过程,这种混合层尺度的增大有利于为促进掺混提供空间,使更多的流质被卷吸进入混合区完成混合.

图10 (网刊彩色)间歇因子分布Fig.10.(color online)Distribution of intermittent factor.

图11 混合层厚度分布Fig.11.Distribution of mixing layer thickness.
4 结 论
本文在超声速吸气式混合层风洞中,采用NPLS技术对平板混合层和三角波瓣混合器诱导的混合层进行了流动显示的对比实验研究,获得了高时空分辨率的精细流动图像,清晰地捕捉到低对流马赫数中出现的小激波结构.通过分析5µs跨帧时间内的NPLS流场图像,研究了超声速流场中大尺度拟序结构随时间发展和演化的非定常特性.通过和Olsen和Dutton[24]研究的对流马赫数为0.38的混合层流场结构对比,证实了对流马赫数的提高会显著抑制混合层的增长.基于流动显示结果,采用分形维数和间歇因子指标对流场结构和混合特性进行了定量分析.
实验研究表明,三角波瓣混合器诱导的流向涡结构有效促进了上下两层来流的掺混.流向涡在向下游发展过程中形成的涡簇带结构的相互撕咬作用有效地增加了标量混合接触的表面积,同时相比于平板混合层,流向涡流场中卷起了更大尺度的展向涡结构,并且在下游远场处仍然保持着结构的完整性,这种大尺度涡结构卷吸和吞噬着周围的流体进入混合区域,有效增强了流动的混合.分形分析表明,本次实验研究工况下平板混合层中完全湍流区的分形维数值稳定在1.55—1.6之间,和Zhao等[28]的研究结论相符.而流向涡流场的分形维数呈现出线性增长的趋势,在下游145 mm处其分形维数值达到1.88,突破了平板混合层中完全湍流区分形维数值.在流向涡流场中,相比于来流的速度剪切,流向涡与展向涡的剪切作用主导了流场中涡结构的破碎和流动三维特性的演化.对间歇因子的分析表明,同一流向位置处流向涡混合层的γ分布范围明显大于平板混合层的γ分布,流向涡与主流分界面处的γ分布更为饱满,涡结构具有更为强烈的脉动特性.同时,由于流向涡的卷吸作用,三角波瓣混合器在间歇因子大于0.8时对应的横向区域更大,其诱导的混合层厚度显著增长,为流动的混合提供了更大的空间.
[1]Curran E T 2001 J.Propul.Power 17 1138
[2]Drummond J P,Diskin G S,Cutler A D 2002 AIAA Paper 2002-3878
[3]Seiner J M,Dash S M,Kenzakowski D C 2001 J.Propul.Power 17 1273
[4]Fernando E M,Menon S 1993 AIAA J.31 278
[5]Brown G L,Roshko A 1974 J.Fluid Mech.64 775
[6]Azim M A,Islam A K M S 2003 Aeronaut.J.107 241
[7]Zhang D D,Tan J G,Lü L 2015 Acta Astronaut.117 440
[8]Gutmark E T,Schadow K C,Yu K H 1995 Annu.Rev.Fluid Mech.27 375
[9]Freund J B,Lele S K,Moin P 2000 J.Fluid Mech.421 229
[10]Martens S,Kinzie K W,Mclaughlin D K 1994 AIAA Paper 1994-0822
[11]Doty M J,Mclaughlin D K 2000 AIAA J.38 1871
[12]Sunami T,Wendt M,Nishioka M 1998 AIAA Paper 1998-3271
[13]Heeb N,Gutmark E,Kailasanath K 2015 Phys.Fluids 26 086102
[14]Brinkerhof fJ R,Oria H,Yaras M I 2013 J.Propul.Power 29 1017
[15]Tew D E,Hermanson J C,Waitz I A 2004 AIAA J.42 2393
[16]Paterson R W 1982 NASA Paper CR-3492
[17]Gang D D,Yi S H,Zhao Yf2015 Acta Phys.Sin.64 054705(in Chinese)[冈敦殿,易仕和,赵云飞2015物理学报64 054705]
[18]Zhao Y X,Yi S H,Tian Lf2009 Sci.China:Ser.E 52 3640
[19]Wu Y,Yi S H,Chen Z,Zhang Q H,Gang D D 2013 Acta Phys.Sin.62 084219(in Chinese)[武宇,易仕和,陈植,张庆虎,冈敦殿2013物理学报62 084219]
[20]Tew D E 1997 Ph.D.Dissertation(Cambridge:Massachusetts Institute of Technology)
[21]Nastase I,Meslem A 2010 Exp.Fluids 48 693
[22]Dimotakis P E 1991 AIAA Paper 1991-2012
[23]Rossmann T,Mungal M G,Hanson R K 2002 J.Turbul.3 9
[24]Olsen M G,Dutton J C 2003 J.Fluid Mech.486 51
[25]Jahanbakhshi R,Vaghef iN S,Madnia C K 2015 Phys.Fluids 27 105105
[26]Sreenivasan K R 1991 Annu.Rev.Fluid Mech.23 539
[27]Humble R A,Peltier S J,Bowersox R D W 2012 Phys.Fluids 24 106103
[28]Zhao Y X,Yi S H,Tian L F,He L,Cheng Z Y 2009 Sci.China:Ser.G 51 1134
[29]Humble R A,Peltier S J,Bowersox R D W 2012 Phys.Fluids 24 106103
[30]Christensen E M 1973 Annu.Rev.Fluid Mech.5 101
PACS∶47.40.Ki,47.80.Jk,47.40.—x,47.15.StDOI∶10.7498/aps.66.104702
*Project supported by the National Natural Science Foundation of China(Grant Nos.11272351,91441121)and Hunan Provincial Innovation Foundation for Postgraduate,China(Grant No.CX2016B001).
†Corresponding author.E-mail:zhangdd0902@163.com
Fine flow structure and mixing characteristic in supersonic flow induced by a lobed mixer∗
Zhang Dong-Dong†Tan Jian-Guo Li Hao Hou Ju-Wei
(Science and Technology on Scramjet Laboratory,National University of Defense Technology,Hunan Changsha 410073,China)
24 December 2016;revised manuscript
6 March 2017)
In a supersonic suction type of mixing layer wind tunnel,by employing nanoparticle-based planar laser scattering(NPLS)method,contrast experiments are carried out with the emphasis on thefine flow structures of planar mixing layer and the mixing layer induced by triangular lobed mixer.The normal-shock equation,isentropic equation and sound speed relationship are utilized to calculate the flow parameters.The calculated Mach numbers are 1.98 and 2.84 for upper and lower airstreams respectively with a convective Mach number of 0.2.The NPLS images clearly shows the Kelvin-Helmholtz vortices,streamwise vortices,shock waves and the pairing processes of large-scale vortex structures.The unsteady properties of development and evolution for large-scale vortices are obtained by contrasting the NPLS images at different times.Also,it has been demonstrated by the present experimental investigation that in supersonic mixing layer with low convective Mach number,the small shock waves are still existing.These small shock waves that occur have negative effects on the mixing process.It is because the convection flow process of upper and lower airstreams is non-isentropic,causing the total pressure to lose.Based on the NPLS results, flow structures and mixing characteristics are analyzed quantitatively by using fractal and intermittency theory.The results show that the mixing efficiency increases obviously with the introducing of large-scale streamwise vortices.The nibbling of vortex clusters induced by large-scale streamwise vortices obviously increases the interface area of mixing.Meanwhile,compared with planar mixing layer,larger spanwise structures rollup in triangular lobed mixing layer,leading to more entrainment of upper and lower airstreams.In the present investigation of supersonic planar mixing layer,the value of fractal dimension of fully turbulent region is stable at 1.55–1.6.Whereas the value of fractal dimension for triangular lobed mixing layer reaches 1.88 at the flow field far away downstream,which breaks through the value of fully developed turbulence for planar mixing layer.Besides,in triangular lobed mixing layer,the shear action between streamwise vortices and spanwise structures plays a leading role in promoting mixing.The mixing flow shows the property of apparent crushability and three-dimensional behavior,which plays a positive role in promoting mixing at a scalar level.The analysis of intermittency indicates that the interaction between streamwise and spanwise vortices dominates the mixing characteristics,and due to the entrainment of streamwise vortices,the mixing region induced by triangular lobed mixer becomes larger,and morefluids are engulfed into the mixing region to complete the mixing process.
∶supersonic mixing layer,lobed mixer,fractal,intermittency
∗国家自然科学基金(批准号:11272351和91441121)和湖南省研究生科研创新项目(批准号:CX2016B001)资助的课题.
†通信作者.E-mail:zhangdd0902@163.com
©2017中国物理学会Chinese Physical Society
