采用高信噪比电磁诱导透明谱测定85Rb原子5D5/2态的超精细相互作用常数∗
2017-08-09杨光王杰王军民
杨光 王杰 王军民
1)(山西大学光电研究所,太原 030006)
2)(量子光学与光量子器件国家重点实验室,山西大学,太原 030006)
3)(极端光学协同创新中心,山西大学,太原 030006)
采用高信噪比电磁诱导透明谱测定85Rb原子5D5/2态的超精细相互作用常数∗
杨光1)2)王杰1)2)王军民1)2)3)†
1)(山西大学光电研究所,太原 030006)
2)(量子光学与光量子器件国家重点实验室,山西大学,太原 030006)
3)(极端光学协同创新中心,山西大学,太原 030006)
(2017年1月16日收到;2017年3月3日收到修改稿)
基于85Rb原子5S1/2-5P3/2-5D5/2阶梯型能级系统(780 nm+776 nm),利用高信噪比的电磁诱导透明谱对85Rb原子5D5/2态超精细分裂进行测量.其中,频率校准是通过位相型电光调制器和共焦法布里-珀罗腔共同实现的.通过测量85Rb原子5D5/2态(F′′=5),(F′′=4)及(F′′=3)之间的超精细分裂,我们确定了85Rb原子5D5/2态的磁偶极超精细相互作用常数(A=−(2.222±0.019)MHz)和电四极超精细相互作用常数(B=(2.664±0.130)MHz).
∶超精细分裂,电磁诱导透明,电光调制器,法布里-珀罗腔
PACS∶32.10.Fn,42.50.Gy,42.50.HzDOI∶10.7498/aps.66.103201
1 引 言
原子核与核外电子的超精细相互作用导致超精细结构的产生,其精密测量备受关注,因为它不仅可以检验一些基本物理问题的准确性,而且可以提供精确的频率基准.超精细结构在宇称不守恒测量[1]、高分辨率光谱、激光冷却与俘获等方面有着广泛的应用.但关于超精细结构常数精密测量的数据不多,尤其是D态.由于D态原子强的关联效应,导致D态原子超精细分裂准确计算充满挑战[2],因此D态原子超精细分裂精密测量对于原子复杂内禀属性的理论计算具有重要的参考意义.近些年来,精密光谱、光频梳、冷原子等技术的发展极大地推动了超精细结构测量的发展.国内外许多研究小组先后都开展了关于碱金属原子超精细结构测量的研究,尤其是铷和铯.Nez等[3,4]采用无多普勒双光子谱的方法测量了铷原子5D态超精细相互作用常数,Grove等[5]利用光学双共振谱测量了铷原子5D5/2态超精细结构,Stalnaker等[6]利用飞秒光频梳测量了铯原子超精细结构的绝对频率,Gabbanini等[7]采用共振增强离子化谱测量冷原子中铷原子5D态超精细结构常数.
我们利用电光调制的共焦法布里-珀罗腔(confocal Fabry-Perot cavity,CFP)作频率标尺,测量了铯原子7S1/2态[8]、8S1/2态[9]及铷原子4D5/2态[10]的超精细结构常数.对于85Rb原子5D5/2态,由于其超精细分裂较小,光谱较难分辨,故实验测量结果并不多且都是之前的结果[3−5,7].原子相干效应可以很好地解决这一问题,它已经改变了我们对于一些传统的非线性过程的认识,比如参量过程、二次谐波、四波混频等[11−13],这些过程的效率可以非常高,注入功率可以非常小,达到少量光子量级[14],电磁感应透明(electromagnetically induced transparency,EIT)在其中扮演着非常重要的角色.EIT是基于原子相干对吸收的相消干涉使介质的吸收和色散特性发生变化[15].自从1989年Harris等在理论上提出EIT[11]以及1991年Boller等[16]在锶原子气室和Field等[17]在铅原子气室中实现EIT以来,就得到了人们广泛的关注.人们已将EIT推广到原子束[18]、固体[19]、冷原子[20],玻色-爱因斯坦凝聚[21],并将其应用到众多领域,如光存储[22,23]、光速控制[24]、量子信息处理[25,26],高分辨率磁强计[27]、高分辨率光谱[28]等.EIT通常是基于一个理想的三能级原子与两相干光场相互作用的结果∶较强的耦合光会导致原子能级之间的量子干涉,使得原子对较弱的探测光吸收减弱从而变得透明.三能级的原子构型可以为Λ型、V型、阶梯型[29,30].

图1 (网刊彩色)85Rb原子相关超精细能级图[3,4],能级结构之间的数字代表超精细分裂,单位为MHzFig.1.(color online)Relevant hyperfine levels of85Rb atom[3,4](not to scale).The numbers between the energy levels represent the numerical values of the hyperfine splitting inmegahertz.
与87Rb原子5S1/2-5P3/2-5D5/2阶梯型能级系统相比[29,31],85Rb系统研究的并不多,因为85Rb原子5D5/2态超精细分裂更小,比87Rb原子小一个数量级.文献[3,4]给出的85Rb原子的5S1/2,5P3/2,5D5/2态能级的超精细态及超精细分裂值如图1所示.本文拟从实验上更精确地测量85Rb原子的5D5/2态能级的超精细分裂,并确定5D5/2态能级的磁偶极超精细相互作用常数A和电四极超精细相互作用常数B.
较弱的探测光锁定在5S1/2(F =3)-5P3/2(F′=4)循环跃迁上,较强的耦合光在5P3/2-5D5/2之间进行扫描,得到的EIT光谱具有平坦的背景,因而信噪比大幅提高.由于85Rb原子5D5/2态的超精细结构非常小(小于10 MHz),为了提高光谱的分辨率,在探测光与耦合光反向传播、均为水平偏振的条件下,我们研究了其强度对阶梯型EIT线型的影响,进而获得了高信噪比的EIT光谱.EIT光谱包含超精细结构的信息,我们利用位相型电光调制器(phase-type electro-optic modulator,EOM)结合CFP的方法来提取该信息,然后测得85Rb原子5D5/2态的超精细分裂,进而计算出其磁偶极超精细相互作用常数与电四极超精细相互作用常数.
2 原 理
超精细结构是原子核与核外电子相互作用的结果.利用一阶微扰理论,我们得到超精细结构的哈密顿量为[32,33]

上式的本征能量可以写为如下的能级移动形式∶
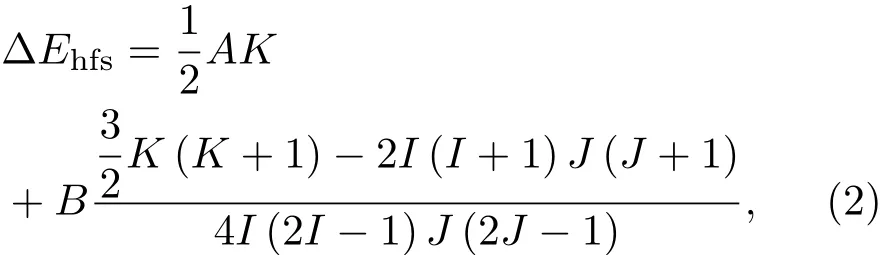
其中,K=F(F+1)−I(I+1)−J(J+1);A为磁偶极相互作用常数;B为电四极相互作用常数;I为总的核角动量;J为总的电子角动量;总的原子角动量F=I+J;I,J和F分别为I,J和F的量子数.
对于特定的态,相邻的超精细能级分裂为
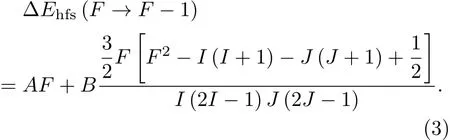
由(3)式可见,超精细相互作用常数可以由超精细分裂来确定,而超精细分裂的信息可以通过EIT谱来提取.1995年,Banacloche等[29]从半经典理论出发,对于阶梯型EIT进行了理论分析,在弱探测场近似下,可以推导出原子介质的极化率为

其中,实部χ′与原子介质的吸收系数正相关,虚部代表χ′′与原子介质的色散系数正相关.考虑到实验中探测光与耦合光反向传播且其频率接近,可以得到单位体积速度为v的原子数N(v)dv对原子介质极化率的影响为

其中,ωp与ωc分别为探测光和耦合光的频率;衰减率γij=(Γi+Γj)/2,Γi为能级|i的自发辐射衰减率;∆p为探测光相对于相应跃迁的失谐量,∆c为耦合光相对于相应跃迁的失谐量;kp为探测光的波矢,kc为耦合光的波矢;ħg21为探测光对应跃迁的电偶极矩阵元;Ωc为耦合光的Rabi频率;
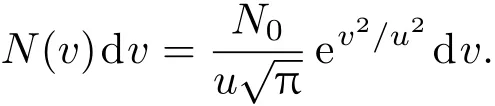
3 实验系统
图2为实验装置示意图,主要分为三个部分∶780 nm激光系统,776 nm激光系统,频率校准系统.其中,ECDL为外腔半导体激光器,OI为隔离器,λ/2为半波片,PBS为偏振分光棱镜,Triangle Wave为三角波,Rb Standard为铷原子钟,CFP为共焦法布里-珀罗腔,PZT为压电陶瓷转换器,EOM为位相型电光调制器,BD为垃圾堆,BS为分束器,µ-mental为高磁导率坡莫合金,φ为位相延迟器,Mixer为混频器,LPF为低通滤波器,PI为比例积分放大器,MTS为调制转移光谱,PD为光电探测器.

图2 (网刊彩色)实验装置示意图Fig.2.(color online)Schematic diagram of experiment setup.
780 nm激光器系统中,作为探测光(L1)的780 nm激光利用调制转移光谱(modulation transfer spectroscopy,MTS)锁定在5S1/2(F=3)-5P3/2(F′=4)循环跃迁上(循环跃迁的MTS信号强度较大,并且可以有效地减弱光抽运效应的影响),其中抽运光和探测光功率分别为164µW和26µW,调制频率为4.01 MHz(是自然线宽的0.66倍,此时MTS斜率最大).与饱和吸收谱和偏振光谱相比,MTS几乎没有背景因而有很高的信噪比,并且谱线线型受磁场、环境温度、激光偏振与光强等的影响很小,锁定后频率起伏更小[34,35].
776 nm激光系统中,耦合光(L2)与L1反向交汇于直径25 mm、长度50 mm的铷泡,夹角小于2 mrad.为了消除外界磁场的影响,铷泡被放置在由三层高磁导率坡莫合金组成的磁屏蔽筒里,剩余磁场小于0.1 mG(10 nT),这比地磁场(约为500 mG)小三个数量级.同时,磁屏蔽筒可以使铷泡同外界环境相对隔离,可以减少环境温度起伏对于铷原子热运动的影响.L1与L2的光束直径均为2.0 mm,偏振均为水平偏振.L2在5P3/2态到5D5/2态之间扫描,扫描频率120 Hz,幅度60 mV,调制端口为电流端口,我们得到85Rb原子激发态5D5/2的EIT谱.
实验中探测光和耦合光反向传播,在相同的实验条件下,同向几乎看不到EIT信号.从(5)式可以看出,同向时i(kp+kc)·v不能被忽略,此时EIT信号几乎被多普勒效应淹没.只有耦合光功率足够大时,EIT信号才出现,早期的实验证明了这一点[17].当探测光和耦合光反向传播时,i(kp+kc)·v可以忽略,由于多普勒展宽(约500 MHz)远大于5D5/2态的自然线宽,所以不需要很强的耦合光就可以获得EIT信号.
EIT谱线线型与信噪比和探测光与耦合光的扫描方式有关,通常情况下,人们采用探测光扫描方式,EIT谱存在一个多普勒背景[29].我们小组采用探测光锁定、耦合光扫描的方式,得到的EIT谱在一个平坦的背景上[36],提高了光谱的分辨率.探测光与耦合光的偏振组合同样对EIT谱线线型影响很大[31,37],实验中我们选取耦合光与探测光为水平偏振组合,避免85Rb原子激发态5D5/2超精细结构(F′′=3,4)的谱淹没在背景中.
在均为水平偏振的探测光与耦合光反向传输、探测光锁定、耦合光扫描的情况下,我们主要研究探测光与耦合光光强对阶梯型能级系统EIT谱线线型的影响.
图3为EIT谱线随耦合光功率变化的典型结果.由于探测光锁定在5S1/2(F =3)-5P3/2(F′=4)循环跃迁上,所以此时没有单共振光抽运效应,谱线信号为双共振光抽运效应与原子相干效应的叠加.耦合光较强时(图3(a)),由于功率展宽等因素的影响,EIT谱的线宽较宽,谱线交叠效应比较明显,其中(F′′=5)谱的尖峰为EIT信号,背景为双共振光抽运信号.耦合光较弱时,原子相干效应较弱,5D5/2态超精细结构(F′′=3,4)信噪比很低.

图3 (网刊彩色)EIT谱线随耦合光功率变化 探测光功率为20µW,耦合光分别为(a)2.7 mW,(b)100µW,(c)50µWFig.3.(color online)The EIT spectra according to the coupling light,the power of probe light is 20µW,the coupling light are(a)2.7 mW,(b)100µW,(c)50µW,respectively.
图4为EIT谱线随探测光功率变化的典型结果.探测光较强时(图4(a)),原子相干效应较弱,谱线区分度较差.探测光较弱时,部分谱线淹没在背景噪声里,谱线信噪比较差.

图4 (网刊彩色)EIT谱线随探测光功率变化 耦合光为100µW,探测光分别为 (a)150µW,(b)20µW,(c)5µWFig.4.(color online)The EIT spectra according to the probe light,the power of coupling light is 100µW,the probe light are(a)150µW,(b)20µW,(c)5µW,respectively.
由图3和图4的实验结果可见,探测光功率为20µW、耦合光功率为100µW时,阶梯型能级系统EIT谱信噪比最高,超精细结构区分明显,与(5)式的线型一致.实验中所用的激光器线宽约为500 kHz,如果利用线宽更窄的激光器,谱线线宽会变窄,更容易提取超精细结构信息.
频率校准系统主要包括EOM和CFP,其中EOM由锁定在铷钟上的频率综合器(Agilent 8257D)驱动,铷钟的精度为±5×10−11,稳定度<5×10−12.776 nm激光被EOM调制,通过探测调制激光束的透射峰,得到频率校准信号.
4 结果与讨论
在得到了高信噪比的EIT谱和相应的频率校准信号后,我们可以提取超精细结构的信息,典型的结果如图5所示,对应跃迁为5S1/2(F=3)-5P3/2(F′=4)-5D5/2(F′′=3,4). 横轴利用载频与+1级边带之间的频率间隔9.000 MHz标定,为了减少频率扫描非线性的影响,我们通过调节CFP腔长,将频率校准信号与EIT谱信号峰对齐.EIT谱信号和频率校准信号都由多峰Voigt函数拟合(95%置信区间).类似地,对于5S1/2(F=3)-5P3/2(F′=4)-5D5/2(F′′=4,5)跃迁,我们利用同样的方法,不同的是载频与−1级边带之间的频率间隔为9.440 MHz.

图5 (网刊彩色)85Rb原子5D5/2态超精细分裂典型测量结果 上面的曲线为EIT谱,下边的曲线为经EOM调制后的CFP的透射信号(调制频率9.000 MHz,即主频与一级边带之间的频率间隔为9.000 MHz);一级边带旁边的小峰为二级边带Fig.5.(color online)The typical measurement of the hyperfine splittings of the85Rb 5D5/2state.The upper curve is the EIT spectra,the lower curve is the transmission signals of the CFP which is modulated by the EOM(the modulation frequency is 9.000 MHz,therefore the frequency interval between the carrier and the 1-order sidebands are 9.000 MHz).The small peaks near the 1-order sidebands are the 2-order sidebands.
为了减小实验误差,我们对超精细分裂进行1000多次测量,计算得到相应的超精细分裂分别为(9.048±0.008)MHz和(9.512±0.008)MHz.参考之前的工作[8−10],我们对实验存在的系统误差进行了分析,结果列于表1,其中∆E43与∆E54分别代表85Rb原子5D5/2态(F′′=4)与(F′′=3)以及(F′′=5)与(F′′=4)之间的超精细分裂.
由(3)式可以将超精细分裂写成如下超精细相互作用常数函数的形式∶

最终,我们得到了85Rb原子5D5/2态的磁偶极超精细相互作用常数(A=(−2.222±0.019)MHz)与电四极超精细相互作用常数(B=(2.664±0.130)MHz),这与之前的结果(表2)一致,但更加精确.

表1 85Rb原子5D5/2态超精细结构误差分析(单位:kHz)Table 1.Uncertainty budget in measurement of the hyperfine structure of85Rb 5D5/2state(units:kHz).

表2 85Rb原子5D5/2态超精细相互作用常数(单位:MHz)Table 2.Hyperfine coupling constants of the 5D5/2state for85Rb(units:MHz).
5 结 论
我们研究了室温下85Rb原子5S1/2-5P3/2-5D5/2阶梯型能级系统激发态EIT光谱.水平偏振的探测光与耦合光反向传输,较弱的探测光锁定在5S1/2(F=3)-5P3/2(F′=4)跃迁上,较强的耦合光在5P3/2态到5D5/2态之间扫描,得到的EIT光谱具有平坦的背景,通过选取光强合适的探测光和耦合光,获得了高信噪比的EIT光谱,这不仅可以用来更好地提取超精细结构的信息,而且还可以更好地帮助我们理解不同进程对原子相干效应的影响,比如原子弛豫和碰撞、光抽运、多普勒展宽等[38].在频率校准时,为了减少频率扫描非线性的影响,我们将EOM调制的CFP信号与EIT谱信号对齐,得到了85Rb原子5D5/2态超精细分裂(∆E43=(9.048±0.056)MHz)与(∆E54=(9.512±0.052)MHz),最终经计算获得了85Rb原子5D5/2态的磁偶极超精细相互作用常数(A=−(2.222±0.019)MHz)与电四极超精细相互作用常数(B=(2.664±0.130)MHz).这与之前的结果保持一致[3−5,7],但更加精确.这对D态原子超精细结构计算及宇称不守恒测量都具有重要的参考意义.
[1]Wood C S,Bennett S C,Cho D,Masterson B P,Roberts J L,Tanner C E,Wieman C E 1997 Science 275 1759
[2]Dzuba V A,Flambaum V V,Ginges J S M 2001 Phys.Rev.A 63 062101
[3]Nez F,Birabenf1993 Opt.Commun.102 432
[4]Nez F,Biraben F,Felder R,Millerioux Y 1994 Opt.Commun.110 731
[5]Grove T T,Sanchez-Villicana V,Duncan B C,Maleki S,Gould P L 1995 Phys.Scr.52 271
[6]Stalnaker J E,Mbele V,Gerginov V,Fortier T M,Diddams S A,Hollberg L,Tanner C E 2010 Phys.Rev.A 81 043840
[7]Gabbanini C,Ceccherini F,Gozzini S,Lucchesini A 1999 Meas.Sci.Technol.10 772
[8]Yang G,Wang J,Yang B D,Wang J M 2016 Laser Phys.Lett.13 085702
[9]Wang J,Liu H F,Yang B D,He J,Wang J M 2014 Meas.Sci.Technol.25 035501
[10]Wang J,Liu H F,Yang G,Yang B D,Wang J M 2014 Phys.Rev.A 90 052505
[11]Harris S E,Field J E,Imamoğlu A 1990 Phys.Rev.Lett.64 1107
[12]Ham B S,Shahriar M S,Hemmer P R 1997 Opt.Lett.22 1138
[13]Hakuta K,Suzuki M,Katsuragawa M,Li J Z 1997 Phys.Rev.Lett.79 209
[14]Zibrov A S,Lukin M D,Scully M O 1999 Phys.Rev.Lett.83 4049
[15]Li X L,Liu H N,Yang Y 2011 Acta Opt.Sin.31 0102001(in Chinese)[李晓莉,刘红娜,杨悦 2011光学学报 31 0102001]
[16]Boller K J,Imamoğlu A,Harris S E 1991 Phys.Rev.Lett.66 2593
[17]Field J E,Hahn K H,Harris S E 1991 Phys.Rev.Lett.67 3062
[18]Padmabandu G G,Welch G R,Shubin I N,Fry E S,Nikonov D E,Lukin M D,Scully M O 1996 Phys.Rev.Lett.76 2053
[19]Ham B S,Shahriar S M,Hemmer P R 1999 J.Opt.Soc.Am.B 16 801
[20]Hopkins S A,Usadi E,Chen H X,Durrant A V 1997 Opt.Commun.138 185
[21]Hau L V,Harris S E,Dutton Z,Behroozi C H 1999 Nature 397 594
[22]Lvovsky A I,Sanders B C,Tittel W 2009 Nature Photon.3 706
[23]Bajcsy M,Zibrov A S,Lukin M D 2003 Nature 426 638
[24]Lee M J,Ruseckas J,Lee C Y,Kudriasov V,Chang K F,Cho H W,Juzeliunas G,Yu I A 2014 Nature Commun.5 5542
[25]Kuzmich A,Bowen W P,Boozer A D,Boca A,Chou C W,Duan L M,Kimble H J 2003 Nature 423 731
[26]Ottaviani C,Vitali D,Artoni M,Cataliotti F,Tombesi P 2003 Phys.Rev.Lett.90 197902
[27]Kominis I K,Kornack T W,Allred J C,Romalis M V 2003 Nature 422 596
[28]Zhao J M,Zhu X B,Zhang L J,Feng Z G,Li C Y,Jia S T 2009 Opt.Express 17 15821
[29]Banacloche J G,Li Y Q,Jin S Z,Xiao M 1995 Phys.Rev.A 51 576
[30]Boon J R,Zekou E,McGloin D,Dunn M H 1999 Phys.Rev.A 59 4675
[31]Moon H S,Lee L,Kim J B 2005 J.Opt.Soc.Am.B 22 2529
[32]Foot C J 2005 Atomic Physics(New York:Oxford University Press)
[33]Johnson W R 2007 Atomic Structure Theory:Lectures on Atomic Physics(New York:Springer)
[34]Han Y S,Guo S L,Wang J,Liu H F,He J,Wang J M 2014 Chin.Opt.Lett.12 121401
[35]McCarron D J,King S A,Cornish S L 2008 Meas.Sci.Technol.19 105601
[36]Yang B D,Gao J,Zhang T C,Wang J M 2011 Phys.Rev.A 83 013818
[37]McGloin D,Dunn M H,Fulton D J 2000 Phys.Rev.A 62 053802
[38]Ye C Y,Zibrov A S 2002 Phys.Rev.A 65 023806
PACS∶32.10.Fn,42.50.Gy,42.50.HzDOI∶10.7498/aps.66.103201
*Project supported by the National Natural Science Foundation of China(Grant Nos.61475091,11274213,61227902).
†Corresponding author.E-mail:wwjjmm@sxu.edu.cn
Determination of the hyperfine coupling constants of the 5D5/2state of85Rb atoms by using high signal-to-noise ratio electromagnetically-induced transparency spectra∗
Yang Guang1)2)Wang Jie1)2)Wang Jun-Min1)2)3)†
1)(Institute of Opt-Electronics,Shanxi University,Taiyuan 030006,China)
2)(State Key Laboratory of Quantum Optics and Quantum Optics Devices,Shanxi University,Taiyuan 030006,China)
3)(Collaborative Innovation Center of Extreme Optics,Taiyuan 030006,China)
16 January 2017;revised manuscript
3 March 2017)
We report the hyperfine splitting measurement of the85Rb 5D5/2state by electromagnetically induced transparency spectroscopy with high signal-to-noise ratio in the85Rb 5S1/2-5P3/2-5D5/2ladder-type system(780 nm+776 nm).The frequency calibration is performed by employing a phase-type electro-optic modulator with a confocal Fabry-Perot cavity.From the measured hyperfine splittings among the manifolds of(F′′=5),(F′′=4)and(F′′=3)of the85Rb 5D5/2state,we determine the magnetic dipole hyperfine coupling constant(A=(−2.222±0.019)MHz)and the quadrupole coupling constant(B=(2.664±0.130)MHz)of 5D5/2state of85Rb atoms.
∶hyperfine splitting,electromagnetically-induced transparency,electronic-optic modulator,Fabry-Perot cavity
∗国家自然科学基金(批准号:61475091,11274213,61227902)资助的课题.
†通信作者.E-mail:wwjjmm@sxu.edu.cn
©2017中国物理学会Chinese Physical Society
