多面转镜激光器扫频光学相干层析成像系统的全光谱重采样方法∗

樊金宇 高峰 孔文 黎海文 史国华

(中国科学院苏州生物医学工程技术研究所,江苏省医用光学重点实验室,苏州 215163)

多面转镜激光器扫频光学相干层析成像系统的全光谱重采样方法∗

樊金宇 高峰 孔文 黎海文 史国华†

(中国科学院苏州生物医学工程技术研究所,江苏省医用光学重点实验室,苏州 215163)

(2016年11月25日收到;2017年4月9日收到修改稿)

在多面转镜激光器扫频光学相干层析成像系统中,激光器存在着输出光谱错位与扫频范围波动的问题.目前的重采样方法中,普遍利用互相关运算校正光谱错位,并进行大范围的截取,保证扫频范围的一致性,但这会导致成像信噪比与分辨率的降低.本文用马赫-曾德尔干涉仪(MZI)采集到的干涉信号对扫频范围波动的问题进行了详细的测量与分析,其中干涉信号的解缠相位曲线的非随机性和平行性,表明该类激光器输出光谱的波长分布具备一致性.在此基础上,提出了一种用最长扫频范围的MZI干涉信号,对样品干涉信号进行时域光谱对齐、然后进行一对多插值的重采样方法.实验与分析表明,该方法利用了所有的光谱信号,保证了样品干涉信号的能量利用率,能有效提高图像的信噪比与分辨率.

多面转镜扫频激光器,扫频范围,重采样,信号利用率

1 引言

光学相干层析成像(optical coherence tomography,OCT)技术通过测量组织后向散射光的低相干干涉信号进行断层成像,在眼科成像、肿瘤检测、手术导航等领域有广泛的应用.其第三代扫频光源光学相干层析成像(swept-source optical coherence tomography,SS-OCT)技术有更高的灵敏度、更加宽泛的成像波段,受到冲刷效应的影响也较小[1,2],已逐步成为OCT的主流应用形式.

在SS-OCT中,扫频激光器直接决定成像系统的性能.扫频激光器分为短腔型和长腔型.傅里叶域锁模技术是长腔型的代表技术,但该技术需用到几公里的长光纤[3],成本较高且稳定性差.因此目前应用主流是短腔型激光器.其中多面转镜激光器利用光栅进行分光,用镜面和光束间的角度进行选频[4],其整体波长分布较为稳定[5],有较长的自由光谱范围[6],是目前最为常用的短腔型激光器.然而各个镜面的几何转轴、面型以及同步触发信号的不一致性,导致输出光谱的局部不稳定(包括光谱错位和扫频范围波动).因此,解决该类不稳定现象是提高SS-OCT成像质量的关键.

潘聪等[7]利用界面信号提取光谱错位形成的偏移量并对齐干涉信号,但是要求光源输出光谱有较低的错位量.Liu等[8]和Braaf等[9]分别利用固定模式噪声处的相位信息和马赫-曾德尔干涉(MZI)信号的互相关函数对齐干涉信号,但也只能矫正自相关信号2π内的偏移量,而且这些方法是在波数空间进行的.因此,上官紫薇等[10]在时域空间内对干涉信号解缠相位进行互相关运算,矫正了大范围的光谱偏移.但是,在时域空间依然存在亚采样间隔的错位,需要对特定截取的信号区域插值后才能完全对齐.国内外对光谱错位的现象已开展了较深入的研究,而扫频范围波动的问题,国际范围内并没有对其进行详细分析,大都采用截取固定扫频范围的方法,直接导致SS-OCT系统信噪比与分辨率的降低.

本文详细分析了多面转镜激光器扫频范围波动的现象及其对重采样的影响,提出一种无需截取有效信号的一对多重采样方法.该方法基于多面转镜整体波长分布较为稳定的特点,在互相关运算和平移前对干涉信号进行了内插扩展,在下采样中得到了对齐的干涉信号,并利用扫频范围最大的MZI干涉信号对其进行插值.实验与分析表明,该方法能利用到原有重采样方法中被排除的有效信号,提高了样品干涉信号的能量利用率和图像信噪比,同时有较高的重采样精度.

2 多面转镜型激光器不稳定评估以及对重采样的影响

2.1 系统搭建

如图1所示,本文选择了两台不同型号的典型多面转镜型激光器进行测试,型号分别为HSL-2000(中心波长λ=1315 nm,光谱带宽∆λ=110 nm,20 kHz)和HSL-2100-HW(λ0=1315 nm,∆λ=140 nm,50 kHz),系统采用商用的光纤型迈克耳孙干涉仪(Thorlabs,INT-MSI-1300).为了对波长范围变化进行测量和干涉信号的重采样,引入了光纤型马赫-曾德尔干涉仪(Thorlabs,INTMZI-1300).根据两台激光器扫频速度的不同,分别使用NI PCI5122(最大采样率100 MHz,实验采样率50 MHz)和ATS9350(最大采样率500 MHz,实验采样率200 MHz),采集两台激光器的迈克耳孙(MSI)干涉信号和MZI干涉信号.

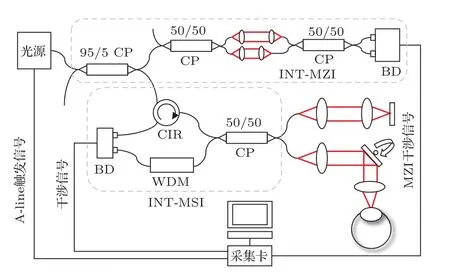
图1 SS-OCT系统结构图CP,耦合器;CIR,环形器;BD,平衡探测器;WDM,波分复用器Fig.1.Setup of SS-OCT:CP,coupler;CIR,circulator;BD,balance detector;WDM,wavelength division multiplexer.

2.2 光谱错位测量

在分析扫频范围波动之前,需要测量激光器的光谱错位量.通过对MZI干涉信号做互相关运算,提取时域空间的光谱偏移量.由于两种光源各测量参数的分布较为相似,本文仅展示了HSL-2000的测量结果图;光谱错位量分布如图2所示,其中正负分别代表待测光谱超前和滞后参考光谱.其中HSL-2000有高达50个点(1µs)的偏移量,HSL-2100-HW偏移量也高达40个点(0.2µs).

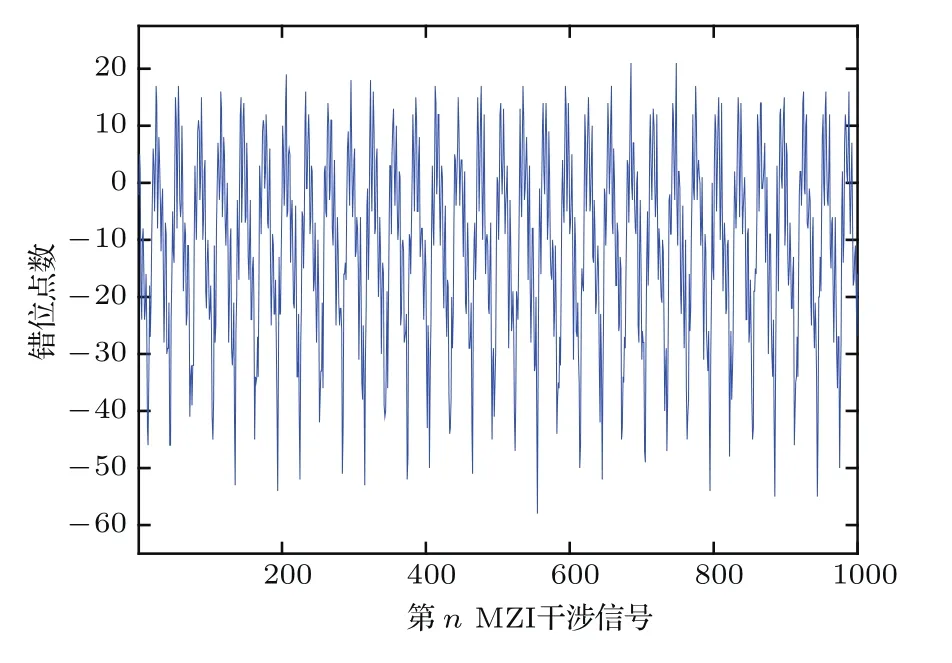
图2 利用互相关提取出的时域上的MZI干涉信号之间的光谱偏移量,光源为HSL-2100-HW时测得Fig.2.The o ff set between MZI signals obtained using cross correlation in the time domain when using the laser HSL-2000.

2.3扫频范围测量

在多面转镜激光器中,不同扫频周期由不同的镜面进行选频后,随时间输出波长序列.但是,各个镜面的几何位置和镀膜质量不一致,会导致返回光增益介质的选频光功率不稳定,从而引起扫频范围的改变,具体表现为两端本该输出的波段消失.在分析激光器扫描范围波动对SS-OCT成像影响时,需要对波数范围的波动量进行测量,而扫频激光器输出的光谱信号在波数空间通常是非均匀的,因此要用到MZI干涉信号描述时间序列和波数序列的关系(有些扫频光源提供等波数间隔的采集触发信号,由K-trigger端口输出,但其本质上也是由MZI和检测电路产生).MZI干涉干涉条纹可以描述为

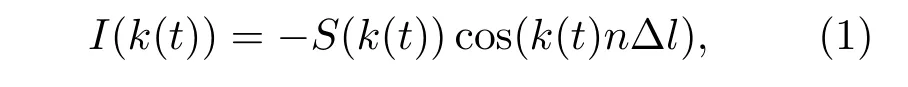
其中∆l为MZI两臂间的光程差(本系统中为2 mm),k为波数,t为时间,S(k(t))为光功率谱.从(1)式中得知,在光程差和折射率不变的情况下,MZI干涉信号的相位和波数是线性关系.因此,可以通过比较不同扫频周期采集到的MZI干涉信号的相位信息来得到波数范围的相对变化量.MZI干涉信号的相位信息可以通过希尔伯特变换后的解析扩展的辐角得到

对不同扫频周期采集到的两组MZI干涉信号进行波长对齐(光谱错位测量见2.2节,干涉信号对齐步骤见第3部分)并计算其相应的解缠相位曲线.如图3(a)所示,相位曲线上升段即为MZI干涉信号的有效区域.因此,只需要比较相位曲线的总相位变化量∆φ,就可以得出光谱信号在波数域的相对变化量.

图3(b)展示了HSL-2000光源1000条MZI干涉信号在波长和波数域的跨度分布.HSL-2000输出的波长和波数空间的范围变化分别为7.76%和7.16%,平均值为1876个采样点和1193.1 rad.HSL-2100-HW输出的波长和波数空间的范围变化分别为7.02%和4.53%,平均值为2955个采样点和2948.9 rad.从图3中可以看出扫频范围是呈周期性变化的.

所有波长对齐后的MZI干涉信号的相位曲线绘制在图4(a)中,同时在时域选取了任意位置(图中红竖线处),在图像右下方绘制了其相位分布.可以看到HSL-2000光源1000条MZI干涉信号相位曲线集中的分布在8条曲线中.HSL-2100-HW光源1000条MZI干涉信号相位曲线则分布在18条曲线中.相位曲线具有的周期性和重复性表明扫频范围的变化是多面转镜各个镜面周期性扫频所引起的.相位曲线分布的平行性也说明激光器输出光谱波长和波数的分布较为一致,在共同有效信号区域用一条相位曲线即可表示所有光谱信号的波数分布.

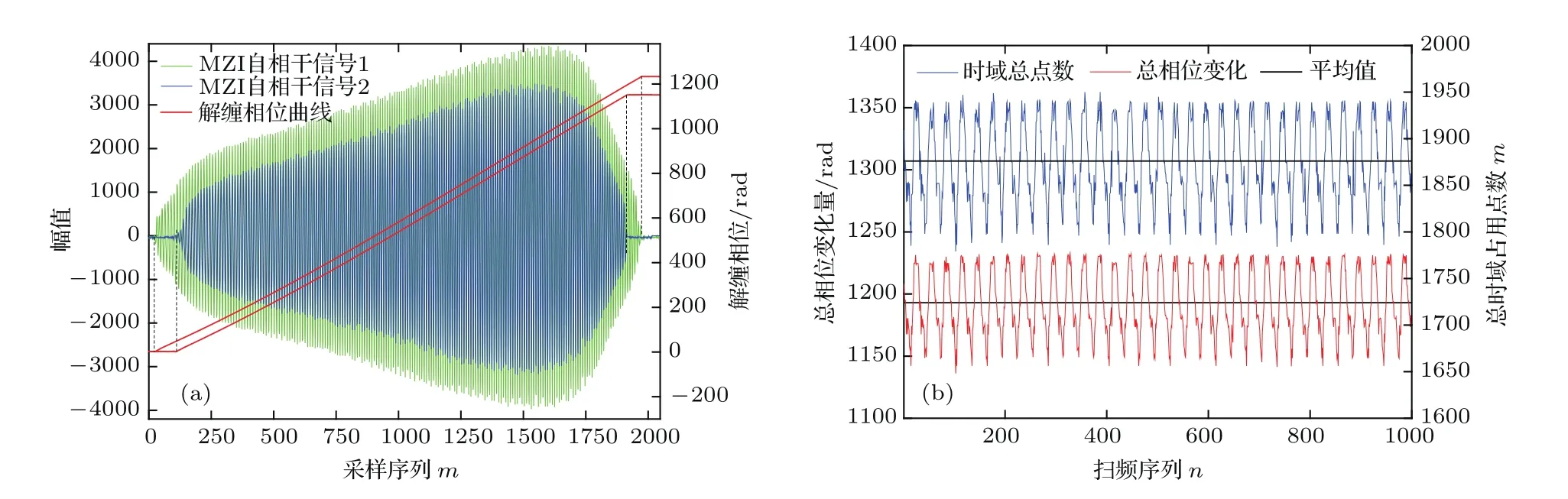
图3 (网刊彩色)(a)扫频范围不同情况下的MZI干涉信号与相应的解缠相位曲线;(b)MZI干涉信号的时域信号占总点数分布和相位总变化量分布及其相应的平均值,数据来自于HSL-200Fig.3.(color online)(a)MZI signals with di ff erent sweep range and the corresponding unwrapped phase curve;(b)MZI signals’total pixels in time domain and the distribution of the phase increment.The data obtained when using the laser HSL-2000.

图4(网刊彩色)(a)1000条对齐后MZI干涉信号的解缠相位曲线的局部放大图和竖线处的相位分布(内插图);(b)解缠相位曲线整体图,有最大扫频范围MZI干涉信号的相位曲线由红色曲线标注;数据来自于HSL-2000激光器Fig.4.(color online)(a)1000 MZI signals’unwrapped phase curves and the phase distribution at speci fi c position(red vertical line);(b)phase curves that has largest swept range was marked by red curve.The data obtained when using the laser HSL-2000.

图4 (b)绘出了整体的解缠相位图,从图中可知,最大扫频范围MZI干涉信号的解缠相位信息同时也包含所有其他已对齐MZI干涉信号的解缠相位信息,因此可以认为最大扫频范围包含了所有波段.

3 数据处理

在对MSI低相干干涉信号进行波数重采样时,需要利用MZI干涉信号的解缠相位曲线进行等相位间隔插值[11,12].相位间隔大小由插值点数和相位曲线总增量∆φ确定.而样品深度信息由波数空间干涉信号的离散傅里叶变换得到,由离散傅里叶变换的性质可知,深度Z空间的分辨率和总相位的关系可以描述为

在激光器扫频范围变化,导致相位曲线总增量改变的情况下,深度分辨率∆z会随着∆φ的波动而改变,即不同干涉信号有不同的尺度,最终导致图像的错位.但是较短的MZI干涉信号的两端相位信息缺失.因此,在先前报道的重采样方法中[8−10],利用MZI干涉信号对相应的MSI干涉信号进行插值前,对信号进行了大范围的截取.

经过本文第2部分对激光器的测量,发现多面转镜型激光器的整体波长分布较为稳定,且其相位曲线分布的平行性也说明激光器输出光谱波长的分布较为一致.因此,本文提出直接用有最长扫频范围的MZI干涉信号的相位信息对所有的MSI干涉信号进行插值的方法,从而最大程度地提高系统信噪比和分辨率.

3.1 算法流程

由上述可知,在扫频范围波动的情况下,通常重采样过程中必须经过截取(图5(a)区域1处信号被排除),以保证最终得到的待重构MSI干涉信号有相同的波数范围.但是在光谱错位的情况下,在时域(波长域)进行截取会导致部分有效信号被排除(图5(a)区域2处的信号),而且截取到的干涉信号波数范围也不同:

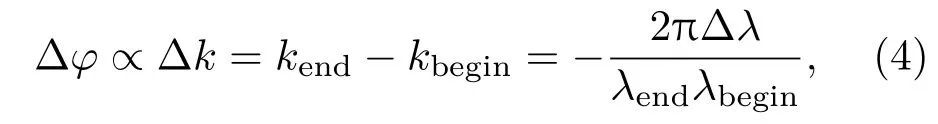
其中kend,kbegin分别是截取后光谱结束和开始的波数;λend,λbegin分别是结束和开始的波长.尽管截取后有相同的波长变化量∆λ,但是光谱错位导致的不同λend,λbegin还是会使MSI干涉信号有不同的波数范围∆k以及总相位增量∆φ.为得到波数范围相同且完全对齐的干涉信号,文献[10]中以时域粗矫正后的相位曲线的初始相位为基准,得到亚像素点的偏移量,划定每条干涉信号的插值区域,继而用所有MZI干涉信号对相应MSI干涉信号进行一对一插值,完成了等相位增量截取(流程如图5(b)所示).

图5 (网刊彩色)(a)扫频范围的不同(上)和光谱的错位(下)分别导致区域1和区域2的有效信号在截取中被排除;(b)文献[10]中的方法和(c)本文提出的方法处理流程对比Fig.5.(color online)(a)Interference signal in area 1 and 2 will be excluded in truncation when there are fl uctuation in wavenumber(top)and spectral misplacement(bottom),respectively;(b)Ding et al.’s method[10]and(c)proposed method.

因此,在文献[10]的方法中,至少需要排除图5(a)区域1的信号,对于光源HSL-2000,至少6.91%波数范围的干涉信号无法利用,对于光源HSL-2100-HW,至少4.17%波数范围的干涉信号无法利用.这将会降低信号的能量利用率,具体的衰减值和被排除信号的有效性验证将在实验部分展示.同时由(3)式可知,总相位增量∆φ的降低还会引起图像深度方向分辨率的下降.

本文提出的方法在时域即完成了干涉信号的对齐(见3.2节),在任意相同时间段的干涉信号都有相同的波数范围,扫频范围最长的MZI干涉信号的相位信息又包括了所有波段.因此,只需对最长扫频范围的MZI干涉信号相位信息进行一次拟合,即可完成对所有MSI干涉信号的插值(图5(c)所示),从而在简化了处理流程的同时,又无需排除有效信号,最终提高了MSI干涉信号的利用率和图像分辨率.

3.2 光谱错位矫正

除了导致总相位增量不一致,光谱的错位还会影响到插值的准确性,因此在插值之前需要在时域对齐MSI干涉信号.考虑到多面转镜激光器整体波长分布较为稳定,不会造成MZI干涉信号形变,因此对齐的偏移量由MZI干涉信号间的互相关运算得到.但是光谱错位在时域的延时并不是采样间隔时间的整数倍,经过整数个采样点的平移并不能使干涉信号在时域完全对齐:根据离散傅里叶变换的时移特性,光谱错位量ms和在频率(深度)z处引入的相位误差∆φmisplace可以由

表示,其中N为总点数.经过整数倍的平移矫正后,依然可能存在ms=1/2(采样间隔的一半)的偏移量,因此剩余的相位误差

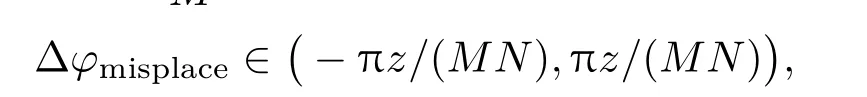
降低了剩余相位误差的范围.因此可以通过提高采集设备的采样率提高对齐精度,但是该方法对硬件的要求也更高.为了在不增加系统复杂度的情况下提高对齐的精度,对所有MZI干涉信号和MSI干涉信号进行了频域补零插值扩展:

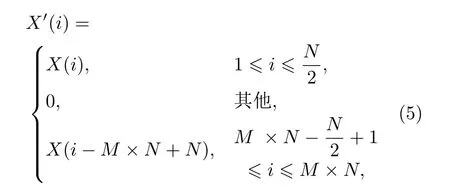
其中X(i)为原始序列的离散傅里叶变换,N为单个干涉信号的总像素点,M为扩展倍数.在对序列X′(i)进行离散傅里叶逆变换即可得到M倍扩展后的新序列.然后用互相关算法提取所有MZI干涉信号相对最长扫频范围的MZI干涉信号的偏移量,对扩展后的MSI干涉信号进行平移,再进行扩展倍数间隔的下采样即可得到原信号长度的时域对齐干涉信号.

通过比较平移后的MZI干涉信号和扫频范围最长的MZI干涉信号的相位差可以得到提取的偏移量的精度.图6展示了不同扩展倍数下MZI干涉信号相位变化的标准差.可以看到,扩展倍数从2倍到16倍,相位变化的标准差大大减小,在40倍以上趋于稳定.

图6 相关算法中扩展倍数与相位差的关系以及拟合曲线Fig.6.Phase di ff erence and the corresponding extension multiple and the fi tted curve.

此时,所有时域干涉信号都与扫频范围最长的MZI干涉信号波数对齐,在时域任意有效信号区域,不同MSI干涉信号都在时域上有相同的波数分布和波数范围.

3.3 一对多插值过程描述

在时域完成MSI干涉信号的光谱矫正后,以相邻点相位差分最大的两处为上下界,即可确定扫频范围最长MZI干涉信号的有效信号区域(图7(a)所示)与相位总增量∆φ.对该段信号的解缠相位曲线进行9阶多项式拟合(系数如表1所列),等相位间隔取值得到插值位置并利用(6)式计算插值系数(其中i为插值索引,s′为插值位置,插值总点数N=2048,总相位增量∆φ=1214.8 rad,截断加权系数长度L=21),再通过(7)式对所有MSI干涉信号进行内插[13]即可完成一对多的重采样过程(如图7(b)所示).

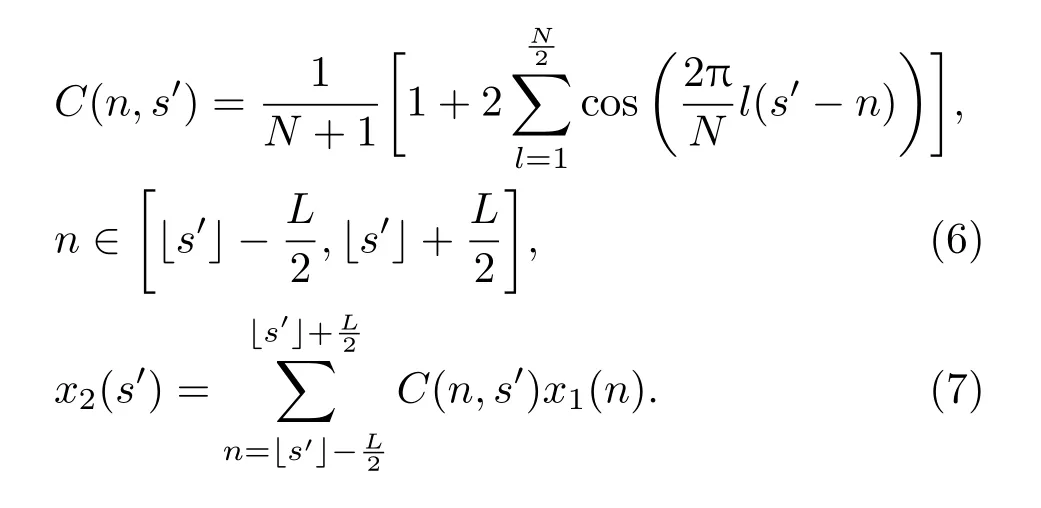
表1 对有效区域MZI干涉信号解缠相位多项式拟合的系数Table 1.Polynomial fi tting coefficient for the unwrapped phase of the MZI signal.

图7 (网刊彩色)(a)解缠相位与相邻相位差曲线;(b)用最长扫频范围MZI干涉信号对所有MSI干涉信号插值示意图Fig.7.(color online)(a)Unwrapped phase curve and its di ff erences;(b)interpolation of MSI signals using unwrapped curve of MZI signal that has largest swept range.

4 实验与结果

本文通过对多面转镜激光器输出信号的分析,指出了扫频范围波动和光谱错位的规律.基于其MZI干涉信号相位曲线的平行性,提出了用最长扫频范围的MZI干涉信号,对所有MSI干涉信号一次性进行重采样的方法.为了验证本文提出的重采样方法的性能,进一步开展了实验研究.利用多层盖玻片的MSI干涉信号进行了截取衰减实验,分析了对成像信噪比的影响.然后,以静止平面镜为样品,对采集到的20000条MSI干涉信号镜面深度的相位差进行了统计分析,以验证重采样过程中的对齐精度和插值精度.

4.1 信号截取实验

实验中选择多层盖玻片为样品,以引入不同频率分量,并对同一横向位置同步采集了1000条干涉信号(MZI干涉信号与MSI干涉信号).为了分析不同截断长度下对信噪比的影响,将最短的MZI干涉信号作为参考,对MSI干涉信号进行不同截取长度下的重采样(其中在时域截取的区域设为起始索引,每次加50,结束索引减50,单边阈值直至700,共14个截取长度),从而得到傅里叶变换后100个峰值的平均值.

图8(a)展示了同一条MSI干涉信号分别在时域截取区域减少200点和400点时的频谱.后者各频谱分量幅值都低于前者,其中在峰值处衰减了1.05 dB.图8(b)则展示了最终获得的上述14个不同截取长度下,MSI干涉信号频谱峰值的平均值相对于原始信号频谱峰值的平均值的衰减程度.结果表明对有效信号截取会导致信号强度降低.

为了验证通常重采样中被排除信号(图5(a)区域1)的有效性,从扫频范围最大的MSI干涉信号(波数空间)中单独提取出了该段信号进行频谱分析.其在波数空间占用113个像素点,和完整信号相比(2048像素点)频谱分辨率较低,频率尺度也不同.因此需要补零至2048,并从保留区域信号(图6(a)截取区域)中任意选取了113个像素点的信号作为比较.从图9的频谱可以得知,排除区信号的极大值位置和完整信号以及保留区信号极大值位置一一对应,这说明排除区信号也具有频率(样品深度信息)分辨的能力,而本文提出的重采样方法可以充分利用该频率信息.

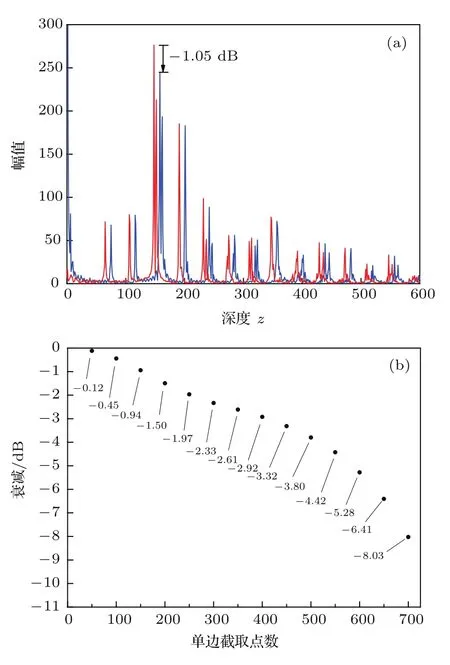
图8 (网刊彩色)(a)两端在时域分别排除200点(为了清楚地对比向左平移了10个点)和400点(右)的干涉信号频谱;(b)时域截取区域逐次减少100的峰值平均值相对于不截取信号的衰减Fig.8.(color online)(a)Depth pro fi le of truncated signal when exclude 200(left shift 10 points for clear comparation)and 400 points(right curve)in time domain;(b)fall o ffbetween signal without exclusion and signal excluded with point number.

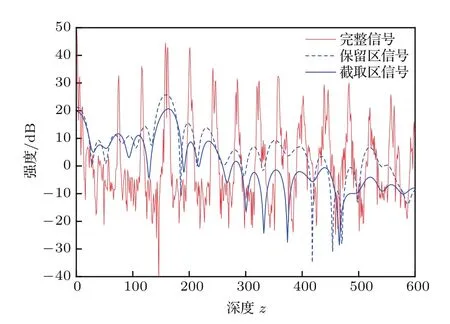
图9 (网刊彩色)多层盖玻片完整信号、保留区信号和排除区信号的频谱Fig.9.(color online)Depth pro fi le obtained from fully utilized signal,reserved signal and removed signal for multi-cover glass.

4.2 重采样精度测量与运算量评估

由上述可知,提出的重采样方法精度由光谱对齐效果和整体波数分布的稳定性决定,而波数分布稳定性同样影响互相关算法对齐光谱的精度.因此,只要得出光谱对齐的效果,即可检验本文提出重采样方法的精度.静止平面镜的干涉信号在波数域通常表示为单一频率,信号强度较大(该频率处信噪比较高)且稳定,不会引入额外的相位噪声,因此通常用于检测OCT系统的相位稳定性.而相位稳定性通常由光谱错位程度决定,为检测对齐精度,对静止平面镜同步采集了20000条干涉信号,并对光谱错位矫正后的镜面深度的相位噪声进行统计.理论上,当光谱完全对齐后,最终相位噪声由信号噪声的随机相位产生.本方法在矫正过程中利用了MZI干涉信号,因此本系统的相位噪声由MZI干涉信号和MSI干涉信号的信噪比共同决定[14−16]:

其中是相位变化量的标准差,SNRs是样品在深度Zs的信噪比,SNRc是MZI干涉信号在深度Zc的信噪比.

图1020000 条平面镜干涉信号的相位差分布Fig.10.Phase di ff erences distribution obtain from 20000 interference signals for static mirror.

根据图6,在实验中将扩展倍数设置为40.此时,该系统在平面镜深度为1.01 mm(对应第98个像素点),信噪比SNRs为49 dB,SNRc和Zc分别为56 dB与2 mm(对应第194个像素点),由(5)式得出的理论噪声为0.0036 rad,而统计出的相位噪声为0.0039 rad(图10为相位差的分布),接近理论值.说明本方法在基于多面转镜型激光器的SSOCT中对于MSI干涉信号的对齐和系统相位稳定性的提升具有极佳的效果.这也直接证明了该方法具有很高的重采样精度.需要指出的是,本文所提方法基于MZI干涉信号和MSI干涉信号是同步采集的,两者之间的不同步采集将会导致干涉信号对齐和重采样精度的下降.本系统在重采样后有较高的对齐精度,可以认为MZI干涉信号和MSI干涉信号是同步采集的.

40倍的扩展将会占用大量的内存和计算时间,因此在通常的成像处理过程中将选用较低的扩展倍数.当扩展倍数为8时,上述20000静止平面镜干涉型号的相位噪声为0.0177 rad,足以用于通常的成像处理.由于文献[10]没有给出插值的运算时间和运算量,本文在同样的数据大小、插值方法[13]和插值参数下(插值点数N=2048,截断加权系数长度L=21,一帧图像干涉信号数量A=1280,扩展倍数M=8,64)对两种方法主要步骤所需的实数乘法数量进行了对比,见表2.

表2 主要运算步骤实数乘法数量的对比Table 2.Multiplication number of main process step in di ff erent method.

相较于文献[10]的处理方法,由于需要信号扩展,曲线对齐过程运算速度较慢,但是无需对所有MZI信号进行标定、对插值系数进行重复计算的特点使得运算量大大降低.从表2可知,本文提出的方法在64倍扩展下所需乘法运算量依然低于文献[10]中方法的乘法运算量.评估中还不包括文献[10]一对一插值过程中更多的离散希尔伯特变换、相位曲线拟合等的运算量.

在经过GPU并行加速后,提出的重采样方法在56.10 s即完成了500帧上述干涉信号的处理,平均每秒处理8.9帧(8倍扩展;CPU:Intel i7-4790K,4 GHz;GPU:NVIDIA Tesla C2075;RAM:32 GB).

4.3 成像实验

图11(a)展示了利用所有MZI干涉信号对相应MSI干涉信号不进行截取、并一对一重采样后获得的柚子果肉图像.可以看到,虽然该方法也能最大限度地利用干涉信号,但是由于扫频范围的波动,导致图像轴向分辨率和深度尺度的改变,最终造成图像失真(细胞壁结构扭曲).由(3)式和2.3节测出的波数范围波动量可知,图像深度方向错位量为7.16%.

图11 柚子果肉结构图成像经过(a)不同波数范围的重采样;(b)改进型重采样(8倍扩展),其中参考信号为波数范围最大的MZI干涉信号Fig.11.Pomelo fruit fl esh intensity image obtain from when(a)implement resampling with di ff erent wavenumber increment,(b)use proposed resampling method.

图11(b)展示了采用本文提出的方法在8倍扩展的情况下获取的柚子果肉图像.可以看到利用扫频范围最长MZI干涉信号对MSI干涉信号,一对多进行重采样后,可以全面利用干涉信号的能量,提高成像的信噪比,同时重采样后的干涉信号都有相同的波数范围,不会造成样品结构失真.

5 结论

本文针对多面转镜激光器的输出光谱错位与扫频范围波动问题,开展了详细的测量与分析.通过对两台典型多面转镜激光器的输出光谱测量后,明确了该种类型的激光器在矫正光谱错位后,其各镜面面型不一致引入的扫频范围波动的解缠相位曲线具有一致的波长分布.从而提出了一种可以用最长扫频范围的MZI干涉信号,对MSI干涉信号进行一对多插值的重采样方法.相较于前期报道的方法,本文在不截取干涉信号的同时,解决了多面转镜激光器的光谱错位与扫频范围波动的难题.理论分析与样品实验表明,该方法在时域就可以完成信号的光谱对齐,提高了光谱错位矫正的效率;同时在重采样过程中无需对MSI干涉信号的有效区域进行截取,提高了样品干涉信号的能量利用率,提升了图像的信噪比与分辨率.

[1]Yun S H,Tearney G,de Boer J F,Bouma B 2003 Opt.Express 12 2977

[2]You J W,Chen T C,Mujat M,Park B H,de Boer J F 2006 Opt.Express 14 6739

[3]Chen M H,Ding Z H,Wang C,Song C L 2013 Acta Phys.Sin.62 068703(in Chinese)[陈明惠,丁志华,王成,宋成利2013物理学报62 068703]

[4]Yun S H,Boudoux C,Tearney G J,Bouma B E 2003 Opt.Lett.28 1981

[5]Huo T,Zhang J,Zheng J,Chen T,Wang C,Zhang N,Liao W,Zhang X,Xue P 2014 Opt.Lett.39 247

[6]Wang P H,Zhang J,Liu G J,Chen Z P 2011 SPIE BiOS.International Society for Optics and Photonics San Francisco,USA,January 22,2011 p78892Q

[7]Pan C,Guo L,Shen Y,Yan X G,Ding Z H,Li P 2016 Acta Phys.Sin.65 014201(in Chinese)[潘聪,郭立,沈毅,严雪过,丁志华,李鹏2016物理学报65 014201]

[8]Liu G J,Tan O,Gao S S,Pechauer A D,Lee B,Lu C D,Fujimoto J G,Huang D 2015 Opt.Express 23 9824

[9]Braaf B,Vermeer K A,Sicam V A D P,van Zeeburg E,van Meurs J C,de Boer J F 2011 Opt.Express 19 20886

[10]Shangguan Z W,Shen Y,Li P,Ding Z H 2016 Acta Phys.Sin.65 034201(in Chinese)[上官紫薇,沈毅,李鹏,丁志华2016物理学报65 034201]

[11]Yasuno Y,Madjarova V D,Makita S,Akiba M,Morosawa A,Chong C,Sakai T,Chan K P,Itoh M,Yatagai T 2005 Opt.Express 13 10652

[12]Gora M,Karnowski K,Szkulmowski M,Kaluzny B J,Huber R,Kowalczyk A,Wojtkowski M 2009 Opt.Express 17 14880

[13]Zhang Y D,Li X Q,Wei L,Wang K,Ding Z H,Shi G H 2009 Opt.Lett.34 1849

[14]Vakoc B J,Yun S H,de Boer J F,Tearney G J,Bouma B E 2005 Opt.Express 13 5483

[15]Choma M A,Ellerbee A K,Yazdanfar S,Izatt J A 2006 J.Biomed.Opt.11 024014

[16]Choma M A,Ellerbee A K,Yang C,Creazzo T L,Izatt J A 2005 Opt.Lett.30 1162

PACS:42.30.Wb,42.60.Mi,42.60.LhDOI:10.7498/aps.66.114204

A full spectrum resamping method in polygon tunable laser-based swept-source optical coherence tomography∗

Fan Jin-YuGao FengKong WenLi Hai-WenShi Guo-Hua†
(Jiangsu Key Laboratory of Medical Optics,Suzhou Institute of Biomedical Engineering and Technology,Chinese Academy of Sciences,Suzhou 215163,China)

25 November 2016;revised manuscript

9 April 2017)

Swept-source optical coherence tomography(SS-OCT)has high sensitivity and signalnoise ratio compare with timedomain optical coherence tomography and spectral-domain optical coherence tomography.Therefore,SS-OCT is the form of Fourier domain optical coherence tomography predominantly used in experimental research and biomedical image.However,polygon tunable laser-based SS-OCT su ff ers sweep range fl uctuation and spectral misplacement.Under certain circumstances,in the current resampling methods cross-correlation is widely used to align spectrum misplacement,and truncate A-lines in order to ensure the consistency of frequency-scanning range,which,however,degrades the image SNR and resolution.We use the Mach-Zehnder interference(MZI)signal to quantify and analyze this problem in two typical polygon tunable lasers.The periodical change of sweep range and spectrum misplacement show the instability derived from polygon mirror.The parallelism among unwrapped phase curves indicates that polygon tunable laser output spectra have consistent wavelength distributions,and thus it is suited to implement cross-correlation between MZI signals in time domain,and an unwrapped phase curve can represent the wavelength distribution of all A-lines.

According to the above conclusions,we demonstrate a resampling method in which the zero-padding interpolation and cross-correlation are used to align A-lines in time domain and eliminate the residual phase noise caused by integer shift.Then the unwrapped phase curve that has a largest sweep range is used to resample all the aligned A-lines,and the interference signals can be fully utilized.The experiments for signal truncation and Pomelo fruit fl esh indicate that the proposed method can improve image SNR but does not make the intensity image dislocated.The phase noise(3.9 mrad for a 49 dB SNR)from static mirror is close to theory limit after resampling,thus showing good phase stability and resampling precision.The proposed resampling method also needs less computational work than one-to-one resampling method because it only fi ts unwrapped phase curve and calculates interpolation coefficient once.

polygon tunable laser,sweep range,resampling method,signal utilization

10.7498/aps.66.114204

∗科技部重大科学仪器设备开发专项(批准号:2016YFF0102000)、中国科学院先导专项(批准号:XDB02060000)、中国科学院前沿科学重点研究项目(批准号:QYZDB-SSW-JSC03)、江苏省杰出青年基金(批准号:BK20060010)、国家自然科学基金(批准号:61675226,61378090)和中国科学院青年创新促进会资助的课题.

†通信作者.E-mail:ioe_eye@126.com

©2017中国物理学会Chinese Physical Society

http://wulixb.iphy.ac.cn

*Project supported by the National Instrumentation Program,China(Grant No.2016YFF0102000),the Strategic Priority Research Program of the Chinese Academy of Sciences(Grant No.XDB02060000),the Frontier Science Research Project of the Chinese Academy of Sciences(Grant No.QYZDB-SSW-JSC03),the Science Fund for Distinguished Young Scholars of Jiangsu Province,China(Grant No.BK20060010),the National Natural Science Foundation of China(Grant Nos.61675226,61378090),and the Youth Innovation Promotion Association,Chinese Academy of Sciences.

†Corresponding author.E-mail:ioe_eye@126.com