非对称型簇发振荡吸引子结构及其机理分析∗

吴天一陈小可张正娣张晓芳毕勤胜†

1)(江苏大学土木工程与力学学院,镇江 212013)

2)(镇江船艇学院,镇江 212003)

3)(江苏大学理学院,镇江 212013)

非对称型簇发振荡吸引子结构及其机理分析∗

吴天一1)2)陈小可1)张正娣3)张晓芳1)毕勤胜1)†

1)(江苏大学土木工程与力学学院,镇江 212013)

2)(镇江船艇学院,镇江 212003)

3)(江苏大学理学院,镇江 212013)

(2016年12月9日收到;2017年1月16日收到修改稿)

旨在揭示频域不同尺度耦合时非对称动力系统簇发振荡的特点及其分岔机理,并进一步揭示快子系统多平衡点共存导致的不同簇发模式及其产生原因.以经典的蔡氏振子为例,通过引入非对称控制项及周期变化的电流源,选取适当参数,构建存在频域两尺度耦合的非对称动力系统模型.当周期激励频率远小于系统的固有频率时,将整个周期激励项视为慢变参数,得到随慢变参数变化的快子系统平衡曲线及其不同的分岔点以及分岔行为.重点分析了三种不同周期激励幅值下典型的非对称簇发振荡及吸引子结构,揭示其相应的产生机理.指出外激励幅值的变化不仅会引起不同稳定平衡点吸引域的变化,也会使得慢变量穿越不同分岔点的时间间隔发生变化,导致系统产生不同形式的簇发振荡.

非对称系统,簇发振荡,分岔机理,吸引子结构

1 引言

不同尺度耦合系统的研究最早可以追溯到Poincaré研究行星轨道时提出的奇异摄动方程[1],但是直到诺贝尔奖获得者Hodgkin和Huxley建立了快慢两尺度神经元放电模型(H-H模型),成功地再现了其中的簇发放电行为,不同尺度耦合系统的复杂性才引起了学术界的高度重视[2].

所谓不同尺度耦合,指的是所考察的对象涉及多个尺度,这些尺度可以是时间上的,也可以是空间上的,当然也可以是时空尺度混合的[3].不同尺度之间的耦合,从其无量纲数学模型的形式上,大致可以分为两类,一类是时域上的,即存在不同量级向量场分量之间的耦合,另一类是频域上的,即耦合系统不同频率之间存在量级差距[4].

导致不同尺度耦合的因素不仅可能来自于真实时间上的快慢效应,如催化反应中存在不同量级的反应速率[5],也可能来自于几何上的尺度效应,如航天器中船体和太阳能帆板之间的耦合[6],输电塔线体系中塔线之间的耦合[7],还有其他诸如系统内部的物理效应、系统结构效应等[8].通过无量纲变化后,在相应的数学模型中出现不同的状态变量或其组合之间在变化速率上的量级差异[9].

不同尺度耦合动力系统通常表现为大幅振荡与微幅振荡的组合,如绳系卫星中的张弛振荡(空间上的多尺度)[10]和催化反应中的混合模态振荡(时间上的多尺度)[11].自诺贝尔奖获得者Hodgkin和Huxley建立了两时间尺度神经元模型(H-H模型)以来,这种特殊的振荡形式统一称为簇发振荡,当状态变量处于静止或微幅振荡时,称为沉寂态或静息态,而表现为大幅振荡时,则称为激发态.系统状态在沉寂态和激发态之间来回变化的振荡模式,称为簇发振荡[12].

针对不同尺度耦合动力系统,国内外学者开展了大量的研究工作.由于缺乏有效的分析方法,起初大都围绕着快慢耦合系统的模型分析、近似求解、数值仿真和实验分析等方面,直到Linzel快慢分析方法的引入,相关工作才上升到机理分析的层次[13].以Izhikevich为代表的一些学者,深入探讨了含一维慢子系统的低维耦合系统中的各种簇发振荡及其分岔机理[14].然而由于Linzel快慢分析方法仅对含一维慢变量的自治耦合系统有效,同时高维系统存在诸如高余维分岔等现象,迄今为止,相关工作大都是针对含一维慢变量及三维以内快子系统的自治耦合系统开展的,如Shimizu等[15]探讨了弱周期激励下两维BVP振子的簇发振荡,Shilnikov和Kolomiets[16]给出了两快一慢三维Hindmarsh-Rose模型中Hopf分岔下的不同簇发.近年来,针对典型的非自治系统——周期激励系统,当周期激励频率与系统固有频率之间存在量级差距,即包含频域上的不同尺度时,本课题组开展了富有成效的研究工作,提出了转换相图的分析方法,揭示了多种形式的簇发振荡及其产生机理[17−22].

必须指出的是,目前大部分工作是针对时域上的不同尺度耦合,也即快慢耦合系统开展的,如振幅调谐的簇发振荡[23],而对于频域上的不同尺度耦合,即系统含两个或以上存在量级差距的频率时的簇发振荡,研究尚不深入.同时,所考察的簇发振荡基本上含有对称结构,导致从沉寂态到激发态或从激发态返回沉寂态的形式相对单一,如旋转机械中的簇发振荡[24].为探讨存在频域两尺度耦合的非对称动力系统的复杂动力学行为,本文以经典的蔡氏振子为例,通过引入非对称结构的控制器和周期激励电流源,构建存在频域两尺度耦合的非对称动力系统模型,重点探讨不同周期激励幅值下各种典型的非对称簇发振荡的吸引子结构及其相应的产生机理.

2 数学模型

蔡氏电路由于存在丰富的非线性现象一直是广泛应用于证实许多非线性理论或控制方案的经典模型之一.为保证原系统的对称性,在其控制器的设计中,一般采用由奇次向量场决定的控制项.偶次向量场会破坏系统的对称性,如引入二次项控制器,其混沌结构存在非对称性[25],而引入非对称分段光滑的控制器时,则吸引子存在非对称多涡卷结构[26].因此考虑如下二次项控制器[16]下广义蔡氏振子的不同尺度耦合效应:

式中(x,y,z)∈R3是状态变量,u为非对称结构的反馈控制项,f(x)=−x(x2−1)(x2−β)为非线性模块,w=Asin(Ωt)为周期外激励项.当激励振幅A=0,即外激励项不存在时,自治系统((1)式)会按照其固有频率振荡.为考察频域上的不同尺度效应,取定激励频率Ω≪ω,其中ω为固有频率,此时系统((1)式)会存在各种复杂的簇发振荡现象.

3 分岔分析

当Ω≪ω时,系统((1)式)的状态变量主要按照固有频率振荡.在固有频率所对应的任一个周期T=[t0,t0+2π/ω]内,激励项w将从WA变化到WB,其中WA=Asin(Ωt0),WB=Asin(Ωt0+2πΩ/ω).由于Ω/ω≪1,因此WA≈WB,也就是说,在固有频率的任一周期内,激励项w的变化非常小,虽然从更长的时间来看,w会在−A和+A之间变化.整个外激励项w可以视为一个慢变参数.下面我们分析系统((1)式)随慢变参数w变化的分岔行为.

系统((1)式)的平衡点E±可以表示为E±(x0,y0,z0,u0)=(x0,0,±1−x0,∓1),其中x0满足f(x0)+w−x0=0,其相应的特征方程可以表示为

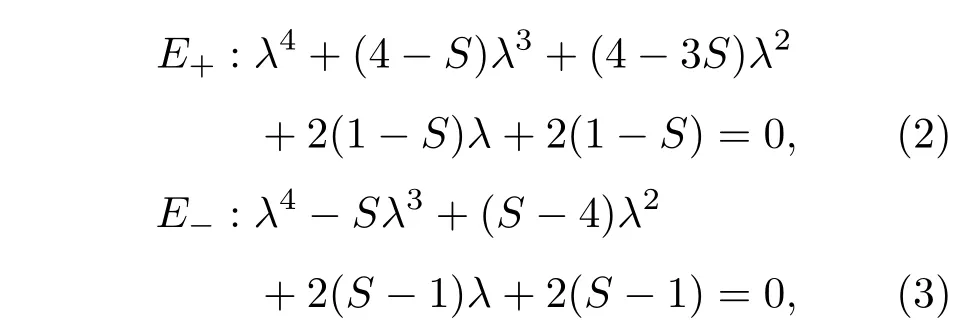
图1所示为β=2.0时系统随慢变参数w变化的平衡曲线,其中粗线表示稳定的平衡曲线,细线表示不稳定平衡曲线.从图1可以看出,随着w的变化,系统平衡点的数目在一、三和五之间变化.

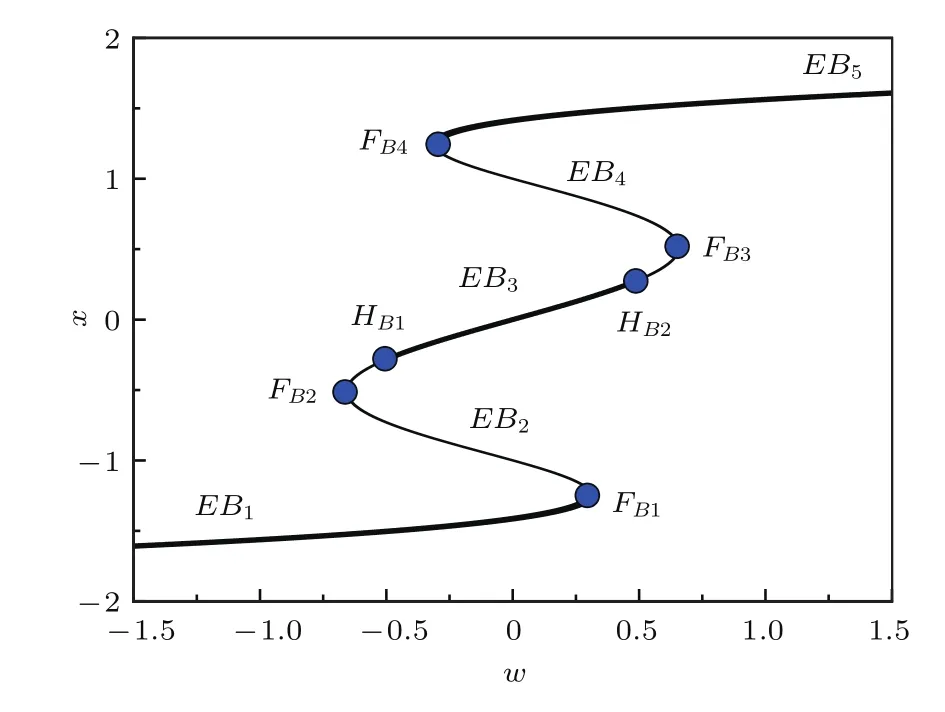
图1 系统随慢变参数w变化的平衡曲线及分岔点图Fig.1.Equilibrium branches as well as bifurcation points with the variation of the slowly-varying parameter w.

当w=0.3083时,稳定平衡曲线EB1与不稳定平衡曲线EB2在Fold分岔点FB1相遇,平衡线EB3由两Hopf分岔点HB1和HB2(w=±0.4626)分为三段,两分岔点HB1和HB2之间为稳定焦点,其他两段为不稳定鞍点,分别与不稳定平衡曲线EB2和EB4在Fold分岔点FB2(w=−0.6569)和FB3(w=0.6569)相遇.不稳定平衡曲线EB4和稳定平衡曲线EB5在Fold分岔点FB4(w=−0.3083)相遇.

4 周期簇发振荡

由于存在频域上的不同尺度,系统会产生一些特殊的振荡形式.从图1可以发现,当A<0.3083时,平衡曲线不含有分岔点,数值模拟发现,此时系统轨迹表现为周期振荡,其振荡频率为外激励频率,不存在快慢两尺度相互作用导致的簇发振荡.当A>0.3083时,系统会出现复杂的簇发振荡行为.为考察系统的不同尺度效应,本文分析三种典型情形,即A=0.6,3.0,6.0时系统的复杂动力学特性.

4.1 情形一:A=0.6

图2所示为A=0.6时系统的周期振荡相图.从图1可以看出,当A=0.6,即w∈[−0.6,0.6]时,快子系统最多可存在三个稳定的平衡点,分别位于平衡曲线EB1,EB3和EB5上,系统轨迹则围绕这三个稳定的平衡点振荡(图2).结合图3中x的时间历程可以发现,由于慢变量w变化非常缓慢,轨迹沿稳定的平衡曲线EB5运动到快子系统的Fold分岔点FB4时,产生跳跃现象,使得轨迹趋向稳定平衡曲线EB3.

图2 A=0.6时的相图(a)x-y平面上的相图;(b)z-u平面上的相图Fig.2.Phase portrait for A=0.6:(a)Phase portrait on the x-y plane;(b)phase portrait on the z-u plane.

分岔点FB4与w=−0.3083所对应的位于EB3上的快子系统平衡点之间距离较大,导致轨迹发生大幅振荡,随着慢变量w的继续减小,振荡幅值逐渐减小,轨迹逐渐稳定于EB3,并沿平衡曲线EB3继续运动.当轨迹抵达Hopf分岔点HB1时,产生围绕EB3的振荡,振荡幅值随w的继续减小而逐渐增加.当振荡幅值增大到一定值时,轨迹转向围绕EB1振荡,并逐渐稳定到EB1上.

为进一步揭示该周期簇发振荡的分岔机理,图4分别给出了w-x平面上的相图及其与快子系统平衡曲线的叠加图.

假设轨迹从w的最小值w=−0.6,即A1点出发(图4(a)),由于受稳定的平衡曲线EB1的影响,此时轨迹几乎严格沿EB1运动,表现为沉寂态QS1.当轨迹运动到分岔点FB1附近时,由Fold分岔产生跳跃现象,导致大幅振荡,进入激发态SP1.随慢变参数w的增加,振荡幅值减小,并逐渐趋于稳定平衡曲线EB5,而后几乎严格沿EB5运动,进入沉寂态QS2.

图3 A=0.6时x的时间历程Fig.3.Time history of x for A=0.6.

当慢变量w到达其最大值w=0.6,即A3点处,w会随时间的推进而减小,使得轨迹在A3点调头,几乎严格沿EB5运动,直到抵达分岔点FB4附近,由Fold分岔产生跳跃现象,导致大幅振荡,进入围绕稳定平衡曲线EB3振荡的激发态SP2.随着慢变量w的减小,振荡幅值减小,并逐渐稳定于平衡曲线EB3,进入沉寂态QS3.

当轨迹沿EB3运动到分岔点HB1时,由Hopf分岔产生围绕EB3的振荡,随着w的减小振荡幅值逐渐增加,进入激发态SP3.图5所示为从激发态SP3回到沉寂态QS1的分岔机理.

图4 (网刊彩色)(a)A=0.6时w-x平面上的转换相图;(b)A=0.6时w-x平面上快子系统平衡曲线与转换相图的叠加图Fig.4.(color online)(a)Transformed phase portrait on the w-x plane when A=0.6;(b)overlap of equilibrium orbit and transformed phase portrait on the w-x plane when A=0.6.

图5 (网刊彩色)激发态SP3到沉寂态QS1的分岔机理Fig.5.(color online)Bifurcation mechanism of the spiking state SP3to the quiescent state QS1.

当轨迹处于大幅振荡的激发态SP3时,随着w减小,激发态振荡幅值逐渐增加,当振荡幅值增加到一定程度时,与位于EB2上的不稳定鞍点相互作用,产生Saddle on limit cycle分岔,导致从Hopf分岔点HB1分岔出的极限环失稳,轨迹产生跳跃现象,为快子系统稳定的平衡曲线EB1吸引,进入沉寂态QS1,并几乎严格沿EB1运动,随后抵达慢变量w的极小值w=−0.60,即回到出发点A1,完成一个周期的簇发振荡.根据沉寂态和激发态相互转化的分岔模式可以将其称为非对称Fold/Fold-Hopf型簇发.

4.2 情形二:A=3.0

随着激励幅值的增加,簇发振荡吸引子的结构也会发生变化.图6所示为A=3.0时簇发振荡分别在x-y和z-u平面上的相图,从图中可以看出,与A=0.6时的相图不同,轨迹不会收敛到快子系统的稳定平衡曲线EB3上,而是围绕该平衡曲线产生大幅振荡.

从图7的时间历程可以发现,轨迹几乎严格按照平衡曲线EB1运动,由Fold分岔跳跃到稳定平衡曲线EB5上,又由Fold分岔,产生跳跃现象,轨迹转向围绕稳定平衡曲线EB3振荡.当轨迹尚未收敛到稳定曲线EB3上时,由于产生Hopf分岔,轨迹发生围绕该平衡曲线的振荡,且振荡幅值随着时间的推进逐渐增加,轨迹由Saddle on limit cycle分岔跳向稳定平衡曲线EB1.

图8(a)所示为A=3.0时系统轨迹的转换相图与快子系统平衡曲线的叠加图,图8(b)为其局部放大图.

假设轨迹从慢变量w的最小值w=−3.0,即A1点出发,从图8(a)可以看出,轨迹几乎严格沿稳定平衡曲线EB1运动,处于沉寂态QS1.当轨迹抵达分岔点FB1时,由Fold分岔产生跳跃现象,轨迹跳向稳定平衡曲线EB5,由于Fold分岔点与平衡曲线EB5之间的距离较大,产生大幅振荡,进入激发态SP1(图8(b)).随着w的增加,轨迹逐渐稳定到平衡曲线EB5,并几乎严格沿EB5运动,进入沉寂态QS2,直到抵达慢变量w的最大值w=3.0,即A3点.

图6 A=3.0时的相图(a)x-y平面上的相图;(b)z-u平面上的相图Fig.6.Phase portrait for A=3.0:(a)Phase portrait on the x-y plane;(b)phase portrait on the z-u plane.

图7 A=3.0时x的时间历程Fig.7.Time history of x for A=3.0.

图8 (网刊彩色)A=3.0时w-x平面上(a)快子系统平衡曲线与转换相图的叠加图及(b)其局部放大图Fig.8.(color online)(a)Overlap of equilibrium orbit and transformed phase portrait on the w-x plane and(b)locally enlarged diagram of the overlap when A=3.0.

随着时间的继续增加,慢变量w减小,导致轨迹在A3点调头,并几乎严格沿稳定平衡曲线EB5运动,依然处于沉寂态QS2,直到抵达分岔点FB4,由Fold分岔产生跳跃现象,导致轨迹转向稳定平衡曲线EB3,产生大幅振荡,进入激发态SP2.随着w的减小,振荡幅值逐渐减小,直到抵达分岔点HB1,由Hopf分岔,导致振荡幅值随w的减小而增加.

当振荡幅值增加到一定程度时,轨迹由Saddle on limit cycle分岔跳向稳定平衡曲线EB1,并随慢变量w的继续减小而逐渐稳定到稳定平衡曲线EB1上,进入沉寂态QS1,直到轨迹回到出发点A1,完成一个周期的振荡.

必须指出的是,该簇发振荡与图4中簇发振荡结构大致相似,最大区别在于围绕平衡曲线EB3附近的轨迹结构.由快子系统在分岔点FB4时的慢变量值w=−0.3083可知,此时在平衡曲线EB3上的x值为x0=−0.1632,其相应的特征值可以计算为λ1=−2.2683,λ2=−3.3063,λ3,4=−0.0946±0.8533I,表明该快子系统平衡点为稳定焦点.

在稳定平衡线EB3失稳的Hopf分岔点xH=−0.2678处,相应快子系统平衡点的特征值分别为λ1=−2.7221,λ2=−1.5807,λ3,4=±0.7882I.从图9可以看出,此时激发态SP2振荡频率随时间变化而变化,当轨迹从沉寂态QS2进入激发态时,振荡频率的理论值大致接近在平衡曲线EB3相应平衡点处的一对共轭特征值的虚部,即ΩL2≈2π/0.8533=7.3634,这与图9中的数值结果ΩP2=2π/T2≈7.3713符合良好.当轨迹经过Hopf分岔点时,其振荡频率的理论值ΩL1≈2π/0.7882=7.9716,也与数值模拟结果ΩP1=2π/T1≈7.9654大致符合.

为进一步说明导致上述两周期簇发振荡在快子系统稳定平衡曲线EB3附近出现结构差别的原因,图10分别给出了两激励幅值下系统及慢变量w随时间变化的历程.由上述分析可知,当慢变量w=−0.3083时,轨迹产生Fold分岔,而在w=−0.4626时,则产生Hopf分岔.从图10(b)可以看出,当A=0.6时,慢变量w分别到达两分岔点的时间间隔T2=317.68,而当A=3.0时,时间间隔T1=51.83,这与图10(a)中两真实轨迹之间时间上的距离TS1=313.54及TS2=53.16均符合良好.

图9 A=3.0时x的时间历程局部放大图Fig.9.Locally enlarged time history of x for A=3.0.

从图10可以发现,虽然快子系统的平衡曲线及其相应的分岔点位置与外激励幅值无关,但是,随着外激励振幅的增加,轨迹从沉寂态QS2由Fold分岔进入激发态,抵达Hopf分岔点所需时间会越来越短.当A=0.6时,由于慢变量抵达Hopf分岔点需要较长的时间,因而随着时间的增加,从QS2由Fold分岔导致的激发态的振荡越来越小,能够逐渐稳定到快子系统的稳定平衡曲线EB3上.当外激励幅值较大,如A=3.0时,由于慢变量抵达Hopf分岔点的时间非常短,轨迹虽然受稳定平衡曲线EB3的吸引,但尚未收敛到该平衡曲线,就又发生Hopf分岔,使得振荡幅值随慢变量的减小而逐渐增加,图4中QS3消失,SP2和SP3合并为一个激发态,即图9中的SP2.

4.3 情形三:A=6.0

随着外激励幅值的继续增加,簇发振荡的吸引子结构还会发生变化.图11所示为A=6.0时簇发振荡分别在x-y和z-u平面上的相图,从图中可以看出,吸引子结构与前两种情形不同,主要是轨迹围绕稳定平衡曲线EB3部分的结构消失,从而表现为分别围绕稳定平衡曲线EB1和EB5振荡的点-点型簇发振荡.

图12为状态变量x的时间历程,从图中可以看出,几乎严格沿稳定平衡曲线EB1运动的轨迹,由Fold分岔产生跳跃现象,导致轨迹趋向稳定平衡曲线EB5,当轨迹逐渐稳定于EB5后,便几乎严格沿该平衡曲线运动,直到再次发生Fold分岔,跳向稳定平衡曲线EB1.

通过图12中时间历程的计算可以发现,由稳定平衡曲线EB1跳向EB5产生振荡的频率ΩM1=2π/T1=0.8791,由EB5跳向EB1产生振荡的频率ΩM2=2π/T2=0.8763,分别近似于快子系统位于稳定平衡曲线EB5和EB1上与该跳跃点对应的平衡点的特征值一对共轭复根的虚部,也就是说,两振荡过程分别近似等于从不同跳跃点出发向各种稳定平衡曲线逐渐逼近的过程.

图11 A=6.0时的相图(a)x-y平面上的相图;(b)z-u平面上的相图Fig.11.Phase portrait for A=6.0:(a)Phase portrait on the x-y plane;(b)phase portrait on the z-u plane.

为进一步揭示该周期簇发振荡的产生机理,图13(a)给出了A=6.0时系统轨迹的转换相图与快子系统平衡曲线的叠加图,图13(b)为其局部放大图.

假设轨迹从慢变量w的最小值w=−6.0,即图13(a)中的A1点出发,轨迹几乎严格沿稳定平衡曲线EB1运动,表现为沉寂态QS1,直到轨迹抵达分岔点FB1,由Fold分岔跳向EB5,产生大幅振荡,进入激发态SP1,振荡幅值随慢变量w的增加而逐渐减小,直至收敛于稳定平衡曲线EB5,进入沉寂态QS2.

图12 A=6.0时x的时间历程Fig.12.Time history of x for A=6.0.

图13 (网刊彩色)A=6.0时(a)w-x平面上快子系统平衡曲线与转换相图的叠加图及(b)其局部放大图Fig.13.(color online)(a)Overlap of equilibrium orbit and transformed phase portrait on the w-x plane and(b)locally enlarged diagram of the overlap when A=6.0.

沿稳定平衡曲线EB5运动的轨迹在慢变量w达到其最大值w=6.0,即图13(a)中的A3点时,由于慢变量随时间的增加而减小,轨迹在A3点处调头,继续沿EB5运动,直到抵达分岔点FB4,由Fold分岔跳向EB1,产生大幅振荡,进入激发态SP2,振荡幅值随慢变量w的增加而逐渐减小,收敛于稳定平衡曲线EB1,进入沉寂态QS1,直至抵达出发点A1,完成一个周期的振荡.从簇发振荡分类的角度来看,该簇发振荡可以称为非对称点-点型Fold/Fold簇发.

必须指出的是,从分岔点FB1和FB4产生的Fold分岔均不趋向稳定平衡曲线EB3.产生这一现象的主要原因是,当外激励幅值较大时,系统能量的交换力度迅速增强,导致能量居中的稳定平衡曲线EB3的吸引域快速收缩,即分岔点FB1和FB4跳出了稳定平衡曲线EB3的吸引域,这也可以通过以分岔点为初值对快子系统进行的数值仿真得到证实.

5 结论

存在频域两尺度的动力系统在非对称控制器作用下会引发各种模式的非对称簇发振荡.当激励频率远小于系统的固有频率时,整个外激励项可以视为慢变参数.在考察系统随外激励幅值变化的动力学演化过程时,虽然快子系统存在一致的平衡曲线及相应的分岔图,但随着外激励幅值的变化,簇发振荡的结构及其产生机理存在差异.一方面,外激励幅值的变化会引起不同稳定平衡曲线吸引域的变化,另一方面,也会使得慢变量穿越不同分岔点的时间间隔发生变化,从而导致系统产生不同形式的簇发振荡.

[1]Cardin P T,de Moraes J R,da Silva P R 2015 J.Math.Anal.Appl.423 1166

[2]Hodgkin A L,Huxley A F 1990 Bull.Math.Biol.52 25

[3]Sánchez A D,G.Izús G,Erba M G,Deza R R 2014 Phys.Lett.A 378 1579

[4]Rakaric Z,Kovacic I 2016 Mech.Syst.Signal Process.81 35

[5]Chumakov G A,Chumakova N A 2003 Chem.Eng.J.91 151

[6]Jia F L,Xu W,Li H N,Hou L Q 2013 Acta Phys.Sin.62 100503(in Chinese)[贾飞蕾,徐伟,李恒年,侯黎强2013物理学报62 100503]

[7]Yang S C,Hong H P 2016 Eng.Struct.123 490

[8]Cai Z Q,Li X F,Zhou H 2015 Aerosp.Sci.Technol.42 384

[9]Li X H,Hou J Y 2016 Int.J.Non-Linear Mech.81 165

[10]Yu B S,Jin D P,Pang Z J 2014 Sci.Sin.Phys.Mech.Astron.44 858(in Chinese)[余本嵩,金栋平,庞兆君2014中国科学:物理学力学天文学44 858]

[11]Bi Q S 2012 Sci.China Ser.E10 2820

[12]Kim S,Lim W 2016 Neural Networks 79 53

[13]Izhikevich E M 2000 Int.J.Bifurcation Chaos 10 1171

[14]Izhikevich E M 2003 Trends Neurosci.26 161

[15]Shimizu K,Saito Y,Sekikawa M,Inaba N 2012 Physica D 241 1518

[16]Shilnikov A,Kolomiets M 2008 Int.J.Bifurcation Chaos 18 2141

[17]Han X J,Xia F B,Ji P,Bi Q S,Kurths J 2016 Commun.Nonlinear Sci.Numer.Si.36 517

[18]Bi Q S,Zhang R,Zhang Z D 2014 Appl.Math.Comput.243 482

[19]Yu Y,Zhang Z D,Bi Q S,Gao Y 2016 Appl.Math.Model 40 1816

[20]Zhang X F,Wu L,Bi Q S 2016 Chin.Phys.B 25 070501

[21]Xing Y Q,Chen X K,Zhang Z D,Bi Q S 2016 Acta Phys.Sin.65 090501(in Chinese)[邢雅清,陈小可,张正娣,毕勤胜2016物理学报65 090501]

[22]Zheng S,Han X J,Bi Q S 2011 Commun.Nonlinear Sci.Numer.Si.16 1998

[23]Vo T,Kramer M A,Kaper T J 2016 Phys.Rev.Lett.117 268101

[24]Zvonko R,Ivana K 2016 Mech.Syst.Signal Process.81 35

[25]Milicevic K,Nyarko E K,Biondic I 2016 Nonlinear Dyn.81 51

[26]Srinivasan K,Chandrasekar V K,Pradeep R G 2016 Commun.Nonlinear Sci.Numer.Si.39 156

PACS:05.45.–a,05.45.PqDOI:10.7498/aps.66.110501

Structures of the asymmetrical bursting oscillation attractors and their bifurcation mechanisms∗

Wu Tian-Yi1)2)Chen Xiao-Ke1)Zhang Zheng-Di3)Zhang Xiao-Fang1)Bi Qin-Sheng1)†
1)(Faculty of Civil Engineering and Mechanics,Jiangsu University,Zhenjiang 212013,China)
2)(Zhenjiang Watercraft College,Zhenjiang 212003,China)
3)(Faculty of Science,Jiangsu University,Zhenjiang 212013,China)

9 December 2016;revised manuscript

16 January 2017)

The main purpose of this study is to investigate the characteristics as well as the bifurcation mechanisms of the bursting oscillations in the asymmetrical dynamical system with two scales in the frequency domain.Since the slow-fast Hodgkin-Huxley model was established to successfully reproduce the activities of neuron,the complicated dynamics of the system with multiple time scales has become a hot research topic due to the wide engineering background.The dynamical system with multiple scales often presents periodic oscillations coupled by large-amplitude oscillations at spiking states and small-amplitude oscillations at quiescent states,which are connected by bifurcations.Up to now,most of the reports concentrate on bursting oscillations in the symmetric systems,in which there exists only one form of spiking oscillations and quiescence,respectively.Here we explore some typical forms of bursting behavior in an asymmetrical dynamical system with periodic excitation,in which there exists an order gap between the exciting frequency and the natural frequency.As an example,based on the typical Chua’s oscillator,by introducing an asymmetrical controller and a periodically changed current source,and choosing suitable parameter values,we establish an asymmetrical dynamical system with two scales in the frequency domain.Since the exciting frequency is much smaller than the natural frequency,the whole periodic exciting term can be regarded as a slowly-varying parameter,leading to the fast subsystem in autonomous form.Since all the equilibrium curves and relevant bifurcations are presented in the form related to the slowly-varying parameter,the transformed phase portraits describing the evolution relationship between the state variables and the slowly-varying parameter are employed to account for the mechanism of the bursting oscillations.With the variation of the slowly-varying parameter,di ff erent equilibrium states and relevant bifurcations in the fast subsystem are presented.It is found that for di ff erent parameter values,multiple balance curves of the fast subsystem may coexist,which a ff ect the structure of the bursting attractor.For the other parameters fi xed to certain values,the balance curve with the variation of the slowly-varying parameter is presented.Three typical cases with di ff erent exciting amplitudes are considered,corresponding to di ff erent situations of coexistence of equilibrium states in the fast subsystem.In the fi rst case,there exist at most three stable equilibrium points in the fast subsystem.Bursting attractor that oscillates around the three points can be observed,in which fold and Hopf bifurcations lead to the alternations between spiking states and quiescent states,while in the second case,saddle on the limit cycle bifurcation may cause the repetitive spiking oscillations to jump to the equilibrium curve.In the third case with relatively large exciting amplitude,only two equilibrium curves may involve the bursting oscillations,in which fold bifurcations lead to the alternation between the quiescent states and spiking states.Unlike the structures of bursting oscillations in the symmetric system,di ff erentforms of asymmetrical bursting oscillations with di ff erent periodic exciting amplitudes can be observed,the mechanisms of which are presented.It is pointed out that the change of the external exciting amplitude,does not only cause the variation of the attracting basins corresponding to di ff erent stable equilibrium branches,but also leads to the change of the temporal intervals when the trajectory passes di ff erent bifurcation points,respectively,which results in di ff erent patterns of bursting oscillations.Furthermore,since the slowly-varying parameter determined by the whole exciting term changes between two extreme values determined by the amplitude,the trajectory of the bursting oscillations of the transformed phase portrait returns at the two extreme values.The properties of equilibrium branches between the two extreme values determine the forms of the moving attractors.

asymmetrical system,bursting oscillation,bifurcation mechanism,attractor structure

10.7498/aps.66.110501

∗国家自然科学基金(批准号:11472115,11472116)和国家自然科学基金重点项目(批准号:11632008)资助的课题.

†通信作者.E-mail:qbi@ujs.edu.cn

©2017中国物理学会Chinese Physical Society

http://wulixb.iphy.ac.cn

*Project supported by the National Natural Science Foundation of China(Grant Nos.11472115,11472116)and the Major National Natural Science Foundation of China(Grant No.11632008).

†Corresponding author.E-mail:qbi@ujs.edu.cn