基于最优化线性波数光谱仪的谱域光学相干层析成像系统∗
2018-06-14吴彤孙帅帅王绪晖王吉明赫崇君顾晓蓉刘友文
吴彤 孙帅帅 王绪晖 王吉明 赫崇君 顾晓蓉 刘友文
(南京航空航天大学理学院应用物理系,南京 210016)
1 引 言
光学相干层析成像技术(optical coherence tomography,OCT)是一种高速、高分辨率、非接触的生物医学光学成像技术[1−8],能够实现微米级分辨率和毫米级深度成像.该技术已经广泛用于生物医学研究、临床诊断和材料特性的无损检测等领域[9−15].在谱域OCT(spectral domain OCT,SDOCT)中,干涉光谱信号被光栅光谱仪探测[16].传统的光栅光谱仪由衍射光栅、聚焦透镜、线阵相机组成.根据光栅方程,光栅衍射角的正弦值与光波长呈线性关系,与光波数呈非线性关系,则光波数在线阵相机上呈非线性分布.传统光栅光谱仪的非均匀波数分布特性对谱域OCT成像产生两个影响:第一,直接对非线性波数光谱干涉信号进行傅里叶变换会导致轴向点扩散函数加宽;第二,线阵相机上每个像素所探测的带宽不相同会导致灵敏度随着成像深度增加而下降得很快[17].
为了解决非均匀波数分布问题,传统的做法是在傅里叶转换前对采集到的干涉光谱数据进行数值重采样,把在波长空间均匀分布的数据转换成波数空间均匀分布的数据[18].但是重采样过程计算量大,灵敏度下降仍然不能得到改善.另一种做法是基于线性波数光谱仪在不需要大计算量插值处理的基础上改善灵敏度下降性能.Hu和Rollins[19]第一次把线性波数光谱仪引进谱域OCT系统中,在衍射光栅和聚焦透镜之间插入一个BK7玻璃材质的等腰色散棱镜,以棱镜出射角对波数的导数来衡量波数线性度.在它们的设计中只考虑了棱镜顶角这一光学结构参数.Gelikonov等[20]设计的线性波数光谱仪同时考虑了棱镜顶角、棱镜入射面与光栅平面之间的夹角两个结构参数,并提出以波数相对偏差为准则评估波数线性度.Watanabe和Itagaki[21]优化了棱镜材料和光栅棱镜之间的夹角,以位置-波数导数的标准差作为线性波数优化准则.Lee等[22]通过数值模拟优化光学参数以实现超高分辨率成像,这些参数包括光栅的光栅常数、色散棱镜的材料、光栅和色散棱镜间的旋转角,其最优化角度和棱镜材料通过最小化角度-波数导数获得.最近,Lan和Li[23]设计的线性波数光谱仪用在谱域OCT系统中实现了超高分辨率成像,利用定量光线追迹技术计算了11个离散波数的均方根偏差,并以其为准则评估线性波数光谱仪中波数的线性度.
本文提出一个新的优化准则来优化线性波数光谱仪的结构参数,包括棱镜顶角、棱镜材料和光栅与棱镜之间的旋转角.把考虑的结构参数整合到波数和像素位置的理论关系式中以数值模拟光谱干涉信号及其点扩散函数,以点扩散函数半峰全宽值的倒数作为评价因子来优化这些结构参数.按照优化的结构参数搭建了线性波数光谱仪,实验测量了轴向分辨率和系统灵敏度,并与理论值比较以评估搭建的线性波数光谱仪的性能.最后用基于搭建的线性波数光谱仪的谱域OCT系统对人的手指指甲进行了在体层析成像.
2 方 法
线性波数光谱仪的结构示意图见图1,由准直镜、衍射光栅、色散棱镜、聚焦透镜和线阵相机组成.定义线性波数光谱仪的结构参数为:色散棱镜顶角α、棱镜入射面与光栅面之间的旋转角β、棱镜材料折射率n.为了使宽带光源带宽范围内的波数均匀分布在线阵相机像素上,需要推导像素位置坐标和波数之间的函数关系.如图1所示,令像素阵列的一端为坐标原点,中心像素位置坐标为x0,任一像素位置坐标为x.设计中首先应使宽带光源发出的中心波数激光聚焦在中心像素位置上.当满足闪耀条件时,中心波数激光的光栅衍射角θd0可以表示为
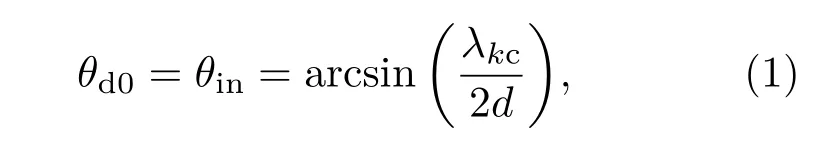
其中,λkc为中心波数对应的波长,d为光栅常数,θin为衍射光栅的入射角.如图1所示,定义棱镜出射角为棱镜右端面的出射光与法线的夹角.则中心波数的棱镜出射角θ0可以表示为

通过光线追迹,对应线阵相机上某个特定像素位置坐标x的棱镜出射角θout可以表示为
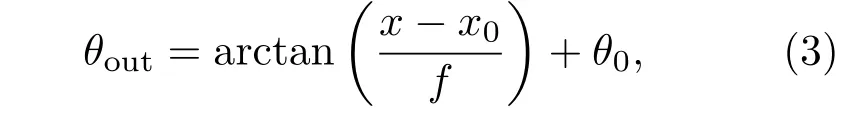
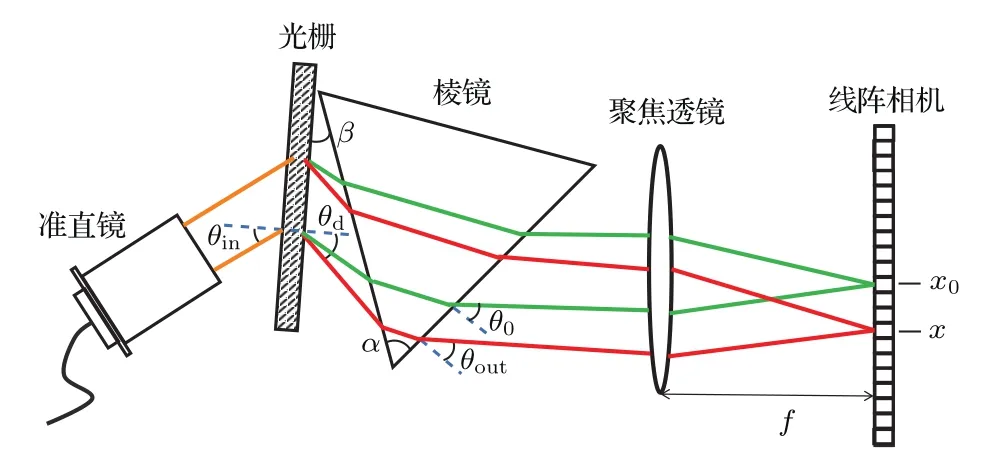
图1 线性波数光谱仪的结构示意图Fig.1.Schematics of the linear-k spectrometer.
其中f是聚焦透镜的焦距.给定一组线性波数光谱仪的结构参数(α,β,n),某波数对应的光栅衍射角θd可以由相应的棱镜出射角θout推出:

把(1),(3),(4)式代入光栅方程,可以得到像素位置坐标x和波数k之间的函数关系:
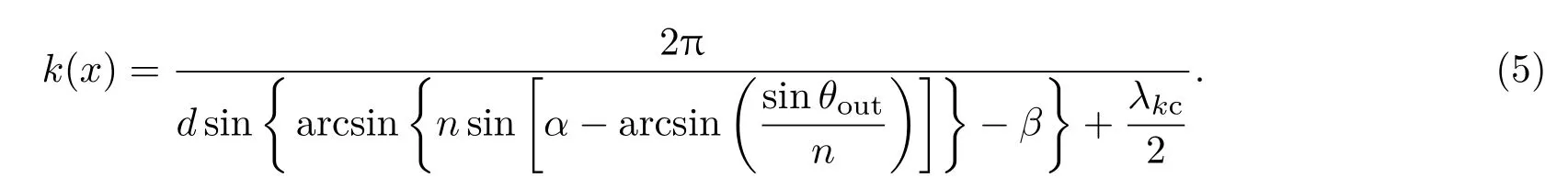
根据(5)式,可以数值模拟对应某组线性波数光谱仪结构参数的波数分布函数k(x),进而模拟对应样品某深度的干涉光谱信号2(k),表达式如下:
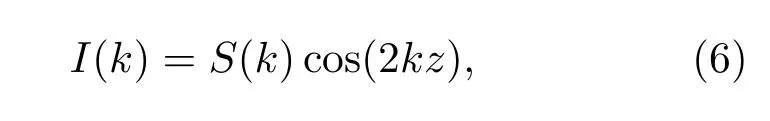
其中z代表样品深度位置坐标,k代表对应某组结构参数的波数分布函数,S(k)代表光源的光谱密度函数,理想情况下OCT光源的光谱分布可取为高斯分布,即有S(k)=S0exp(−(k−kc)2/∆k2),kc为光源的中心波数,∆k为光源的波数带宽.由干涉光谱信号的傅里叶变换可以得到对应于该样品深度的点扩散函数.点扩散函数即OCT成像系统的轴向分辨率.定义点扩散函数的半峰全宽(FWHM)值的倒数1/FWHM作为优化设计线性波数光谱仪结构参数的评价因子c.通过精细改变结构参数得到最高的c值即对应于优化的线性波数光谱仪设计.
可以通过计算相对偏差函数ε(x)评估优化线性波数光谱仪的波数线性度.偏差函数描述特定的波数分布函数k(x)和理想的线性波数分布函数k1(x)的偏差[20].理想的线性波数分布函数定义如下:
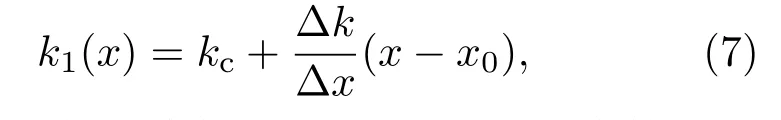
其中kc代表中心波数,∆x代表可探测波数范围∆k所对应的像素阵列空间范围.
相对偏差函数定义如下:
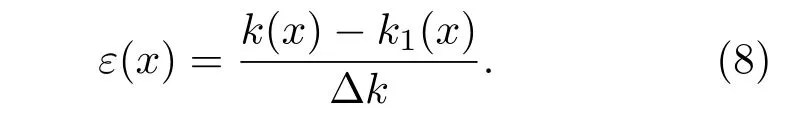
因此波数分布函数k(x)的非线性度可以用度量δε来数值估计,其表达式如下:
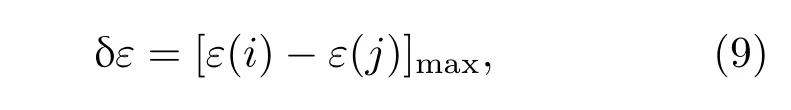
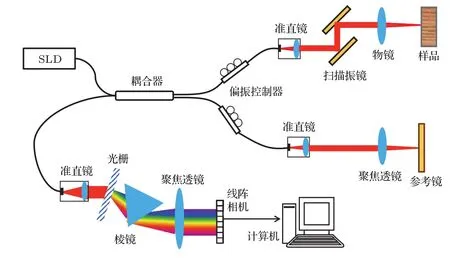
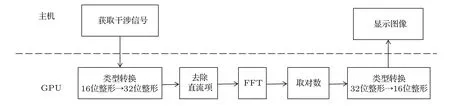
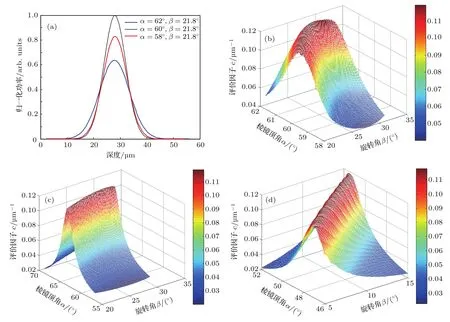
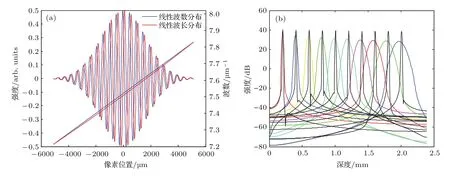
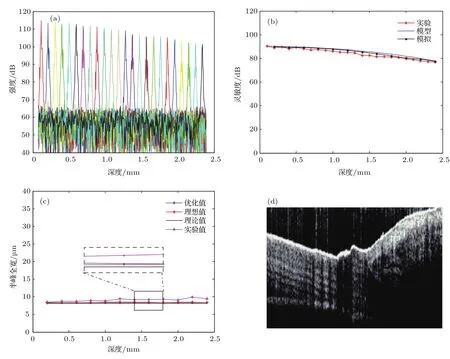
其中i和j代表像素序数(0 6i,j 优化线性波数光谱仪需要考虑的结构参数有棱镜顶角α、旋转角β和棱镜材料折射率n.在线性波数光谱仪的数值模拟优化中,首先根据商品化的光学元器件的典型参数指标设定模拟参数.其中透射式衍射光栅的光栅常数设定为1200线对每毫米,聚焦透镜焦距设定为100 mm,线阵扫描相机的单个像素尺寸设定为10µm,可探测的光谱带宽波数范围设定为7.189—7.854µm−1.色散棱镜的材料设定为F2,BK7和SF11,由于这三种光学玻璃材料在此可探测光谱范围内的折射率改变很小,模拟中材料折射率n设定为中心波数所对应的折射率.商品化的标准色散棱镜通常为等边棱镜,因此棱镜顶角的取值范围设定在60◦附近.旋转角的取值范围设定为21◦—31◦度.根据(5)和(6)式分别模拟波数分布函数以及对应的干涉光谱信号.深度z设置为典型值1.6 mm.经过对数值模拟的干涉光谱信号进行傅里叶变换可以计算对应的点扩散函数半峰全宽值及其评价因子c值.不同的α,β和n值可以取得不同的c值.一组使c值最大的α,β和n值即为优化的线性波数光谱仪结构参数.为了在理论上评价优化线性波数分布函数的非线性度,根据(7)和(8)式可得优化波数分布函数和理想线性波数分布函数之间的相对偏差函数ε(x),根据(9)式可得优化波数分布函数的非线性度δε. 图2是实验室搭建的谱域OCT系统结构示意图.光源为超发光二极管(SLD)宽带光源(SLD-371,Superlum公司),中心波长为840 nm,带宽为74 nm,最大输出功率约为11 mW.从光源发出的宽带激光经分光比为50/50的光纤耦合器分为两束后分别进入样品臂和参考臂.样品臂由偏振控制器、光纤准直镜、二维扫描振镜(GVS002,Thorlabs Inc.)、聚焦物镜和被测样品组成.参考臂由偏振控制器、光纤准直镜、聚焦透镜和平面反射镜(PF10-03-M03,Thorlabs Inc.)组成,其中偏振控制器用于调节参考臂的光波与样品臂的光波偏振方向一致.从参考镜和样品返回的光汇合后形成的干涉光谱条纹信号由优化的线性波数光谱仪探测.线性波数光谱仪由光纤准直镜、透射式衍射光栅、等边色散棱镜、聚焦透镜和一个线阵扫描互补金属氧化物半导体(CMOS)相机(sp2048-70 km,Basler Inc.)组成.为了校准和调节线性波数光谱仪中的光路,制作了光栅槽和棱镜槽用来固定光栅和棱镜,光栅槽与棱镜槽之间的夹角设定为优化的旋转角β.由线阵扫描CMOS相机探测到的干涉光谱条纹信号经图像采集卡(IMAQ PCIe-1430,National Instruments)采集进入计算机内存,经数据处理后得到OCT图像. 为了实现对干涉光谱信号的实时处理,搭建的谱域OCT成像系统使用支持通用并行计算性能的图形处理器GPU对采集到的谱域OCT干涉光谱信号进行处理.实时信号处理和图像显示流程如图3所示.首先,实时采集到的一帧干涉光谱信号数据从主机内存转移到GPU板载内存;干涉光谱信号数据在数据类型转换之后减除预先存储在GPU中的参考光强度;继而对一帧干涉光谱信号数据进行并行傅里叶变换(FFT)和对数变换,得到一帧OCT图像数据;再经过一次类型转换后OCT图像数据从GPU板载内存转移至计算机主机内存中,并在显示器显示OCT图像.包括干涉光谱信号采集、GPU并行处理以及OCT图像显示的图形用户界面使用基于Visual C++2008程序实现. 图2 基于最优化线性波数光谱仪的谱域OCT系统示意图Fig.2.Schematic of the SD-OCT system with the optimized linear-k spectrometer. 图3 谱域OCT实时干涉光谱信号处理和显示流程图Fig.3.Flowchart of the real-time signal processing and displaying for the SDOCT system. 图4为基于Matlab程序优化线性波数光谱仪的模拟结果.其中图4(a)为固定旋转角的情况下,改变棱镜顶角时数值模拟的点扩散函数曲线,从图中可知点扩散函数的FWHM随着棱镜顶角的变化而变化.图4(b)—(d)分别为对应三种典型光学材料的评价因子模拟结果.其中图4(b)为采用F2玻璃色散棱镜的评价因子c值的模拟结果,当棱镜顶角为61.4◦、光栅与棱镜间的旋转角为29.7◦时,评价因子c值达到最大值0.1190µm−1,其最优化棱镜顶角范围是59.6◦—61.8◦.图4(c)为采用BK7玻璃色散棱镜的评价因子模拟结果,当棱镜顶角为66.4◦、光栅与棱镜间的旋转角为27.1◦时,评价因子c值达到最大值0.1189µm−1,其最优化棱镜顶角范围是65.7◦—66.8◦.图4(d)为采用SF11玻璃色散棱镜的评价因子模拟结果,其材料特性和前两者差异较大,当棱镜顶角为51.4◦、光栅与棱镜间的旋转角为14.9◦时,评价因子c值达到最大值0.1181µm−1,其最优化棱镜顶角范围是49.5◦—51.0◦.综合三种典型材料的数值模拟结果,在60◦附近F2棱镜的评价因子明显大于BK7棱镜相对应的评价因子,且F2棱镜的最优化角度范围比较大;而BK7和SF11棱镜情况下的评价因子对角度变化比较敏感.考虑到商品化的色散棱镜通常都为等边棱镜,根据数值模拟结果,实验中选择F2等边色散棱镜用于搭建线性波数光谱仪.由图4(b)可知当F2色散棱镜顶角角度为60◦时,光栅与棱镜间的最优化旋转角为21.8◦. 在最优化结构参数情况下,理论评估线性波数光谱仪波数线性度的结果如图5所示.当深度坐标z取0.2 mm,线阵相机上探测的光谱信号分别为波长线性分布和波数线性分布情况下,波数与像素位置关系曲线以及根据(5)式模拟的干涉光谱信号如图5(a)所示,红色曲线表示波长呈线性分布时的波数-像素关系曲线及对应的干涉光谱信号,蓝色曲线表示波数呈线性分布时的波数-像素关系曲线及对应的干涉光谱信号.图5(b)所示为模拟的基于两种光谱仪即线性波长光谱仪和线性波数光谱仪的谱域OCT系统在不同成像深度处的点扩散函数对比图.如图所示,在较浅成像深度处,非线性波数分布对轴向分辨率的影响不大,但随着成像深度的增加,非线性波数情况下的点扩散函数显著加宽.根据(8)式可以计算优化的波数分布函数和理想的波数分布函数之间的相对偏差函数ε(x).根据计算结果δε=0.045%低于临界值1/N=0.1%,表明优化的线性波数光谱仪的波数线性度表现良好. 图4 (a)不同角度组合下的点扩散函数模拟图;F2棱镜(b),BK7棱镜(c)以及SF11棱镜(d)情况下评价因子数值模拟三维轮廓图Fig.4.(a)The simulated PSF under different combinations of angles;3D numerical simulation results of the cost factor for F2(b),BK7(c)and SF11(d)prism. 图5 (a)深度坐标为0.2 mm处的干涉光谱信号的模拟结果和波数线性度模拟结果,红色曲线对应于线性波长分布,蓝色曲线对应于线性波数分布;(b)线性波长干涉信号与线性波数干涉信号经FFT后的点扩散函数图像,彩色曲线对应线性波长情况,黑色曲线对应线性波数情况Fig.5.(a)Comparison of the simulated spectral interference signal at the depth coordinate of 0.2 mm(red,linearin-wavenumber case;blue,linear-in-wavelength case);(b)point spread functions directly Fourier transformed from the linear-in-wavelength signal(color curves)and linear-in-wavenumber signal(black curves). 为了通过实验评估搭建的线性波数光谱仪的性能,在谱域OCT系统中以平面反射镜作为样品采集并处理了几组干涉光谱信号.在进行直流项处理和FFT后,可以测得系统灵敏度、灵敏度下降曲线以及轴向分辨率.这些实验结果显示在图6中.从图6(a)可以看出,基于谱域OCT线性波数光谱仪的灵敏度在零光程附近处约为91 dB.在深度范围1.2 mm内,灵敏度下降低于6 dB. 图6 (a)基于谱域OCT系统的线性波数光谱仪灵敏度;(b)三种灵敏度下降曲线对比;(c)轴向分辨率的对比;(d)手指皮肤与指甲接缝处横断面OCT图像Fig.6.(a)The sensitivity of linear-k spectrometer based SDOCT system;(b)sensitivity roll-of fcomparison;(c)the comparison of axial resolution;(d)cross-sectional OCT images of human finger skin obtained by the constructed linear-k spectrometer based SDOCT system. 为了把灵敏度下降的实验结果和理论模型、模拟结果相比较,引用文献[17]提出的谱域干涉光谱信号解析模型.此解析模型可以表达如下: 其中A是干涉光谱信号强度,p是像素尺寸,R是线色散率,即光谱聚焦平面上1µm长度所占的光谱带宽,a是光谱聚焦光斑大小,z是成像深度.灵敏度下降对比曲线如图6(b)所示,其中红线代表实验测得的系统灵敏度下降曲线,蓝线代表在相机上光斑尺寸为6.8µm时用解析模型计算的理论灵敏度下降曲线,黑线代表数值模拟情况下最优化线性波数光谱仪灵敏度下降曲线,由代入最优化结构参数的波数函数求得.如图所示,实验测得的灵敏度下降性能和解析模型、数值模拟的结果基本一致.轴向分辨率的实验结果及其与理论值的对比如图6(c)所示.在图中,理论值是由OCT轴向分辨率公式δz=0.44λ2/∆λ决定的数值;优化值代表模拟点扩散函数的半峰全宽值;理想值代表在波数函数和像素位置成线性关系情况下模拟的点扩散函数的半峰全宽值;实验值代表用实验室搭建的基于线性波数光谱仪的谱域OCT系统测得的点扩散函数的半峰全宽值.在实验中,光源的半峰全宽为38 nm,理论轴向分辨率为8.14µm.当平面镜位于1.6 mm深度处,优化的轴向分辨率为8.45µm,等波数分布理想轴向分辨率为8.36µm,实验测得轴向分辨率9.15µm.由图中曲线可以看出,当深度较小时,实际轴向分辨率值接近于理论值;当深度较大时,两者存在一定差距,推测主要是由于线性波数光谱仪搭建误差引起.最后,对搭建的基于线性波数光谱仪的谱域OCT系统进行活体生物组织成像性能测试.图6(d)展示的是对人手指指甲皮肤接缝处组织进行成像的OCT图像结果,其横向和轴向视场范围分别为5.6 mm和2.4 mm.从图中可见,手指指甲组织、皮肤组织、指甲和皮肤接缝处组织结构清晰可见.高分辨率手指皮肤组织的活体成像结果证明了搭建的基于线性波数光谱仪的谱域OCT系统的成像性能. 提出了一个优化准则来优化线性波数光谱仪的结构参数.需要考虑的结构参数有棱镜材料、棱镜顶角和光栅与棱镜间的旋转角.根据优化结果,选取F2玻璃等边色散棱镜、以光栅-棱镜间旋转角角度为21.8◦搭建了最优化线性波数光谱仪,并引入谱域OCT成像系统.实验测得成像系统的成像深度达到了2.42 mm,轴向分辨率达到8.52µm,灵敏度达到91 dB,6 dB成像深度达到1.2 mm.该线性波数光谱仪大大改善了光谱线性度,并在不需要重新采样的情况下即能获得高分辨率OCT图像.利用GPU的并行运算能力实时显示了横断面OCT图像. [1]Huang D,Swanson E A,Lin C P,Schuman J S,Stinson W G,Chang W,Hee M R,Flotte T,Gregory K,Puliafito C A,Fujimoto J G 1991Science254 1178 [2]Fercher F A,Hitzenberger C K,Kamp G,Elzaiat S Y 1995Opt.Commun.117 43 [3]Hausler G,Lindner M W 1998J.Biomed.Opt.3 21 [4]Cho H S,Jang S J,Kim K,Dan A V,Shishkov M,Bouma B E,Oh W Y 2013Biomed.Opt.Express5 223 [5]Wang R K,Zhang A Q,Choi W J,Zhang Q Q,Chen C L,Miller A,Gregori G,Rosenfeld P J 2016Opt.Lett.41 2330 [6]Liang Y M,Zhou D C,Meng F Y,Wang M W 2007Acta Phys.Sin.56 3246(in Chinese)[梁艳梅,周大川,孟凡勇,王明伟2007物理学报56 3246] [7]Jia Y Q,Liang Y M,Zhu X N 2007Acta Phys.Sin.56 3861(in Chinese)[贾亚青,梁艳梅,朱晓农2007物理学报56 3861] [8]Huang L M,Ding Z H,Hong W,Wang C 2011Acta Phys.Sin.60 023401(in Chinese)[黄良敏,丁志华,洪威,王川2011物理学报60 023401] [9]Leitgeb R,Hitzenberger C K,Fercher A F 2003Opt.Expresss11 889 [10]Choma M A,Sarunic M V,Yang C,Izatt J A 2003Opt.Express11 2183 [11]Brauer B,Murdoch S G,Vanholsbeeck F 2016Opt.Lett.41 5732 [12]Zhang M,Hwang T S,Campbell J P,Bailey S T,Wilson J D,Huang D,Jia Y 2016Biomed.Opt.Express7 816 [13]Photiou C,Bousi E,Zouvani I,Pitris C 2017Biomed.Opt.Express8 2528 [14]Chen J B,Zeng Y G,Yuan Z L,Tang Z L 2018Acta Opt.Sin.38 0111001(in Chinese)[陈俊波,曾亚光,袁治灵,唐志列2018光学学报38 0111001] [15]Gao W R,Chen Y D,Liu C,Zhang T Q,Zhu Y 2016Acta Opt.Sin.45 0611001(in Chinese)[高万荣,陈一丹,刘畅,张秋庭,朱越2016光学学报45 0611001] [16]Bao W,Ding Z H,Wang C,Mei S T 2013Acta Phys.Sin.62 114202(in Chinese)[鲍文,丁志华,王川,梅胜涛2013物理学报62 114202] [17]Hu Z L,Pan Y S,Rollins A M 2007Appl.Opt.46 8499 [18]Dorrer C,Belabas N,Likforman J P,Jo ff re M 2000J.Opt.Soc.Am.B17 1795 [19]Hu Z L,Rollins A M 2007Phys.Opt.Lett.32 3525 [20]Gelikonov V M,Gelikonov G V,Shilyagin P A 2009Opt.Spectrosc.106 459 [21]Watanabe Y,Itagaki T 2009J.Biomed.Opt.14 48 [22]Lee S W,Kam H,Joo H P,Tae G L,Eun S L,Jae Y L 2015J.Opt.Soc.Korea19 55 [23]Lan G P,Li G Q 2017Sci.Rep.7 753 模拟与实验
4 结 果
4.1 模拟结果
4.2 实验结果
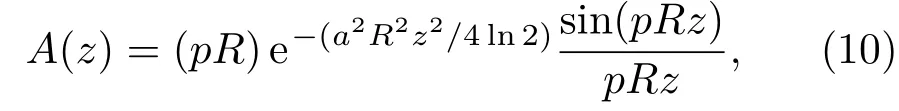
5 结 论
