黏性颗粒在鼓泡床中局部流动结构的数值模拟
2017-08-08罗传宝王梦迪牛全亮
罗传宝,周 涛,王梦迪,牛全亮
(中南大学 化学化工学院,湖南 长沙 410083)
黏性颗粒在鼓泡床中局部流动结构的数值模拟
罗传宝,周 涛,王梦迪,牛全亮
(中南大学 化学化工学院,湖南 长沙 410083)
因颗粒间的团聚效应,黏性颗粒在鼓泡床中流动特征比粗颗粒的更为复杂,呈现出颗粒、聚团、床层上的多尺度结构。因此,提出采用系统分解思路,将流动结构非均匀的黏性颗粒鼓泡床系统分解为乳化相、气泡相和相间相3个均匀的子系统,并引入7个结构参数描述该系统的局部流动结构。利用聚团的力平衡模型、气固两相的连续性方程、动量守恒方程及经验公式,构建该体系的局部结构参数模型。最后,以黏性氧化铝颗粒在鼓泡床中的流化作为算例,采用全局搜索算法求解结构参数以评价该模型的合理性。实验结果表明,所选用的结构参数能够正确地反映黏性颗粒在鼓泡床中局部流动结构,并与已有文献报道和实验现象相吻合。因此,可用这些结构参数计算气固相间曳力和模拟流场的流动特性。
流态化;黏性颗粒;数值模拟;局部结构参数模型
1 研究背景
气固鼓泡流化床因具优良传质传热性能及易于实现连续化操作等优点,被广泛应用于石油化工、冶金和制药等领域[1]。随着科学技术的发展,特别是微细、超细或纳米材料研究的深入,流态化研究的重点也从大颗粒转移到更细微颗粒,开发适用于微细、超细或纳米材料加工与反应的鼓泡流化床反应器势在必行。与粗颗粒流态化相比,黏性颗粒因颗粒间黏附力较大,易形成颗粒聚团结构[2-3]。这种以聚团形式的流态化呈现出颗粒、聚团、整体等多尺度的非均匀结构特征[4-5],加剧了系统的复杂性和非平衡性,阻碍了采用实验对其流化机制的进一步认知与探索。
21世纪初,随着计算机和软件技术的方兴未艾,计算流体力学因可展现颗粒流态化中最本质的流动细节而备受关注。目前,用于模拟鼓泡床的计算流体力学方法主要有颗粒轨道模型、直接数值模型和连续介质模型。其中,连续介质模型因计算量小,便于实现等优点而被广泛应用。连续介质模型将颗粒相假定为类似流体的连续相(拟流体),流场可视为两种流体各自流动,而两流体间通过相间曳力模型关联。因此,采用连续介质模型模拟的准确性主要依赖于所选择的曳力模型[6]。传统的曳力模型(如Symalal-O’Brien模型[7]等)多基于均匀流态化假设,或源于均匀的液固流态化系统或固定床实验数据。然而,均匀流态化的理想假设仅存在于散式流态化中,对于黏性颗粒鼓泡床等典型聚式流态化并不适用。因此,构建适用于复杂多尺度流动结构的曳力模型迫在眉睫。
近年来,流态化技术及颗粒领域学者一直致力曳力模型的研究和改进,并意识到介尺度层面上的颗粒团聚在曳力问题上扮演了极其重要的角色。其中的突破性进展之一是提出了采用多尺度最小能量理论(theory of energy minimization multi-scale, EMMS)构建非均匀结构曳力模型的理论方法。迄今为止,已发展成若干模型,简记为EMMS曳力模型[8-9]。但这些非均匀结构曳力模型的准确性却取决于可准确描述系统内部非均匀流动的结构参数。综上可知,结构参数在鼓泡床流场模拟中扮演着举足轻重的角色。
本文拟以黏性颗粒鼓泡流化床为研究对象,采用系统分解思路,将流动结构非均匀的总系统分解为若干均匀子系统,依据整体和各子系统间的质量守恒、动量守恒和所适用的经验公式及理论模型,构建更为恰当和精准的局部结构参数模型。并提出以全局搜索算法求解该模型,得出可描述局部流动的结构参数,根据实验研究规律评价其合理性,实现黏性颗粒鼓泡床结构曳力模型的建立和流场模拟,并为其它复杂气固多相流系统的数值模拟提供理论参考。
2 局部结构参数模型的构建
2.1 系统的分解
由图1所示系统分解思路,将具非均匀流动的黏性颗粒鼓泡床分解为均匀流动的乳化相、气泡相和相间相。通过系统分解,使原来仅适用于散式流态化的理论扩展到聚式流态化中的各子系统。采用7个结构参数描述黏性颗粒在鼓泡流化床中的局部流动结构:乳化相空隙率εe,颗粒团粒径da,乳化相中气体表观速率Uge,气泡整体运动速率Ub,气泡相体积分数fb,气泡中气体流动表观速率Ugb,气泡直径db。
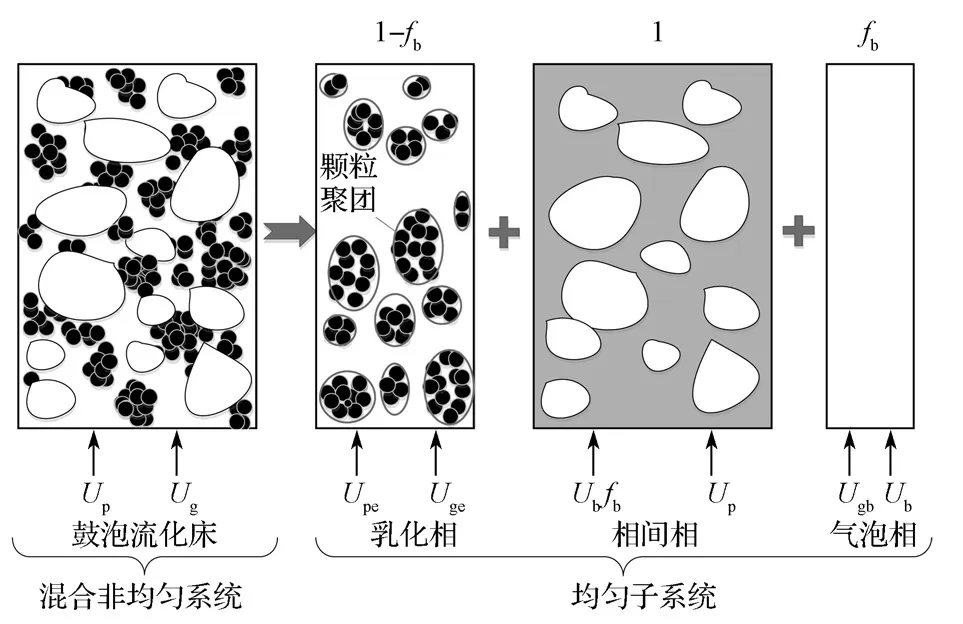
图1 黏性颗粒鼓泡床的系统分解Fig.1 System decomposition of the bubbling fl uidized bed operated with cohesive particles
对于鼓泡流化床,由于其并不具有颗粒循环,体系平均颗粒速率可近似为0。此外,不妨假设气泡只存在于气泡相中,则仅由颗粒团和空气组成的乳化相可被作为流体处理,其对应的密度ρe、黏度μe[10]和表观速率Ue可由式(1)~(3)确定。
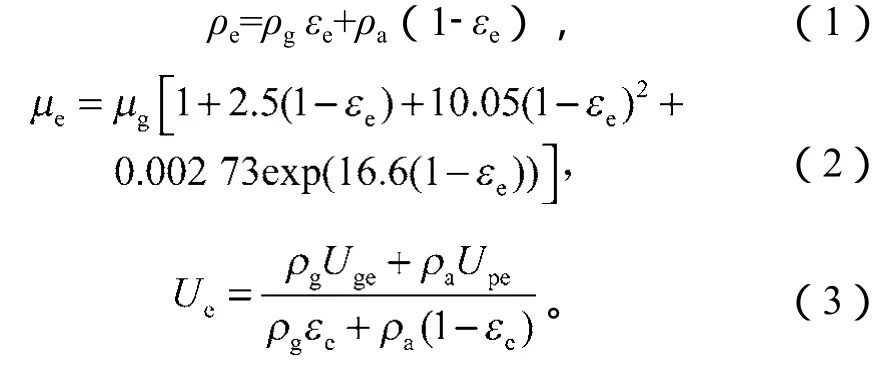
式(1)~(3)中:ρa,ρg分别为颗粒团和空气的密度;μg为空气的黏度;Upe,Uge分别为颗粒团和空气在乳化相中的表观速率。
2.2 模型的建立
以7个结构参数对床层非均匀流动结构进行描述的关键是构建并求解这些结构参数的独立方程,从而确定各结构参数的分布。这些结构参数中,颗粒团粒径居主导地位,其他结构参数均依赖其变化。
作为介尺度结构典型代表的颗粒团,其粒径影响着床层流动特征。流化中的颗粒团粒径也并非是一成不变的,而是存在着破碎与合并平衡。因此,聚团粒径随空间和时间的不同而呈现出差异。Zhou T.等综合分析了处于流化中的聚团所受的曳力、碰撞力、黏性力、重力和浮力,并依据受力平衡原理构建了可以确定聚团粒径的模型[11],且设计了大量实验对所提模型的准确性进行了验证。本研究采用该模型,其表达式为:
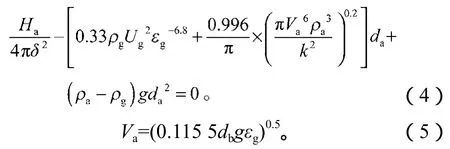
式(4)和(5)中:Ha为Hamaker常数;Ug为操作时的表观气速;δ为两颗粒聚团间的距离;k为杨氏模量与泊松比的函数,可根据实验测定其泊松比和弹性模量计算,对于黏性颗粒聚团流化床,若无实验测量值,其值可取3×10-6Pa-1[12];g为重力加速度;εg为局部平均空隙率,可由式(6)确定。

作为鼓泡床中另一主要相的气泡,其在床层内的运动规律也得到了学者们的青睐。适用于粗颗粒鼓泡床中气泡生长规律的Darton模型虽已被学者们大量研究和论证[13],但并不适用于流动更复杂的黏性颗粒鼓泡床体系。因此本研究选用Zou Z.等仅针对黏性颗粒鼓泡床中气泡变化特点而给出的经验公式[14],即:
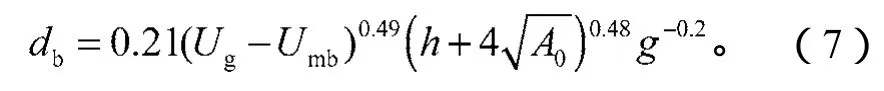
式中:Umb为最小鼓泡速率;h为局部床层高度;A0为气体分布板上的总空隙面积。
对于乳化相整体,此结构均匀的子系统可视为散式流态化,则流体对乳化相中颗粒团的曳力可用Ergun方程计算[15]。以单位乳化相体积作为衡算对象,其力学平衡方程可写为

式中:Usb为气泡与乳化相间表观滑移速率,可由式(11)确定,

最后,对于气泡中气体流动表观速率,当气泡表观流动速率小于气体在乳化相中的真实流动速率时,气体将穿过气泡并进入乳化相中,两者表观速率相等;反之,则表示气体仅追随着气泡运动,而并没有气体穿过气泡,即气泡中气体流动表观速率为0。根据上述分析,不难得出如下数学关系:
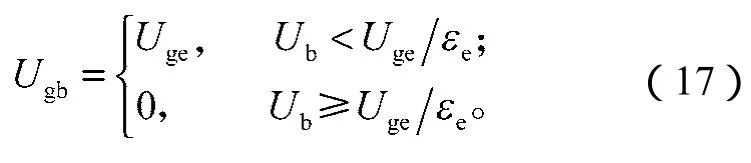
2.3 模型求解
以超细氧化铝颗粒的鼓泡流化作为算例,其物性参数及计算参数如表1所示。

表1 局部结构参数模型的迭代求解参数Table 1 Iterative solution of the local structural parameter model
所建立的局部结构参数模型只有7个独立方程,恰好能求解出7个结构参数,但上述方程多为非线性方程,且方程间耦合关系复杂,并不能通过解析求解。但是,有些结构参数的变化范围是可以确定的,比如乳化相空隙率εe的取值范围为0~1。因此,为保证局部结构参数的顺利求解,提出全局搜索算法,即在其全局范围内对床层高度h和乳化相空隙率εe遍历,逐步迭代求解,直至所有参数均满足上述方程。整个计算过程借助于Matlab软件,具体流程如图2所示。图中Usb,guess为气泡相与乳化相间表观滑移速率的假定值;da,guess为聚团粒径的假定值;ξ0为计算Usb的迭代精度,在此取0.001 m/s;ξ1为计算da的迭代精度,在此取1 μm。
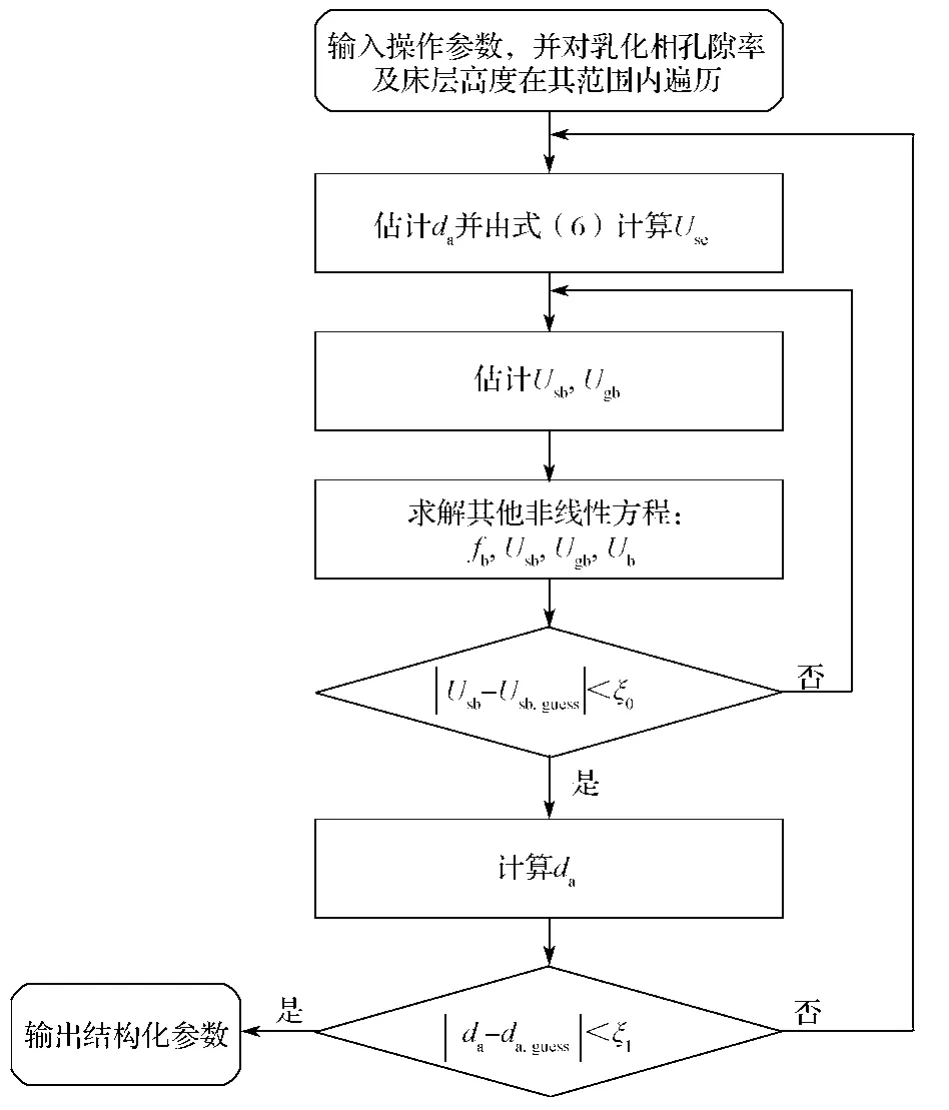
图2 全局搜索算法流程Fig. 2 A fl ow chart of the global search solution algorithm
3 局部结构模型的评价
3.1 气泡流动速率与床层高度和乳化相空隙率
图3给出了气泡流动速率随局部床层高度和乳化相空隙率的变化关系。
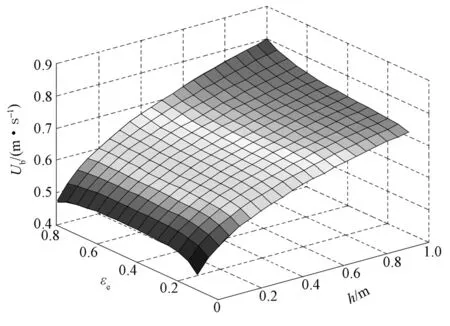
图3 气泡流动速率随床层高度和乳化相空隙率的变化关系Fig. 3 Variation of the velocity of bubbles with bed height and emulsion voidage
由图3可以得知,气泡流动速率随着局部床层高度的上升而逐渐增加,当到达床层顶部区域时,气泡速度逐渐趋于稳定。1)定性分析。气泡在底部生成,从无到有,其初始流动速率显然很小。而当气泡达到床层顶部时,气泡间因合并和破裂过程中相互频繁碰撞而逐步达到平衡,气泡流动速率也因此保持相对稳定。这一变化趋势与实验研究结论是一致的。2)定量分析。采用相同实验条件,以Zou Z.等[14]利用高速摄像机和图像分析技术所测定的气泡速率作为实验值。然而,与之相对应的模拟值却较难确定。由图3可知,模拟计算下的气泡运动速率与乳化相空隙率有关,但乳化相为建立局部结构参数模型而通过系统分解获得,实际情形下并不能严格界定该相。且在同一床层高度下,气泡流动速率随乳化相空隙率的变化不敏感,故采用同高度下不同乳化相空隙率所对应的平均值作为此高度处气泡运动速率的模拟值,其误差分析结果如表2所示。

表2 气泡运动速率的模拟值与实验值结果分析Table 2 A comparison between the simulations and experiments ofUb
分析表2中的数据可知,气泡流动速率的模拟值与实验值呈现出一致性,相对误差均在±10%以内,因而验证了结构曳力模型的正确性。
3.2 表观滑移速率与床层高度和乳化相空隙率
图4描述了气泡相与乳化相间表观滑移速率随局部床层高度和乳化相空隙率的变化关系。
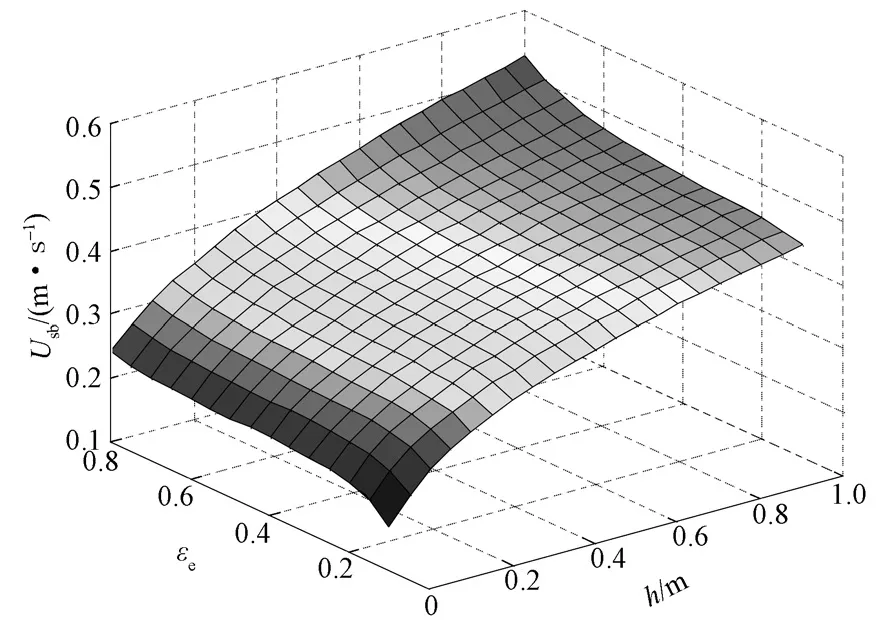
图4 气泡相与乳化相间表观滑移速率随床层高度和乳化相空隙率的变化关系Fig. 4 Variation of the velocity of bubbles with bed height and emulsion voidage
由图4可以得知,表观滑移速率实际上是气泡相相对于乳化相的表观运动速率,因此其变化趋势与图3中的气泡流动速率相同。并且,与乳化相空隙率相比,表观滑移速率受床层高度的影响更为显著。由于气固相间曳力与表观滑移速度的平方成正比,不难得出,曳力随着床层高度的上升急剧增加。因此,在鼓泡床中,位于床层上部颗粒的湍动程度要比下部的剧烈得多。这一结果与实验所观测到的现象相符。
3.3 气泡速率与床层高度和乳化相空隙率
气泡是鼓泡床中典型的介尺度结构,并且气泡的生长、破碎、合并均严重影响着床层中颗粒的流动。图5所示为气泡相的体积分数随局部床层高度及乳化相空隙率的变化趋势。
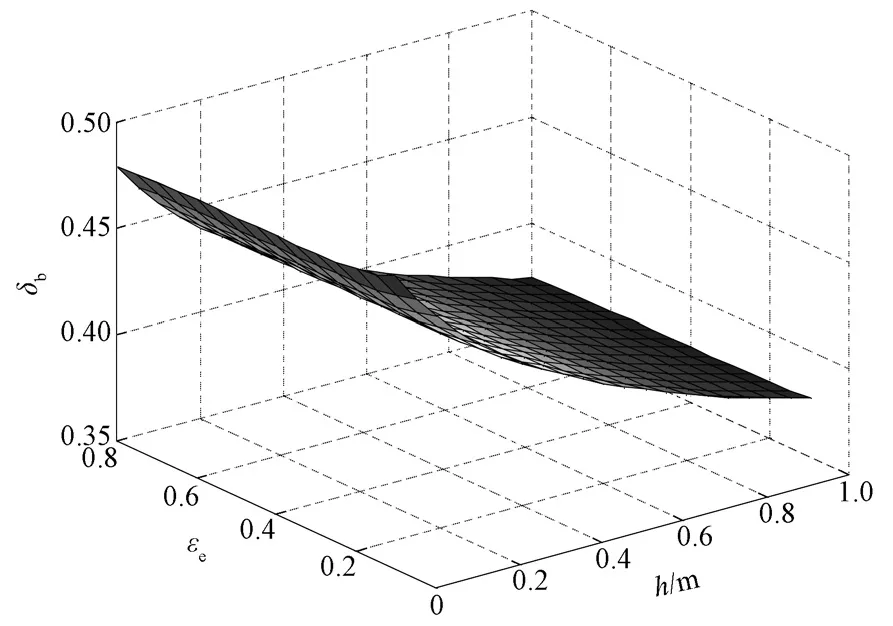
图5 气泡速率随床层高度和乳化相空隙率的变化关系Fig. 5 Theδbvariation with bed height and emulsion voidage
由图5 可以得知,在整个床层内,气泡相的体积分数始终维持在0.38~0.45的范围内,这是“气相控制”和“颗粒控制”两种机制共同作用、相互协调的结果。气相控制是指气流总是趋于选择阻力最小的路径流动,而固相控制是指颗粒总是趋于维持最低的重力势能而向下运动。因此,鼓泡床的流化实质上是颗粒相与气体相的相互“博弈”,最终两者相互“妥协”而使床层呈现出相对稳定的流态化[16]。
3.4 气体流动表观速率与床层高度和乳化相空隙率
图6给出了气泡中气体流动表观速率随乳化相空隙率和床层高度的变化关系。
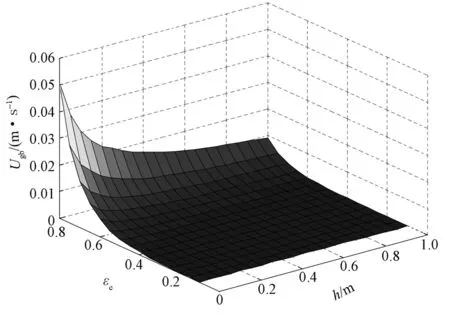
图6 气泡中气体流动表观速率随床层高度和乳化相空隙率的变化关系Fig. 6 The values ofUgbvariation with bed height and emulsion voidage
由图6可以得知,当乳化相的空隙率较小时,无论在床层中的哪个位置,气泡中气体流动表观速率接近于0,说明此时乳化相较浓密,因而其中的气体流动所受阻力较大,具体表现为此时气泡的流动速率大于气体在乳化相中的表观速率。但当乳化相空隙率达到0.5 时,该速率立即增大,但与图3中所示的气泡流动速率相比,此速率仍可以忽略不计。因此,气泡中气体流动表观速率对超细颗粒鼓泡床的流动特性基本没有影响,这与Shi Z.等[8]在不考虑气泡中气体流动表观速率时,仍然可以合理模拟出鼓泡床的床层膨胀情形相吻合。
3.5 颗粒团粒径与床层高度和乳化相空隙率
颗粒聚团作为鼓泡床中介尺度结构的典型代表,其粒径和密度均显著影响着床层的流化质量。据此,Geldart根据颗粒粒径和密度将颗粒分为A、B、C、D 4类。Zhou T.等通过实验测定出表观气速0.32 m/s下,相同粒径的黏性Al2O3颗粒,在鼓泡流化床中的聚团粒径约为167 μm[11]。基于计算模拟分析,在整个床层内颗粒聚团的粒径分布如图7所示。
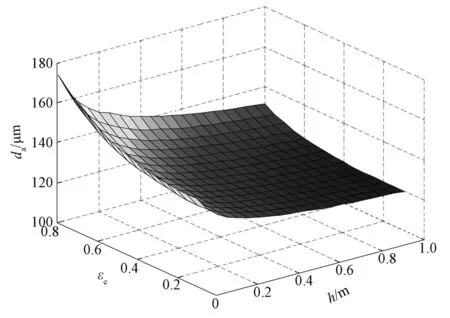
图7 颗粒团粒径随床层高度和乳化相空隙率的变化关系Fig. 7 Thedavariation with height and emulsion voidage
由图7可以得知,聚团粒径的分布范围为 100 ~170 μm,这与实验中所测得的粒径(167 μm)是一致的。一方面,该粒径分布范围归属于Geldart A 类或B类颗粒,足见黏性氧化铝颗粒实际上是以聚团形式流化;另一方面,聚团粒径在很大程度上受床层高度的影响,随着床层高度的上升,聚团粒径逐渐减小。这主要是因为气泡直径随着床层上升而增加,气泡相逐步占据主导地位,颗粒相因而被其削弱,其结果表现为粒径的减小。
4 结语
采用7个结构参数描述了具备复杂多尺度结构的黏性颗粒鼓泡床系统,通过系统分解的手段,使散式流态化中的相关理论也可构建局部结构参数模型。从具体实验算例出发,按照全局搜索算法中的计算程序,利用Matlab对结构参数迭代求解。局部结构模型的评价结果表明,各结构参数能合理恰当地描述黏性颗粒在鼓泡床中的局部流动结构,并且均与文献报道和实验现象吻合。因此,可以用这些结构参数推导和计算复杂非均匀体系的结构曳力模型。
该工作的创新性在于将数值模拟研究从传统的粗颗粒流场延伸到流动结构更复杂的黏性颗粒鼓泡床流场,扩展了数值模拟的应用领域。描述床内非均匀流动的局部结构参数模型的建立,使得黏性颗粒鼓泡床的结构曳力模型建立和流场模拟成为可能。此外,这种建模思路对于其它复杂气固多相流系统的数值模拟工作也具有一定的指导作用。
[1] AMIRI Z,MOVAHEDIRAD S,SHIRVANI M .Particles Mixing Induced by Bubbles in A Gas-Solid Fluidized Bed[J]. Aiche Journal,2016,62(5):1430-1438.
[2] 周 涛,段 昊,唐文江,等. 混合纳米SiO2和纳米TiO2颗粒在添加FCC的流态化研究[J]. 湖南工业大学学报,2014,28(4):1-7.ZHOU Tao,DUAN Hao,TANG Wenjiang,et al. Fluidization Behavior of Mixed SiO2and TiO2Nanoparticles with FCC Particles[J]. Journal of Hunan University of Technology,2014,28(4):1-7.
[3] 徐 宝,周 涛,罗传宝,等. ZnO和CuO混合纳米颗粒在添加FCC粗颗粒的流态化及聚团碰撞与破碎过程研究[J]. 湖南工业大学学报,2016,30(3):63-70.XU Bao,ZHOU Tao,LUO Chuanbao,et al. Research on the Agglomeration Collision and Fragmentation Process in a Fluidized Bed of ZnO and CuO Composite Nanoparticles Added with FCC Coarse Particles[J].Journal of Hunan University of Technology,2016,30(3):63-70.
[4] OMMEN J R V,VALVERDE J M,PFEFFER R.Fluidization of Nanopowders:A Review[J]. Journal of Nanoparticle Research,2012,14(3):737.
[5] WANG Zhaolin,KWAUK Mooson,LI Hongzhong.Fluidization of Fine Particles[J]. Chemical Engineering Science,1998,53(3):377-395
[6] ZOU Zheng,LI Hongzhong,ZHU Qingshan,et al. Experimental Study and Numerical Simulation of Bubbling Fluidized Beds with Fine Particles in Two and Three Dimensions[J]. Industrial & Engineering Chemistry Research,2013,52 (33):11302-11312.
[7] SYAMLAL M,O’BRIEN T. In Computer Simulation of Bubbles in a Fluidized Bed[J]. Aiche Symposium Series,1989,20:22-31.
[8] SHI Zhansheng,WANG Wei,LI Jinghai. A Bubble-Based EMMS Model for Gas-Solid Bubbling Fluidization[J]. Chemical Engineering Science,2011,66 (22):5541-5555.
[10] THOMAS D G. Transport Characteristics of Suspension:VIII. A Note on the Viscosity of Newtonian Suspensions of Uniform Spherical Particles[J]. Journal of Colloid Science,1965,20 (3):267-277.
[11] ZHOU Tao,LI Hongzhong. Estimation of Agglomerate Size for Cohesive Particles During Fluidization[J].Powder Technology,1999,101 (1):57-62.
[12] HORIO M,IWADATE Y. The Prediction of Sizes of Agglomerates Formed in Fluidized Beds[C]//Proceeding 5th World Congress of Chemical Engineering, 2nd Int.Particle Technology Forum. San Diego:[s. n.],1996:722-731.
[13] MAURER S,GSCHWEND D,WAGNER E C,et al. Correlating Bubble Size and Velocity Distribution in Bubbling Fluidized Bed Based on X-Ray Tomography[J].Chemical Engineering Journal,2016,298:17-25.
[14] ZOU Zheng,LI Hongzhong,ZHU Qingshan. The Bubbling Behavior of Cohesive Particles in the 2D Fluidized Beds[J]. Powder Technology,2011,212(1):258-266.
[15] ERGUN S. Fluid Flow Through Packed Columns[J].Chemical Engineering Program,1952,48:89-94.
[16] LI Jinghai,CHENG Congli,ZHANG Zhongdong,et al. The EMMS Model:Its Application,Development and Updated Concepts[J]. Chemical Engineering Science,1999,54 (22):5409-5425.
(责任编辑:廖友媛)
Numerical Simulation of the Local Fluid Texture for Bubbling Fluidized Beds with Cohesive Particles
LUO Chuanbao,ZHOU Tao,WANG Mengdi,NIU Quanliang
(School of Chemistry and Chemical Engineering,Central South University,Changsha 410083,China)
Due to the agglomeration effect between particles, the cohesive particles in the bubbling fl uidized beds(BFBs), mainly in form of particles, agglomerates and multi-scale structures in beds, are more complicated than that of coarse particles in terms of the fl ow characteristics. Therefore, a system decomposition method has been introduced,with the bubble fl uidized bed system with non-uniform fl ow structures divided into three homogeneous subsystems, i.e.the emulsion phase, the bubble phase and the inter-phase phase; and seven structural parameters have been introduced to describe the local fl ow structure of the system. Then a local structural parameter model of the system, based on the force balance model, has been constructed by using the continuity equation, the momentum conservation equation and the empirical formula. Finally, a case study has been made on the fl uidization of the cohesive alumina particles in a bubbling fl uidized bed, followed the global search algorithm used to solve the structural parameters to evaluate the feasibility of the proposed model. The experimental results show that the structural parameters help to correctly re fl ect the local fl ow structure of cohesive particles in a bubbling fl uidized bed, which is consistent with the experimental data.Therefore, the drag force between phases, fl ow fi eld simulation and fl ow characteristics of these structural parameters can be worked out fi nally.
fl uidization;cohesive particle;numerical simulation;local structural parameters model
TQ021.1
:A
:1673-9833(2017)03-0063-06
10.3969/j.issn.1673-9833.2017.03.011
2017-02-23
国家自然科学基金资助项目(21376269),中南大学米塔尔创新科研基金资助项目(MX2016421)
罗传宝(1991-),男,湖南岳阳人,中南大学硕士生,主要研究方向为数值模拟,E-mail:luochuanbao1992@163.com
周 涛 (1963-),男,湖南常德人,中南大学教授,博士生导师,主要从事纳米材料,超微细颗粒的制备和表面改性,多相流与流态化技术方面的教学与研究,E-mail:zhoutao@csu.edu.cn
