基于自适应神经网络的柔性关节机械臂控制

李 光，周鑫林，肖 凡

（湖南工业大学 机械工程学院，湖南 株洲 412007）

基于自适应神经网络的柔性关节机械臂控制

李 光，周鑫林，肖 凡

（湖南工业大学 机械工程学院，湖南 株洲 412007）

柔性关节机械臂系统是一个非线性高阶系统，且其动力学方程难以精确地获得。因此，提出一种以关节驱动电机的输入电压为控制量的自适应神经网络控制器，用于控制多连杆柔性关节机械臂系统。所提控制方法通过对柔性关节机械臂模型解耦得到关节转角关于电压的方程，以电压为系统控制输入。设计神经网络控制器用于逼近最优控制输入，并设计鲁棒控制器补偿逼近误差。该控制方法不再涉及复杂的动力学方程，因此能简化计算。相比已有控制方法，所提出的控制策略更简单、响应更快且更有效。并以二连杆柔性关节机械臂为例进行了仿真研究，结果证明了所提出控制方法的有效性。

柔性关节机械臂；神经网络；非线性；关节柔性

1 研究背景

在机械臂控制领域，常用机械臂关节处的力矩为系统的控制量，对机械臂系统进行控制。这些控制方法包括PID控制法、反馈线性化控制法。其中，PID控制法的响应速度较慢，且高阶系统不易稳定；反馈线性化控制法则要求系统的状态量必须能监测，因而其控制器算法相对复杂[1]。可见，已有的这些方法不适用于柔性关节机械臂的控制，因柔性关节机械臂的系统模型是一个多输入多输出的高阶非线性系统，其动力学方程复杂且计算量大。

柔性关节机械臂的电压控制方法是一种新的控制方法[2]，其主要特点在于建立了关节转角关于机械臂驱动电机电压的方程，因而避免了动力学方程带来的不利影响，简化了计算。在基于电压输入的柔性机械臂控制研究中，文献[3]提出了一种鲁棒自适应控制，其在机械臂模型不确定的情况下也能得到良好的跟踪效果。文献[4]提出了一种鲁棒跟踪控制方法，并通过引入不确定项得到控制率，其优点在于无需明确的机械臂动力学模型。

本研究拟结合电压控制方法和神经网络控制，设计一种自适应神经网络控制器，为柔性关节机械臂的电压控制提供一定的理论参考。本研究利用神经网络可对任意非线性函数逼近的特点，对最优控制输入在线逼近。因所提方法不涉及复杂的动力学方程，使得控制率较为简单，能够快速响应且迅速逼近期望值。其次，神经网络的网络权值、中心值以及宽度值由相应的自适应率调整，并且使用Lyapunov函数验证控制算法的稳定性。

2 柔性关节机械臂动力学模型

永磁直流电机驱动的n连杆柔性关节机械臂的动力学方程可表述如下[5]：

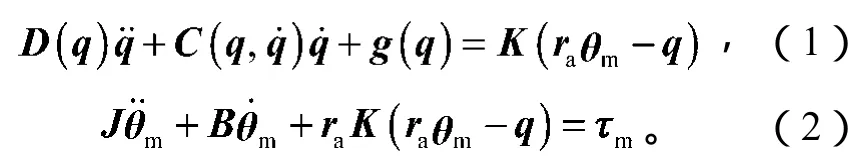
式（1）和（2）中：

D(q)为n阶惯性矩阵项，且D(q)∈Rn；

g(q)为重力项，且g(q)∈Rn；

θm为电机转子转角向量，且θm∈Rn；

q为关节角度向量，且q∈Rn；

J为电机惯性项，B为电机阻尼项，ra为传动系统减速比，均为n阶对角矩阵；

K为关节的刚度矩阵，且为对角矩阵；

τm为电机力矩向量，且τm∈Rn。

电枢电压平衡方程如式（3）所示[5]：

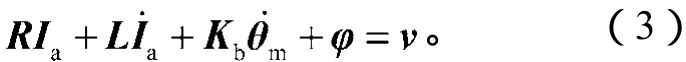
式中：R为电枢阻抗项，L为电枢电感项，均为n阶对角矩阵；

v为电机电压向量，且v∈Rn；

Ia为电机电流向量，且Ia∈Rn；

Kb为反电动势系数，且Kb∈Rn；

φ代表外部干扰项，且φ∈Rn。

电机转矩与电机电流的关系如式（4）所示[5]：

式中Km为电机转矩常数的对角矩阵。

根据电压控制理论，以电压向量v为系统输入向量，关节角度向量q为系统输出向量，据式（1）～（4）可得机械臂系统的状态空间模型，见式（5）[5]。

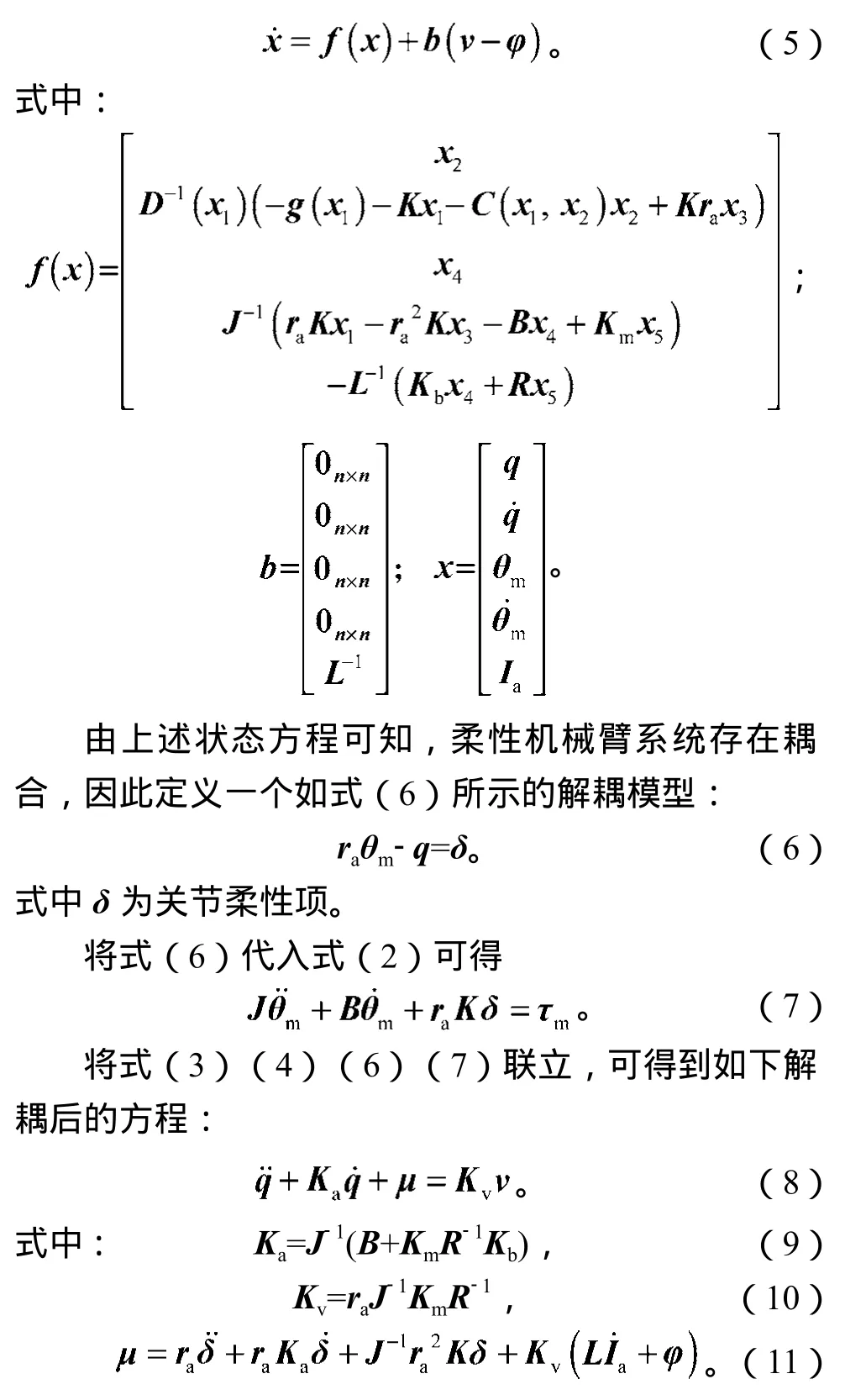
3 神经网络控制器设计

神经网络算法已经成为人工智能的一个重要研究方向，适用于高度非线性以及具有不确定性的被动控制系统。神经网络能逼近任意非线性函数，且具有自主学习性，能够不断地调整结构参数。

本研究采用3层神经网络逼近系统控制输入，其基函数的中心值和宽度可以调整，神经网络的结构如图1所示。

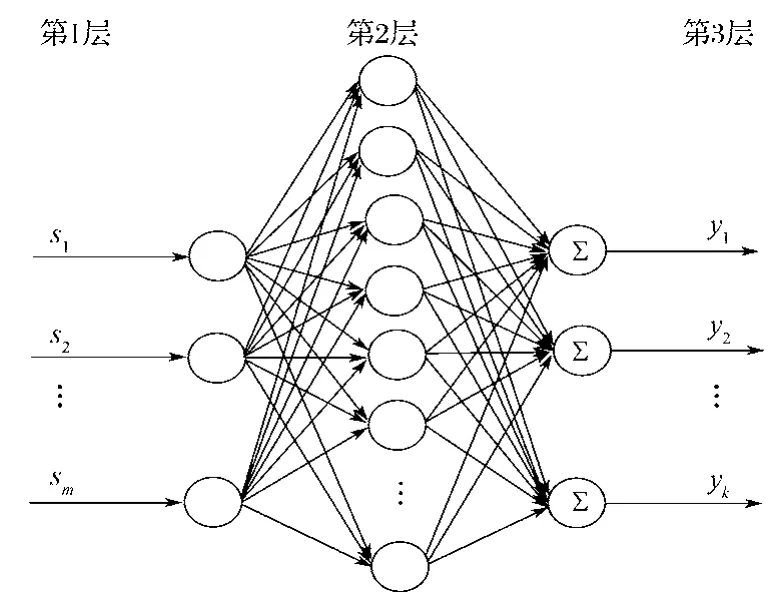
图1 RBF神经网络结构Fig. 1 RBF neural network structure

第一层 输入层，si（i=1, 2，…，m）为神经网络输入；

第二层 隐含层，选取如式（12）所示的高斯基函数，

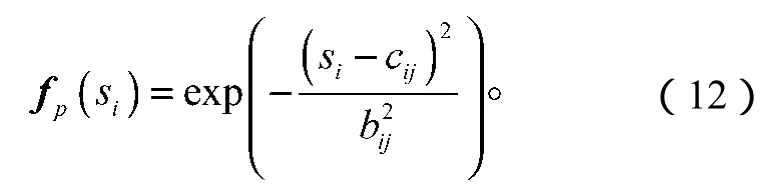
式中：

fp(si)为隐含层节点输出，p=1, 2, …,l；

cij和bij分别为高斯基函数的中心值和宽度，其中i=1, 2, …,m，j=1, 2, …,n。

则基函数中心值和宽度向量分别为

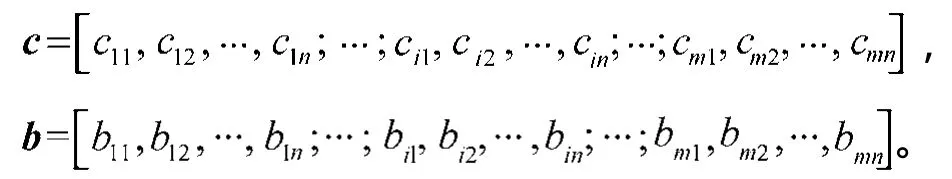
第三层 输出层，y为神经网络输出，且

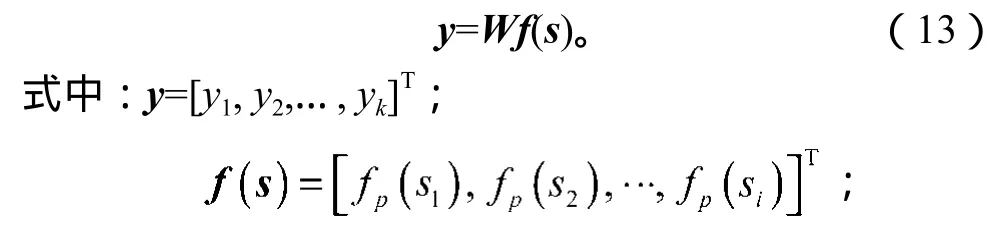
W代表神经网络的权值，且W∈Rk×i。

假设机械臂的关节转角q及其角速度可测，由此可得关节转角误差e和角速度误差。则以e作为神经网络的输入，电压v作为其输出，可设计自适应神经网络控制器以使得机械臂关节转角q能够跟踪期望值qd。

式（29）～（31）中η1、η2、η3和η4为常数。

定理1 对于解耦后的多连杆柔性关节机械臂系统（8），采用控制器（21），设计神经网络参数自适应率（29）和鲁棒控制器（30），能够保证系统的渐进稳定性。

4 仿真分析

以二连杆柔性关节机械臂为仿真对象，连杆为匀质刚性杆进行仿真分析，系统各参数取值如下：各连杆的关节刚度为k1=k2=500 N·m/rad，各连杆的长度为l1=l2=1.0 mm，各连杆的质量为m1=m2=1.0 kg，驱动电机的电枢电阻为R1=R2=1.6 Ω，驱动电机的转子转动惯量为J1=J2=0.000 2 kg·m2，驱动电机的黏性阻尼系数为B1=B2=0.001，驱动电机力矩常数为0.26，期望轨迹数为qd=[sin(t)，cos(t)]。且η1=25，η2=5，η3=2，η4=0.5。神经网络隐含层节点数为7，高斯基函数的中心值、宽度值初始值如下：

如上条件下所得仿真结果如图2所示。

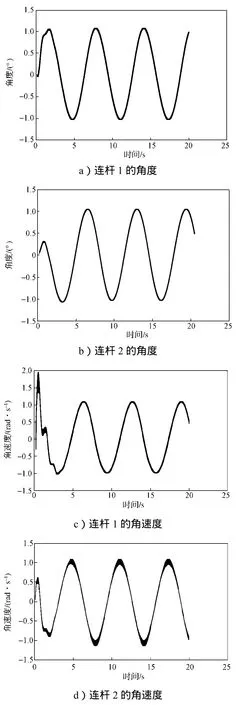
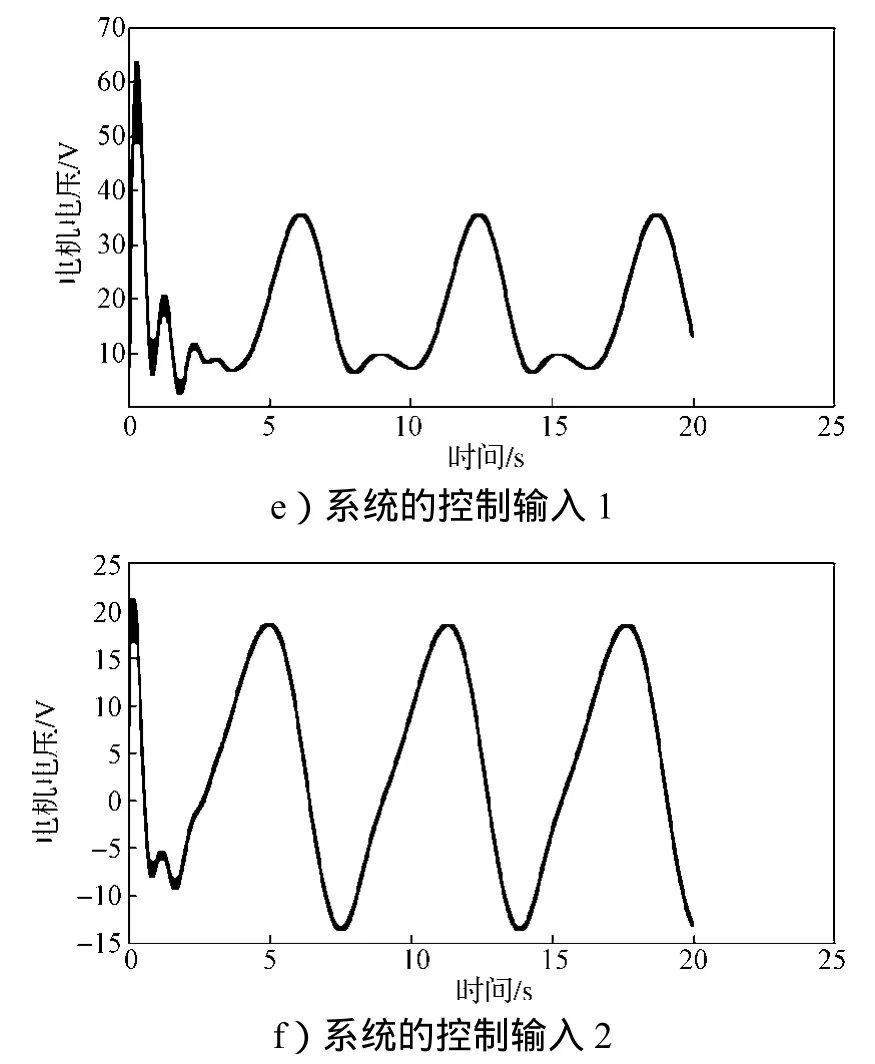
图2 自适应神经网络控制器仿真结果Fig. 2 Simulation results of adaptive neural network controllers

图2a和b分别为连杆1、2的关节转角跟踪，图2c和d分别为连杆1、2的角速度跟踪，图2e和f分别为连杆1、2的控制输入。对照图a、b、c、d可知，自适应神经网络控制器能够逼近控制输入且精确地跟踪期望轨迹。由图e和f可知，控制输入曲线光滑连续，振荡小。仿真结果表明，所提出的控制方法可实现对关节期望轨迹的快速跟踪。

5 结语

本文针对柔性关节机械臂提出一种自适应神经网络控制器，通过对柔性关节机械臂模型的解耦，得到电机电压与连杆转角的动力学模型。在此基础上设计了自适应神经网络控制器，即采用基函数中心值和宽度值能自适应调整RBF神经网络逼近模型。使用Lyapunov理论证明了系统的闭环稳定性，并以二连杆柔性关节机械臂为例进行了系统仿真。仿真结果表明，本文提出的控制方法可实现关节对期望轨迹的快速跟踪，且对关节柔性进行了有效的抑制，控制输入无冲击，输入曲线光滑。

[1] 黄 华. 柔性关节机械臂的建模及控制研究[D]. 株洲：湖南工业大学，2014.HUANG Hua. A Research on Modeling and Control of Flexible-Joint Robots Arm[D]. Zhouzhou：Hunan University of Technology，2014.

[2] FATEH M M. On the Voltage-Based Control of Robot Manipulators[J]. International Journal of Control，Automation and Systems，2008，6(5)：702-712.

[3] FATEH M M. Nonlinear Control of Electrical Flexible Joint Robots[J]. Nonlinear Dynamics，2012，67(4)：2549-2559.

[4] FATEH M M. Robust Control of Flexible-Joint Robots Using Voltage Control Strategy[J]. Nonlinear Dynamics，2012，67(2)：1525-1537.

[5] FATEH M M，SOUZANCHIKASHANI M. Decentralized Direct Adaptive Fuzzy Control for Flexible-Joint Robots[J]. Control Engineering and Applied Informatics，2013，15(4)：97-105.

[6] WAI R J，CHANG C J. Tracking Control Based on Neural Network Strategy for Robot Manipulator[J].Neurocomputing，2003，51(7/8/9)：425-445.

[7] 徐智浩，李 胜，张瑞雷，等. 基于Lu Gre 摩擦模型的机械臂模糊神经网络控制[J]. 控制与决策，2014，29 (6) ：1097-1102.XU Zhihao，LI Sheng，ZHANG Ruilei，et al. Fuzzy-Neural-Network Control for Robot Manipulators with Lu Gre Friction Model[J]. Control and Decision，2014，29(6)：1097-1102.

[8] 李 光，符 浩. 无模型机械臂BP神经网络状态观测及反演跟踪控制[J]. 中国机械工程，2016，27(7)：859-865.LI Guang，FU Hao. BP Neural Network State Observation and Backstepping Tracking Control of Model-Free Robotic Manipulators[J]. China Mechanical Engineering，2016，27(7)：859-865.

[9] LIMA J J，ROCHA R T， JANZEN F C. Position Control of a Manipulator Robotic Arm Considering Flexible Joints Driven by a DC Motor and a Controlled Torque by a MR-Brake[J]. International Mechanical Engineering Congress and Exposition，2016，4B：1-10.

[10] GAO L，CHEN Q，SHI L. Adaptive Neural Output Feedback Control for Flexible-Joint Robotic Manipulators[C]//Proceedings of 2016 Chinese Intelligent Systems Conference. Singapore：Springer，2016：629-640.

（责任编辑：廖友媛）

Control of Flexible-Joint Robots Based on Adaptive Neural Networks

LI Guang，ZHOU Xinlin，XIAO Fan
（School of Mechanical Engineering，Hunan University of Technology，Zhuzhou Hunan 412007，China）

The flexible-joint manipulator system is a nonlinear high-order system. It is difficult to obtain the kinetic equation accurately. A proposal has been made of an adaptive neural network controller based on the input voltage of the joint drive motor, with its application for the control of the multi-link fl exible-joint manipulator system.By adopting the proposed control method, the equations of the joint angle can be obtained by decoupling the fl exible joint manipulator model, with motor voltage the inputs of the manipulator system. A neural network controller is designed to approximate the optimal control input, and a robust controller is designed to compensate the approximation error. The control method does not involve complex dynamic equations, thus greatly simplifying the process of calculation. As a result, the proposed control strategy, compared with the existing control methods, is simpler, faster and more ef fi cient. A simulation test has been carried out on the two-link fl exible-joint manipulators, thus verifying the effectiveness of the proposed control method.

fl exible-joint manipulator；neural network；nonlinearity；joint fl exibility

TP241.3

：A

：1673-9833(2017)03-0048-05

10.3969/j.issn.1673-9833.2017.03.008

2017-02-16

李 光（1963-），男，湖北孝感人，湖南工业大学教授，博士，主要从事复杂机电一体化系统建模和控制研究，E-mail ：liguanguw@126.com

周鑫林（1992-），男，湖南怀化人，湖南工业大学硕士生，主要研究方向为机械臂系统控制理论，E-mail：zhouxinlin806@163.com