基于单基频交叉S变换的电压凹陷源定位

杨晓芳，易吉良，程 焰，周 曼，刘小文

（湖南工业大学 电气与信息工程学院，湖南 株洲 412007）

基于单基频交叉S变换的电压凹陷源定位

杨晓芳，易吉良，程 焰，周 曼，刘小文

（湖南工业大学 电气与信息工程学院，湖南 株洲 412007）

电压凹陷扰动源相对于监测点的精确定位，有助于明确供用电双方的责任。为了精确定位电压凹陷扰动源，提出了一种基于单基频交叉S变换的扰动功率定位方法。首先，将监测点采集到的电压、电流信号进行单基频S变换，得出电压、电流的基频复向量；然后，将电压、电流基频复向量经单基频交叉S变换后，求模提取瞬时视在功率，进而求得瞬时视在扰动功率；最后，利用扰动功率判据实现对电压凹陷扰动源的定位。通过对由短路故障、异步电动机启动、变压器励磁涌流以及故障自清除引起的4种典型的电压凹陷源进行建模仿真，对8个监测点进行分析判断，结果证明了所提出方法的准确有效性。

单基频交叉S变换；扰动功率；电压凹陷；定位

0 引言

电压凹陷是指供电电压均方根值在短时间内突然下降至额定电压幅值的90%～10%、典型持续时间为10 ms～1 min的一种现象[1]。电压凹陷不仅会造成电压敏感设备不能正常工作[2]，而且会给企业生产带来重大的经济损失。对电压凹陷源的定位有助于划分供用电双方的责任，为电压凹陷治理提供依据，对提高电能质量具有重要意义。

国内外学者针对电压凹陷定位方法做了大量工作，取得了较多成果[3-4]。其中的扰动功率和能量法，最先是由A. C. Parsons等[5]于2000年提出的，但其只能定位系统释放能量的扰动。此后，张文涛等[6]对其进行了改进，提出了可以定位向系统注入能量的扰动方法，可对电压暂降和电压脉冲两类暂态扰动进行定位，但是没有验证所提方法对其他暂态扰动的有效性，因而适用性不广。

单基频交叉S变换（single fundamental frequency cross S-transform，SFCST）只需要对基波频率点进行运算，因而缩短了运算时间。因此，本研究拟采用SFCST来计算瞬时视在功率，直接利用基频电压、电流复向量，经过交叉S变换得到瞬时视在功率，进而采用扰动功率法实现电压凹陷扰动源的准确定位，并通过对几种典型的电压凹陷[7]仿真实验来验证该方法的准确性，以期为电压凹陷源的准确定位提供理论参考。

1 SFCST变换原理

1.1 S变换

S变换[8]是基于短时傅里叶变换与小波变换的可逆的时频分析方法。设信号h(t)∈L2(R)，其中L2(R)表示实域上的平方可积空间，则h(t)的一维连续S变换S(τ,f)可定义如下：

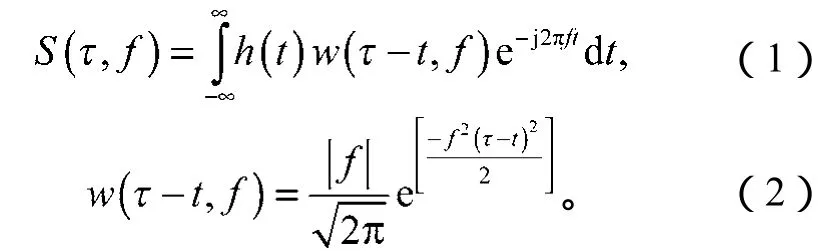
式（1）（2）中：t为时间；f为频率；w(τ-t,f)为高斯窗函数；τ为高斯窗的中心。

利用卷积定理，有

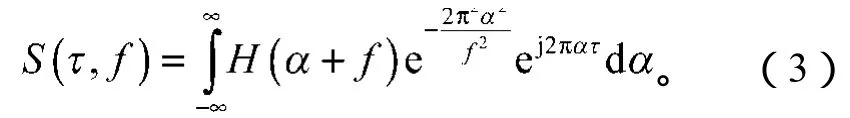
式中：H(α+f)是由信号h(t)的傅里叶变换H(f)经过平移得到的；α为时域内变量τ在频域里的表示。

离散形式的S变换表达式 (f→，τ→kT) 为：

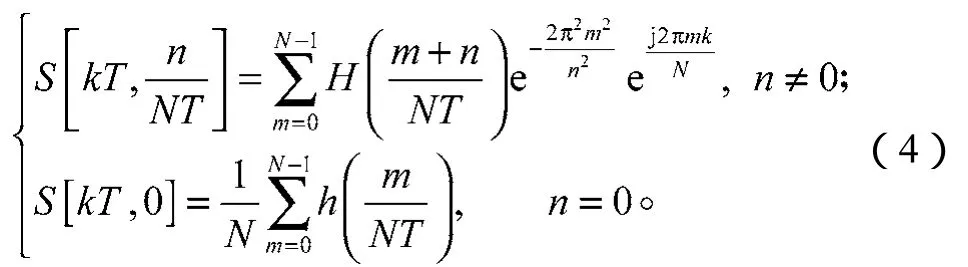
式中：T为采样时间；N为总采样点数；m为时域内时间变量t的离散化形式；k、n分别为时间采样点和频率采样点，且k、n=0, 1, 2, …,N-1。

1.2 单基频S变换

对信号进行S变换时，需要计算各频率点下的加高斯窗的快速傅里叶变换（fast Fourier transform，FFT），计算过程较为繁琐，运算量较大。在进行电压凹陷信号分析时，只需要提取基频f0的相关向量信息，因此由S变换简化的单基频S变换（single fundamental frequency S-transform，SFST）可定义如下：

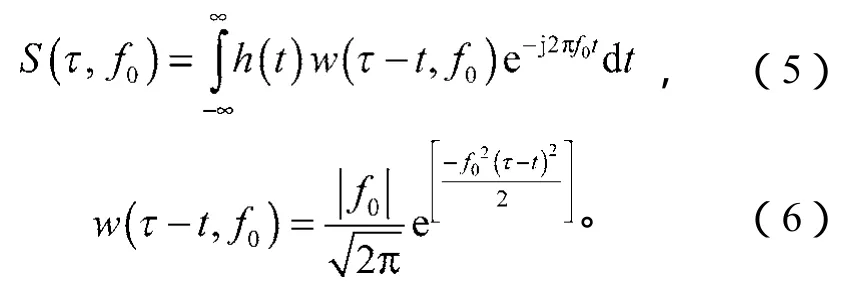
离散化的单基频S变换为：

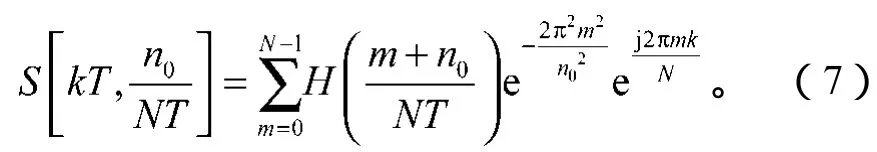
式中n0为基频频率采样点。

可见，信号经单基频S变换后得到的是一维复数向量。

单基频S变换的计算过程如图1所示。

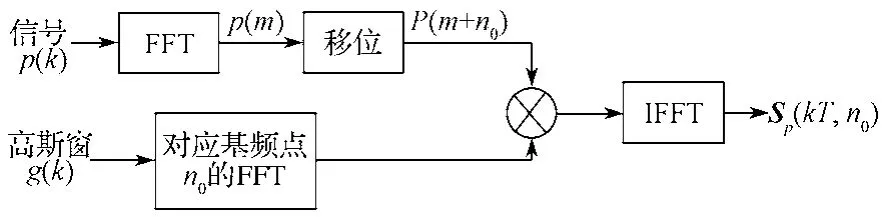
图1 SFST的计算过程Fig. 1 Calculation procedure of single fundamental frequency S-transform

图1中的p(k)为采样信号p(t)的离散形式，将其经快速傅里叶变换后得到p(m)；将p(m)移位n0后得到P(m+n0)；g(k)是高斯窗的离散形式，其对应于基频点的FFT为G(n0,m)；将G(n0,m)与P(m+n0)相乘，再求快速傅里叶逆变换（inverse fast Fourier transform，IFFT）即可以得到基频电压、电流复向量Sp(kT,n0)。

1.3 SFCST原理

电压、电流信号的单基频交叉S变换[9]的定义为

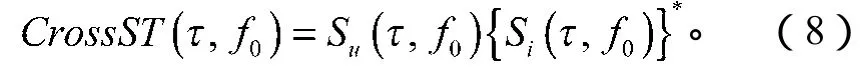
式中：Su(τ,f0)为电压的SFST变换；Si(τ,f0)为电流的SFST变换；{Si(τ,f0)}*为对Si(τ,f0)取共轭。

因电压电流信号的单基频S变换的模与信号的幅值有直接对应关系，故对式（8）求模后便可得到信号的瞬时视在功率。

为简化公式，将CrossST(τ,f0)记为CST(τ,f0)。则单基频交叉S变换的离散形式为

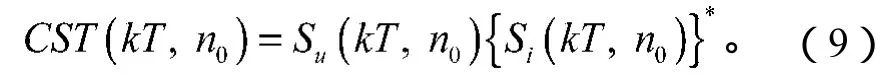
单基频交叉S变换计算过程如图2所示。

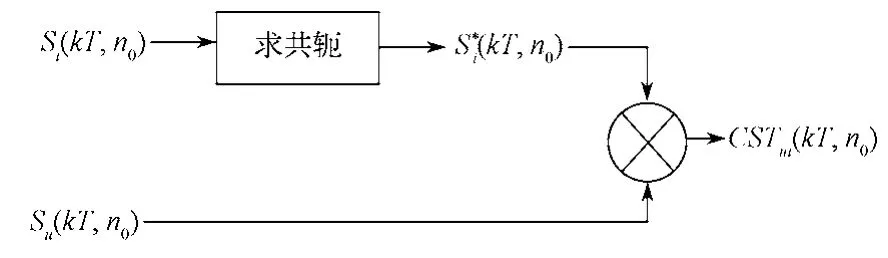
图2 SFCST的计算过程Fig. 2 Calculation procedure of single fundamental frequency cross S-transform

具体计算过程如下：1）将电压、电流信号经SFST后得到Si(kT,n0)和Su(kT,n0)；2）将Si(kT,n0)求共轭，然后与Su(kT,n0)相乘，得到交叉S变换CSTui(kT,n0)；3）对CSTui(kT,n0)求模，即可得到视在功率。

2 基于SFCST和扰动功率的电压凹陷扰动源定位方法

2.1 电压凹陷扰动源的定位原理

本文采用扰动功率法实现对电压凹陷扰动源的定位。扰动功率法的基本思想是当系统发生扰动时，通过监测点处功率或者能量的变化来判断扰动源相对于监测点的位置[10]。对电压凹陷扰动源的定位见图3。

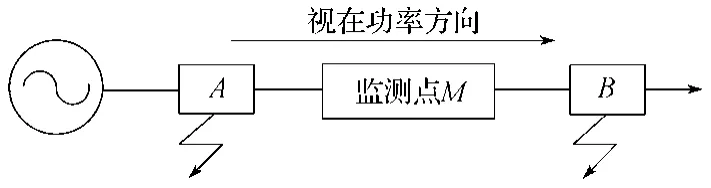
图3 电压凹陷扰动源定位示意图Fig. 3 A sketch map of voltage sag disturbance source location

它以视在功率方向为参考方向，如扰动发生在监测点的后方，如图3中B点，即认为扰动源发生在监测点的上游；否则，如扰动发生在监测点的前方，如图3中A点，即认为扰动源在监测点的下游[11]。

电路发生扰动时，定义三相总功率与系统无扰动时应有的三相总功率的差为扰动功率[5]。本研究利用瞬时扰动视在功率与稳态时的视在功率差得到扰动功率DS。

对称三相电路中，三相总瞬时视在功率S(t)为

式中：UA(t)为A相电压的瞬时值；IA(t)为A相电流的瞬时值。

利用SFCST计算瞬时视在功率的公式为

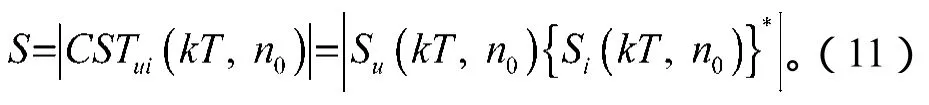
利用SFCST计算的扰动视在功率DS为：

式中：SD为瞬时视在功率；SS为稳态时的三相瞬时视在功率，为一近似常数。

2.2 基于SFCST的电压凹陷扰动源定位法

图4所示为基于SFCST的电压凹陷扰动源定位流程图。

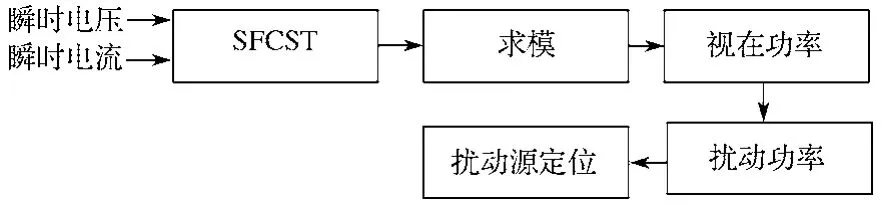
图4 基于单基频交叉S变换的电压凹陷扰动源定位Fig. 4 Voltage sag disturbance location based on single fundamental frequency cross S-transform

电压凹陷扰动源定位过程为：首先，将监测点测量到的瞬时电压、瞬时电流经SFST后，得到单基频电压、电流向量；再对单基频电压、电流经SFCST后求模，得到瞬时扰动视在功率；最后，利用式（12）求出扰动功率DS。

由于暂态扰动的存在，瞬时视在功率SD不可能等于稳态时的三相瞬时视在功率SS，据式(12)可知DS不为零。因此，采用如下扰动功率定位法判据：

1）若DS＞0，则扰动源位于监测点的下游；

2）若DS＜0，则扰动源位于监测点的上游。

3 仿真分析

实际应用中，常见的4种电压凹陷分别是由短路故障、异步电动机启动、变压器励磁涌流以及故障自清除引起的[12]。本研究对这4种电压凹陷进行建模仿真，并利用SFCST和扰动功率定位法实现对扰动源的定位，最后通过判断定位结果与实际情况是否相符来验证该方法的准确性。

3.1 短路故障引起的电压凹陷扰动源定位

图5为三相短路故障系统仿真图。系统频率为50 Hz，变压器T1量程为110/10.5 kV，变压器T2量程为10.5/0.4 kV；采样时间为0.4 s，电压凹陷起止时刻分别为0.05 s和0.18 s。监测点为M1和M2。当系统发生三相短路故障时，监测点M1和M2处的A相凹陷电流和电压波形、经SFCST的基波电压和电流波形及扰动功率波形见图6和7。由图6可知，M1处DS＞0，根据扰动功率定位法判据可知，扰动源发生在M1点的下游。由图7可知，M2处DS＜0，根据扰动功率定位法判据得知扰动源位于M2的上游。

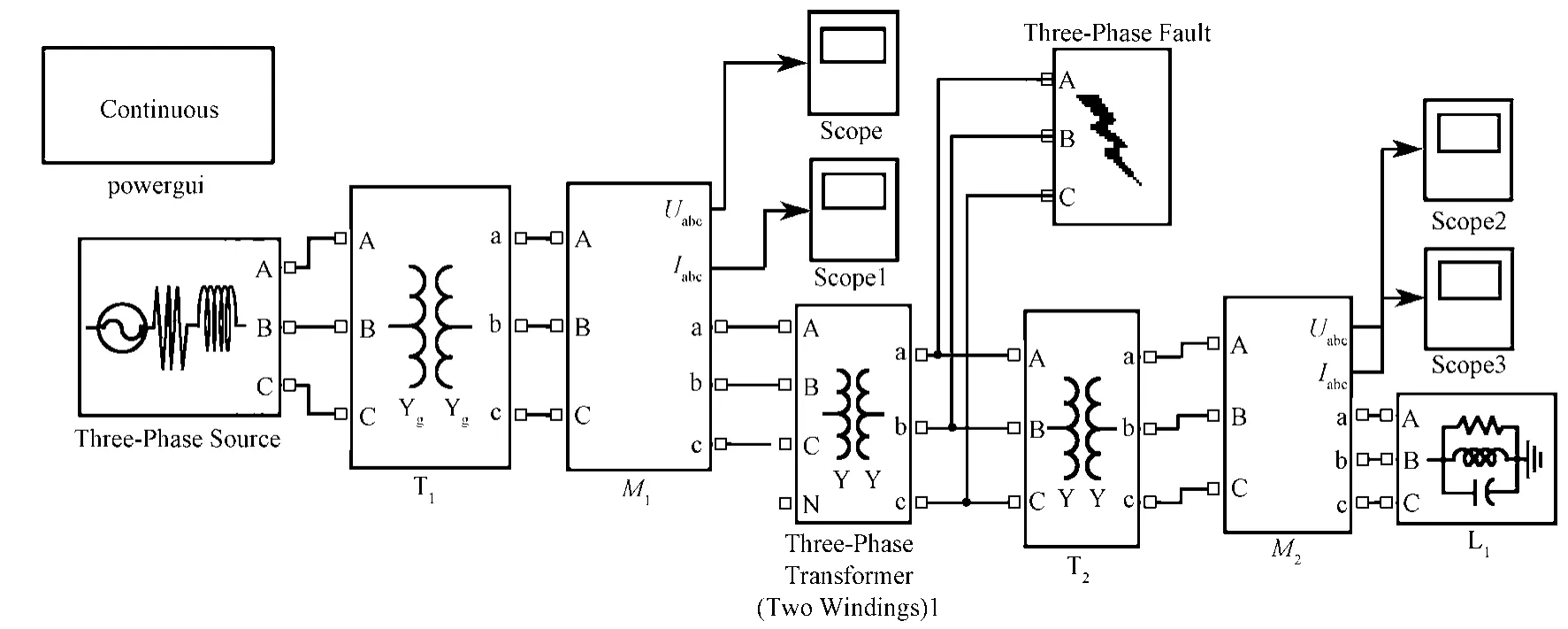
图5 三相短路故障系统Fig. 5 Three-phase short trouble system

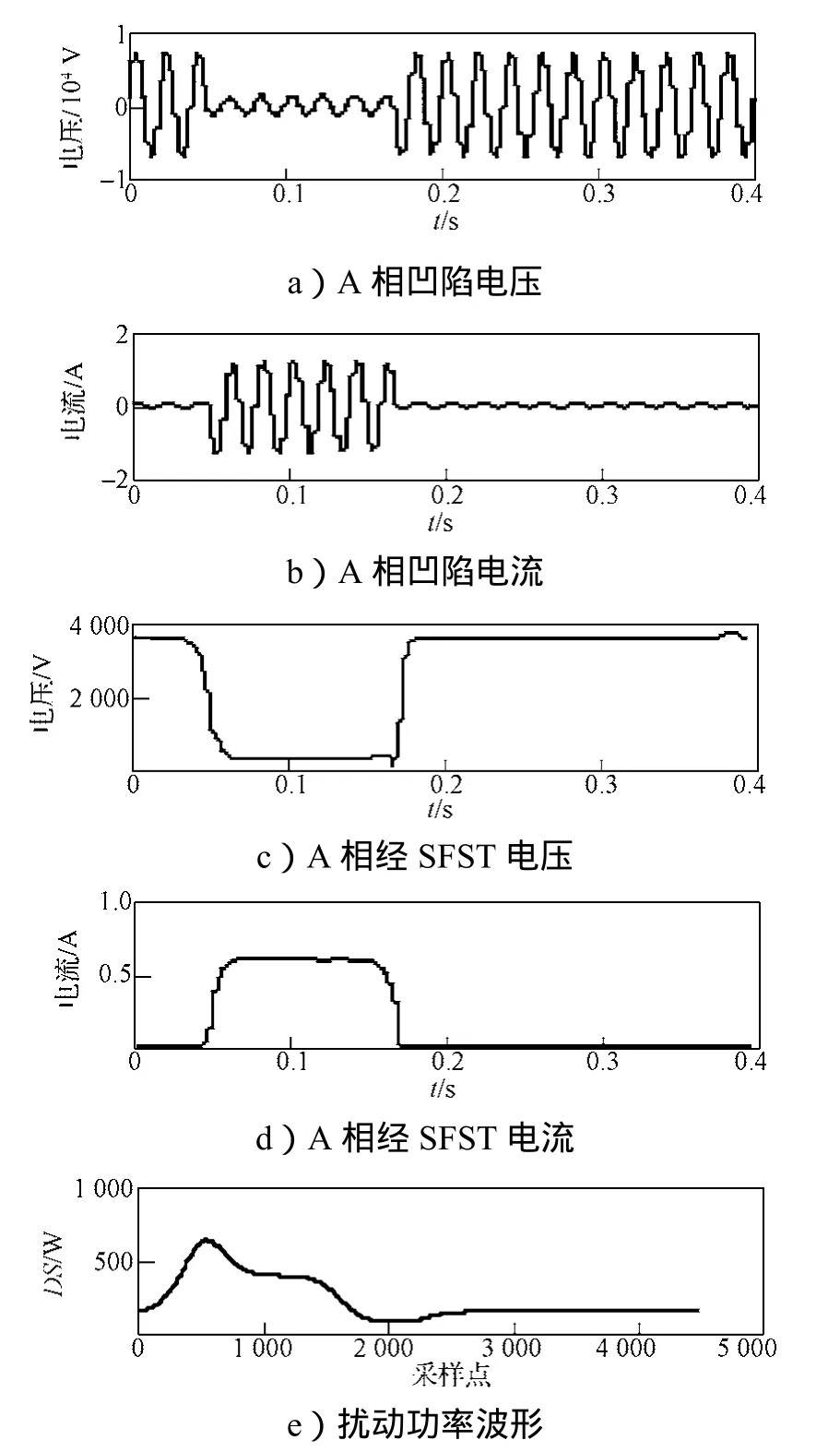
图6 三相短路故障引起的M1点电压凹陷源定位波形图Fig. 6 Voltage sag source location ofM1caused by three-phase short trouble waveform

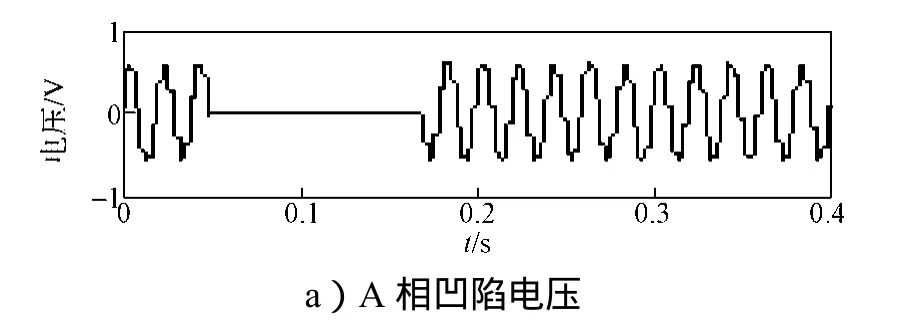
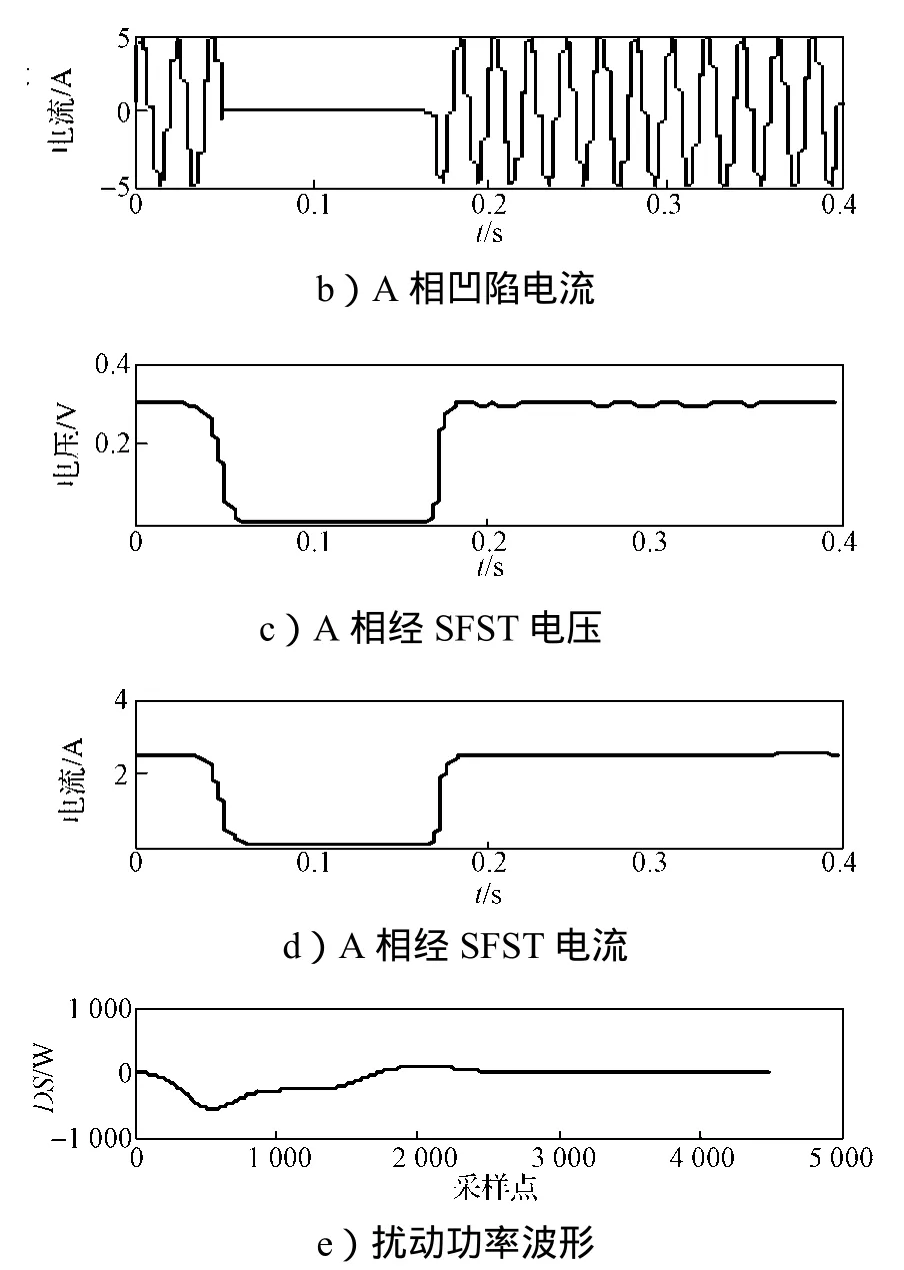
图7 三相短路故障引起的M2点电压凹陷源定位波形图Fig. 7 Voltage sag source location ofM2caused by three-phase short trouble waveform

3.2 异步电动机启动引起的电压凹陷扰动源定位

图8为异步电动机启动仿真图，其系统频率为50 Hz，电源为11 kV，电动机转速为1 460 r/min，PN=75 kW。监测点为M3和M4。异步电动机启动引起电压凹陷时，仿真监测点M3和M4处的A相凹陷电压和电流波形、经SFCST的基波电压和电流波形以及扰动功率波形如图9和10所示。从图9中可以看出，M3点处的DS＞0，根据扰动功率定位法判据可知，扰动源发生在M3点的下游；从图10中可以看出，M4点处的DS＜0，因而扰动源位于M4的上游。

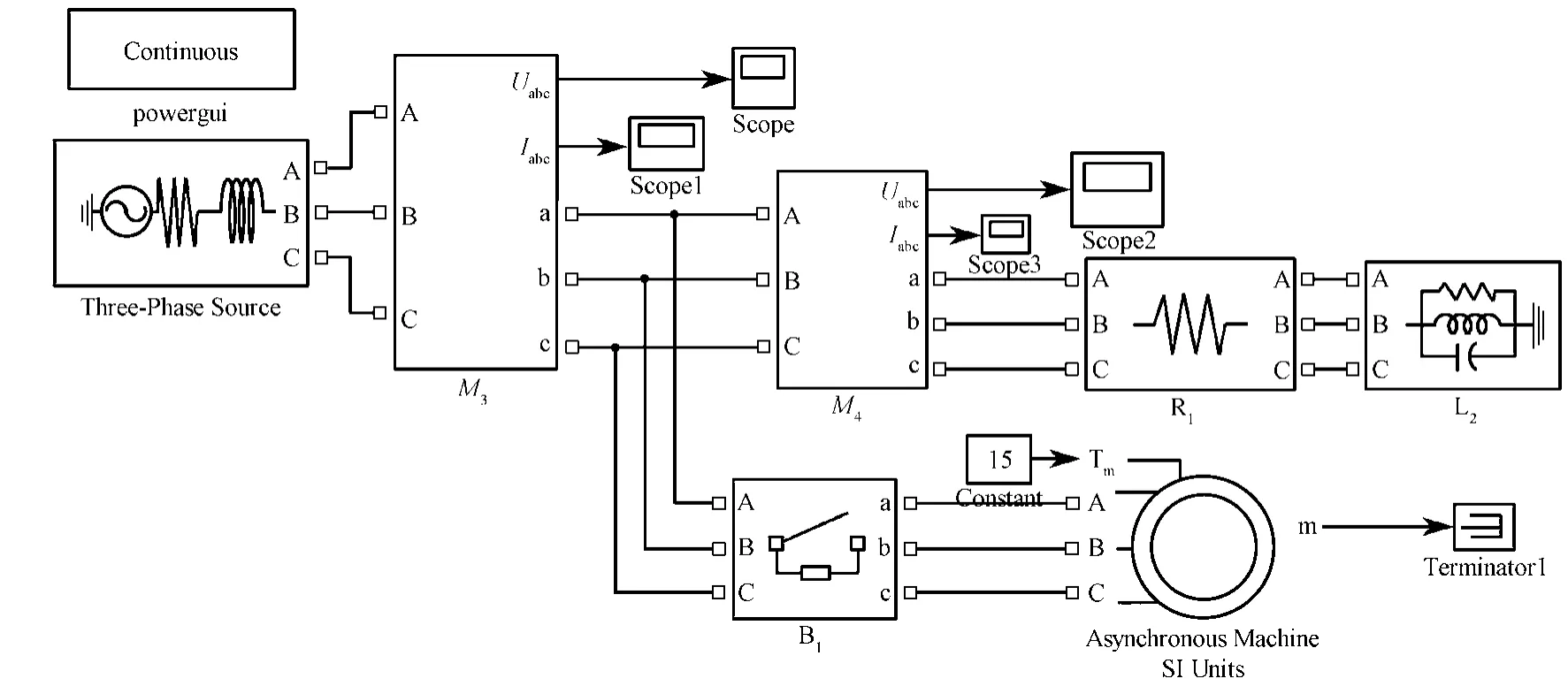
图8 异步电动机启动模型Fig. 8 Starting model of asynchronous motors

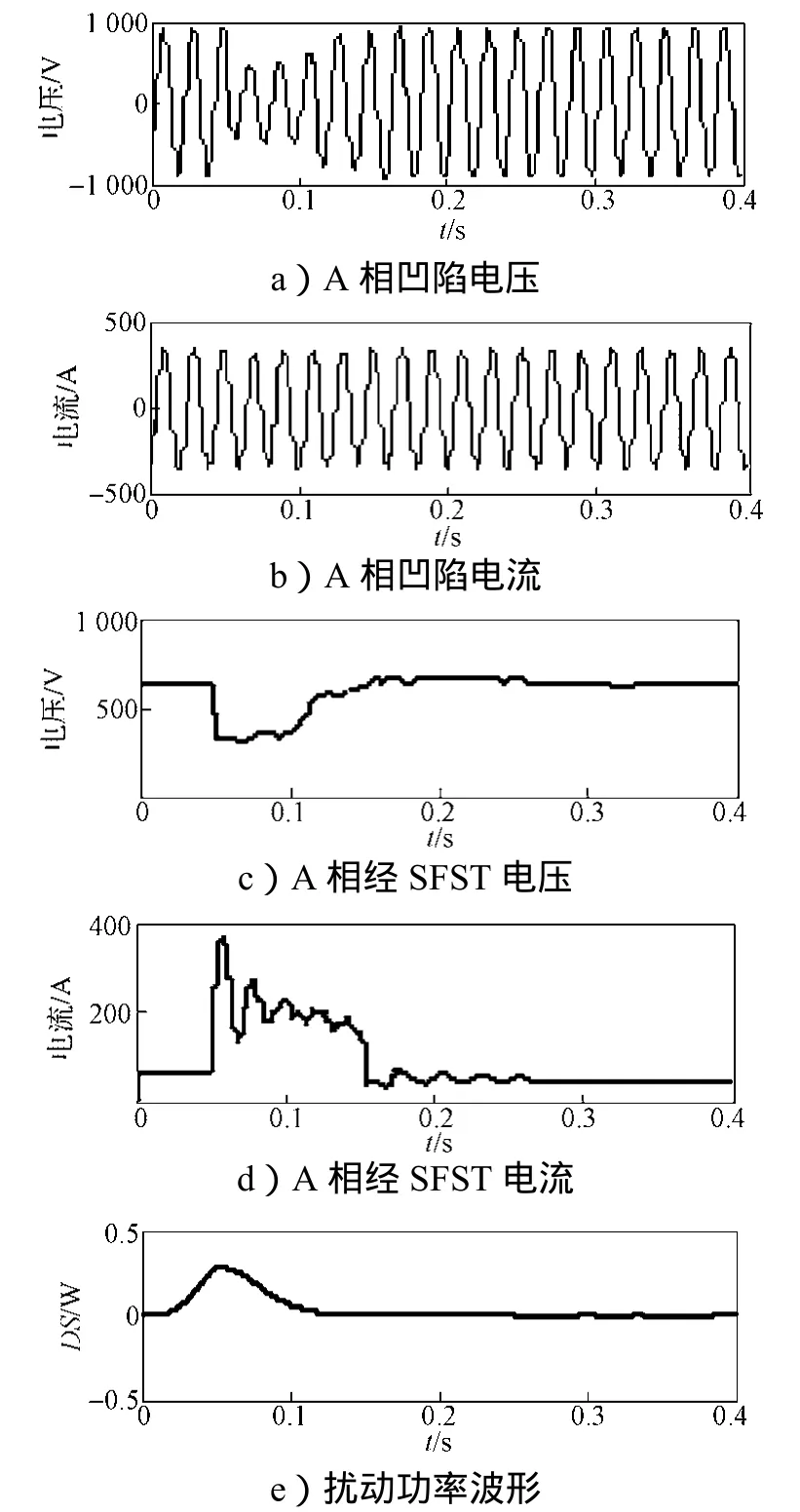
图9 异步电动机启动引起的M3点电压凹陷源定位波形图Fig. 9 Voltage sag source location ofM3caused by the starting of asynchronous motor waveform

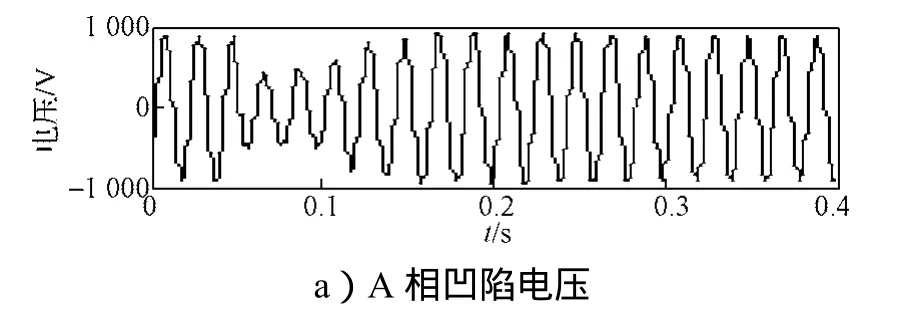
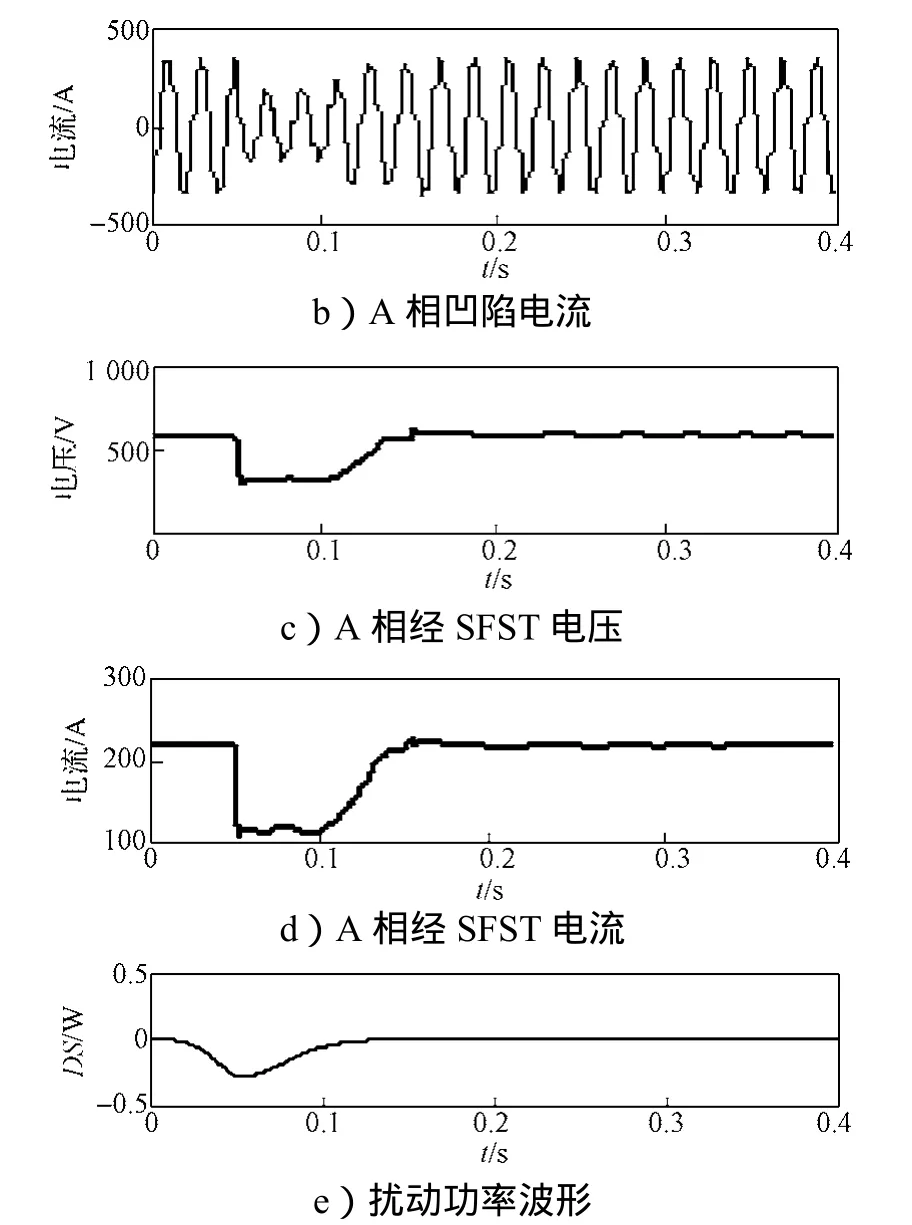
图10 异步电动机启动引起的M4点电压凹陷源定位波形图Fig. 10 Voltage sag source location ofM4caused by the starting of asynchronous motor waveform

3.3 变压器励磁涌流引起的电压凹陷扰动源定位

图11所示为变压器励磁涌流的仿真图。仿真时的系统频率为50 Hz，三相电源电压为11 kV，容量为30 MVA；变压器T3的量程为11/0.4 kV，采用Δ/Yg型接线方式；仿真时间为0.4 s。监测点为M5和M6。变压器励磁涌流引起电压凹陷时，仿真监测点M5和M6处的A相凹陷电压和电流波形、经SFCST的基波电压和电流波形以及扰动功率波形如图12和13所示。

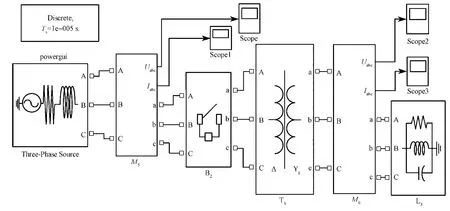
图11 变压器励磁涌流仿真模型Fig. 11 A simulation model of inrush exciting current of transformers

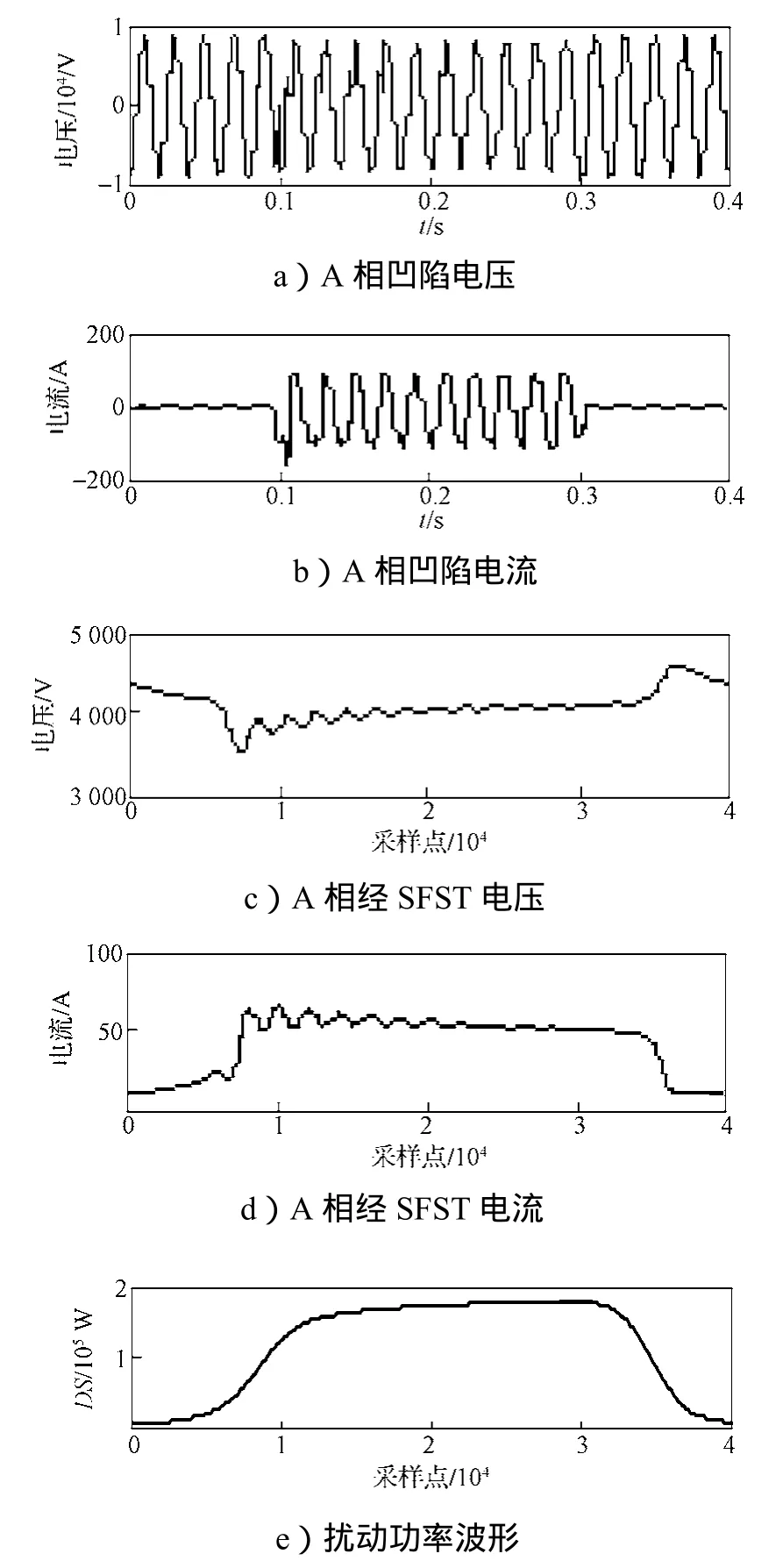
图12 变压器励磁涌流电压M5点凹陷扰动源定位波形图Fig. 12 Voltage sag disturbance source location ofM5caused by inrush exciting current of transformer waveform

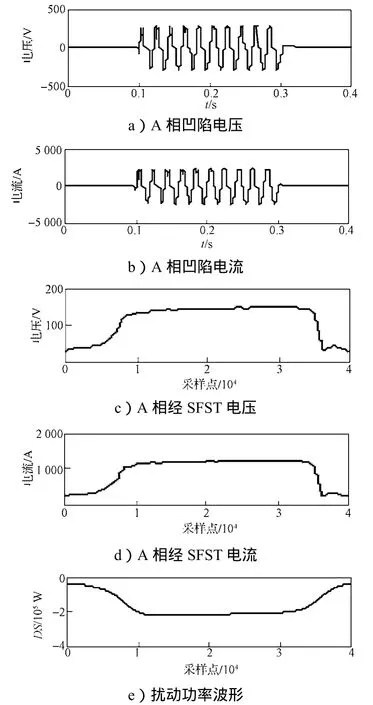
图13 变压器励磁涌流电压M6点凹陷扰动源定位波形图Fig. 13 Voltage sag disturbance source location ofM6caused by inrush exciting current of transformer waveform

从图12中可以看出，M5点处的DS＞0，根据扰动功率定位法判据可知，扰动源发生在M5点的下游；从图13中可以看出，M6点处的DS＜0，因而扰动源位于M6的上游。

3.4 故障自清除引起的电压凹陷扰动源定位

图14所示为故障自清除仿真模型图。仿真系统频率为50 Hz，仿真时间为0.4 s。监测点为M7和M8。故障自清除引起电压凹陷时，监测点M7和M8处的A相凹陷波形、经SFCST的基波电压和电流波形以及扰动功率波形如图15和16所示。

从图15中可以看出，M7点处的DS＞0，根据扰动功率定位法判据可知，扰动源发生在M7点的下游；从图16中可以看出，M8点处的DS＜0，因而扰动源位于M8的上游。

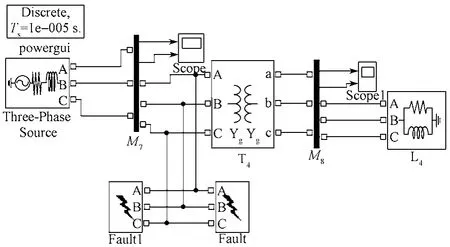
图14 故障自清除仿真模型Fig. 14 A simulation mode of trouble elimination

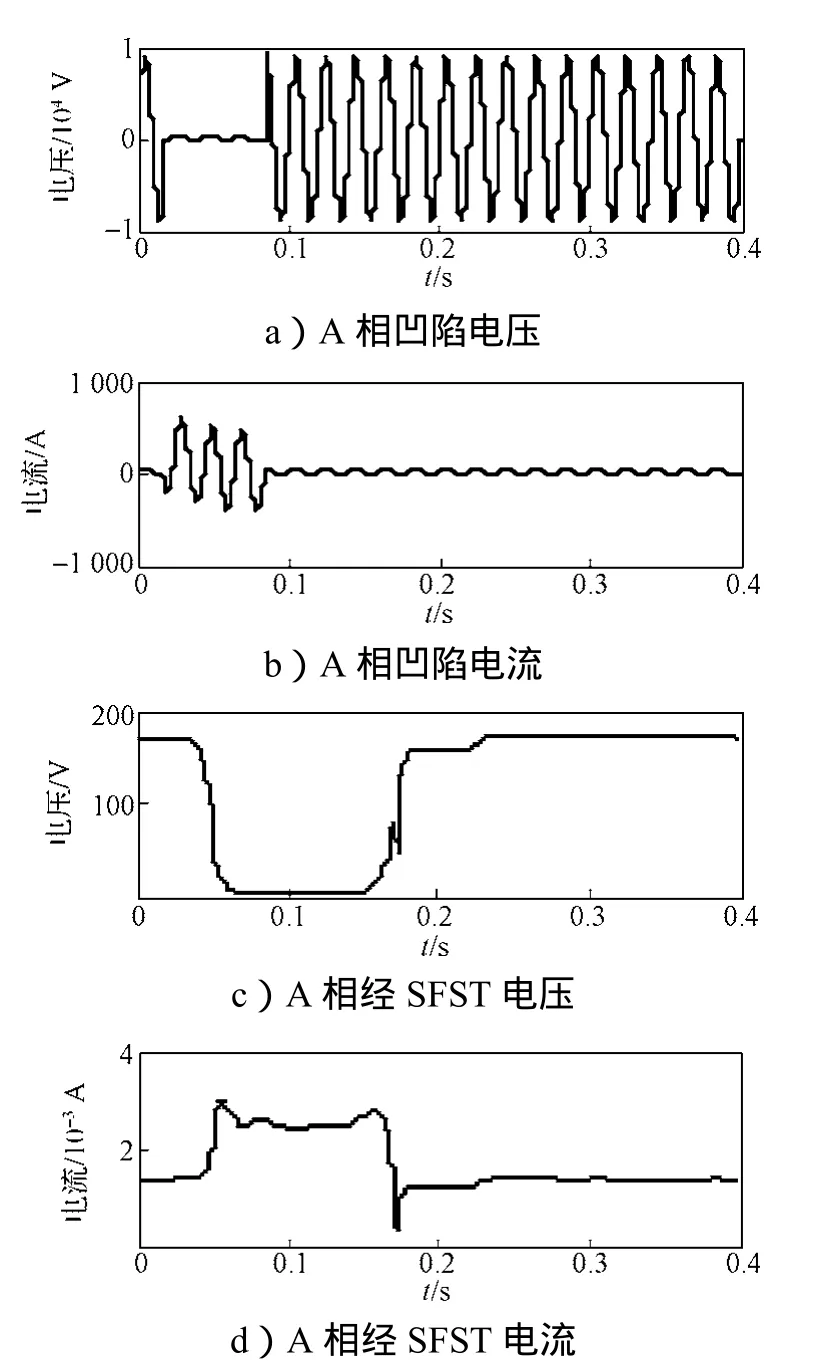
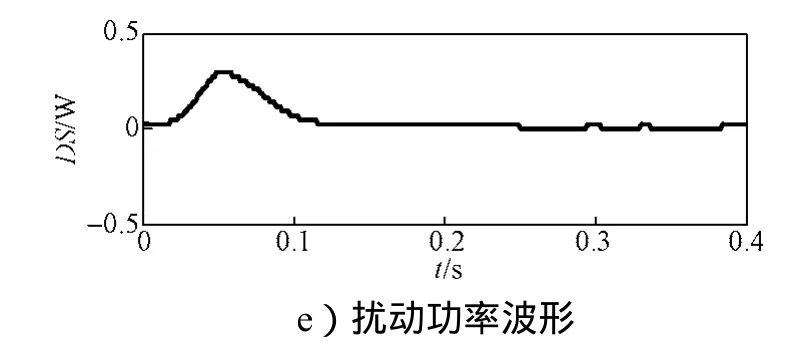
图15 故障自清除引起的M7点电压凹陷扰动源定位波形图Fig. 15 Voltage sag disturbance source location ofM7caused by trouble self-elimination waveform

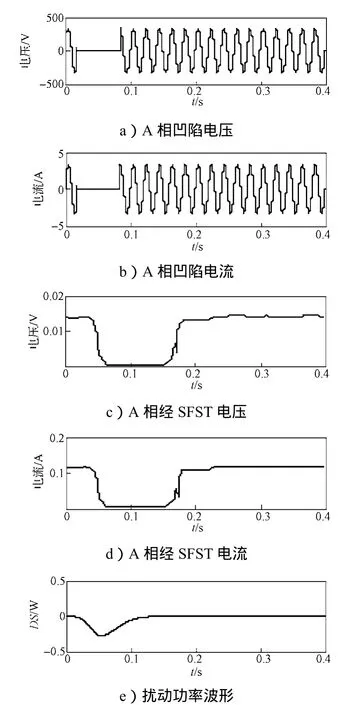
图16 故障自清除引起的M8点电压凹陷扰动源定位波形图Fig. 16 Voltage sag disturbance source location ofM8caused by trouble self-elimination waveform

表1给出了4种仿真模型的8个监测点的扰动功率的极性变化。可知扰动源位于监测点M1、M3、M5、M7的下游，位于监测点M2、M4、M6、M8的上游，从以上结果可看出，本文方法定位扰动源结果与实际情况相符。

表1 8个监测点的电压凹陷源定位结果Table 1 Location results of voltage sag disturbance source of eight monitoring sites

4 结语

本研究采用SFCST来计算瞬时视在功率，直接利用基频电压、电流复向量，经过交叉S变换即可得到瞬时视在功率，进而采用扰动功率法实现电压凹陷扰动源的定位，为扰动源的定位提供了一种新思路。由于单基频S变换相对于S变换只需要计算基波频率向量，因而大大减少了运算量，提高了运算速度，便于实时应用。

通过对由短路故障、异步电动机启动、变压器励磁涌流以及故障自清除引起的4种典型的电压凹陷源进行建模仿真，对8个监测点进行了分析判断，结果验证了该方法的准确性，具有实际应用前景。

[1] 唐 轶，文 雷，于 琪，等. 基于扰动功率的电压暂降源方向判断[J].中国电机工程学报，2015，35(9)：2202.TANG Yi， WEN Lei，YU Qi，et al. A Direction Finder for Voltage Sag Source Based on the Disturbance Power Direction[J]. Proceedings of the CSEE，2015，35(9)：2202.

[2] GOMEZ J C，MORCOS M M.Voltage Sag and Recovery Time in Repetitive Events[J]. IEEE Transactions on Power Delivery，2002，17(4)：1037-1043.

[3] PRADHAN A K，ROUTRAY A. Applying Distance Sign-Based Method for Voltage Sag Source Detection[J].IEEE Transactions on Power Delivery，2005，20(3)：529-531.

[4] 刘颖英，王同勋，冯丹丹，等.基于多重判据的电压暂降故障源定位方法[J]. 中国电机工程学报，2015，35(1)：103-111.LIU Yingying，WANG Tongxun，FENG Dandan，et al. Multiple Criterions Based Voltage Sag Location Method[J]. Proceedings of the CSEE，2015，35(1)：103-111.

[5] PARSONS A C，GRADY W M，POWERS E J，et al. A Direction Finder for Power Quality Disturbances Based Upon Disturbance Power and Energy[J]. IEEE Transactions on Power Delivery，2000，15(3)：1081-1086.

[6] 张文涛，王成山. 基于改进扰动功率和能量法的暂态扰动定位[J].电力系统自动化，2007，31(8)：32-35.ZHANG Wentao，WANG Chengshan. Transient Disturbances Location Based on Improved Disturbance Power and Energy[J]. Automation of Electric Power Systems，2007，31(8)：32-35.

[7] BOLLEN M H J. Voltage Recovery After Unbalanced and Balanced Voltage Dips in Three-Phase Systems[J]. IEEE Power Engineering Review，2002，22(10)：63-64.

[8] STOCKWELL R G，MANSINHA L，LOWE R P. Localization of the Complex Spectrum：TheSTransform[J]. IEEE Transactions on Signal Processing，1996，44(4)：998-1001.

[9] 易吉良，彭建春，李圣清. 电容器投切扰动源的交叉不完全S变换定位方法[J]. 电力系统保护与控制，2012，40(6)：30-34.YI Jiliang，PENG Jianchun，LI Shengqing. Tracking Capacitor Switching Disturbance Source Using Cross Incomplete S-Transform[J]. Power System Protection and Control，2012，40(6)：30-34.

[10] 吕干云，吴育聪. 电压暂降源定位的优化综合判据法[J]. 电力系统保护与控制，2013，41(5)：66-71.LGanyun，WU Yucong. Optimization Comprehensive Criterion for Voltage Sag Source Location[J]. Power System Protection and Control，2013，41(5)：66-71.

[11] 唐 轶，陈 嘉，樊新梅，等. 基于扰动有功电流方向的电压暂降源定位方法[J]. 电工技术学报，2015，30(23)：102-109.TANG Yi，CHEN Jia，FAN Xinmei，et al. A Method for Voltage Sag Sources Based on Disturbance Active Current Direction[J]. Transactions of China Electrotechnical Society，2015，30(23)：102-109.

[12] 程 焰，易吉良，张 帅，等. 基于单基频S变换的电压凹陷分类[J]. 湖南工业大学学报，2016，30(4)：21-26.CHENG Yan，YI Jiliang，ZHANG Shuai，et al. Classification of Voltage Sags Based on Single Fundamental Frequency S-Transform[J]. Journal of Hunan University of Technology，2016，30(4)：21-26.

(责任编辑：廖友媛)

Voltage Sag Source Location Based on Single Fundamental Frequency Cross S-Transform

YANG Xiaofang，YI Jiliang，CHENG Yan，ZHOU Man，LIU Xiaowen
（School of Electrical and Information Engineering，Hunan University of Technology，Zhuzhou Hunan 412007，China）

The precise location of voltage sag disturbance source relative to monitoring site helps to clarify the accountability of the responsibility either by the customers or the suppliers. In order to precisely locate the voltage sag disturbance source, a new location method of disturbance power has been proposed based on single fundamental frequency cross S-transform. First, the voltage and current signals, which are collected by the monitoring sites, are transformed by single fundamental frequency cross S-transform, thus obtaining the fundamental vectors of the voltage and current. Next, with the fundamental vectors of voltage and current transformed by single fundamental frequency cross S-transform, the instantaneous apparent power can be extracted from the model, and the instantaneous apparent disturbance power can be obtained. Finally, locate the source of voltage sag disturbance by adopting the disturbance power criterion. An analysis has been made of the short circuit fault, induction motor starting and transformer inrush current and fault clearance of four typical voltage sag source due to modeling and simulation, as well as the eight monitoring points, which result verifying the accuracy and effectiveness of the proposed method.

single fundamental frequency cross S-transform；disturbance power；voltage sag；location

TM714

：A

：1673-9833(2017)03-0040-08

10.3969/j.issn.1673-9833.2017.03.007

2016-12-20

国家自然科学基金资助项目（61503131），湖南省教育厅科学研究基金资助项目（14C0327）

杨晓芳（1991-），女，山西阳泉人，湖南工业大学硕士生，主要研究方向为电能质量分析，E-mail：3098192146@qq.com

易吉良（1972-），男，湖南株洲人，湖南工业大学副教授，主要从事电能质量分析，数字信号处理方面的教学与研究，E-mail：yi.jiliang@163.com