正交优化法在区域供冷系统管网优化设计中的应用

谭超毅，刘少杰，胡海华，张 超

（1.湖南工业大学 建筑节能与环境控制关键技术协同创新中心，湖南 株洲 412007；2. 深圳达实智能股份有限公司 数据中心事业部，广东 深圳 518057；3.株洲市住房与城乡建设局 建筑节能科，湖南 株洲 412007）

正交优化法在区域供冷系统管网优化设计中的应用

谭超毅1，刘少杰1，胡海华2，张 超3

（1.湖南工业大学 建筑节能与环境控制关键技术协同创新中心，湖南 株洲 412007；2. 深圳达实智能股份有限公司 数据中心事业部，广东 深圳 518057；3.株洲市住房与城乡建设局 建筑节能科，湖南 株洲 412007）

以管网年折算总费用最低为目标，选取管径、冷水流速、管道保温层厚度作为优化变量，将用户冷负荷需求和合理冷水流速范围作为约束条件，建立区域供冷系统管网优化目标函数，并采用正交优化方法进行优化计算。以株洲市神农城区域供冷管网为例进行计算，结果表明：管网设计参数对管网经济性的影响排序依次为：d（管径）、v（流速）、δt（保温层厚度），且三者都是不可忽视的主要因素；株洲市神农城区域供冷系统管网优化设计参数组合为de=300 mm，ve=1.06 m/s，δte=0.057 m，年折算总费用为282 729元；正交优化法可以作为区域供冷系统管网优化设计的工具，适合一般工程技术人员使用。

正交优化法；区域供冷系统；管网优化设计；年折算总费用

Keywords：orthogonal optimization；district cooling system；pipe network optimization design；reducedannual total cost

0 引言

区域供冷系统由供冷基站、输配管网和用户入口装置3个部分组成，是一种以满足特定区域内一个或多个建筑物的空调冷源需求为目的，由专门的供冷基站集中制备冷水，并通过输配管网将冷水输送给用户的新型冷源供应系统[1]。设计合理的区域供冷系统具有节能、节资、环保的巨大优势。我国已经建成且影响较大的区域供冷项目有：北京中关村、上海世博园、广州大学城、南京鼓楼高新技术产业园区、武汉金融港产业园及大连星海湾商务区等。

区域供冷系统相对单体建筑集中式冷源供应系统，增加了室外管网，具有供回水流量大、管径大及冷量损失大，初投资和运行费用较高等特征。要解决上述问题，必须对区域供冷系统管网进行优化设计。我国广大科研工作者针对区域供冷系统的管网布置、供冷半径、管径、管道保温层厚度、供回水温差等问题进行了较为全面的研究，得出了许多有价值的研究成果。如冯小平[2]以上海世博园区域供冷系统为背景，建立以管网寿命周期内费用最小，满足系统技术要求的优化模型，进行管径和管网布置优化。夏博[3]以管网经济性最优为目标建立管网优化模型，以确定管径、供回水温差、供冷长度等参数。舒海文[4]以管网节能性最好为目标，建立管网优化模型来确定管径。这些研究需要编制复杂程序或依赖复杂的软件，不适合一般工程技术人员日常使用。

正交优化设计与统计分析计算的方法（简称正交优化法），通过利用正交表进行多因素优化试验和设计，并对试验结果进行统计分析计算，得到优化结果，具有通俗易懂、简单方便的特点。例如：陈磊等[5]将正交多智能体算法应用于求解直接优化调度模型；戴乾生等[6]将正交试验设计应用于管道扩建优化设计；张新平等[7]将正交表应用于管网布置优化。但是，还未见将正交优化法运用于区域供冷系统管网优化设计的报道。因此，本文将以株洲市神农城区域供冷系统管网优化设计为例，阐述如何应用正交优化法对区域供冷系统管网进行优化设计。

1 区域供冷系统管网优化设计模型

1.1 目标函数

区域供冷系统管网年折算总费用由管网初投资年折算费用、管网折旧和维修年均费用、变频水泵初投资年折算费用、水泵年运行费用和管网冷量损失年费用5个部分构成，即目标函数为

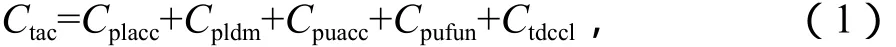
式中：Ctac为管网年折算总费用，元；

Cplacc为管网初投资年折算费用，元；

Cpldm为管网折旧和维修年均费用，元；

Cpuacc为水泵初投资年折算费用，元；

Cpufun为水泵年运行费用，元；

Ctdccl为管网冷量损失年费用，元。

1.2 约束条件

1）用户冷负荷需求

对于一个用户确定的区域供冷系统，冷负荷是一常量。因此，用户冷负荷就成为进行区域供冷系统管网优化的一个基本约束条件。

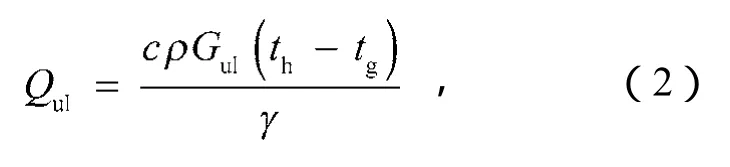
式中：Qul为用户冷负荷，W；

c为冷水定压比热容，取4 187 J/(kg·℃）；

ρ为冷水密度，kg/m³；

Gul为用户所需的冷水体积流量，m³/s；

tg,th分别为冷水供、回水温度，℃；

γ为冷水温度备用系数，取1.3[8]。

2）流速范围

文献[9]中的相关条文规定：区域供冷系统管网设计的最大冷水流速度不应超过2.9 m/s，但考虑系统实际负荷率和动能损耗等方面的影响，可将其上限扩大至3.5 m/s，由此可得

式中vi为第i管段的冷水流速，m/s。

1.3 优化设计模型

综合式（1）～（3），可得区域供冷系统管网优化设计模型为

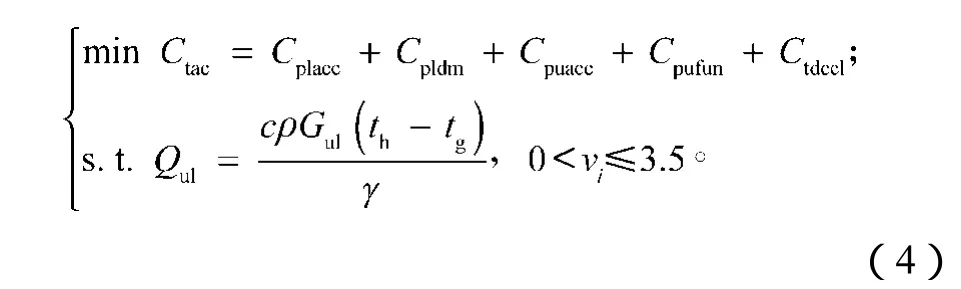
2 管网设计参数与正交表设计

采用区域供冷系统管网优化设计模型（4）来获得最佳的设计参数，理论上可以通过对目标函数求偏导数再解方程来获得，但式（4）是超越方程，无法通过求偏导数再解方程来获得。另外，若通过绘制目标函数的曲线来获取最佳参数，由于设计参数多，且是变量，作图将非常复杂，显然也不容易获取最佳设计参数。

用正交表来优化设计参数，能够发挥正交表的3个优势：

1）计算次数少，统计分析简单，在所有可能的试验方案中可均匀地挑选出具有较强代表性的少数试验方案；

2）通过将挑选出来的少数试验方案的试验结果进行统计与分析，推出较优的方案，而且所得到的优选方案往往不包括在这些少数试验方案中，具有一定的拓展性；

3）对试验结果作进一步分析，可以得到试验结果之外的更多信息，如某个试验因素对试验结果影响的重要程度、各因素对试验结果的影响趋势等。

2.1 参数及变化范围与正交表中因素及水平之间的关系

用正交表对管网设计参数进行优化，需把管网的设计参数对应正交表的因素，管网设计参数的变化范围对应正交表水平数的取值范围。同时，应注意现有正交表的水平数及因素数都是有限的，为了有效利用现有正交表并且减少计算量，要尽量减少因素数和水平数。

2.2 参数的并归整合

管网设计参数越多，优化难度越大，所以优化的准确度也会随之下降。优化模型（4）中的目标函数由管网初投资年折算费用、管网折旧和维修年均费用、水泵初投资年折算费用、水泵年运行费用、管网冷量损失年费用5部分组成，且都与管径有关，后2项还与流速有关。且虽然保温层厚度也与管径有关，但它们的变化不是一个数量级，因此宜单独设置。因此，优化模型（4）中的变量可以并归整合为管径、流速和保温层厚度3个独立的变量。

2.3 正交表设计

1）正交表因素的确定。正交表的因素数和水平数越多，计算越复杂，计算难度也越大；同时，因数和水平数也受制于已有的正交表；然而，因素水平数太少，也不能满足工程优化的需要。因此，一般取因素数3～5个为宜。

2）因素水平数的确定。因素水平数应根据已有的正交表来确定，一般重要的因素可多取一些水平；各水平的数值应适当拉开，有利于对试验结果的分析。对于具体的工程项目，往往用约束条件和设计规范推荐的值来进行计算初始水平和最终水平。对于供冷管网，是以供冷量这个约束条件和设计规范规定的流速推荐值，来计算并确定管径的初始水平和最终水平的。

3 算例分析

湖南省株洲市神农城区域供冷系统采用的是分区二级泵系统，制冷站至酒店用户入口的单程管道长度为519.7 m，则供回水管道的总长度为1 039.4 m，酒店总冷负荷为1 011 kW。按规范推荐值，流速下限取0.5 m/s，上限取2.9 m/s，得出管道的直径下限为150 mm，上限为400 mm。将该项目的基本参数代入式（4）中，并参考文献[8]可得该供冷系统管网优化设计模型为

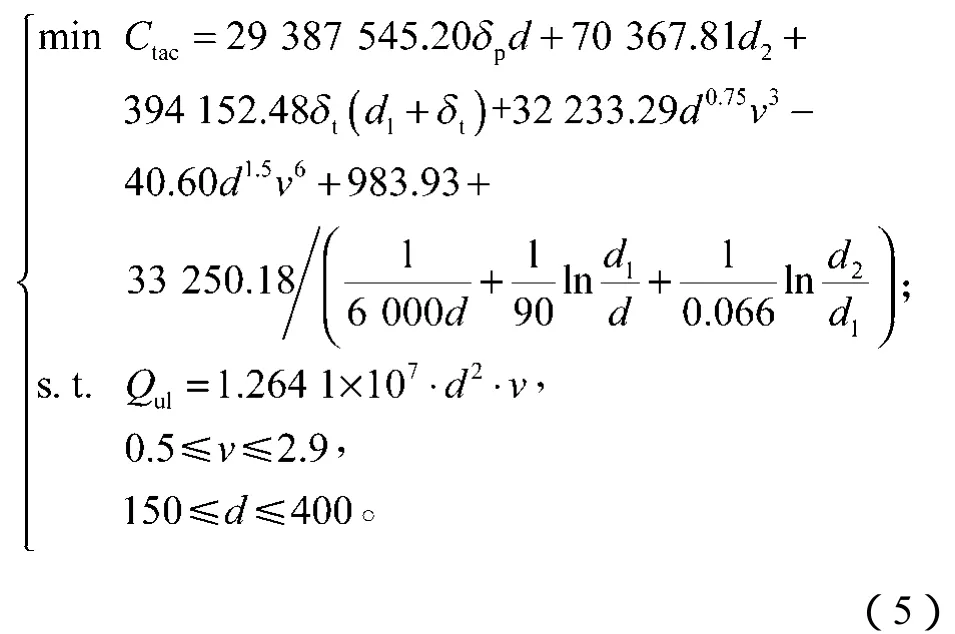
式中：v为管内水流速，m/s；

d为管径，mm；

d1为管外径，mm；

d2为保温后管外径，mm；

δp为管道厚度，mm；

δt为保温层厚度，mm。

式（5）中的量满足：

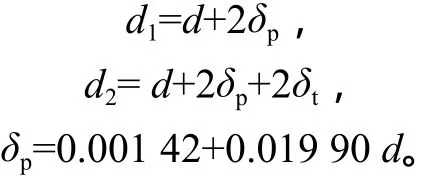
由式（5）可知，Ctac=f(d,v,δt)，且实际优化设计模型的约束条件相对通用优化设计模型（4）更加严格。可见，目标函数是一个单指标、三因素的函数，用编程计算或其它工具进行优化计算，不适合一般的工程技术人员使用，宜采用正交优化法对它进行优化计算。

按约束条件和标准管径条件及文献[10]中关于保温层厚度的规定，将管径的水平定为 200, 250, 300,350, 400 mm；冷水流速的水平定为1.0, 1.5, 2.0, 2.5,2.9 m/s；管道保温层厚度的水平定为0.045, 0.049,0.053, 0.057, 0.061 m。可见，在此应选择一个适合3因素5水平的正交表进行优化计算。

1）确定因素水平表。为避免人为因素导致的系统误差，应该按照“随机化”的方法确定因素水平表。本文采用抽签的方法随机确定，最后得到第一次正交优化计算时的因素水平表如表1所示。

2）计算方案及结果分析。本次计算的因素有3个，且每个因素都有5个水平，不考虑因素间的交互作用，选取正交表L25(56)来进行正交优化计算。正交表的每一行对应着一个计算方案，计算方案与结果分析如表2所示。

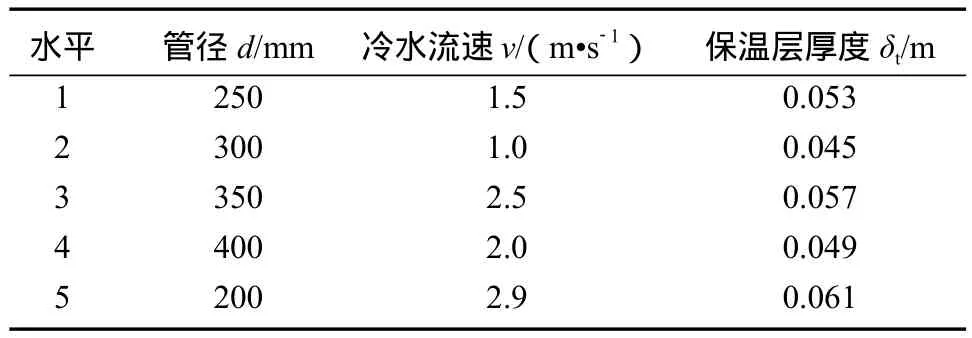
表1 第一次正交优化计算时的因素水平表Table 1 Factor level of the fi rst orthogonal optimization calculation

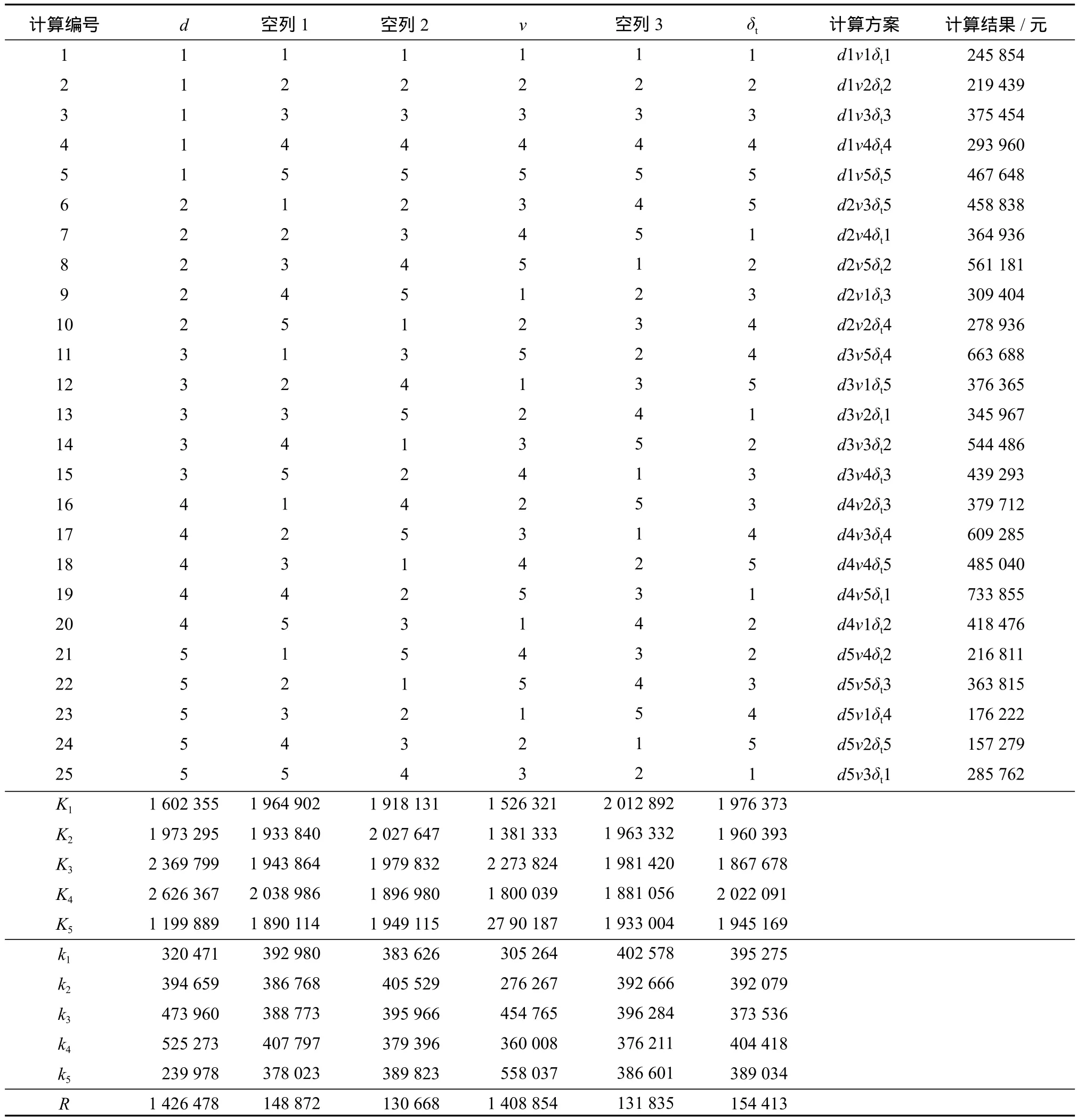
表2 第一次正交优化计算时的计算方案及结果分析Table 2 Calculation scheme and result analysis of the fi rst orthogonal optimization calculation

由表2中各列的极差值可知，Rd＞Rv＞Rδt，并且Rd,Rv远大于Rδt。结果表明：各管网设计参数对管网经济性的影响从主到次的顺序依次为：d（管径）、v（流速）、δt（保温层厚度）；管径d和流速v对于管网经济性的影响远超过保温层厚度δt。

空白列的极差都比因素列小，这说明参数间不存在交互作用或者是漏掉某一设计参数的可能性，该正交优化设计是合理的。

由各列中的Ki或ki的值可知，d列：K5＜K1＜K2＜K3＜K4，v列：K2＜K1＜K4＜K3＜K5，δt列：K3＜K5＜K2＜K1＜K4。可见，理论计算分析得到的最优组合方案是d5v2δt3，即管径d为200 mm、流速v为1.0 m/s、保温层厚度δt为0.057 m。此组合方案不在原定试验计算方案中，说明正交优化可以得到实验或计算以外的最佳组合方案。由表中的计算结果可知其经济性最好的方案是d5v2δt5，即管径d为200 mm、流速v为1.0 m/s、保温层厚度δt为0.061 m。经计算，方案d2v2δt3的经济性好于方案d5v2δt5；所以，可能的最优组合方案应该是d5v2δt3，无需进行下一步的正交优化计算。

按照文献[11]中规定的管网主干线平均比摩阻值进行检查：当主干线供回水管的总长度时，平均比摩阻值应在30～60 Pa/m范围内，检查计算此组合方案d2v5δt3的比摩阻值达到了69.8 Pa/m，并且不满足用户负荷需求的约束条件，显然不符合要求。为此，需要根据正交优化趋势图（见图1）进一步分析。

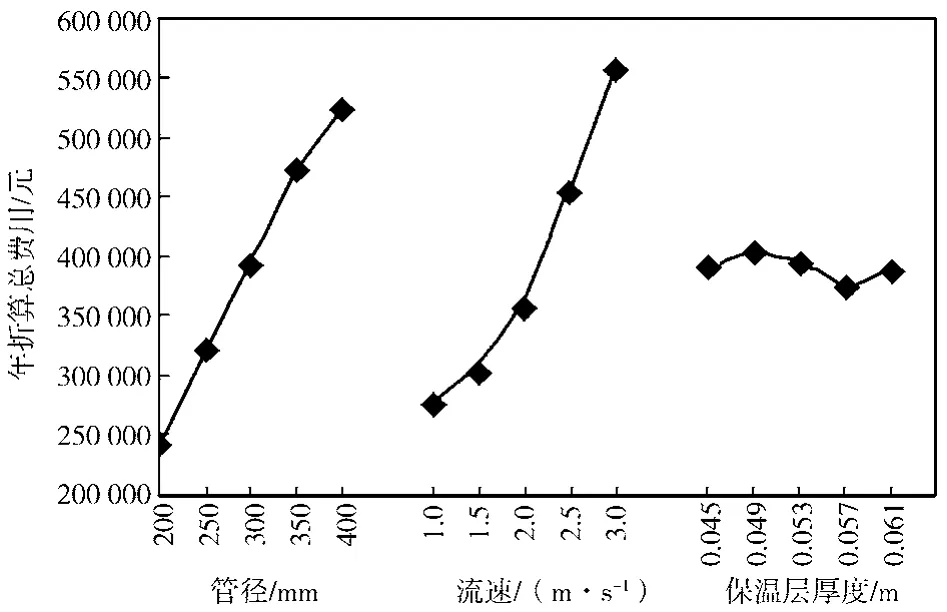
图1 正交优化计算时年折算总费用随因素变化的趋势Fig. 1 Orthogonal optimization calclations with the variaion of the trend of annual total cost factors optimization calculation

由图1可以得知：1）管网年折算总费用随管径的增大而快速增大，增长速度是三因素中最大的；2）流速越大，管网年折算总费用越大；3）保温层厚度对管网年折算总费用的影响呈微波浪形变化，在0.057 m处时费用最低。这说明，为在满足各约束条件的同时使供冷管网经济性最优，需要经过试算去寻找一个管径、流速尽可能小，保温层厚度为0.057 m的优化设计参数组合。经过试算，得知当管径为300 mm，流速为1.06 m/s时，比摩阻值为46.49 Pa/m，管网年折算总费用最低，即为282 729元。因此，确定该管网优化设计参数如下：de=300 mm，ve=1.06 m/s，δte=0.057 m。

4 结论

以管网年折算总费用最低为目标，用户冷负荷需求、冷水流速范围为约束条件，建立了区域供冷管网系统优化设计模型，其优化设计参数可合并归整为管径d、流速v、保温层厚度δt三个参数。

在对供回水管道总长度为1 039.4 m，用户总冷负荷为1 011 kW的管网正交优化设计计算与分析中，管网设计参数对管网经济性的影响程度排序依次为：d（管径）＞v（流速）＞δt（保温层厚度），且三者都是不可忽视的主要影响因素。同时，管网优化设计参数组合应为：de=300 mm，ve=1.06 m/s，δte=0.057 m，此条件下管网年折算总费用为282 729元。

正交优化法具有计算简便、计算结果较可靠，拓展性较强的特点，可以作为区域供冷系统管网优化的工具，适合一般工程技术人员掌握和使用。

[1] 李著萱，贺继超，吕访桐，等. 区域供冷与余热利用的优势与风险研究[J]. 暖通空调，2013，43(2)：2-5.LI Zhuxuan，HE Jichao，LÜ Fangtong，et al.Superiority and Risk of District Cooling and Excess Heat Utilization[J]. Journal of HV and AC，2013，43(2)：2-5.

[2] 冯小平. 上海世博园区域供冷系统管网优化设计研究[D]. 上海：同济大学，2007.FENG Xiaoping. Study on Optimal Design of District Cooling System Pipe Network in Shanghai EXPO[D].Shanghai：Tongji University，2007.

[3] 夏 博. 区域供冷系统供冷面积及最远输送距离研究[D]. 长沙：湖南大学，2014.XIA Bo. The Research of Economy Cooling Area and the Maximum Conveying Distance in District Cooling System[D]. Changsha：Hunan University，2014.

[4] 舒海文. 热泵区域供热（冷）系统的节能优化与评价[D].大连：大连理工大学，2012.SHU Haiwen. Energy-Saving Evaluation and Optimizationof Heat Pump District Heating and Cooling System[D].Dalian：Dalian University of Technology，2012.

[5] 陈 磊，张土桥. 正交多智能体算法求解管网直接优化调度模型[J]. 哈尔滨工业大学学报，2008，40(4) ：644-649.CHEN Lei，ZHANG Tuqiao. An Orthogonal Multi-Agent Algorithm for Solving the Direct Optimal Operation Model of Water Distribution Network[J]. Journal of Harbin Institute of Technology，2008，40(4)：644-649.

[6] 戴乾生，汪玉春，殷 平. 正交试验设计在管道扩建优化设计中的应用[J]. 天然气工业，2011，31(8)：90-93.DAI Qiansheng，WANG Yuchun，YIN Ping. Application of Orthogonal Design in an Optimal Pipeline Extension Project[J]. Natural Gas Industry，2011，31(8)：90-93.

[7] 张新平，林性粹. 正交表优化管网布置的原理[J]. 上海农学院学报，1993，12(1)：20-24.ZHANG Xinping，LIN Xingcui. The Principle of Optimal Layout for Irrigation Pipe-Network by the Orthogonal Table Method[J]. Journal of Shanghai Agricultural College，1993，12(1)：20-24.

[8] 刘金平，杜艳国，陈志勤. 区域供冷系统中冷冻水输送管线的优化设计[J]. 华南理工大学学报（自然科学版），2004，32(10)：28-31.LIU Jinping，DU Yanguo，CHEN Zhiqin. Optimized Design of the Chilled Water-Conveying Pipeline in the District Cooling System[J]. Journal of South China University of Technology(Natural Science Edition)，2004，32(10)：28-31.

[9] 中国建筑科学研究院. 民用建筑供暖通风与空气调节设计规范：GB 50736—2012[S]. 北京：中国建筑工业出版社，2012：141.China Academy of Building Research. Design Code for Heating Ventilation and Air-Conditioning of Civil Buildings：GB 50736—2012[S]. Beijing：China Architecture and Building Press，2012：141.

[10] 中国建筑科学研究院. 公共建筑节能设计标准：GB 50189—2015[S]. 北京：中国建筑工业出版社，2015：55.China Academy of Building Research. A Design Standard for Energy Ef fi ciency of Public Buildings：GB 50189—2015[S]. Beijing：China Architecture and Building Press，2015：55.

[11] 住房和城乡建设部工程质量安全监管局，中国建筑标准设计研究院. 全国民用建筑工程设计技术措施：暖通空调•动力[M]. 北京：中国计划出版社，2009：50.Department of Construction Engineering Quality &Safety Supervision Ministry of Housing and Urban-Rural Development of the P. R. China，China Institute of Building Standard Design & Research. National Technical Measures for Design of Civil Construction-HV and AC[M]. Beijing：China Planning Press，2009：50.

（责任编辑：邓光辉）

Application of Orthogonal Optimization Method in an Optimal Design of Pipe Network in the District Cooling System

TAN Chaoyi1， LIU Shaojie1，HU Haihua2，ZHANG Chao3
（1. Collaborative Innovation Center for Key Technologies of the Building Energy Conservation and Environment Control，Hunan University of Technology，Zhuzhou Hunan 412007，China；2. Data Center Division，Shenzhen Das Intellitech Co., Ltd.，Shenzhen Guangdong 518057，China；3. Building Energy Conservation Section，Zhuzhou Construction Bureau of Housing and Urban，Zhuzhou Hunan 412007，China）

With the minimum total cost of pipe network taken as the goal, the pipe diameter, the cold water fl ow rate and the thickness of the pipe insulation layer taken as the optimization variables, the user cooling load demand and the reasonable cold water flow velocity range taken as the constraint conditions, an effort has been made to establish the objective function of the pipe network optimization of the district cooling system, with the orthogonal optimization method adopted to optimize the calculation. The results show that: arranged in a descending order, the in fl uence of design parameterson the economical ef fi ciencyof the pipe network will be:d(pipe diameter),v(velocity),δt(thermal insulation layer thickness), with all the three factors being fundamentally indispensable; the optimal design parameters of the district cooling system in Zhuzhou Shennong Urban District will be:de= 300 mm,ve= 1.06 m/s,δte= 0.057 m, with its annual total cost being 282 729 yuan; the orthogonal optimization method, which can be used as an optimization tool for the optimal design of pipe network in the district cooling system, proves to be useful and helpful for the general engineers and technicians.

TU831.3+7

：A

：1673-9833(2017)03-0026-06

10.3969/j.issn.1673-9833.2017.03.005

2016-12-19

国家科技支撑计划课题基金资助项目（2011BAJ03B07）

谭超毅（1956-），男，湖南株洲人，湖南工业大学教授，主要从事建筑设备节能技术方面的教学与研究，E-mail：tanchaoyi123@126.com

刘少杰（1992-），男，湖南衡阳人，湖南工业大学硕士生，主要研究方向为建筑设备节能技术，E-mail：981305827@qq.com