挠性陀螺寻北仪解算方法研究

贾智学 张小凯 任佳婧

中国航天科技集团公司第九研究院七一Ο七厂 ，宝鸡721006



挠性陀螺寻北仪解算方法研究

贾智学 张小凯 任佳婧

中国航天科技集团公司第九研究院七一Ο七厂 ，宝鸡721006

研究了挠性寻北仪解算算法，首先介绍了寻北仪的组成和算法原理，在此基础上建立了陀螺和加速度计的误差模型。根据二位置寻北方法，分别推导了寻北系统在基座水平和倾斜情况下的寻北算法，试验表明该算法能满足中低寻北精度要求。

挠性陀螺仪；寻北仪；寻北技术方案；误差模型；实验

陀螺寻北仪是一种精密惯性测量仪器[1], 通常用于为火炮、侦察车辆和地面雷达等机动武器系统提供方位参考。近年来，寻北仪在国防军事高科技领域的需求越来越迫切，同时在民用工程中也越来越显示出广阔的应用前景。

寻北技术目前常用技术途径主要包括天文观测法、地磁寻北法[2]和惯性寻北法[3]，其中陀螺寻北仪相对其他方式具有独特的优点，寻北测量不受天气、地磁场等外界环境的影响。它利用陀螺仪原理测量地球自转角速率在当地水平面投影方向(即真北方位) 的一种惯性测量系统[4]。挠性陀螺的发展已经非常成熟，相对其他种类陀螺具有精度高、体积小、价格便宜等优点，所以挠性陀螺寻北仪是一种性价比很高的寻北系统。本文针对双轴挠性陀螺仪的优点，主要进行了二位置寻北技术的研究。

1 寻北仪组成及测量原理

1.1 寻北仪组成

寻北仪主要由高精度动力调谐陀螺仪、石英加速度计、陀螺再平衡电路、数据采集电路、信号处理电路、二次电源、显示装置、解算软件和机械转动装置构成,其系统组成框图如图1所示。

图1 系统组成框图

1.2 寻北仪测量原理

寻北仪测量原理是利用陀螺敏感地球的自转角速度，通过解算得到载体某一固定轴与真北方向的夹角即方位角。加速度计敏感地球重力加速度，从而得到载体的俯仰角与滚动角，用于倾斜状态方位解算。陀螺寻北仪寻北方式可以分为连续转动方案、多位置方案[5]和两位置方案等。其中，两位置寻北方案由于其寻北时间短，易于实现而得到广泛应用。陀螺数学模型如式(1)和(2)，加速度计数学模型如式(3)和(4)所示:

UgxKgx=Dx0+DxxAx+DxyAy+DxzAz+ωecosLsinφ

(1)

UgyKgy=Dy0+DyxAx+DyyAy+DyzAz+ωecosLcosφ

(2)

UaxKay=Kax0+Aax

(3)

UayKaz=Kay0+Aay

(4)

式(1)和(2)中，Ugx和Ugy为陀螺仪输出；Kgx和Kgy为陀螺仪标度因数；ωe为地球自转角速度率；Ax,Ay,Az为三轴的加速度；L为当地地理纬度；φ为与真北方向夹角；Dx0，Dy0为陀螺仪的常值漂移；Dxx，Dxy，Dxz，Dyx，Dyy，Dyz，Dzx，Dzy，Dzz为陀螺仪与加速度一次方有关的误差系数。式(3)和(4)中,Uax和Uay为加速度输出；Kax和Kay为加速度计的标度因数；Kax0和Kay0为加速度计零偏。

2 寻北技术方案

2.1 坐标系的定义与转换关系

惯性坐标系用来表示惯性空间的坐标系

OXiYiZi,导航坐标系为OXnYnZn，Xn轴与Yn轴在当地水平面内，Xn轴与正东方向重合，Yn轴与正北方向重合，Zn轴沿地垂线指天，因此也称为东北天坐标系，如图2所示。

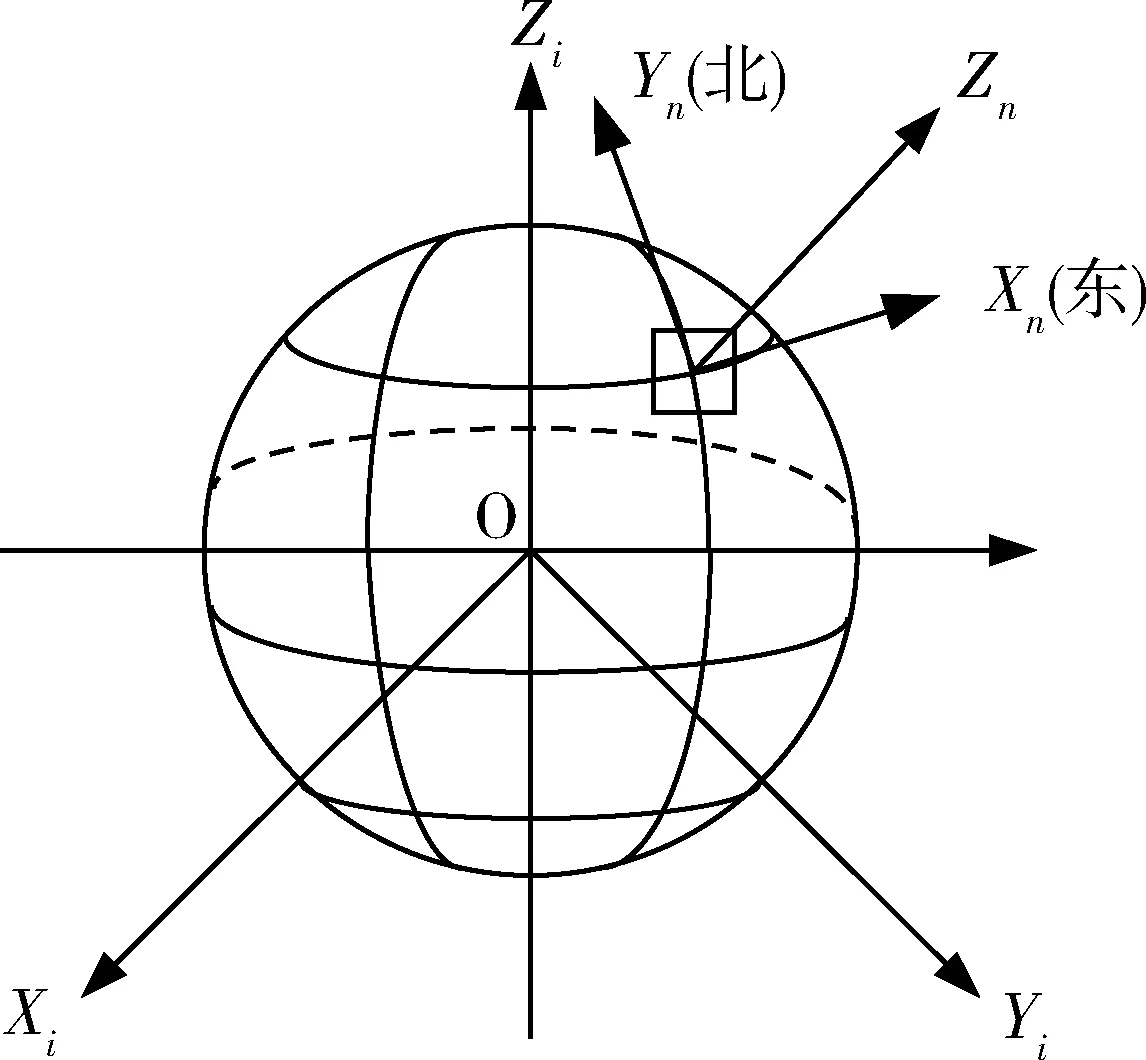
图2 惯性坐标系

载体坐标系OXbYbZb与载体固联，其原点就是载体的重心，Yb轴指向载体的纵轴方向，Xb轴指向载体的右侧，Zb轴与Xb轴和Yb轴构成右手坐标系。

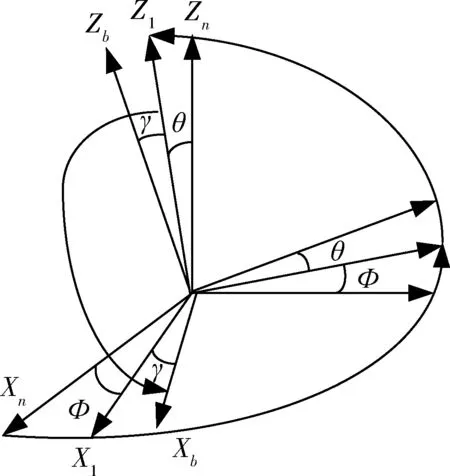
图3 坐标转换图

取东北天为导航坐标系,用OXnYnZn表示；载体坐标系用OXbYbZb表示。首先以OXnYnZn绕OZn轴转动角度Φ，然后绕OX1轴转动角度θ，最后绕OYb轴转动角度γ至载体坐标系OXbYbZb。坐标转换如图3所示。

从导航坐标系OXnYnZn到载体坐标系OXbYbZb转换矩阵如下：

(5)

地球自转角速度在导航坐标系上的投影

(6)

地球自转角速度在载体坐标系上的投影

(7)

重力加速度在导航坐标系上的投影

(8)

重力加速度在载体坐标系上的投影

(9)

2.2 在基座调平状态下寻北

寻北方案按工作状态分为调平状态下寻北和倾斜状态下寻北。两位置寻北时间较短，精度较好，因此广泛采用两位置寻北。 采用两位置寻北方案，根据陀螺的误差模型，将寻北仪转到0°和180°位置时，陀螺仪输出数据之差可以消除陀螺常值误差和与Z向加速度有关的漂移，并对与X向和Y向加速度有关的漂移进行补偿后，计算出地球自转角速度在载体座标系上的投影。

陀螺和加速度计安装方式见图4，陀螺X轴敏感东向角速度，Y轴敏感北向角速度。在水平状态下，X轴和Y轴加速度计输出为0。

图4 陀螺和加速度计安装方式图

根据陀螺仪的输出误差模型，0°位置陀螺输出为

Ugx0Kgx=Dx0+ωecosLsinφ

(10)

Ugy0Kgy=Dy0+ωecosLcosφ

(11)

180°位置陀螺输出为

Ugx1Kgx=Dx 0+ωecosLsin(180+φ)

(12)

Ugy1Kgy=Dy 0+ωecosLcos(180+φ)

(13)

根据式(10)～(13)计算出与真北方向夹角φ为

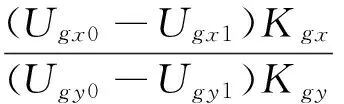
(14)

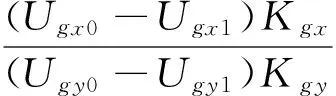
1)arctanΦ≥0，φ1>0，φ=φ1；

2)arctanΦ≥0，φ1<0，φ=90°-φ1；

3)arctanΦ≤0，φ1>0，φ=φ1+180°；

4)arctanΦ≤0，φ1>0，φ=360°-φ1。

2.3 在基座倾斜状态下寻北

当基座处于倾斜状态下，X轴和Y轴加速度计输出不为0，与加速度有关误差系数需要补偿，才能提高寻北精度。当基座在倾斜状态下时，0°位置陀螺仪输出为：

Ugx0Kgx=Dx0+DxxAx+DxyAy+DxzAz+ωbx

(15)

Ugy0Kgy=Dy0+DyxAx+DyyAy+DyzAz+ωby

(16)

180°位置陀螺仪输出为

Ugx1Kgx=Dx0-DxxAx-DxyAy+DxzAz-ωbx

(17)

Ugy1Kgy=Dy0-DyxAx-DyyAy+DyzAz-ωby

(18)

由式(16)和(18)相减，计算出地球自转角速度在载体座标系东向角速度投影：

(19)

由式(17)和(19)相减，计算出地球自转角速度在载体座标系北向角速度投影：

(20)

由式(9)计算出俯仰角和横滚角

(21)

θ=-arcsin(AYb/g)

(22)

γ=arcsin(AXb/gcosθ)

(23)

由式(5)～(7)和式(19)～(20)计算出方位角Ф为

(24)

计算后按照基座调平状态的数据处理方法即可得到φ。

式(24)中，ωbx是地球自转角速度在载体座标系东向投影；ωby是地球自转角速度在载体座标系北向投影；θ是载体横滚角,γ是俯仰角；ωe是地球自转角速度(15.041(°)/h)；L是当地地理纬度。

3 试验验证

3.1 在基座调平状态下寻北实验

在常温状态下，使转台水平，将寻北仪安装在转台上，分别在20°,70°,150°,270°位置进行寻北实验，试验数据如表1所示。

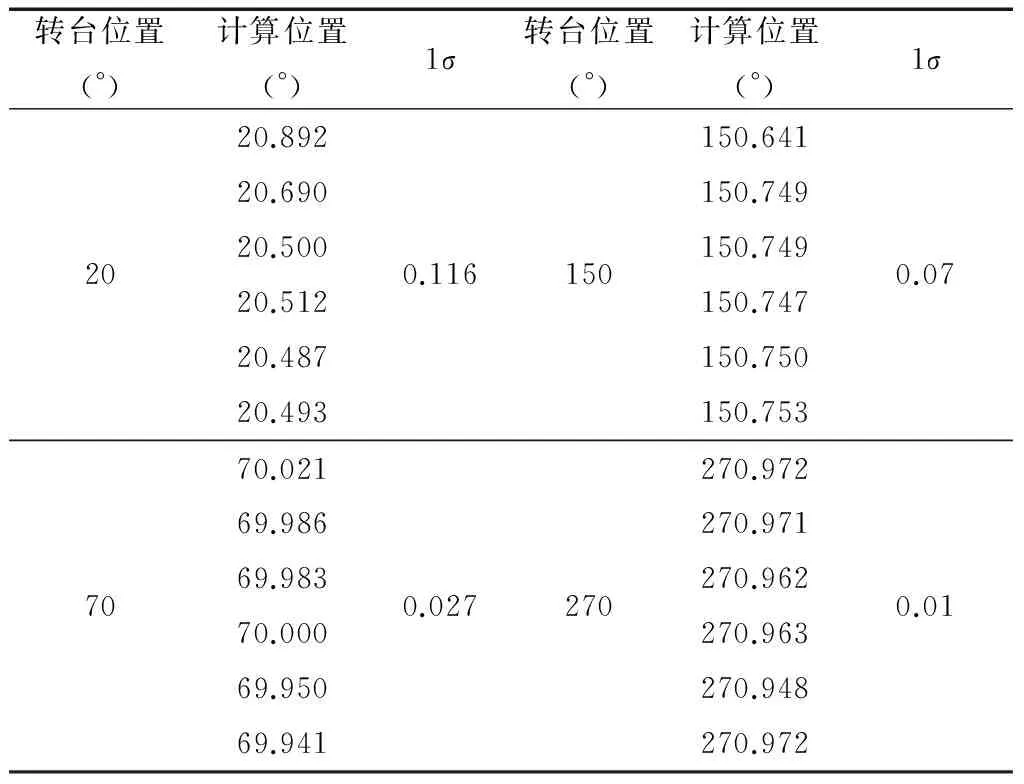
表1 基座调平状态下陀螺实验数据

3.2 在基座倾斜状态下寻北实验

寻北仪在实际工作中不一定是完全水平状态，可能存在一个小角度的倾斜，所以寻北仪的倾斜寻北实验非常必要。实验在-5°倾斜状态下，分别在0°,45°,90°,150° 位置进行，实验数据如表2所示。试验时将寻北装置安装在转台上，利用式(24)解算出寻北结果以及1σ值。

由实验数据可以看出，在倾斜状态下，寻北系统能正确解算出位置信息，实验验证了本文提出的倾斜状态下寻北算法的正确性。

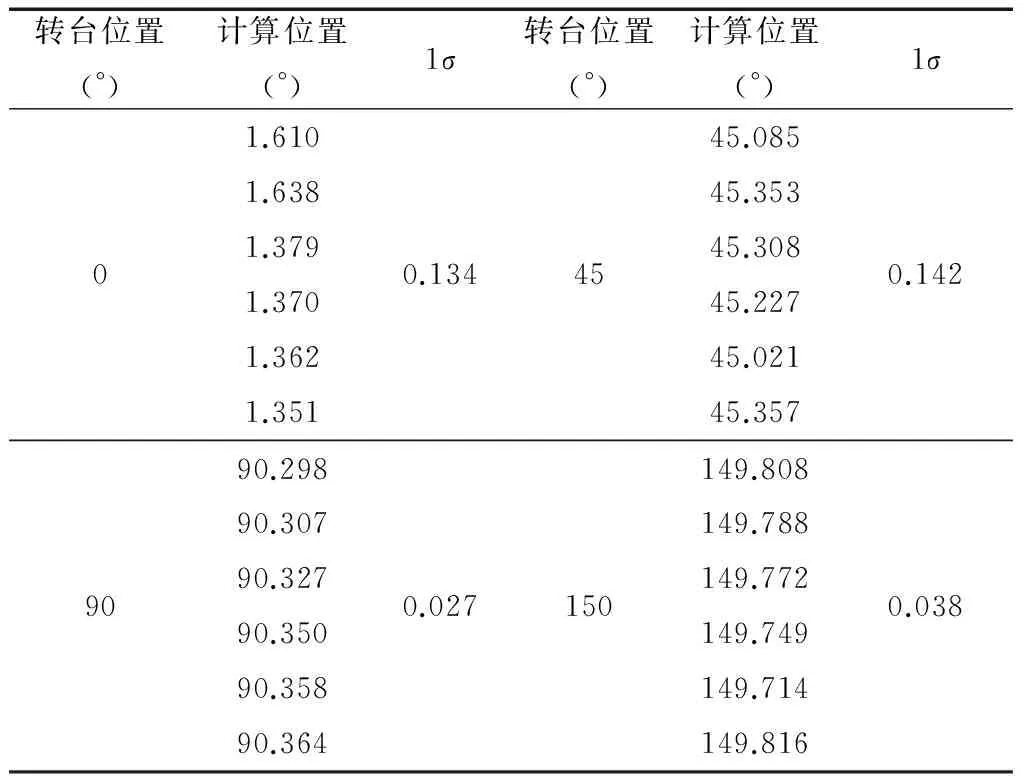
表2 倾斜状态下的寻北数据

4 结论

首先阐述了挠性陀螺寻北仪的基本原理，给出了挠性陀螺寻北仪的数学模型，在此基础上详细讨论了基座处于调平状态和倾斜状态2种情况下的解算算法，试验结果证明，文中建立的数学模型、寻北仪解算方法均能满足中低精度寻北要求。

[1] 白云超，李学琴，马小辉，田育民. 采用旋转调制技术的高精度寻北方案[J]. 中国惯性技术学报，2010，18(4)：421-424.( Bai Yunchao, Li Xueqin, Ma Xiaohui, Tian Yumin.High Precision North Seeking Scheme Based on Rotation Modulation [J] .Chinese Journal of Inertial Technology, 2010，18(4)：421-424.)

[2] 王立冬，刘 军，鲁 军.多位置寻北误差与陀螺数据采样时间的关系[J].中国惯性技术学报，2011, 19(3):286-289.(Wang Lidong, Liu Jun, Lu Jun. The Relationship between Multiposition North Seeking Error and Gyro Sampling Time [J] .Chinese Journal of Inertial Technology, 2011, 19(3):286-289.)

[3] 卜继军，魏贵玲,等. 陀螺寻北仪二位置寻北方案[J].中国惯性技术学报，2002, 10(3):46-49.(Bu Jijun, Wei Guiling, et al.Neither-north-seeking Scheme of Gyro North Finder [J] .Chinese Journal of Inertial Technology Chinese Inertial Technolog, 2002, 10(3): 46-49.)

[4] 陆元九.惯性器件[M]. 北京：国防工业出版社， 2002.(Lu Yuanjiu. Inertial Devices [M]. Beijing: National Defense Industry Press, 2002.)

[5] Titterton D H, Weston J L. Strapdown Inertial Navigation Technology[M]. Peter Peregrinus Ltd., on behalf of the Institution of Electrical Engineers, London, United Kindom, 1997: 268.

Research on Solver Algorithm for Flexible North Finder

Jia Zhixue,Zhang Xiaokai, Ren Jiajing

Ninth Academy of China Aerospace Science and Technology Company Institute 7107 Factory, Baoji 721006, China

Theflexiblenorthfindersolveralgorithmisstudiedinthispaper.Firstly,theprinciplesofcompositionandalgorithmofnorthfinderareintroduced,andonthebasisoftheestablishmentoftheerrormodelofgyroscopeandaccelerometer.Regardingthetwo-positionnorth-seekingmethod,thenorth-seekingalgorithmisderivedforthenorth-seekingsysteminthecaseofbaselevelandinclination,andtheexperimentresultsshowthatthealgorithmcanmeettherequirementsoflowprecisionlevel.

Flexiblegyroscope;Northfinder;Northfindertechnologysolutions;Errormodel;Experiment

2016-09-08

贾智学(1976-)，男，陕西宝鸡人，本科，高级工程师，主要研究惯性仪表；张小凯(1967-)，男，陕西户县人，硕士，研究员，主要研究惯性仪表；任佳婧(1989-)，女，黑龙江佳木斯人，硕士，助理工程师，主要从事导航、制导与控制研究。

TP23

A

1006-3242(2017)01-0082-04