基于超快精密星历的空间信号完好性监测算法*

李晓宇 董绪荣 帅玮祎 刘烜塨

1. 北京航天飞行控制中心, 北京 1000942. 装备学院，北京 101416



基于超快精密星历的空间信号完好性监测算法*

李晓宇1,2董绪荣2帅玮祎2刘烜塨1

1. 北京航天飞行控制中心, 北京 1000942. 装备学院，北京 101416

针对北斗卫星导航系统空间信号完好性监测问题，提出一种新的基于超快精密星历的空间信号完好性监测(UPSIM)算法。通过将超快精密星历与广播星历之差映射到用户方向求取空间信号监测阈值，建立了数学模型，并采用北斗卫星导航系统超快精密星历进行了算法验证。实验结果表明，采用UPSIM算法可以实现接收机端空间信号完好性的实时监测和预测，并有效识别卫星空间信号故障。

北斗卫星导航系统；完好性监测；空间信号；超快精密星历

随着全球卫星导航系统(Global Navigation Satellite System, GNSS)建设的全面开展以及新技术的出现，使得定位精度能够满足大部分用户需求。但由于GNSS系统故障、信号遮挡等问题，使得决定用户安全性能的导航系统完好性问题变得日益突出[1]。完好性(Integrity)是指导航系统发生任何故障或者误差超限，无法用于导航和定位时，系统向用户及时发出报警的能力[2]。

借鉴全球定位系统(Global Positioning System, GPS)标准性能规范的定义[3]，这里将北斗卫星导航系统空间信号完好性定义为：北斗卫星导航系统服务空间信号所提供信息正确性的信任程度，即当空间信号不能用于服务时，空间信号能向接收机提供实时告警能力。空间信号完好性是描述导航卫星提供导航服务的可靠性，是在伪距域的描述，是对空间信号误差(Signal in Space Error, SISE)的监测[4]。空间信号误差主要包括卫星轨道误差和钟差，在卫星覆盖范围内投影到视线方向，是时间与用户位置的函数。

目前空间信号完好性监测主要包括利用地面站对空间信号误差进行包络计算，以及在最差用户位置进行空间信号误差投影。相关的研究包括：GPS空间信号误差计算方法改进[5]；采用精密星历进行SISE的统计分析[6-8]；径向、切向和法向3个方向误差的相关性分析[9]；最差用户位置计算模型与算法的改进[10-11]，同时针对北斗区域星座以及单星故障率高的问题，部分学者开展了相关研究[12-14]。

可以看出，传统的方法需要计算最差用户位置和最差可视卫星，计算结果比较保守，一定程度上影响了系统的连续性。本文提出一种基于超快精密星历的空间信号完好性监测(UPSIM)算法。通过将超快精密星历与广播星历之差映射到用户方向，求取空间信号监测阈值，建立了数学模型和算法实施流程，该算法的优点是可以在用户位置实时地进行完好性性能预测。

1 iGMAS超快精密星历

精密星历是由若干地面跟踪站的观测数据,经事后处理算得的供卫星精密定位等使用的卫星轨道信息。GPS精密星历产品主要由国际GNSS服务(International GNSS Service, IGS)发布，IGS星历产品分为事后高精度精密星历、快速预报星历和超快精密星历。其中超快精密星历属于“实时+预报”产品，其预报部分轨道精度为5cm；实测部分精度可以达到3cm[15]。北斗卫星导航系统建设较晚，因此和GPS相比，在精密星历产品方面也相对滞后。国际全球卫星导航系统监测评估服务(international GNSS Monitoring Assessment Service，iGMAS)系统是我国提倡建立的全球四大卫星导航系统监测评估系统，旨在为全球用户提供精密星历钟差产品和系统服务性能监测。随着iGMAS系统的建设，北斗卫星导航系统的超快精密星历产品也逐步生成[16]。

武汉大学(WHU)是iGMAS系统数据中心之一，可以同时获得GPS和BDS多模观测数据，并利用自主研制的PANDA软件进行BDS精密定轨研究，解算获得BDS精密星历产品。目前WHU基于iGMAS观测站数据已经进行了超快精密星历的研究，生成了超快精密星历产品。通过系统内部测试，北斗倾斜轨道和中轨道卫星精密定轨精度小于0.1m，地球同步轨道精度小于0.2 m，可以作为本文完好性监测的基准超快精密星历使用[17]。下面对WHU生成的超快精密星历精度进行分析。

选取2015年6月1日的超快精密星历, 在IGS的ftp服务器下载事后精密星历产品com18472.sp3文件，选择C08号BDS卫星，分别对轨道和钟差误差进行评估，结果如图1～ 4所示。

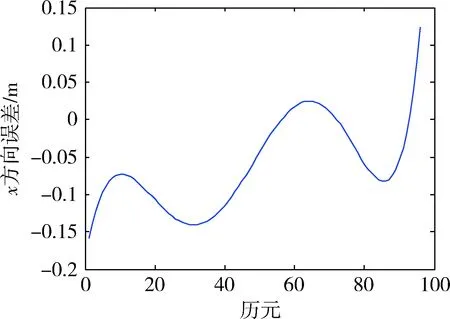
图1 卫星轨道x方向误差

图2 卫星轨道y方向误差

图3 卫星轨道z方向误差

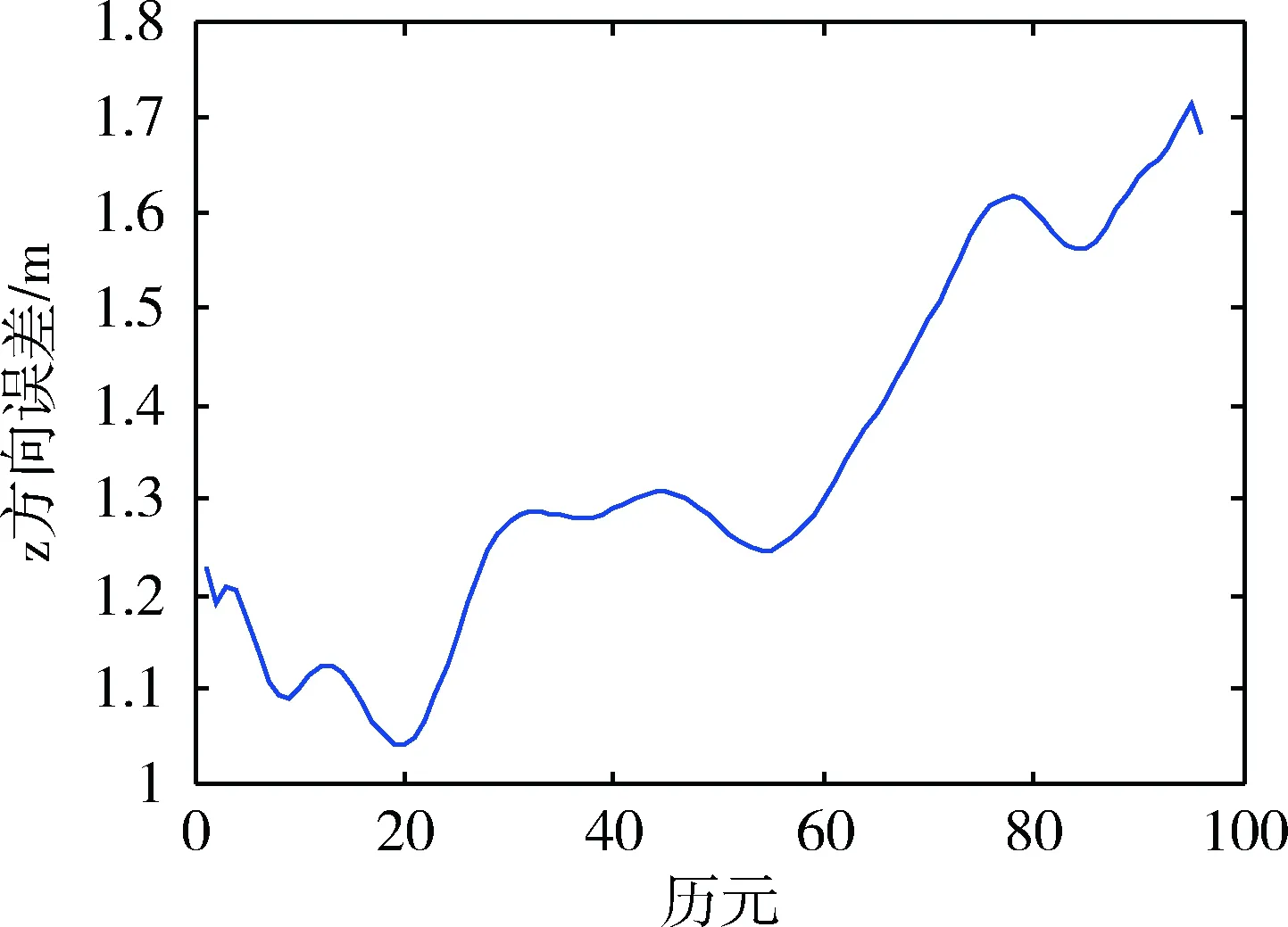
图4 卫星钟差误差

由图1～4可以看出，卫星轨道误差在0.02～0.15 m之间，三维误差为0.097 m；钟差误差在1.1～1.7 m之间，均值为1.34 m。超快精密星历精度远大于广播星历精度，可作为基准值对空间信号误差进行监测。

2 卫星空间信号完好性监测

2.1 空间信号误差阈值的确定

利用UPSIM算法监测空间信号(Signal in Space, SIS)完好性和识别卫星SIS故障，首先要计算卫星测距误差的阈值。如果卫星测距误差大于阈值，则相应的卫星被标记为“不可用”，这些卫星的观测值会从导航解方程中移去。

(1)

(2)

由式(1)和(2)可以看出，SIS误差可以转化为用户位置的卫星SIS测距误差，即SIS误差对卫星测距的影响可以确定。

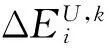
(3)

(4)

式中，Kpfa表示对应于故障告警率的系数，例如当故障告警率为10-7时，Kpfa=5.33；σε表示剩余误差，如电离层、对流层、多路径、干扰以及接收机误差。

2.2 计算保护限值

当地坐标系下的用户观测方程可以表达为

Y=GX0+ε

(5)

式中，X0表示待求解的用户坐标和钟差参数。采用最小二乘估计，方程的解可表示为

(6)

式中，

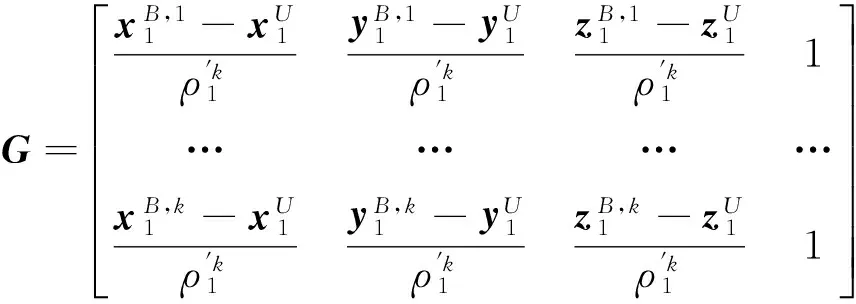
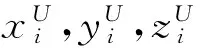
(7)

水平和垂直方向的保护限值可以表示为

(8)

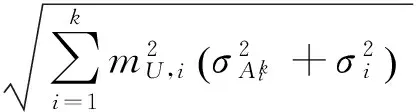
(9)

式中，

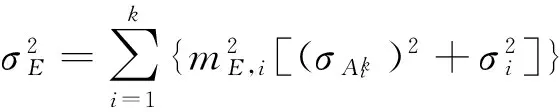
σi为除去卫星轨道和钟差外的剩余误差之和。

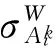
2.3 卫星故障诊断与监测

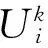
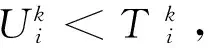
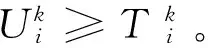
4)如果有多颗卫星被标记为“不可用”，在导航方程中取出最大测距误差对应的卫星观测值。然后重新计算导航解，求出新的卫星测距误差。

由上述算法可知，基于超快精密轨道和广播星历用户可以采用UPSIM可用性和保护限值的形式来预测完好性性能。当可见卫星的数目大于4，而且相应的精密预报轨道可用时，UPSIM能进行可用预测。基于超快精密预报轨道和广播星历可以计算SISRA，用户可进行完好性性能的预测。如果预测的用户完好性性能在特定的时间窗口没有满足特定用户需求，则会发生告警，用户可以及时的采取其他办法来避免完好性问题的发生。

3 实验分析

为验证本文所提算法的有效性，选取2015年1月7日(DOY007)IGS站点九峰站(JFNG，经纬度：30.51°N，114.49°E)的BDS观测数据(jfng0070.15o，brdm0070.15p)，以及武汉大学分析中心生成的超快精密星历(whu18263_00.sp3，whu18263_06.sp3，whu18263_12.sp3，whu18263_18.sp3)，采用C/A码测量值，采样间隔为 30 s。分别计算水平/垂直定位限值(Horizontal/Vertical Protection Limit, HPL/VPL)，基于传统接收机自主完好性监测(Receiver Autonomous Integrity Monitoring, RAIM)的HPL/VPL，以及基于UPSIM的HPL/VPL。选取C09号卫星，在1100历元处加入轨道故障误差60 m，持续时间为150历元。

图5～6为C09号卫星故障PVT的性能，图7为可见卫星数。采用UPSIM算法和传统RAIM来计算未移去C09号卫星观测值JFNG站的保护限值。

图5 故障排除前水平方向性能分析

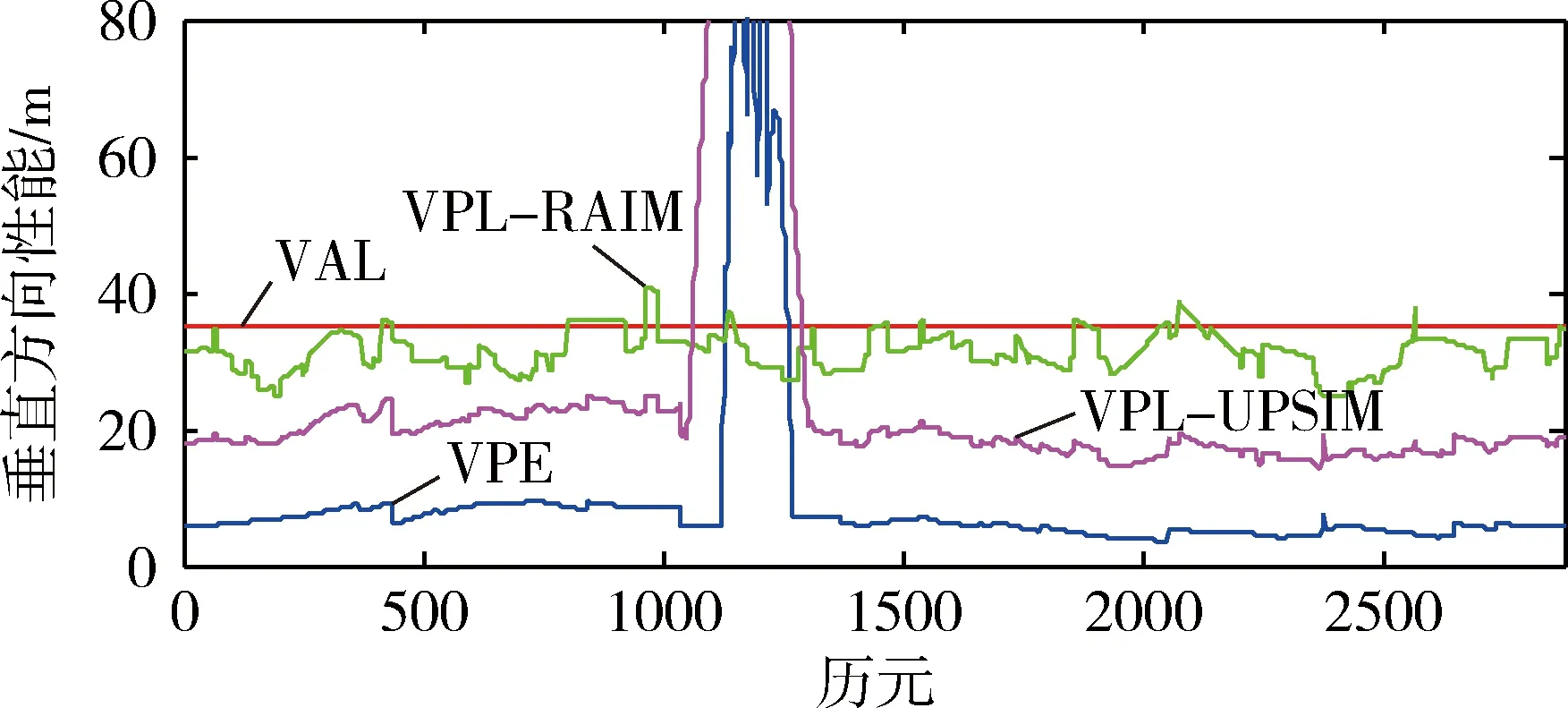
图6 故障排除前垂直方向性能分析

图7 可见卫星数

从图5～6可以看出，由于存在C09号故障卫星，HPL和VPL有一个大幅跳跃，定位误差也随之有很大的变化。但是正常情况下，当PL超过阈值时，接收机应该标记该卫星PVT为不可用。

图8～9显示了采用本文提出的UPSIM故障诊断与排除算法后JFNG站的PVT性能，C09号卫星的故障已被识别并排除。

图8 故障排除后水平方向性能分析

图9 故障排除后垂直方向性能分析

图8～9表明，采用新的算法移去C09号卫星观测值后，不存在完好性超限的问题，保护限值即使在危险时段也处于正常水平。采用C/A码观测值就可以成功识别出BDS C09号卫星的异常故障，并能从导航解中排除。

4 结论

提出的UPSIM算法可以基于C/A码对BDS卫星空间信号完好性实施监测，而不需要额外的地基或空基的完好性通道。采用UPSIM算法确定卫星SIS故障是基于广播星历与精密预报星历之差，将卫星空间信号误差转换到用户位置方向。由于该算法不需要考虑最差用户位置以及最差可视卫星，用户可以得到最优的完好性性能以及最佳的导航性能。为进一步优化UPSIM算法性能，下步可针对超快精密轨道精度优化及电离层、多径等误差模型修正开展相应的研究。

[1] 苏先礼. GNSS完好性监测体系及辅助性能增强技术研究[D].上海： 上海交通大学, 2013：12-14. (Su Xianli. The Research on GNSS Integrity Monitoring Theory and Assisted Performance Enhancement Technique[D].Shanghai:Shanghai Jiao Tong University, 2013: 12-14.)

[2] 秘金钟. GNSS完备性监测方法、技术与应用[D]. 武汉: 武汉大学, 2010: 5-11.(Bei Jinzhong. GNSS Integrity Monitoring Method，Technology and Application[D]. Wuhan: Wuhan University, 2010: 5-11.)

[3] William J. Global Positioning System (GPS) Standard Positioning Service (SPS) Performance Analysis Report[R]. Washington, D.C.:Federal Aviation Administration, 2007:410.

[4] 蒋春华,袁运斌,王海涛. GPS SIS完好性性能评估方法[J]. 导航定位学报, 2015, 3(3): 74-78.(Jiang Chunhua, Yuan Yunbin, Wang Haitao. Analysis and Assessment of GPS SIS Integrity Performance[J]. Journal of Navigation and Positioning, 2015, 3(3): 74-78.)

[5] 杨赛男,陈俊平,曹月玲. 空间信号精度的算法设计与实验分析[J]. 天文学进展, 2015, 33(2): 250-258.(Yang Sainan, Chen Junping, Cao Yueling. Calculation and Analysis of Signal- in-Space Accuracy[J].Progress in Astronomy, 2015, 33(2): 250-258.)

[6] Montenbruck, Oliver, Peter Steigenberger, and André Hauschild. Broadcast Versus Precise Ephemerides: A Multi-GNSS Perspective[C]. GPS Solutions 19.2 (2015): 321-333.

[7] Sun Si, Wang Zhipeng.Signal-in-Space Accuracy Research of GPS/BDS in China Region[C]. China Satellite Navigation Conference (CSNC) 2016 Proceedings: Volume II. Springer Singapore, 2016.

[8] Liu Shuai, Jia Xiaolin, Ma Zhuoxi. The Analysis of GNSS SIS Accuracy[C]. China Satellite Navigation Conference (CSNC) 2015 Proceedings: Volume I. Springer Berlin Heidelberg, 2015.

[9] 汪冬瑾,张英,刘建敬,李晓东. 一种改进的空间信号完好性监测算法[J]. 计算机测量与控制,2016,24(7):62-64，71.(Wang Dongjin，Zhang Ying，Liu Jianjing，Li Xiaodong. An Improved Signal-in-Space Integrity Monitoring Algorithm[J].Computer Measurement & Control， 2016,24(7):62-64，71.)

[10] 闫志跃, 喻国荣, 潘树国. Galileo完好性系统中WUL算法分析与改进[J]. 东南大学学报(自然科学版), 2013(增刊2): 414-417.(Yan Zhiyue, Yu Guorong, Pan Shuguo. Analysis and Modification of WUL Algorithm of Galileo Integrity System[J]. Journal of Southeast University(Natural Science Edition), 2013(Sup 2): 414-417.)

[11] 张雪辉,贝超,王芳. Galileo系统完好性参数SISMA的影响因素分析[J]. 航天控制, 2012, 30(6): 38-42.(Zhang Xuehui, Bei Chao, Wang Fang.Analysis of Factor of Integrity Parameter SISMA in Galileo System[J].Aerospace Control ，2012, 30(6): 38-42.)

[12] 杨晓义,李锐,黄智刚. BDS星座的完好性保护级改进算法[J]. 导航定位学报, 2016, 04(2): 67-70,80.(Yang Xiaoyi, Li Rui, Huang Zhigang. An Improved Algorithm of Integrity Protection Level for BDS Constellation[J].Journal of Navigation and Positioning, 2016, 04(2): 67-70, 80.)

[13] Liu Weiping, et al. A Method of Integrity Monitoring and Assessment for BeiDou Navigation Satellite System[C]. China Satellite Navigation Conference (CSNC) 2013 Proceedings. Springer Berlin Heidelberg, 2013.

[14] El-Mowafy, Ahmed. ARAIM for Vertical Guidance Using GPS and BeiDou[J]. J Glob Position Syst 12.1 (2013): 28-37.

[15] Ray J, Griffiths J. Status of IGS Ultra-Rapid Products for Real-Time Applications[EB/OL]. http://120.52.72.39/acc.igs.org/c3pr9ntcsf0/orbits/igu-products_aguf08.pdf.

[16] 苏行. iGMAS监测接收机数据质量分析方法及软件设计[D]. 西安: 中国科学院研究生院(国家授时中心), 2014: 75-77.(Su Hang. The Data Quality Check Methods of iGMAS Monitoring Receive and Software Implementation[D]. Xian: University of Chinese Academy of Sciences(National Time Service Center), 2014: 75-77.)

[17] Liu J, Ju B, Gu D, et al. BDS Precise Orbit Determination with iGMAS and MGEX Observations by Double-difference Method[J].Lecture Notes in Electrical Engineering,2014,305: 229-239.

[18] 孙晓剑. GNSS完备性监测RAIM算法研究[D]. 长沙: 中南大学, 2012: 23-24.(Sun Xiaojian. The Research on Receiver Autonomous Integrity Monitoring of GNSS[D]. Changsha: Central South University, 2012: 23-24.)

[19] Su H. Prediction of SBAS Integrity Performance Using PORIMA Algorithm[C]//Proceedings of the 23rd International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS 2010). Portland, OR: ION2010: 2056-2063.

Algorithm of Signal in Space Integrity Monitoring Based on Ultra Rapid Precise Ephemeris

Li Xiaoyu1,2，Dong Xurong2，Shuai Weiyi2， Liu Xuangong1

1. Beijing Aerospace Flight Control Center, Beijing 100094, China2. Equipment Academy, Beijing 101416,China

AccordingtothesignalinspaceofBeidounavigationsatellitesystem,theultrarapidpreciseephemerissignalinspaceintegritymonitoring(UPSIM)algorithmbasedonultrarapidpreciseephemerisisestablished;Bymappingthedifferencevaluebetweenpreciseephemerisandbroadcastephemeristouserdirection,thesignalinspacemonitoringthresholdcanbeobtained,andthemathmodelandalgorithmimplementationprocessareestablishedaswell,moreover,theverificationofalgorithmisfinishedbyadoptingBSDultrarapidpreciseephemeris.TheresultsshowtheemploymentofUPSIMalgorithmcanrealizethereal-timemonitoringofsignalinspaceintegrityatreceiverandeffectivelyidentifythesatellitesignalinspacefailures.

Beidounavigationsatellitesystem(BDS);Integritymonitoring;Signalinspace;Ultrarapidpreciseephemeris

*国家自然科学基金(41274043)

2016-08-12

李晓宇(1987-)，男，山东人，博士，工程师，主要研究方向为卫星导航定位、数据处理；董绪荣(1962-)，男，山东人，博士，教授，主要研究方向为卫星导航、精密定轨；帅玮祎(1991-)，女，河北人，博士研究生，主要研究方向为GNSS监测评估；刘烜塨(1984-)，男，河北人，硕士，工程师，主要研究方向为卫星测控与数据处理。

TN976.1

A

1006-3242(2017)01-0048-06