基于μ综合的高超声速飞行器控制律设计

王宇航 王晓东 张惠平 刘孟语

北京航天自动控制研究所，北京100854



基于μ综合的高超声速飞行器控制律设计

王宇航 王晓东 张惠平 刘孟语

北京航天自动控制研究所，北京100854

针对高超声速飞行器再入过程中飞行包线大，参数不确定性强等特点，设计一种利用不确定系统建模和μ综合控制的鲁棒姿态控制器。首先，考虑飞行器的参数不确定性，建立系统线性分式变换(LFT)模型。随后，考虑建模结构不确定性及测量噪声等的影响，建立用于μ综合控制的互联结构。最后，分别设计H∞控制器和μ综合控制器，结合频域μ分析方法对系统鲁棒性和动态性能作了对比分析，结果表明该方法可以很好地跟踪指令，具有较强的鲁棒稳定性。

高超声速飞行器；μ综合控制；结构不确定性；线性分式变换

RLV高超声速飞行器再入过程中，飞行高度和马赫数跨度范围大，气动参数变化剧烈，由此带来较大的不确定性。传统控制系统设计通常基于物理模型，未能充分将参数的不确定性考虑到控制建模过程中，系统的鲁棒性难以保证。

鲁棒控制方法充分考虑系统在受扰情况下的鲁棒性能，在处理解决模型不确定问题和鲁棒控制问题中获得了成功的应用。常用的鲁棒控制方法包括H∞方法和μ综合方法[1-2]。其中，H∞控制可有效处理非结构不确定性问题，对于结构不确定性问题，则可能带来较大的保守性。μ综合控制方法可较好地解决H∞方法存在的保守性，并在干扰情况下保持较好的控制性能。

本文研究了μ综合的系统不确定建模，以克服传统H∞方法存在的保守性问题，并建立互联结构，采用D-K迭代方法，完成了高超声速再入飞行器的纵向鲁棒控制系统设计。

1RLV飞行器LFT建模

1.1 线性分式变换(LFT)

RLV飞行器模型中包含大量不确定性参数，不确定系统的建模需要将系统的不确定性从系统中剥离出来，在控制系统设计中予以考虑。采用LFT方法，将非线性的飞行器模型表达成合适的LFT反馈互联结构形式，从而实现这个过程[3]。

令M为复矩阵，可分块为：

(1)

定义复矩阵块结构Δl∈Cq1×p1，若逆(I-M22Δl)-1存在，则

Fl(M,Δl):=M11+M12Δl(I-M22Δl)-1M21

(2)

式(2)即为矩阵M关于Δl的上LFT形式，其含义为：Fl(M,Δl)有标称映射M11，并且被Δl所摄动，M11，M12和M21反映了摄动如何影响标称映射。

上LFT形式的结构如图1所示。

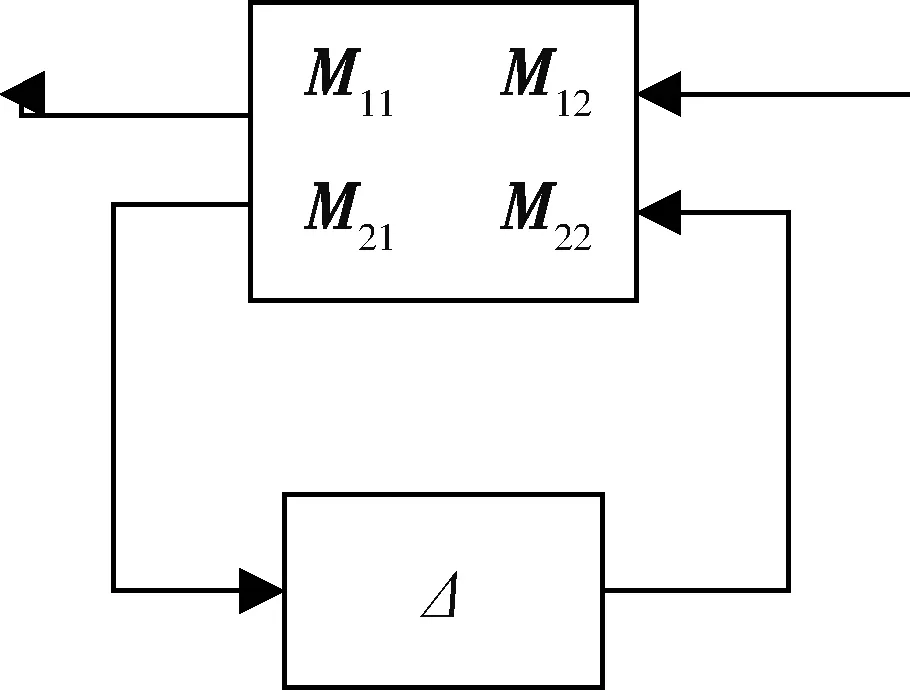
图1 上LFT结构图

1.2RLV飞行器参数不确定建模

基于LFT方法的不确定建模，不需要建立系统关于不确定参数摄动的解析表达式，是一种“黑箱建模”的方法，只需要系统的非线性模型能在不确定参数取不同值时进行有效的配平和线性化，得到线性化的系统矩阵，这种方法简单方便，其代价就是最终所建立的模型具有一定的保守性。采用μ综合方法进行鲁棒控制器设计前，首先需要建立飞行器状态矩阵的参数不确定模型[4-6]。

飞行器的一般线性化模型为：

(3)

其中，A0∈Rn×n，B0∈Rn×nu，C0∈Rny×n，D0∈Rny×nu为飞行器配平下的标称状态矩阵。考虑A0，B0，C0，D0中包含的参数不确定性，建立飞行器不确定模型为：

(4)

式中，参数不确定性反映在m个不确定参数δ1,…,δm中。δi需归一化处理，使δi∈[-1,1]。

则每个矩阵可分解为：

(5)

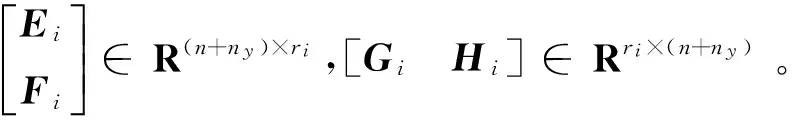
假设系统为M，则可将S(Δ)表示成Fl(M,Δ)的形式，

(6)

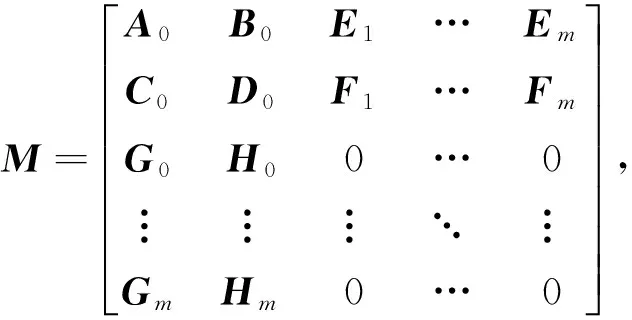
Δ=diag{δiIi}。

将系统表示为M，则状态方程表示的输入输出连接关系可表示为图2。

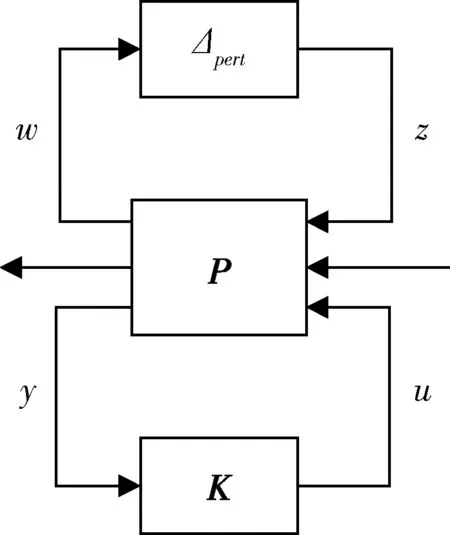
图2 控制系统LFT表示

RLV飞行器再入过程中，俯仰通道相对独立，一般单独进行设计。主要受气动力、力矩系数、质量、惯性力矩等不确定性的影响，可将飞行器模型描述成如式(7)的关于不确定参数的状态方程矩阵：

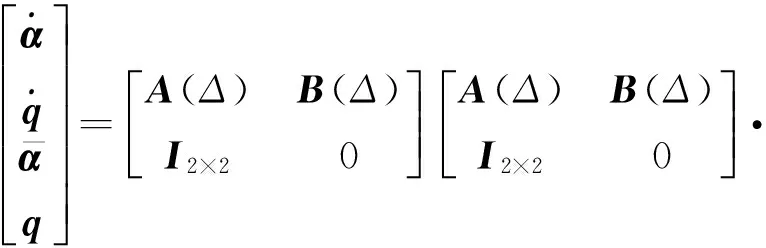
(7)

2 基于μ综合方法的鲁棒控制系统

2.1 结构奇异值与μ综合

对图3所示系统，若Δ不是块对角结构，根据小增益定理，系统稳定的条件为M∞≤1。本文中，实际考虑Δ是一种对角结构的结构不确定性，因此H∞理论中的奇异值(或H∞范数)条件具有保守性。为此，将奇异值的概念推广，定义1个新的量μΔ(M)，称为结构奇异值。与常规的H∞设计中要求系统的最大奇异值的最小值小于1类似，图3系统稳定的充要条件为

supμΔ[M(jω)]<1

(8)

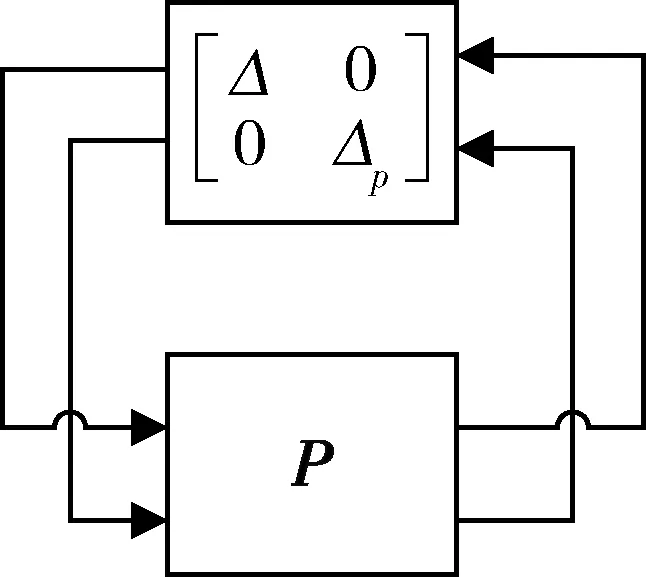
图3 结构不确定性问题

根据式(8)的要求来设计控制器K的方法称为μ综合。

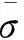
(9)

通常，μ值由上界来求取，μ综合方法即为求解式(10)的优化问题：

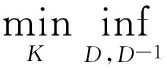
(10)

2.2μ综合控制系统设计

考虑RLV飞行器再入过程中俯仰通道的控制，μ综合控制系统设计即转化为在具有模型输入端乘性不确定性和输出权函数最低性能标准下的鲁棒性能约束和模型匹配问题。包括模型和控制器的RLV飞行器纵向姿态控制系统的闭环反馈结构图如图4所示。

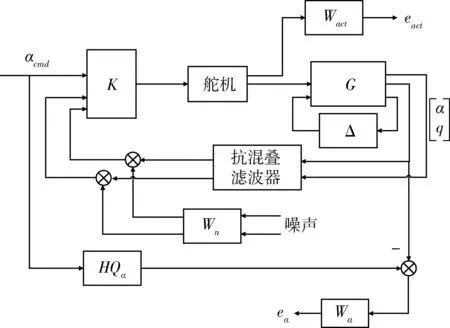
图4 飞行器纵向控制结构图

图中，(G,Δ)为考虑参数不确定性的飞行器LFT模型，HQα为理想跟踪模型，Wact为舵机权函数，Wα为性能权函数，Wn为噪声权函数，αcmd为输入指令。在图4的μ结构框架中，性能目标函数通过求解权函数的范数来获得。权函数有2个作用：范数相同下，直接比较性能目标函数；在性能分析中加入了频率信息。权函数的选取如下：

1) 理想跟踪模型：攻角对指令的响应，通常表示为一阶或二阶系统的形式。根据飞行器的控制性能要求，本文选取

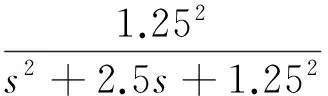
(11)

2) 抗混叠滤波器：加入抗混叠滤波器，可在采样频率f一定的前提下，通过低通滤波器滤掉高于f/2 的频率成分，避免出现频率混叠。结合系统俯仰通道的截止频率，取

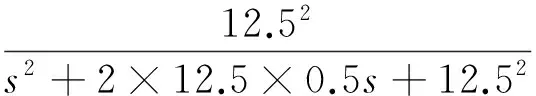
(12)

3) 舵机权函数：对升降舵的舵偏角和舵偏角速率进行限制，为2×2的对角常数矩阵。取

(13)

4) 噪声权函数：反映传感器量测噪声的影响。为反映噪声值随着频率增加而增大，选取噪声权函数

(14)

5) 输出端跟踪性能权函数：在μ结构中，期望的δele-to-q和δele-to-α响应与实际响应构成模型匹配问题，需要使期望响应输出和飞行器实际响应输出的偏差最小。为使系统具有良好的指令跟踪能力和抗干扰能力，应使低频段的幅值较大，高频段幅值较小。对俯仰角速率偏差加权处理

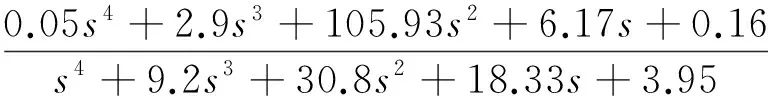
(15)

式中，Wα在0.06～30rad/s频率范围内幅值较大，期望的攻角跟踪误差在5%以内。

确立了飞行器LFT参数不确定模型和不确定权矩阵后，在Matlab中通过sysic语句构建图4所示内联结构[4]。随后应用D-K迭代方法，进行μ综合控制器的设计。闭环系统的性能通过计算扰动和指令输入与误差输出间的加权函数的最大结构奇异值得到。μ综合方法设计的目标，即令所有的性能权函数H∞范数不超过1。

3 仿真分析

为了检验μ综合控制器的性能，本文以某型航天飞机六自由度仿真模型为研究对象，分别采用H∞方法和μ综合方法设计控制器，并进行对比分析。

选取飞行器再入过程中某一飞行状态点H=42000,Ma=5,α=35°，最终控制目标在参数偏差和系统结构不确定性下精确跟踪攻角指令，保证飞行控制系统稳定，并具有较好的鲁棒性。仿真中取参数具有最大不确定性，如表1所示。

表1 不确定项

3.1 频域鲁棒性分析

采用μ分析方法做出闭环系统鲁棒稳定性曲线[4,7]。由于结构奇异值的计算比较困难，因此常采用计算其上下界的方式来逼近真实值。分别考虑摄动不确定矩阵为复数和实数块时，得到闭环系统的μ值曲线，如图5和6。从图5可以看出，复数摄动时，H∞控制器在低频处有较大的峰值，且超过1，但在高频处μ值较小，表明它能较好地抑制系统的高频噪声。μ综合控制器是以μ值作为优化指标进行设计，从图6中也可以看出，相对于H∞方法，μ综合控制具有更好的鲁棒稳定性。

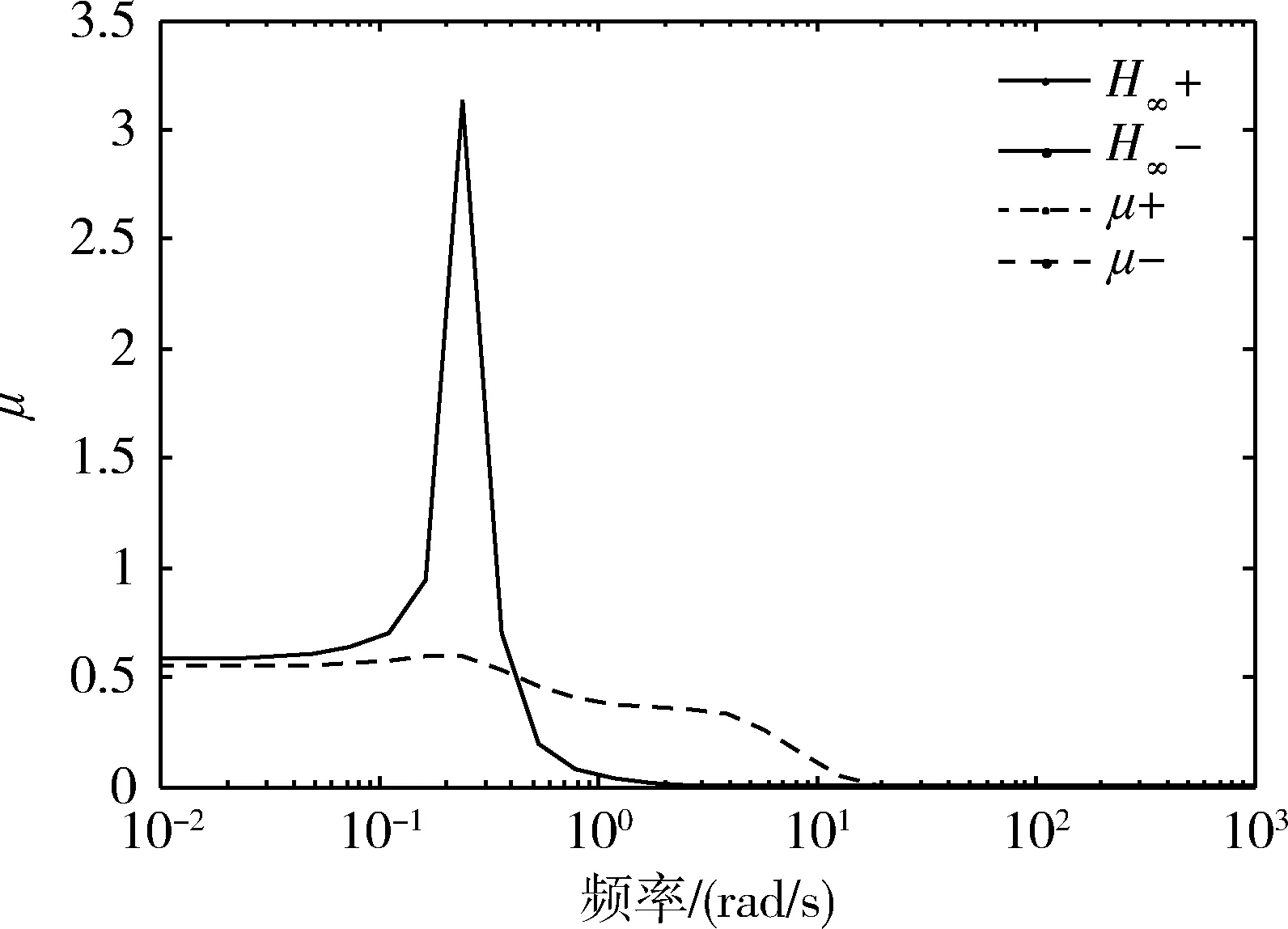
图5 复数摄动下，闭环系统μ值曲线

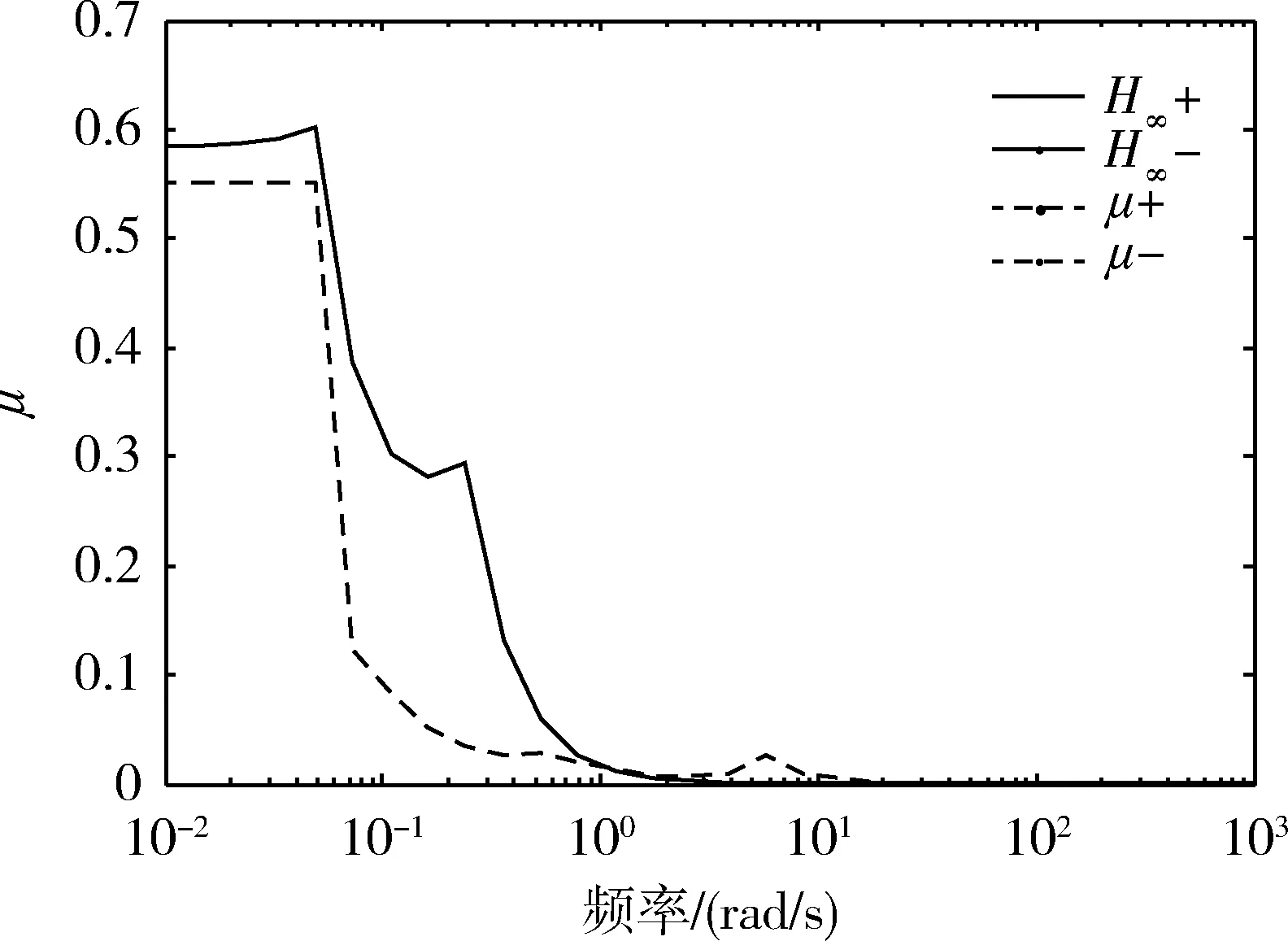
图6 实数摄动下，闭环系统μ值曲线

3.2 时域性能分析

针对俯仰通道非线性不确定模型，输入攻角指令信号，得到系统在标称状态和最差扰动下的响应曲线，如图7所示。其中，最差扰动为在所有不确定性和扰动的组合中，使得系统H∞范数最大时的响应。

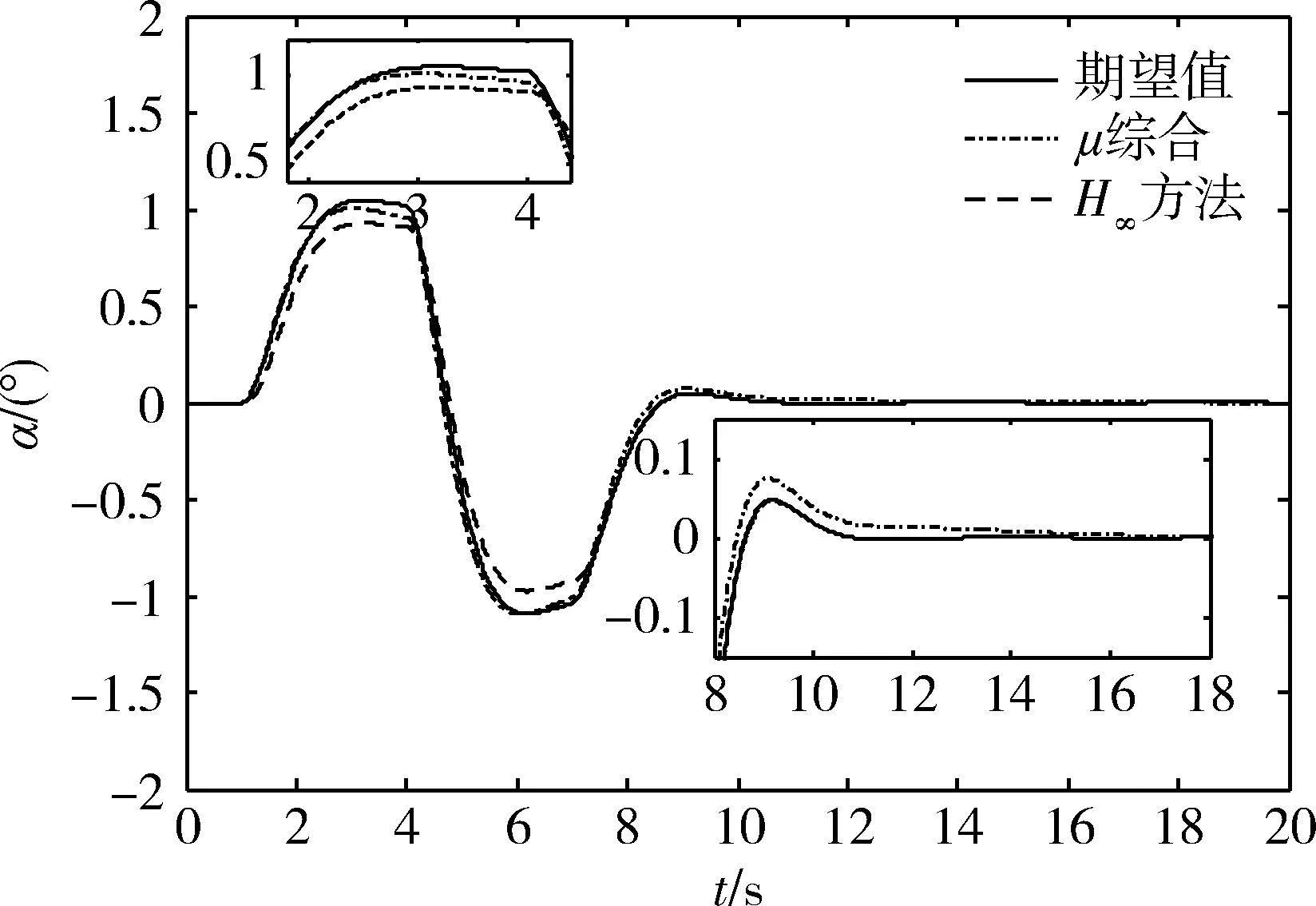
图7 标称状态下控制效果对比

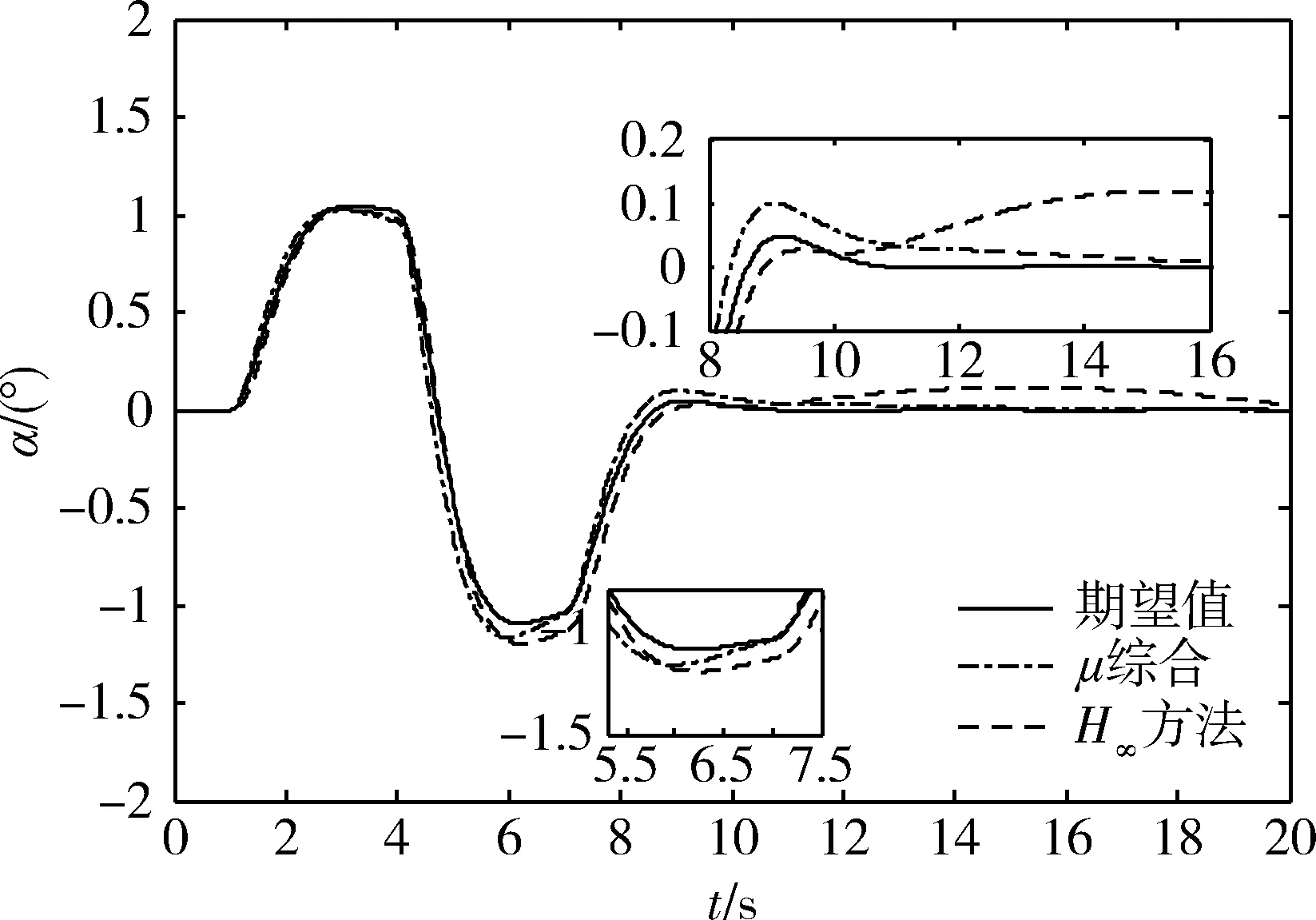
图8 扰动状态下控制效果对比

图7和8中，实线为理想输出曲线，点划线为标称状态输出，虚线为最差扰动输出。从图中可以看到，标称和扰动情况下，攻角响应均满足理想跟踪模型的时域设计指标，且最差扰动响应与标称响应的差别较小，显示了较好的抗不确定性。同时，飞行器攻角跟踪偏差始终保持在0.2°以内，且收敛速度很快，满足高超声速飞行器的俯仰通道控制精度要求。

4 总结

针对高超声速飞行器再入过程的较大不确定性，建立了飞行器LFT模型，并加入性能权函数构建系统设计框架，完成了鲁棒μ综合控制律的设计。通过与H∞控制器在时域和频域的仿真比较，说明了μ综合控制能很好地解决系统的鲁棒稳定性问题，且具有良好的动态性能，表明该设计方法具有一定的应用价值。

[1]TengYing,ChenHsin-Piao.Mu-SynthesisforAnActiveAeroelasticWingwithLeadingandTrailingEdgeControlSurfaces[C]. 44thAIAAAerospaceSciencesMeetingandExhibit9-12January2006,Reno,Nevada. 2006.

[2]FrancescoAmato,RaffaeleIervolino.μSynthesis for a Small Commercial Aircraft: Design and Simulator Validation[J]. Journal of Guidance Control and Dynamics, 2004, 27(3):479-490.

[3] 周克敏, J. C. Doyle, K. G. Glover. 鲁棒与最优控制[M]. 北京: 国防工业出版社, 2006.(Zhou Kemin, J. C. Doyle, K. G. Glover. Robust and Optimal Control [M]. Beijing: National Defense Industry Press, 2006.)

[4] Gary J. Balas, John C. Doyle, Keith Glover, et al.μ-AnalysisandSynthesisToolbox[M].Minneapolis,MN:TheMUSYNIncandtheMathWorksInc, 2001.

[5] 王章磊, 罗建军, 苏二龙. 高超声速再入飞行器不确定性分析与μ综合控制[J]. 西北工业大学学报, 2013, 31(4): 571-576.(WangZhanglei,LuoJianjun,SuErlong.UncertaintyAnalysisandμSynthesisRobustControllerDesignforHypersonicRe-EntryFlightVehicle[J].JournalofNorthwesternPolytechnicalUniversity, 2013, 31(4): 571-576.)

[6] 张永康, 李中健. 基于LFT的鲁棒飞行控制系统设计与仿真研究[J]. 计算机仿真, 2008, 25(10): 31-34,45. (ZhangYongkang,LiZhongjian.DesignandSimulationofRobustFlightControlBasedonLFT[J].ComputerSimulation, 2008, 25(10): 31-34,45.)

[7] 史丽楠, 张冉, 李惠峰. 再入滑翔飞行器控制系统鲁棒性能评估方法研究[J]. 航天控制, 2015, 33(2): 44-49,55.(ShiLinan,ZhangRan,LiHuifeng.ResearchontheAssessmentMethodofRobustPerformanceofGlidingReentryAircraftControlSystem[J].AerospaceControl, 2015, 33(2): 44-49,55.)

RobustμSynthesisControllerDesignforHypersonicFlightVehicle

WangYuhang，WangXiaodong，ZhangHuiping，LiuMengyu

BeijingAerospaceAutomaticControlInstitute,Beijing100854,China

Aimingatthelargeflightenvelopeandstronguncertaintiesofaerodynamicparametersandatmosphericenvironmentduringthehypersonicflightvehiclereentryprocess,arobustcontrollerwhichcombineslinearfractionaltransformation(LFT)withμsynthesisisintorduced.Firstly,parameteruncertaintiesoftheflightvehicleareconsideredtoformaLFTmodel.Then,bytakingstructureuncertaintiesandsensornoiseintoaccount,thecontrolblockdiagramforμsynthesiscontrolisformed.Finally,H∞controllerandμsynthesiscontrolleraredesignedseparatelytobecomparedandanalyzedbytherobustperformanceanddynamiccapabilityoftheclosed-loopsystemusingμanalysismethods.Thesimulationresultsshowthatthiscontrolsysteminstructionscanbetrackedwellandthismethodhasstrongrobustness.

Hypersonicvehicle;μsynthesiscontrol;Structureuncertainties;Linearfractionaltransformation

2016-08-26

王宇航(1991-)，男，河北人，硕士研究生，主要研究方向为飞行器姿态控制、系统辨识；王晓东(1969-) ，男，西安人，研究员，主要研究方向为飞行器控制、制导与仿真；张惠平(1979-)，男，宁夏人，硕士，高级工程师，主要研究方向为飞行器姿态控制与仿真；刘孟语(1991-)，女，安徽人，硕士研究生，主要研究方向为自主可控控制系统。

TP

A

1006-3242(2017)01-0020-05