近圆参考轨道脉冲悬停及其轨迹安全分析方法

程 博 袁建平 钱霙婧 马卫华

1.西北工业大学，西安 7100722.北京宇航系统工程研究所, 北京 1000763.航天飞行动力学技术重点实验室, 西安 7100724.北京工业大学，北京100124



近圆参考轨道脉冲悬停及其轨迹安全分析方法

程 博1,2,3袁建平1,3钱霙婧4马卫华1,3

1.西北工业大学，西安 7100722.北京宇航系统工程研究所, 北京 1000763.航天飞行动力学技术重点实验室, 西安 7100724.北京工业大学，北京100124

基于航天器相对运动的C-W方程及其解析解，研究了空间相对悬停的脉冲控制方法，给出了相对悬停脉冲控制量的计算方法，降低了对空间悬停任务航天器控制推进系统的要求，有利于工程实现。以两航天器相对轨道机动过程中的碰撞概率计算方法为基础，对相对悬停的轨迹安全风险进行了量化分析。数值仿真算例显示，本文方法可实现圆或近圆参考轨道上的空间相对悬停，且缩短悬停轨道机动周期，有利于悬停效果的提升。悬停相对运动过程中，悬停碰撞概率的极值点与两航天器相对距离的最小值几乎同时出现。

近圆轨道；相对悬停；脉冲；碰撞概率；轨迹安全

随着人类对空间研究、开发与应用能力的不断提升，各国开展的及计划开展的航天任务的复杂程度不断提高，研制的航天器在结构、组成和性能等方面的技术水平不断进步。因此，对于以在轨燃料加注、维护修复、功能更换和升级以及在轨组装等为内容的在轨服务技术的需求越来越迫切[1]。

作为在轨服务技术重要支撑的航天器相对悬停技术逐渐成为航天工程领域的研究热点。航天器相对悬停是指通过力和力矩控制，保持主动航天器相对目标航天器的位置始终保持不变，仿佛是静止悬停于某个固定点上[2]。

目前，针对航天器悬停技术的研究主要基于连续推力条件，要求主动航天器的推进系统能够提供大小和方向均连续可变的控制加速度。在实际工程应用中，以现有的航天器控制推进技术，实现对轨道控制推力的连续精确调节仍非常困难。因此近年来有学者基于线性相对运动模型，开展了航天器悬停的脉冲推力控制方法研究[3-4]。

在对航天器相对悬停的控制方法进行研究的同时，其轨迹安全也是需要重点关注的方面。尤其是近距离相对悬停的航天任务，相对标称悬停点的偏离以及相对悬停的轨道机动过程都极有可能导致两航天器发生碰撞，产生灾难性后果。基于碰撞概率的思想，多位学者研究了空间目标相对运动的安全问题，给出了空间相对运动安全性的量化方法[5-7]。

本文基于航天器相对运动C-W方程的解析解，给出了航天器相对悬停的脉冲方法，实现了脉冲推力作用下的圆或近圆参考轨道的空间相对悬停控制。首先介绍了航天器空间相对运动的C-W方程及其解析解，建立了相对运动的状态转移矩阵描述形式，在此基础上推导了基于相对运动状态转移矩阵的悬停脉冲控制量线性计算方法，用以确定脉冲悬停的轨道转移速度脉冲增量。其次，基于量化的碰撞概率模型给出了空间相对悬停运动的轨迹安全分析方法，建立了碰撞概率密度模型，并在航天器结构球形包络及总包络球内的概率密度均匀的条件下给出了相对悬停运动的碰撞概率计算方法，用于相对悬停的轨迹安全分析。

本文提出的方法可采用具备多次启停功能的大推力轨控发动机实现轨道机动的冲量控制，有利于工程实现。基于碰撞概率的相对悬停轨迹安全分析方法能够对风险进行量化，分析结果相对可靠。数值仿真算例显示，该方法可满足圆或近圆参考轨道下一定精度的空间相对悬停任务的控制需求，碰撞概率与悬停运动的相对位置相关，对轨迹安全的分析相对更加客观和可信。

1 相对悬停动力学

为了对航天器悬停的相对运动过程进行描述，引入J2000地心赤道惯性坐标系O-XYZ(简称“惯性坐标系”)和目标航天器质心轨道坐标系o-xyz(简称“轨道坐标系”)。如图1所示，惯性坐标系的原点在地心O上，X轴在赤道面内指向春分点，Y轴在赤道面内与X轴垂直指向东，Z轴与X轴、Y轴构成右手正交坐标系。轨道坐标系的原点在目标航天器质心o上，x轴沿地心指向目标航天器方向，y轴在轨道平面上与x轴垂直，指向航天器的速度方向，z轴和x轴、y轴构成右手正交坐标系。

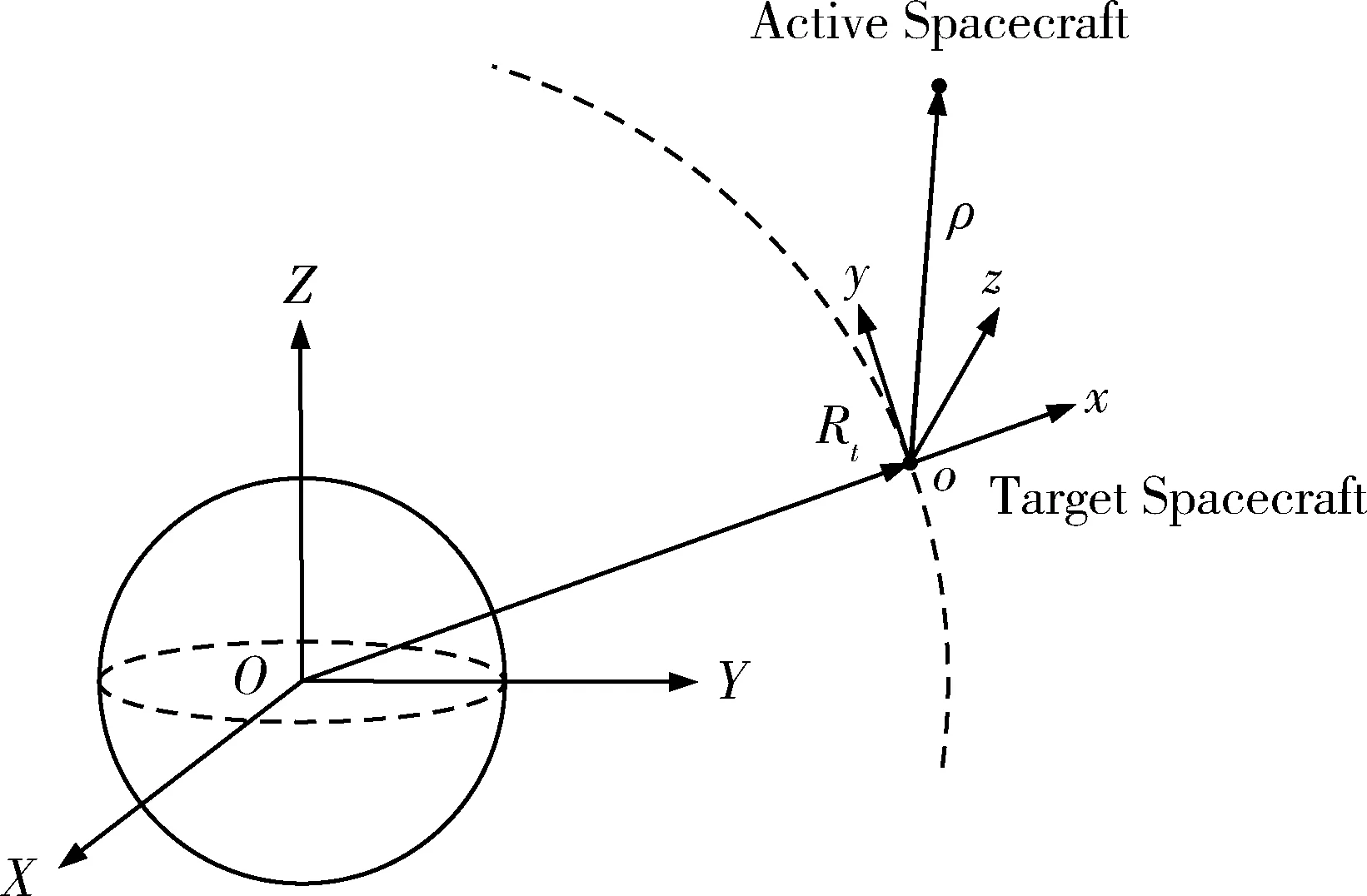
图1 航天器悬停坐标系(交换了y轴和z轴)

如图1所示，在目标航天器轨道坐标系下，主动航天器相对目标航天器运动的动力学方程如下[8]：

(1)

对于一般的空间相对悬停任务，两航天器的相对悬停距离ρ及其分量与参考轨道半径相比为小量，故他们的模之比的二阶及二阶以上项为高阶小量，简化计算时可以略去，则式(1)可简化成：

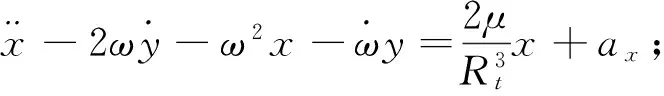
(2)

若参考轨道为圆或近圆轨道，则其轨道角速度为常值。

假设主动航天器不受外力作用，以自由飞行状态与目标航天器相对运动。对式(2)进一步简化得：

(3)

式(3)即为描述航天器相对运动的C-W方程，也称希尔方程(Hill’sequations)[9-10]。对式(3)的微分方程组进行求解，并将解析解写成状态转移矩阵的形式。

(4)

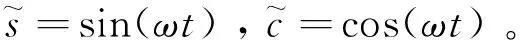
在相对运动初始时刻状态已知的情况下，应用式(4)可对任意时刻的相对运动状态进行求解。

2 脉冲悬停方法

航天器相对悬停的本质也是一种相对运动，只是悬停运动的相对位置始终保持不变。脉冲悬停是以航天器脉冲变轨的轨道机动形式进行相对位置控制的一种悬停方式。主动航天器在实施悬停控制时，在悬停点施加速度冲量进行脉冲变轨，其轨道转移的目标点仍设置为初始的悬停位置，当脉冲变轨的周期足够短或满足工程任务需求，则可近似认为2个航天器实现了“持续”的相对悬停。

将式(4)的相对运动状态转移矩阵写成矩阵组合的形式：

(5)

式中,4个子阵均为三维方阵，则式(4)可写成：

(6)

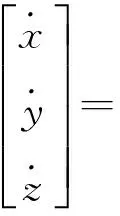
(7)

应用本节给出的脉冲相对悬停的概念，使主动航天器相对目标航天器轨道机动终止时刻的相对位置与初始时刻相同。则由式(6)可得：

(8)

式中，v0+为主动航天器进行悬停轨道机动时的初始速度，将其代入式(7)可得：

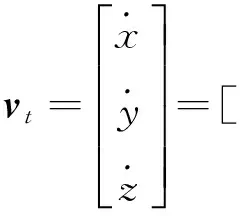
(9)

vt为相对悬停轨道机动终止时刻主动航天器相对目标航天器的速度。

对于相对悬停的2个航天器，主动航天器在施加速度脉冲实施悬停轨道机动前应相对目标航天器静止。主动航天器经过1个脉冲轨道机动再次到达目标悬停点后，仍要求相对目标航天器静止，则可得脉冲悬停的初始速度冲量Δv0和终止速度冲量Δvt分别为：

(10)

适当选择脉冲相对悬停的周期，持续循环实施相对悬停的轨道机动脉冲可以实现速度冲量控制下的近似相对悬停。

在求解脉冲悬停速度冲量的大小时，三维方阵φ12的可逆性是需要关注的问题。求解φ12的行列式，可得：

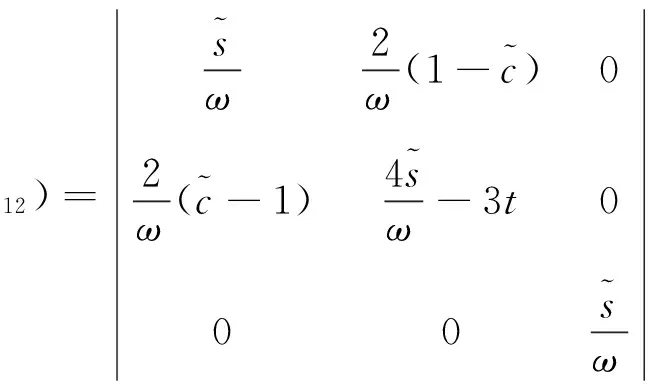
(11)

根据矩阵可逆的充要条件，当φ12的行列式det(φ12)≠0时，三维方阵φ12可逆。故式(12)中的条件应同时满足[11]，

(12)

为了得到近似持续的相对悬停，主动航天器轨道机动的周期应小于参考轨道周期，因此仅考虑相对运动时间t∈[0,2π/ω)的情况。由式(12)第1式可得相对运动的时间t≠0，则可将相对运动时间的讨论范围进一步缩小为一个开区间t∈(0,2π/ω)。下面对式(12)的第2式的不等式条件进行分析。

设θ=ωt，θ∈(0,2π)。对式(12)的第2式进行变量代换，并构造如下函数：

f(θ)=8-8cos(θ)-3θsin(θ)

(13)

对式(13)求一阶导，f′(θ)=0的点即为函数f(θ)的极值点。可得极值点对应的变量θm满足如下条件：

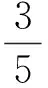
(14)

由式(14)可得，θm应为函数g(θ)=tan(θ)和直线h(θ)=3θ/5交点的横坐标，且在函数定义域θ∈(0,2π)内仅有1个交点，故函数f(θ)在其定义域内仅有1个极值点。

显然式(13)的函数f(θ)在θ∈(0,2π)连续，又f(0)=f(2π)=0，故函数f(θ)在其定义域内无零点，即式(12)的第2式在t∈(0,2π/ω)内成立。主动航天器相对目标航天器脉冲悬停时，轨道机动的周期t∈(0,2π/ω)时，φ12可逆。

3 基于碰撞概率的悬停轨迹安全分析

基于本文第2节的方法可以有效建立以脉冲推力为控制手段的航天器相对悬停系统。但该方法在理论推导时进行了简化，舍去了动力学模型中的高阶小量，会对悬停精度和稳定性产生影响。同时在实际的空间悬停任务中，因地球非球形引力摄动等各类空间摄动力对航天器轨道的影响，使得主动航天器相对目标航天器的悬停点会发生缓慢的“漂移”，给长期悬停任务，特别是近距离长期悬停任务的系统安全性带来无法忽视的影响。本节基于碰撞概率的思想，对相对悬停的轨迹安全进行分析。

设初始时刻主动航天器和目标航天器相对状态分布的协方差矩阵为CX0，轨道机动t时刻的相对状态分布的协方差矩阵为CXt。由式(4)可得2个协方差矩阵的传递关系:

(15)

相应的，相对位置随机向量的协方差矩阵CR为相对状态随机向量协方差矩阵CX的左上角3×3子阵。

(16)

为了计算相对悬停的2个航天器的碰撞概率，将航天器的外形简化成一个包络球，其球心为航天器质心。将目标航天器和主动航天器的包络球结合成一个总包络球V，其半径为2个航天器包络球半径之和。如果让目标航天器的质心与总包络球球心重合，则主动航天器相对目标航天器的相对位置落在总包络球内的部分表示2个航天器发射了碰撞。于是，相对悬停飞行器的瞬时碰撞概率可以通过在总包络球内对相对位置的概率密度函数式(16)进行积分获得。

(17)

如果总包络球内的相对位置概率密度较均匀，为简化计算，可以用总包络球球心处的概率密度近似代替整个总包络球的概率密度，则碰撞概率可用下式简化计算

(18)

在进行航天器悬停的轨迹安全分析时，预先设定碰撞概率的预警值Palarm，当2个航天器相对悬停运动的悬停点发生“漂移”，使得某时刻其瞬时碰撞概率大于预设的预警值，则实施轨道机动，修正悬停运动的悬停点，确保2个航天器相对悬停的安全性。

4 建模仿真

对文中给出的航天器相对悬停方法及相对悬停轨迹安全分析方法进行仿真。仿真算例中，目标航天器运行在圆轨道上，其轨道参数如表1所示。

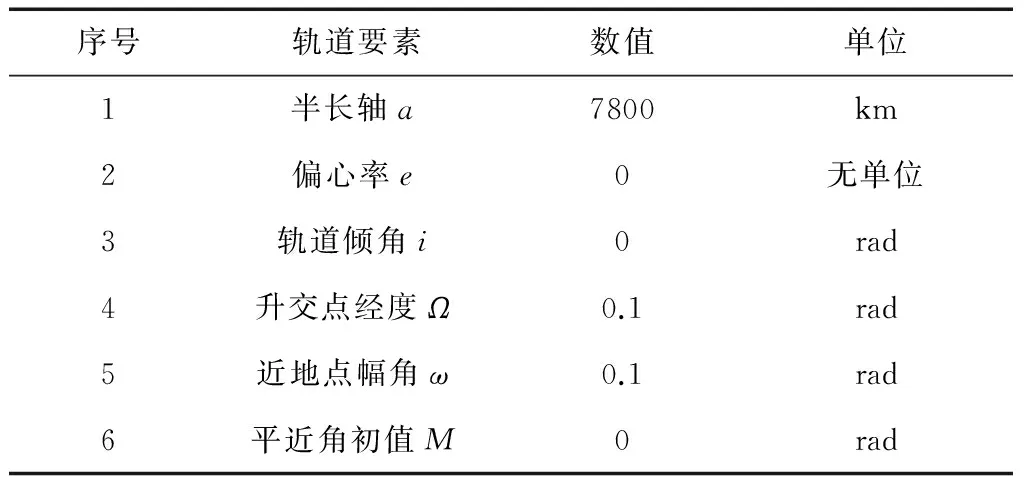
表1 目标航天器初始条件

4.1 航天器脉冲悬停

设初始时刻主动航天器相对目标航天器的位置ρ0(单位：km)和速度v0(单位：km/s)在目标航天器轨道坐标系下的分量分别为：

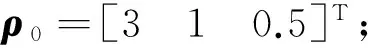
理论悬停点d与2个航天器初始时刻的相对位置ρ0相同。分别选择在1个轨道周期内进行5次、10次和20次脉冲悬停，且每次脉冲变轨时间相同。图2给出了主动航天器相对目标航天器脉冲悬停的相对运动轨迹的仿真结果。

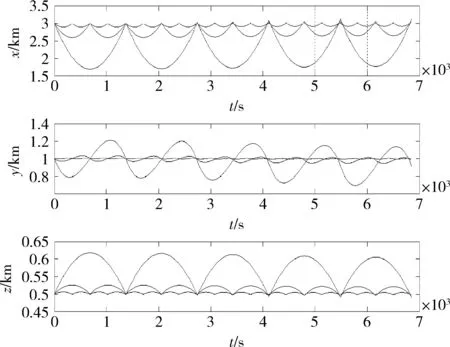
图2 脉冲悬停相对运动轨迹

由图2可知，主动航天器相对目标航天器的每一次相对运动，其起点和终点都在预先设定的悬停点附近，且悬停脉冲数越多，相对运动轨迹越平滑，即主动航天器在悬停点附近的相对运动越稳定。本文给出的航天器悬停方法可有效实现圆或近圆参考轨道上的脉冲相对悬停。

4.2 相对悬停轨迹安全分析

设相对悬停的初始相对位置和速度与上例相同。总包络球半径为100m，初始时刻的相对状态中相对位置测量量的标准差为150m，相对速度测量量的标准差为0.25m/s，则初始时刻相对状态协方差矩阵的对角线元素为其对应相对状态标准差的平方，非对角线元素均为0。

选择在1个轨道周期内进行4次脉冲悬停，连续进行8次脉冲悬停轨道机动。图3给出了这8次脉冲悬停轨道机动过程中主动航天器相对目标航天器相对距离的大小，图4给出了轨道机动过程中碰撞概率的变化情况。

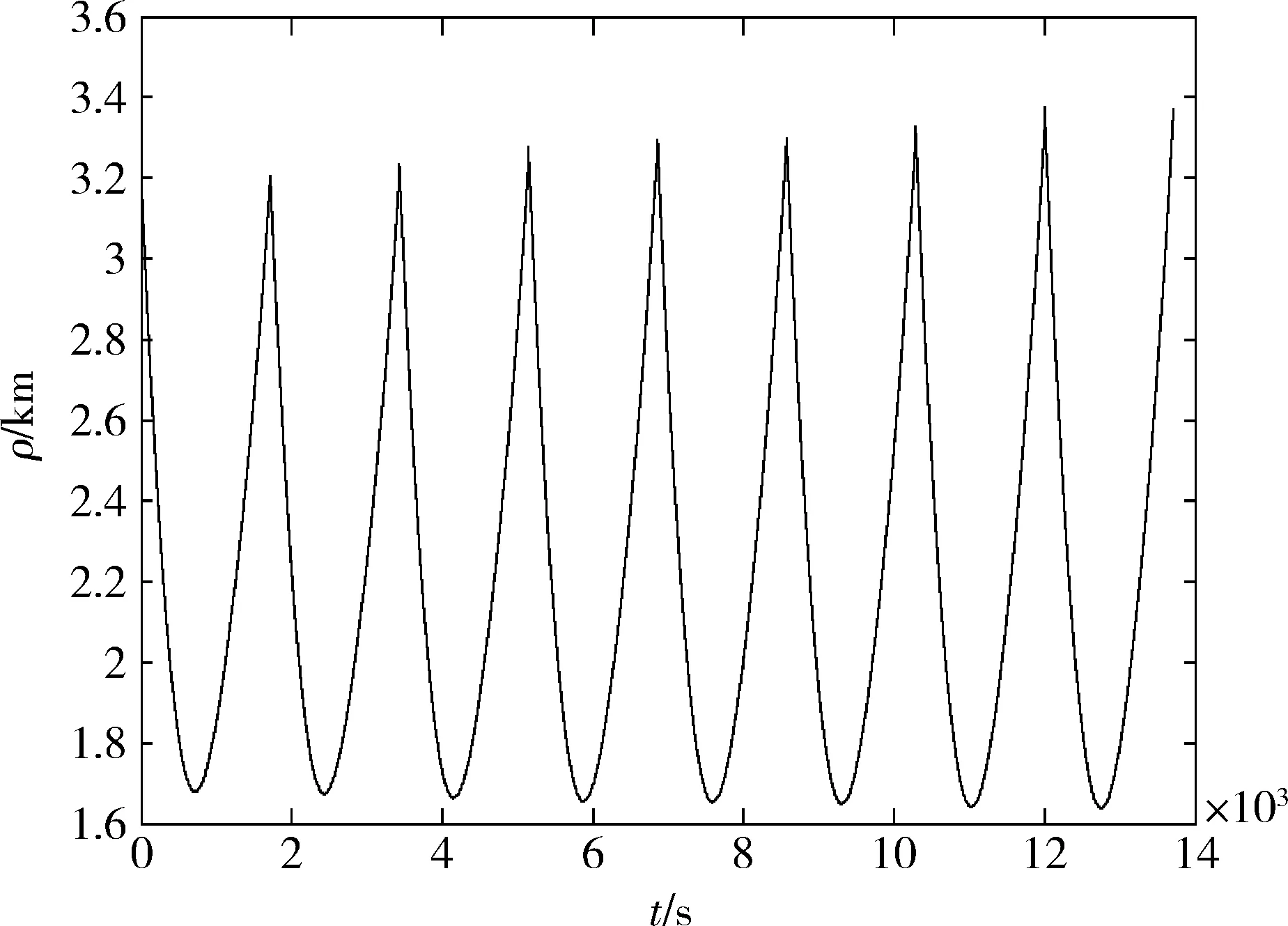
图3 脉冲悬停相对距离

由图3可以看出，随着脉冲悬停的持续，轨道机动初始和终止时刻2个航天器的相对距离逐渐变化，即悬停位置的实际值相对理论值出现了偏差，这是由于本文给出的航天器相对悬停方法的动力学模型略去了二阶及二阶以上的高阶小量，存在一定的模型误差。同时，2个航天器相对距离的最小值也在发生变化。图3显示本算例的相对距离最小值逐渐减小，这一变化理论上可使相对悬停过程中2个航天器发生碰撞的可能性逐渐增大。

图4 脉冲悬停的碰撞概率

图4给出了2个航天器相对悬停过程中，碰撞概率的变化情况。可以看出相对悬停的每一次轨道机动过程中，2个航天器碰撞的概率都是先增大后减小，且碰撞概率的极值点逐渐增大。对比图3可知，碰撞概率的极值点与2个航天器相对距离的最小值几乎同时出现。这说明，随着悬停点的“漂移”，相对悬停的2个航天器的相对距离也随之逐渐变化，如果相对距离逐渐减小，则2个航天器发射碰撞的可能性将逐渐增大。

在进行空间相对悬停任务的工程设计时，可以预先设定一个碰撞概率的阈值，应用本文给出的悬停轨迹安全分析方法对悬停轨道机动的碰撞概率进行预估，当该预估值小于设定的阈值时，说明本次轨道机动不太可能造成2个航天器的碰撞，可以正常实施轨道机动。反之，当预估值大于设定的阈值时，则说明本次轨道机动有较大可能会造成2个航天器的碰撞，应立即进行悬停点修正，适当增加2个航天器的最小相对距离，降低碰撞发生的可能性。

5 结论

基于航天器相对运动C-W方程的解析解，给出了航天器相对悬停的脉冲方法，实现了脉冲推力作用下的圆或近圆参考轨道的空间相对悬停控制，利于采用技术成熟的大推力轨控发动机实现对航天器空间相对悬停的控制。基于碰撞概率的思想给出了空间相对悬停运动的轨迹安全分析方法，建立了悬停相对运动碰撞概率密度计算模型，并在航天器结构球形包络及总包络球内的概率密度均匀的条件下给出了相对悬停运动的碰撞概率计算方法，对悬停的碰撞风险进行了量化，分析结果相对更加客观和可信。

数值仿真分析结果显示，在一定悬停精度条件下，本文方法可实现圆或近圆参考轨道上主动航天器相对目标航天器的空间相对悬停，且悬停轨道机动的周期越短，相对悬停越稳定。每个周期的悬停相对运动过程中，2个航天器碰撞的概率先增大后减小。悬停碰撞概率的极值点与2个航天器相对距离的最小值几乎同时出现。

[1] 陈小前，袁建平，姚雯，等. 航天器在轨服务技术[M]. 北京：中国宇航出版社，2009：1-22.

[2] 袁建平，李俊峰，和兴锁，等. 航天器相对运动轨道动力学[M]. 北京：中国宇航出版社，2013：482-561.

[3] 潘屹. 航天器相对运动水滴型悬停轨道研究[J]. 航天器工程，2014，23(4)：13-18.(PanYi.StudyonSpacecraftRelativeDrip-dropHoveringOrbit[J].SpacecraftEngineering, 2014，23(4)：13-18).

[4] 饶殷睿，韩潮，殷建丰，等. 航天器悬停构型设计与控制方法[J]. 航空学报，2015，36(7)：2361-2371.(RaoYinrui,HanChao,YinJianfeng,etal.MethodofSpacecraftHoveringFormationDesignandControl[J] .ActaAeronauticaetAstronauticaSinica, 2015，36(7)：2361-2371.)

[5]PateraRP.SatelliteCollisionProbabilityforNon-linearRelativeMotion[C]//AIAA/AASAstrodynamicsSpecialistConferenceandExhibit.Monterey：AIAA，2002：1-11.

[6] 王华，唐国金，李海阳. 基于碰撞概率的交会对接近距离导引段的轨迹安全[J].宇航学报，2007, 28(3)：648-652.(WangHua,TangGuojin,LiHaiyang.CollisionProbabilityBasedTrajectorySafetyinCloseRangeGuidancePhaseofRendezvousandDocking[J].JournalofAstronautics, 2007，28(3)：648-652.)

[7]XuXL,XiongYQ.AnalysisoftheApplicabilityofCollisionProbabilityAlgorithmsforNonlinearRelativeMotion[J].ScienceChina,Physics,Mechanics&Astronomy, 2013，56(5)：1041-1046.

[8] 刘暾, 赵均. 空间飞行器动力学[M]. 哈尔滨：哈尔滨工业大学出版社，2003：83-101.

[9]ClohessyWH,WiltshireRS.TerminalGuidanceSystemforSatelliteRendezvous[J].JournaloftheAerospaceScience, 1960，27(9)：653-658.

[10]LovellTA,TragesserSG.GuidanceforRelativeMotionofLowEarthOrbitSpacecraftBasedonRelativeOrbitElements[C]//AIAA/AASAstrodynamicsSpecialistConferenceandExhibit.Providence：AIAA，2004：1-15.

[11] 张爱萍. 可逆矩阵的判定及求法[J]. 赤峰学院学报，2011，27(3)：12-13.

[12] 杨保华. 航天器制导、导航与控制[M]. 北京：中国科学技术出版社，2011：51-95.

[13]GottliebRG,SponaugleSJ,GaylorDE.OrbitDeterminationAccuracyRequirementforCollisionAvoidance[C]//AIAA/AASSpaceFlightMechanicsMeeting.SantaBarbara：AIAA，2001：1105-1121.

[14] 曹莉，文海玉. 应用数理统计[M]. 哈尔滨：哈尔滨工业大学出版社，2012：165-208.

[15] 朱建平. 应用多元统计分析[M]. 北京：科学出版社，2012:8-26.

Methods of Spacecraft Impulse Relative Hovering in Near Circular Orbit and Trajectory Security Analysis

Cheng Bo1,2,3, Yuan Jianping1,3, Qian Yingjing4, Ma Weihua1,3

1. Northwestern Polytechnical University, Xi’an 710072, China2. Beijing Institute of Astronautical Systems Engineering, Beijing 100076, China3. National Key Laboratory of Aerospace Flight Dynamics, Xi’an 710072, China4. Beijing University of Technology, Beijing 100124, China

BasedontheC-Wequationsanditsanalyticalsolutions,thespacecraftimpulserelativehoveringhasbeenstudied.Acomputationmethodoforbit-transfervelocityincrementforhoveringispresented,whichismoreadaptiveforthespacecraftenginesystem.Basedonthecalculationmethodofrelativemotioncollisionprobability,thehoveringtrajectorysecurityisanalyzed.Thenumericalsimulationsshowthattheintroducedimpulsehoveringmethodinthispaperisfeasibleandtheorbittransferperiodreductioncanimprovethehoveringperformance.Themaximalcollisionprobabilityduringrelativehoveringandtheminimumdistancebetweenthetwospacecraftscanalmostappearatthesametime.

Nearcircularorbit;Relativehovering;Impulse;Collisionprobability;Trajectorysecurity

2016-10-14

程 博(1983-)，男，陕西人，博士研究生，工程师，主要研究方向为航天器动力学与控制；袁建平(1957-)，男，陕西人，博士生导师，教授，主要研究方向为飞行器设计，航天飞行动力学与控制；钱霙婧(1984-)，女，安徽人，博士，讲师，主要研究方向为平动点动力学与控制，自主导航研究；马卫华(1978-)，男，河南人，博士，副教授，主要研究方向为飞行动力学和组合导航。

V412.4

A

1006-3242(2017)01-0013-07