遗传算法在故障安全控制系统多故障中的应用

董永武

英国索尔福德大学，英国 索尔福德



遗传算法在故障安全控制系统多故障中的应用

董永武

英国索尔福德大学，英国 索尔福德

着重于故障安全控制系统在单个以及多个调节器故障情况下，使系统仍然保持稳定以及拥有良好的系统性能。因此,多变量故障安全控制系统是设计重点。进化计算技术(Evolutionary Computing Techniques)改变了控制系统设计原理。相比使用传统的办法比如伪逆(Pseudo inverse)设计方案，进化算法(Evolutionally Algorithm)能更好的优化设计系统,其用成本函数(Cost Function)和最优化(Optimization)进化出结果。在进化算法里，有多种系统性能指标优化系统性能，比如积分平方差算子(Integral Squared Error Operator)就用作成本函数来设计控制器。本文着重运用遗传算法优化这种控制系统的控制器，使这种控制系统的性能随运算时间的增加而变好。

遗传算法； 故障安全控制系统； 非方控制系统

安全性和可靠性是设计多变量系统控制器以及复杂的工业系统的重要目标之一，也是重要的设计规范之一，是多变量系统设计领域的一个重要研究领域。故障安全系统的逻辑系统由Mine H和Koga Y研发，目的是保证系统输出在包括有调节器失效的情况下，仍然保持稳定。

现有很多被动式设计方法可以保证系统的稳定性以及可以接受的系统性能，但不是最优的系统性能。比如Fripp应用伪逆方法(Pseudo inverse method)设计了在单个调节器失效情况下的多变量控制系统的控制器[1]。Veillette R J, Medanic J V和Perkins W R设计了集中以及分散控制设计方法，保证系统在没有调节器失效以及有单个调解器失效情况下的稳定性以及系统的H无穷性能[2]。Zhao Q和Jiang J更新了鲁棒法(Robust method)，以保证系统在没有调节器失效以及有单个调解器失效情况下的稳定性以及可以接受的系统性能[3]。Yang G H, Wang J L, Soh Y C和Liao F发展了可靠控制设计方法(reliable control design method)，设计出一个不变的控制器来保证系统的稳定性以及H无穷性能[4]。

遗传算法是另一种可以用来设计这种控制器的方法[5]，它可以用来设计控制器以保证系统在没有调节器失效以及有调解器失效情况下的稳定性以及最优系统性能。

本文使用单成本函数以及多成本函数遗传算法最优化故障安全多变量控制系统。多变量控制系统的性能测量为设定点追踪性能加上交互性能，并用积分平方差计算为成本函数。

1 故障安全系统的设计

1.1 单目标的遗传算法设计多变量控制系统

单目标的遗传算法是标准的遗传算法，使用了进化的概念，比如用大小选择(selection) 、组合交叉(crossover)和变异(mutation)产生新的解集，优化并寻找答案。第一个使用遗传算法的是Holland J H[6]。标准的遗传算法还包括基于个体适应度(individual fitness)的大小选择过程，个体适应度用成本函数计算， 并使用组合交叉以及变异来产生新的解集。

1.2 多目标的遗传算法设计多变量控制系统

实际上不止一个变量需要最优化，有时需要多个变量同时最优化。单成本函数的遗传算法可以添加权重因数(weighting factor)，但是权重因数非常难选择，因此研发出多成本函数的遗传算法[7]。再加上许多现实问题多组最优答案，这些解集被更广义的最优化。在所有条件下，没有一个最优解比其他最优解更优异，这就是Pareto最优解(non-dominated Pareto-optimal solutions[8])。

1.3 遗传算法设计方法

Fripp R N的设计方法只保证系统在没有调节器失效以及单个调节器失效情况下的稳定性，但是不保证系统的最优性能。相比Fripp R N的被动式设计方法，遗传算法可以用来设计并最优化控制器的参数。

用遗传算法通过成本函数找到最优解，成本函数选择仍然是测量控制系统的性能。系统性能通过测量系统在不同的控制条件以及在不同的控制器下的性能。

成本函数是所有没有调节器失效和有调节器失效情况下的积分平方差的和。

每一个单独计算为:

ISEt=∑ISEi,j,k

其中，t是失效的调节器号码。t=0 就是没有调节器失效;t=1表示调节器1号失效；t=2表示调节器2号失效；i是失效的调节器号码；j是改变的设定点的编号；k是输出的号码。

因此，单独成本函数遗传算法的成本函数计算为:

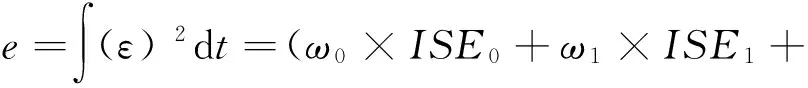
对于单独成本函数遗传算法，有2种成本函数计算方法。第1种是全局优化(Global Optimisation)，就是把所有情况下的设定点追踪积分平方差和交互积分平方差相加[9]。在这种计算方式下，遗传算法会把所有积分平方差的和最小化。第2种是最差失效状态最优化(Worst Case Failure Optimisation)，就是把设定点追踪积分平方差和交互积分平方差的和的最大值最优化。在这种计算方式下，遗传算法设计出控制器把最大的积分平方差最小化。

多目标遗传算法是把单独的失效情况单独最优化。这种优化方式是没有调节器失效与其他所有失效情况之间的权衡。多目标遗传算法会用Pareto最优方法找到一个解集，同时最优没有调解器失效与有调节器失效的所有情况。

1.4 遗传算法设计单独调节器和多个调节器失效下的故障安全控制系统

因为Fripp的方法只保证单独调节器失效情况下系统的稳定性，遗传算法却可以寻找到单个调节器和多个调节器失效情况下的最优控制器，因此这个例子包含多个调节器失效的情况。

下式是一个4输入2输出的多变量故障安全控制系统，开环转换函数表示为：

因为这个系统的输入数量比输出数量多2个，因此，系统可以在1个或者2个调节器失效的情况下保持稳定。如果将所有1个和2个调节器失效的情况都考虑进来，就有11个不同的情况和11个单独的ISEi。

使用2个设计方式： 1)Fripp R N的伪逆方法 (1988), 遗传算法找到对角线调整矩阵来优化控制器； 2)遗传算法直接选择所有控制器的所有变量，虽不能保证一定会找到所谓的最优解，但可以进化出设计好的问题的最优解。

在伪逆法里，成本函数是全局最优。在纯遗传算法设计方法中，分别测试全局最优和最差失效状态最优化。

1.5 伪逆设计方法设计全参数最优

通过Fripp R N的设计方法，得出比例和积分控制器参数为：

然后通过单目标的遗传算法,用全局最优成本函数，找到Δ1=4.9569,Δ2=5.6069,Σ1=6.1587 andΣ2=12.7458。

因此，伪逆算法最终的最优控制器参数为：

遗传算法设计控制器参数并包含过载限定。同样的，系统的比例和积分控制器表述为：

因此，kp11,kp12,kp21,kp22,kp31,kp32,kp41,kp42,ki11,ki12,ki21,ki22,ki31,ki32,ki41和ki42是需要遗传算法寻找的16个参数。使用全局最优成本函数的遗传算法选择的比例和积分控制器为:

这次遗传算法使用最差失效状态最优化成本函数，选择控制器参数。因此,遗传算法选择的比例和积分控制器为:

。

1.6Pareto最优设计单个和多个调节器失效故障安全控制系统

因为单成本函数遗传算法的权重因数α等于1,但是在现实生活中，权重因数不一定一直是1，它会随情况的改变而改变。

相对于单目标遗传算法，多目标遗传算法可以同时优化每一个单独的子设定，因此就不需要选择权重因子。所以不需要找到独立的最优解，取而代之的是Pareto最优解集。在该方法驱动下，每一个子设定都会在不影响其他子设定的情况下最优化。因此每一代都只有这种最优解被保留。

表1 三种设计方案的积分平方差对比

图1 伪逆设计和遗传算法设计ISE对比

本节使用同样的4输入2输出例子。kp11,kp12,kp21,kp22,kp31,kp32,kp41,kp42,ki11,ki12,ki21,ki22,ki31,ki32,ki41和ki42是需要多目标遗传算法优化的16个参数。

使用Pareto最优方法后，没有调节器失效、单个调节器失效和多个调节器失效的情况下的积分平方差同时得到最优化，如表1所示每一个积分平方差都包含设定点追踪和交互。

2 结论

遗传算法成功地设计了故障安全系统，可以进化出控制器，保证系统无论在有无调节器失效的情况下都有良好的系统性能。用遗传算法达成进化控制器全参数的目标。如表1所示，与伪逆算法相比，单目标遗传算法提升系统性能99%。

用单目标遗传算法可以让ISE和最优。但是单独的ISE可能不是最优。如表1所示，ISE和是99.85，与伪逆算法相比缩小很多，但是在调节器3和4失效的情况下，ISE是27，仍比其他情况大。

运用最差失效状态成本函数，最差失效情况下的ISE最优，全局就不能最优。如表1所示，在调节器3和4失效的情况下ISE是25，比全局最优情况下小，但是ISE和与全局最优比是145。

多目标遗传算法用来找到最优解集。最优解集包含了全局最优，如表2所示，ISE和104与单目标遗传算法的99.85很接近。最优解集包含了很多有用的设计，如表2里每一列的最小值所展现的，每次多目标遗传算法运行，都包含了不止一个最优设计，因此多目标遗传算法是一个非常有效的设计工具。如表2所示，多目标遗传算法进化出了最优解集。

根据上述结论，建议如下:

1) 用伪逆算法算出控制器参数，以此作为遗传算法的开始节点。保证遗传算法能有更好的机会进化出更好的结果；

2) 用全局最优解决ISE和的最优。如果想找到最差失效情况下的最优性能就用最差失效状态最优；

3) 如果设计者知道权重因数，就用单目标遗传算法找到单个最优结果；

4) 如果设计者需要知道所有最优组合，就用多目标遗传算法找到最优解集。如表2所示，设计者可以选取任何组合的最优解。

表2 故障安全系统的Pareto最优结果

[1] Fripp R N. Design of Digital Controllers for Multivariable Plants with Actuator Failures[M]. The University of Salford, (1988).

[2] Veillette R J, Medanic J V, Perkins W R. Design of Reliable Control Systems[J]. IEEE Transactions on Automatic Control. 1992,37(3):290-304.

[3] Zhao Q, Jiang J. Reliable State Feedback Control System Design Against Actuator Failures[J]. Automatica, 1998,34(10), 1267-1272.

[4] Yang G H, Wang J L, Soh Y C. ReliableH∞ControllerDesignforLinearSystem[J].Automatica, 2001,37(5):717-725.

[5]PorterB,JoneAH.GeneticTuningofDigitalPIDControllers[J].ElectronicsLetter, 1992,28:843-844.

[6]HollandJH.AdaptationinNaturalandArtificialSystems[M].ReprintEdition,MITPress;Cambridge,Massachusetts(UnitedStates), 1992.

[7]IshibuchiH,OsakaPrefectureUnivOsak,NojimaYusuke,DoiT.ComparisonbetweenSingle-ObjectiveandMulti-ObjectiveGeneticAlgorithms:PerformanceComparisonandPerformanceMeasures[C].EvolutionaryComputation,CEC2006.IEEECongresson, 2006.

[8]WeileDS,MichiellsenE,GoldbergDE.GeneticAlgorithmDesignofParetoOptimalBroadbandMicrowaveAbsorbers[J].IEEETransactionsonElectromagneticCompatibility, 1996,38(3):518-525.

[9] Solihin M I, Wahyudi, Kamal M A S, Legowo A. Objective Function Selection of GA-Based PID Control Optimization For Automatic Gantry Crane[C]. Computer and Communication Engineering, International Conference on, 2008: 883-887. ICCCE 2008.

[10] Coit D W, Jin T, Wattanapongsakorn N. System Optimization With Component Reliability Estimation Uncertainty: A Multi-Criteria Approach[J]. IEEE Transcations on Reliability, 2004,53(3).

[11] Chakraborty A. Fault Tolerant Fail Safe System for Railway Signalling[C]. Proceedings of the World Congress on Engineering and Computer Science 2009 Vol II WCECS 2009, San Francisco, USA, October 20-22, 2009.

Genetic Design of Multivariable Fail-safe Control System

Dong Yongwu

The University of Salford, The Crescent, Salford, M5 4WT

Inthisthesisthedesignofmultivariablefail-safecontrolundersingleandmultiplefailuresareconsidered,thegoalofthisthesisismakingsurethefail-safecontrolsystemremainstableandoptimalperformancesimultaneously.Theinventionofevolutionarycomputingtechniqueshaschangedthedesignphilosophyforcontrolsystemdesign.Suchalgorithmsevolvesolutionsusingcostfunctionsandoptimization.Thereareavarietyofsystemperformanceindicatorssuchasintegralsquarederroroperatorhasbeenusedascostfunctionstodesigncontrollersusingsuchalgorithms.Therefore,themainobjectiveofthisthesisistousethegeneticalgorithmstoinvolvefail-safemultivariablecontrollers,suchthattheyperformwellinthetime-domain.

GeneticAlgorithm;FailSafeControl;Non-squaresystem

2016-11-29

董永武(1986-),男，重庆人，博士研究生，主要研究方向为飞行控制、遗传算法。

TP316.2

A

1006-3242(2017)01-0008-05