基于伺服机构饱和抑制的模糊滑模控制方法

刘海东 包为民李惠峰

1.北京航空航天大学宇航学院，北京 1001912.空间物理重点实验室, 北京 100076



基于伺服机构饱和抑制的模糊滑模控制方法

刘海东1,2包为民1,2李惠峰1

1.北京航空航天大学宇航学院，北京 1001912.空间物理重点实验室, 北京 100076

以高超声速飞行器为研究对象，设计了一种模糊变增益滑模姿态控制器。在控制器的设计中，应用动态逆方法对控制对象的俯仰、偏航和滚转通道进行解耦处理。通过滑模变结构控制方法保证被控系统的鲁棒特性。为了抑制伺服机构饱和，基于专家控制经验设计了滑模控制器增益模糊控制规则。通过仿真验证，证明了本文设计的控制方法在高超声速飞行器姿态控制和伺服机构饱和抑制两方面的有效性。

高超声速；动态逆；滑模控制；模糊；饱和抑制

高超声速飞行器一般是指飞行马赫数大于5的飞行器，其飞行空域主要为距地面20km～100km的临近空间。在高超声速飞行条件下，飞行器周围流场将呈现高超声速气体流动学特有的特征，即薄激波层、黏性干扰、熵层、高温效应和低密度效应[1]。由于飞行速度快、飞行包线大、飞行环境复杂且难于准确预测，近年来高超声速飞行器控制问题一直是控制领域的研究热点。

高超声速飞行器动力学具有强耦合、强非线性和不确定性等特性，单一控制方法难以在其控制中达到良好效果，因此,研究高超声速飞行器控制问题需要综合运用控制方法开展控制器设计。其中，比较典型的策略是综合应用动态逆和滑模变结构控制的方法[2-3]。其中，动态逆主要用于解决高超声速飞行器各个控制输入量与输出量之间的耦合问题，滑模变结构控制方法主要用于保证系统鲁棒[4]。另外，由于高超声速飞行器飞行包线大，固定增益控制器难以适应全程需求，因此，需要在飞行过程中动态调整增益，其中比较典型的方法包括自适应控制[2]、模糊控制[5]和神经网络[6]等。崔亚龙基于模糊控制研究了滑模控制器边界层的自适应调整。伺服机构的饱和问题在传统研究中相对关注较少。

本文综合应用动态逆和滑模控制实现对被控对象的姿态控制。同时，基于模糊控制策略动态调整控制器增益参数。

1 运动模型

在建模时假设飞行器的惯量积远小于转动惯量，并忽略飞行器的速度、位置变化情况及地球自转角速度对飞行姿态的影响。基于上述假设，在飞行器坐标系下建立高超声速飞行器姿态运动简化模型，可描述为

(1)

式中，ωx，ωy，ωz分别表示滚动角速度、偏航角速度和俯仰角速度；φ，ψ，γ分别表示俯仰角、偏航角和滚动角；Mx，My，Mz分别表示滚动力矩、偏航力矩和俯仰力矩；Jx，Jy，Jz分别表示x轴、y轴和z轴3个方向的转动惯量。

本文选用NASA兰利研究中心具有轴对称锥形体外形的高超声速飞行器动力学模型[7]。力矩计算表达式如下

(2)

其中，q=0.5ρv2表示动压，S表示参考面积，b表示侧向参考长度，c表示纵向参考长度，mx，my，mz分别表示滚动力矩系数、偏航力矩系数和俯仰力矩系数。气动力矩系数表达式由Keshmiri等人基于CFD 计算数据和风洞测试数据采用多项式拟合方法得到[8-9]：

(3)

其中，各项系数均表示为马赫数M、攻角α、侧滑角β、左升降舵偏角δe、右升降舵偏角δa和方向舵偏角δr的五阶多项式函数。在不同马赫数范围内，系数表达式不同。

2 控制器设计

2.1 逆系统环节设计

将表达式(1)表示为

(4)

其中，Θ=[φψγ]T，ω=[ωxωyωz]T，J=diag[JxJyJz]，UM=[MxMyMz]T，

(5)

(6)

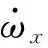
(7)

(8)

将式(4)中第2式代入式(7)，可得

(9)

因此，逆系统环节设计为

(10)

其中，逆系统环节的输入为俯仰角、偏航角和滚动角二阶导数的期望值，输出为期望的控制力矩。

2.2 滑模控制器设计

首先，将滑模控制器的滑模面设计为

(11)

其中，ai(i=φ,ψ,γ)为正实数。其次，设计基于饱和函数的指数趋近律如下

(12)

其中，εi和ki(i=φ,ψ,γ)均为正实数，sat(.)为饱和函数，其中Δ为边界层厚度。

(13)

对式(11)进行求导，联立式(12)，可得

(14)

其中

(15)

(16)

基于上述推导，可得

(17)

因此，控制器实际输出的控制力矩Uc可以表示为

(18)

2.3 模糊控制器设计

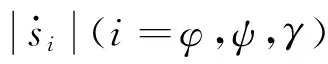
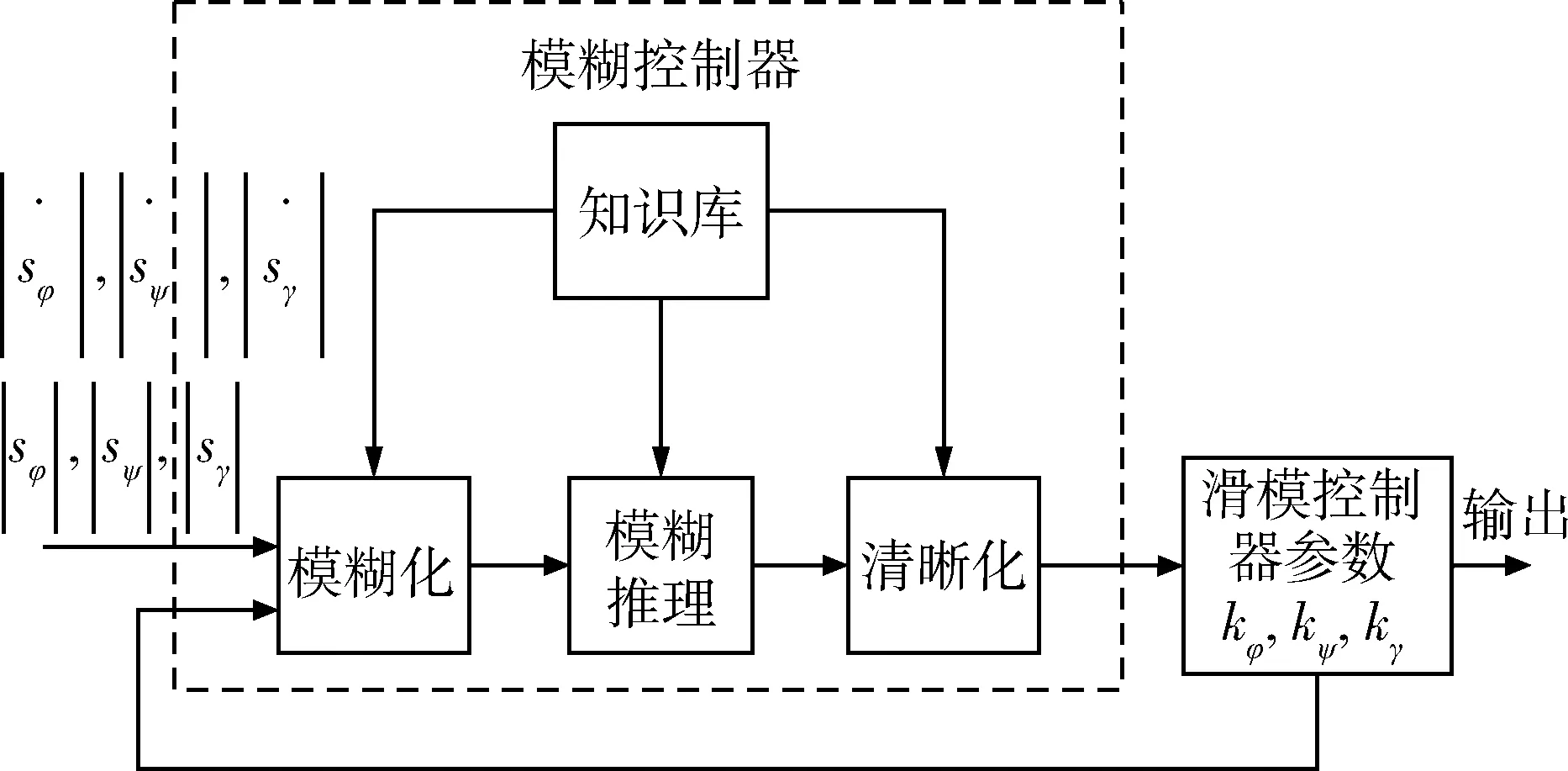
图1 模糊控制器组成逻辑

(1)定义模糊集合如表1所示。

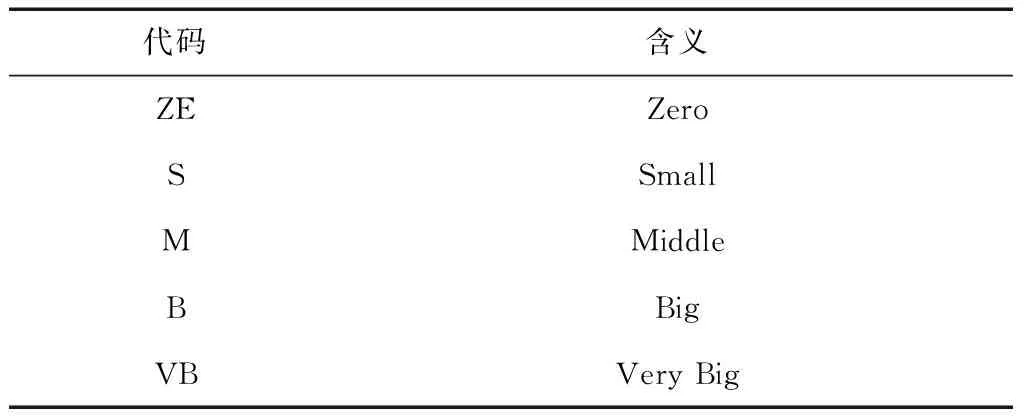
表1 模糊集合定义

(2)模糊化和模糊规则定义。

A={S,M,B}， B={S,M,B} ，
C={ZE,S,M,B,VB}。

根据控制经验，提出如下控制规则：

1)当系统状态距离滑模面较远时，应选择较小控制器增益，防止因控制能力需求过大而导致伺服机构饱和；

2)当系统状态距离滑模面较近时，应选择较大控制器增益，以提升控制效率和系统鲁棒性；

3)当滑模面函数变化快时，适当减小增益；

4)当滑模面函数变化慢时，适当增大增益。

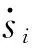
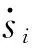
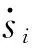
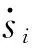
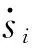
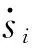
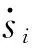
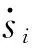
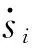
(3)隶属度函数描述

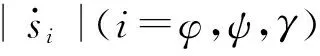
(19)

对于输出变量，采用单点模糊集合进行描述。

一把吉他，轻抚，一腔心思便如春天的气息，在优美的乐声里生发出来。弹指一挥间，鄌郚的琴声，穿过世界间的距离，直通人心……

(4)模糊推理与清晰化

本文设计的模糊规则为两输入单输出形式，单一控制规则表示为

Ri=(AiandBi)→Ci

(20)

全部模糊控制规则的总蕴含关系表示为

(21)

假设输入量为：x是A′andy是B′，根据模糊控制规则进行模糊推理，可以推出模糊量z(用模糊集合C′表示)为

C′=(A′ andB′)°R

(22)

其中，“and”运算采用求交，合成运算“。”采用最大～最小方法。

在清晰化方面，采用加权平均法来进行模糊量的清晰化。

3 仿真验证

NASA兰利研究中心(LangleyResearchCenter)具有轴对称锥形体外形的高超声速飞行器动力学模型的主要模型参数见表2。

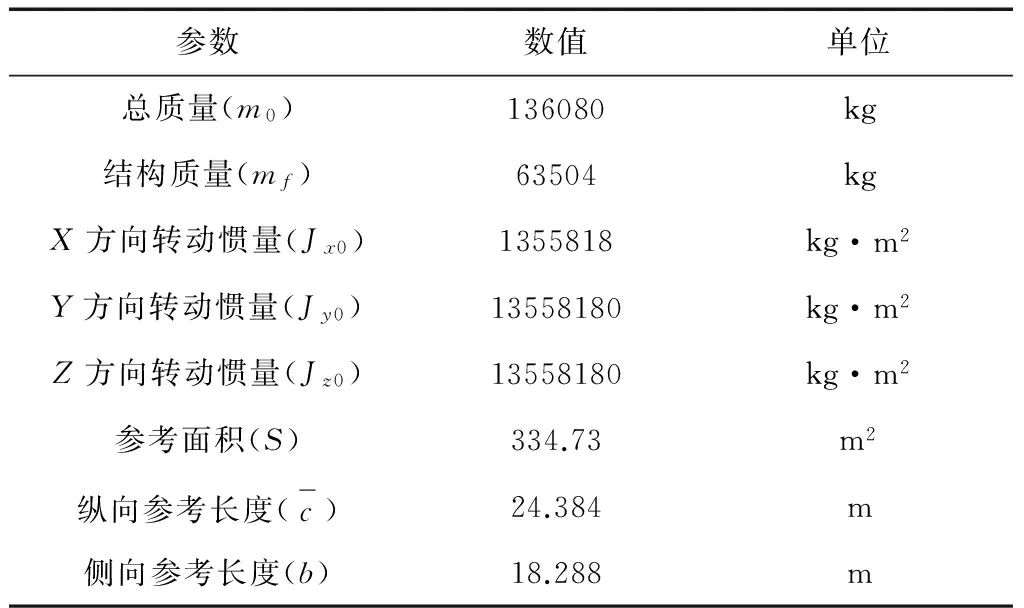
表2 模型主要参数

仿真初始条件为φ=1.79°，ψ=4°，γ=-5°，v0=4590.3m/s，h=33528m，ωx=ωy=ωz=0(°)/s。姿态控制指令为φd=12°，ψd=0°，γd=0°。飞行器模型升降舵和方向舵的舵偏角范围为(-30°，30°)。控制器参数设置如下a1=a2=a3=1，ε1=ε2=ε3=1，Δ1=Δ2=Δ3=1，不同模糊集合下ki(i=φ,ψ,γ)取值参见表3。仿真中，假设外部干扰为表达式(23)，气动参数(mx,my,mz)偏差为20%。

表3 参数ki取值

(23)

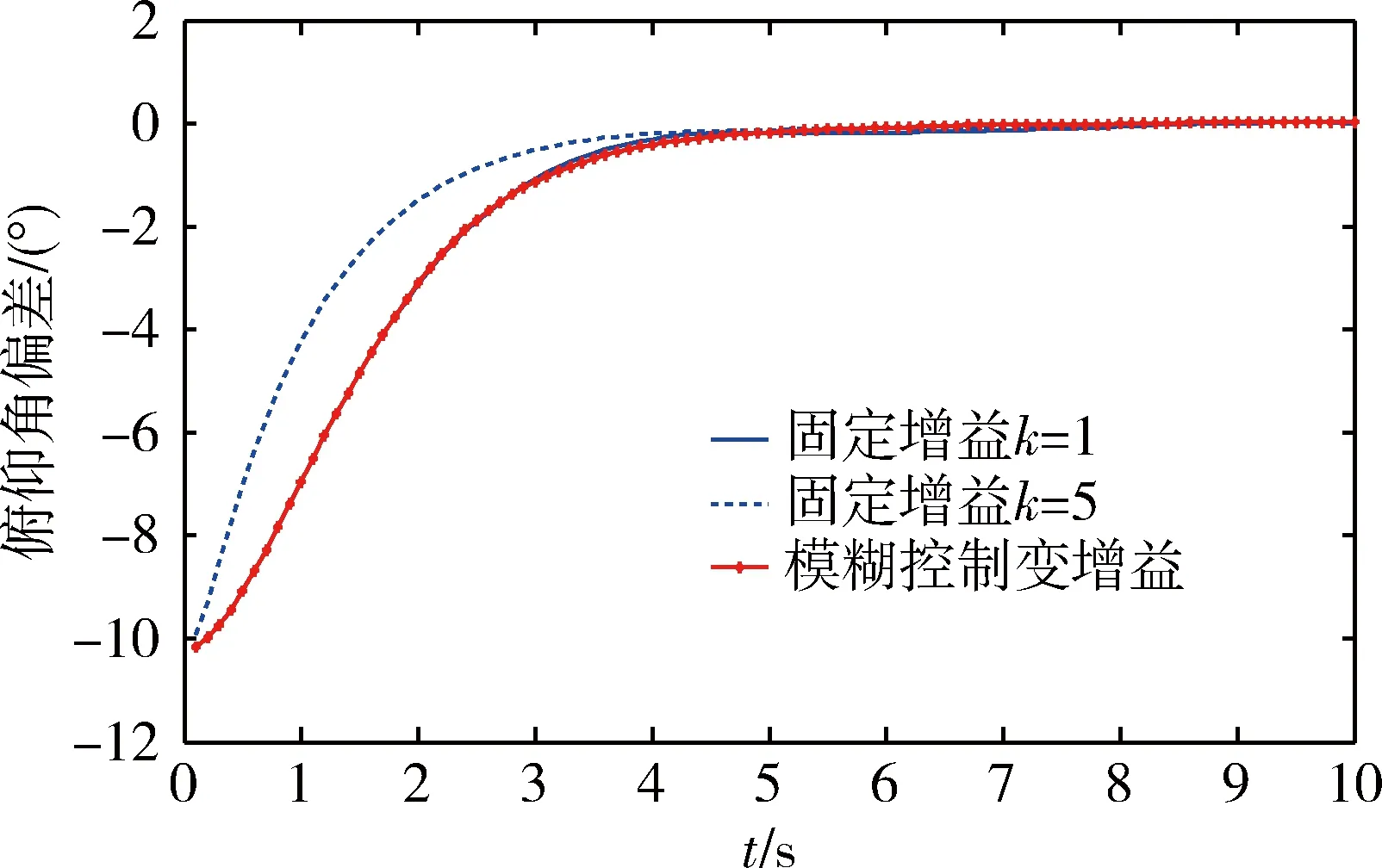
图2 俯仰角偏差对比

分别将参数k设定为固定值1和5，应用模糊控制法动态调整k值，开展3次仿真。仿真结果如图2～7所示，其中图2～4表示存在模型不确定性和外部干扰的情况下，飞行器实际姿态角与期望值的偏差情况。图5～7表示姿态控制过程中，升降舵和方向舵的变化情况。通过仿真结果分析，不难发现，对于固定增益滑模控制方法，当选择较低增益时，可能导致鲁棒性不足，难以有效抑制外部干扰；当选择较高增益时，虽然能提高系统鲁棒性和姿态调整速率，但是却可能导致伺服机构负担过重，严重情况下甚至可能造成伺服机构饱和。由此可见，应用固定增益的滑模变结构控制方法存在其局限性。相比而言，基于模糊控制策略的变增益滑模变结构控制方法，既能保证系统的鲁棒性和控制效率，又能使伺服机构平稳变化，防止饱和情况发生。

图3 偏航角偏差对比

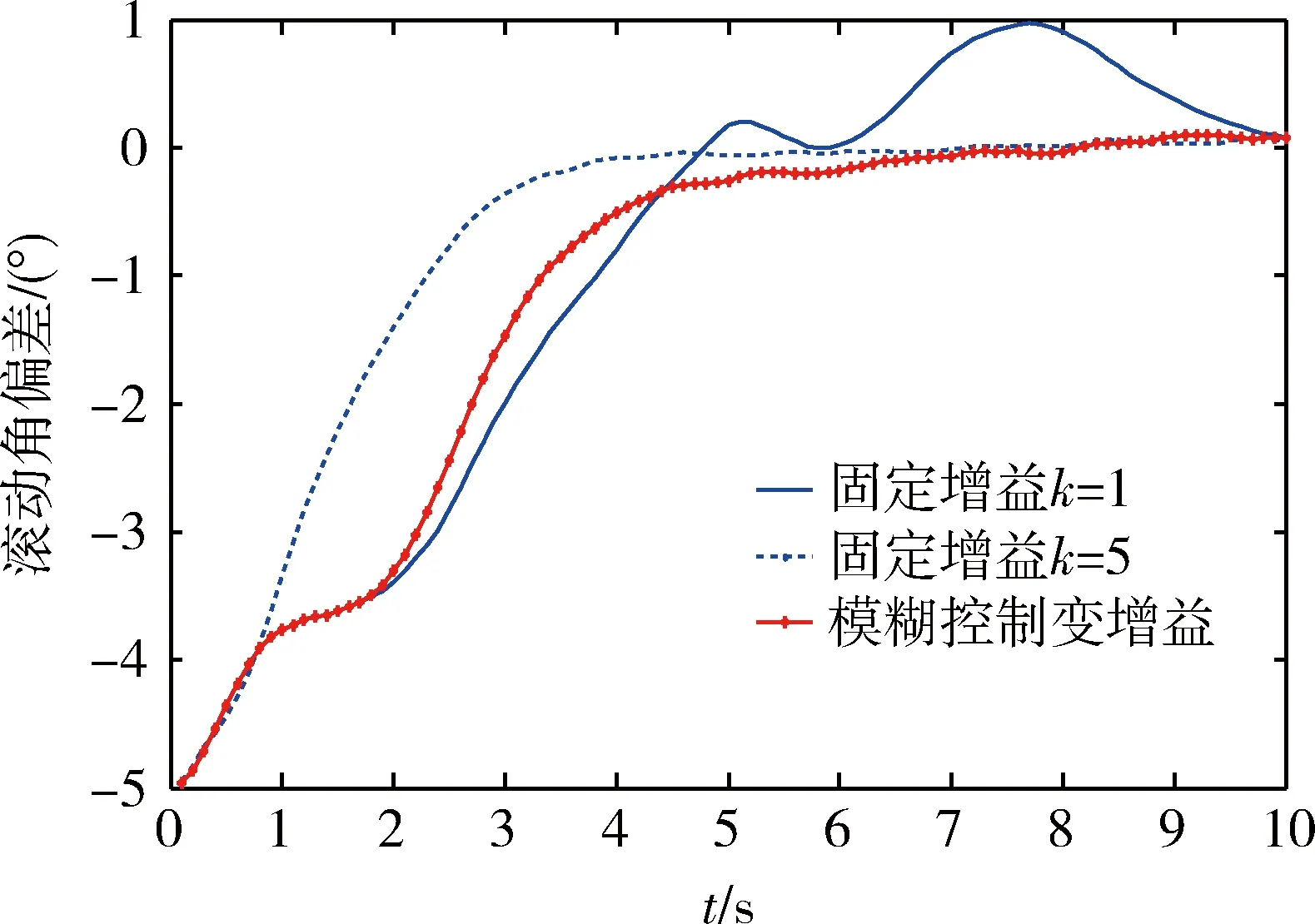
图4 滚动角偏差对比

图5 右升降舵偏角变化过程

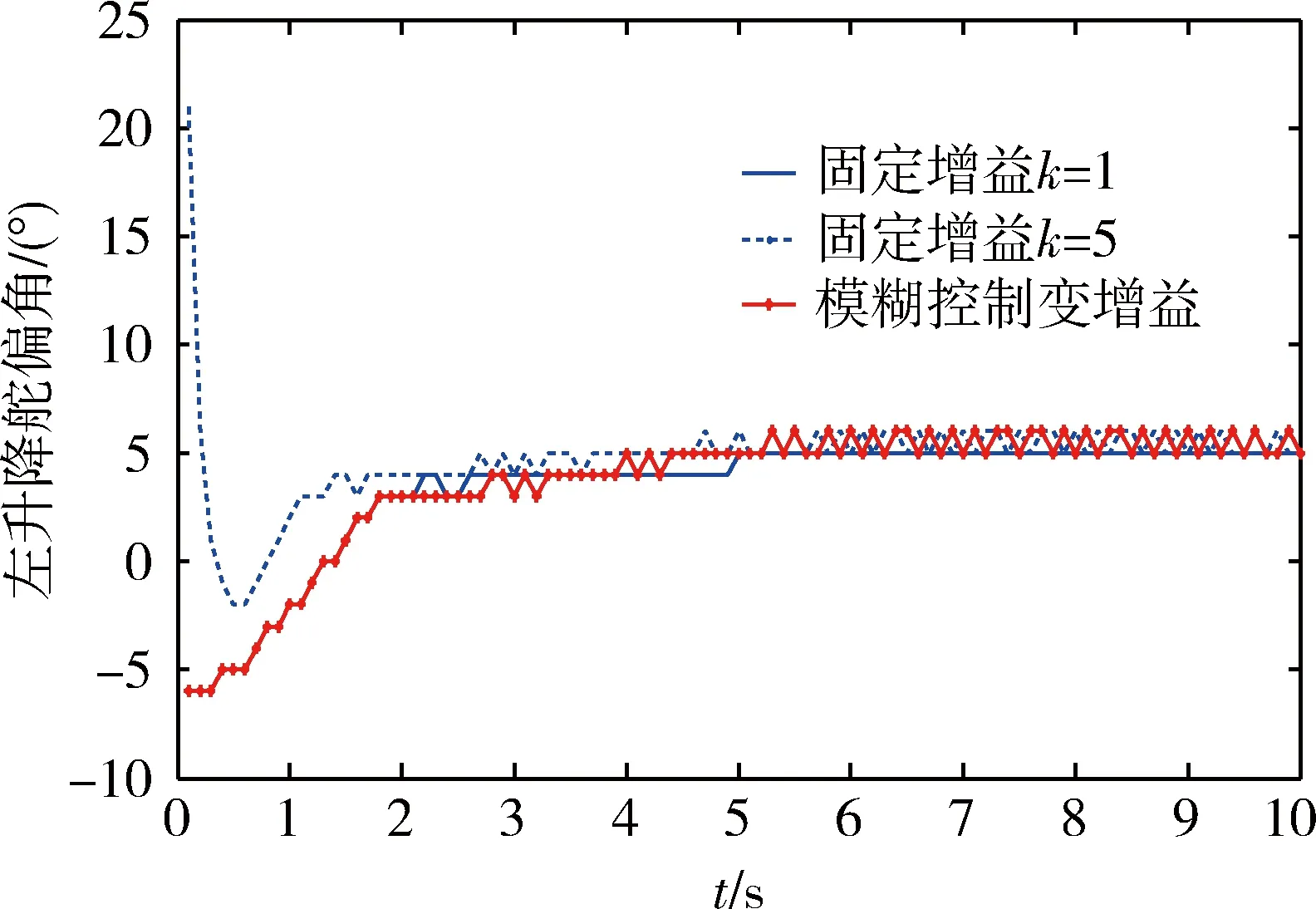
图6 左升降舵偏角变化过程

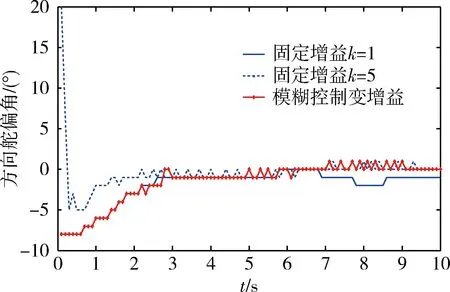
图7 方向舵偏角变化过程

4 结论

以高超声速飞行器作为研究对象，针对姿态控制问题，提出了一种基于模糊控制策略的变增益滑模变结构控制方法。经过仿真验证：

1) 在考虑模型不确定性和外部干扰的情况下，所设计的滑模变结构姿态控制方法能保证控制指令的有效响应；

2) 所设计的模糊控制方法能基于系统状态有效动态调整控制器增益，既保证系统鲁棒性，又不对伺服系统产生过大执行负担；

3) 动态逆方法能对飞行器绕心动力学模型的多输入、多输出变量进行有效解耦。

在后续工作中，将进一步总结已有控制经验，应用模糊控制策略研究控制器其他参数的自使用控制策略，进而使姿态控制策略在整个高超声速飞行器飞行包线内具有有效性。

[1] 吴宏鑫,孟斌.高超声速飞行器控制研究综述[J].力学进展,2009,39(6):756-765.

(Wu Hongxin, Meng Bin. Review on the Control of Hypersonic Flight Vehicles[J]. Advances in Mechanics, 2009, 39(6): 756-765.)

[2] Xu J H, Maj D Mirmirani, Petros A Ioannou. Adaptive Sliding Mode Control Design for a Hypersonic Flight Vehicle[J].Journal of Guidance,Control,and Dynamics, 2004, 27(5): 829-838.

[3] Li H F, Sun W C,Li Z Y, Xue S B. Index Approach Law Based Sliding Control for A Hypersonic Aircraft[C]//U.S.Air Force T&E Days 2009. New Mexico:AIAA, 2009(AIAA 2009-1734).

[4] 刘金琨,孙富春.滑模变结构控制理论及其算法研究与进展[J].控制理论与应用, 2007, 24(3):407-418.(Liu Jinkun,Sun Fuchun.Research and Development on Theory and Algorithms of Sliding Mode Control[J].Control Theory & Applications,2007,24(3):407-418.)

[5] 崔亚龙,杨永浩,曹立佳,蔡光斌,张超.高超声速飞行器的滑模边界层模糊自适应控制方法研究[J].计算机测量与控制,2014,22(5):1426-1432.(Cui Yalong, Yang Yonghao, Cao Lijia, Cai G B, Zhang C. Research on an Adaptive Fuzzy Sliding Mode Boundary Layer Control Method for a Hypersonic Vehicle[J]. Computer Measurement & Control, 2014, 22(5): 1426-1432.)

[6] Xu J H, Maj D Mirmirani, Petros A Ioannou. Robust Neural Adaptive Control of a Hypersonic Aircraft[C]. AIAA Guidance, Navigation, and Control Conference and Exhibit, Austin, Texas:AIAA,2003(AIAA 2003-5641).

[7] Shaughnessy J D, Pinckney S Z, McMinn J D, et al. Hypersonic Vehicle Simulation Model: Winged-cone Configuration[R]. NASA Technical Memorandum 102610, 1990.

[8] Keshmiri S, Colgren R,Mirmirani M. Development of an Aerodynamic Database for a Generic Hypersonic Air Vehicle[C] //AIAA Guidance, Navigation, and Control Conference and Exhibit.San Francisco,California:AIAA,2005 (AIAA-2005-6257).

[9] Keshmiri S, Colgren R，Mirmirani M. Six DoF Nonlinear Equations of Motion for a Generic Hypersonic Vehicle [C]// AIAA Atmospheric Flight Mechanics Conference and Exhibit, Hilton Head, South Carolina:AIAA, 2007 (AIAA-2007-6626).

Fuzzy Sliding Mode Control Method Based on Saturation Restrain of Servo Mechanism

Liu Haidong1,2，Bao Weimin1,2， Li Huifeng1

1. School of Astronautics, Beihang University, Beijing 100191, China2. Science and Technology on Space Physics Laboratory, Beijing 100076, China

Thesixdegreesoffreedommodelofagenerichypersonicvehiclehavebeentakenastheresearchobjectinthispaper,andafuzzygain-schedulingslidingmodeattitudecontrollerisproposed.Inthedesignofthecontroller,dynamicinversionisappliedtodealwithstrongcouplingsamongpitchangle,yawangleandrollangle.Therobustnessofsystemisguaranteedbyusingslidingmodevariablestructurecontrolmethod.Inordertorestrainthesaturationofservomechanism,therulesoffuzzygain-schedulingaredesignedbyexpertexperiences.Thesimulationresultsdemonstratethatthemethodisefficientinboththeattitudecontrolofhypersonicvehiclesandthesaturationrestrainofservomechanism.

Hypersonic;Dynamicinversion;Slidingmodecontrol;Fuzzy;Saturationrestrain

2016-05-13

刘海东(1984-)，男，辽宁鞍山人，博士研究生，工程师，主要研究方向为导航、制导与控制；包为民(1960-)，男，浙江镇海人，教授，主要研究方向为导航、制导与控制；李惠峰(1970-)，女，陕西人，教授，主要研究方向为飞行器制导与控制技术。

V448.22+2

A

1006-3242(2017)01-0003-05