经验模型和过程模型对油松林枯损预测的比较1)
2017-08-07廖梓延田相林薛海连王彬孙帅超曹田健陈书军侯琳
廖梓延 田相林 薛海连 王彬 孙帅超 曹田健 陈书军 侯琳
(西北农林科技大学,杨凌,712100)
经验模型和过程模型对油松林枯损预测的比较1)
廖梓延 田相林 薛海连 王彬 孙帅超 曹田健 陈书军 侯琳
(西北农林科技大学,杨凌,712100)
研究采用西北农林科技大学开发的可变密度全林模型QUASSI 1.0,基于赫尔辛基大学开发的CROBAS碳平衡模型框架,融合二类调查数据、文献数据以及解析木数据,进行参数校正及优化,本地化了CROBAS-PT(油松)枯损模块的参数。并根据立地条件和初始密度选取了9个代表性油松林分,以20年为预测期,比较分析了经验模型和过程模型在不同密度、不同地位级条件下对枯损预测的差异,探索有效的林分枯损预测方法。同时采用平均误差、平均绝对误差和平均相对误差分析了过程模型CROBAS-PT与经验模型QUASSI 1.0预测值的偏差。结果表明:对于不同初始密度的油松林,CROBAS-PT和QUASSI 1.0在预测期内均呈现初始密度越大,林分年枯损率越大的规律;对于不同地位级的油松林,无论CROBAS-PT还是QUASSI 1.0在预测期内,林分枯损受立地条件的影响均不敏感。CROBAS-PT枯损预测的机理过程分析说明,油松树冠投影在20~40 a预测期内呈现先增加后降低的趋势。立地质量越好的林分,树冠投影越大,枯损率越大。误差检验分析显示,过程模型CROBAS-PT枯损预测结果符合统计检验要求,尽管CROBAS-PT对于枯损的预测相比经验模型QUASSI 1.0存在一定程度的低估。在缺乏连续观测样地数据,无法保证经验模型的建模数据需求时,采用过程模型方法预测林分枯损不失为一种有效补充。
油松;林木枯损;过程模型;经验模型;秦岭
Chinese pine; Tree mortality; Process-based model; Empirical model; Qinling Mountains
林木的枯损在森林的发育过程中是一件稀有但是非常重要的事件,尽管人们对林木在死亡过程中所发生的内在生理学过程了解甚微,但是树木的枯损却受到林分密度、森林病虫害、林火等因子的影响[1]。林木枯损可以分为自然枯损和非自然枯损,自然枯损主要由于树木间竞争引起,而非自然枯损主要是由于森林容易受到极端气候、病虫害等的干扰导致的林木逐渐死亡[2-4]。林木枯损率模型是林分生长与收获模型体系中的一个重要组成部分,自然枯损预估模型的准确构建对林分生长收获预估,碳汇动态变化等相关研究具有重要意义。
按照生长收获模型分类标准,枯损模型可以分为单木枯损模型和林分枯损模型,同时按建模方法又可分为经验模型、过程模型和混合模型[5]。前人对枯损模型的研究多采用单木和林分水平的经验模型[6]。在单木枯损模型的研究中,通常采用经验方程模拟,比如指数、Weibull、Gamma、负二项、Richards以及Logistic等。Vanclay[7]认为Logistic模型最适合用于分析林木枯损,因此,国内外学者也较多采用Logistic方程来构建单树枯损模型[8-9]。在林分枯损模型的研究中,通常采用差分方程来模拟[10]。上述传统经验枯损模型建模方法变量较少,模型形式简单,然而需要大量的连续观测样地数据才能满足建模需要。
在缺乏有效数据情况下,采用过程模型预测林分枯损是一种有益的尝试[11]。过程模型以光合作用同化CO2为基础,研究和模拟林分生长和收获的全过程及其与环境因子的关系,相比经验模型,其变量复杂,参数众多,模型形式复杂。目前应用较广的过程模型3-PG有48个参数[12]、FOREST-BGC有41个参数[13],CENTURY模型已经发展到5.0版本,参数也随着模型的不断发展逐渐增加[14]。过程模型CROBAS最初是Mäkelä[15]为欧洲赤松(PinussylvestrisL.)而开发的碳平衡模型。该模型共有39个参数,其原理主要基于光截留、光合作用、碳分配等生理过程,现已应用于挪威云杉(Piceaabies)和北美短叶松(PinusbanksianaLamb)等树种[16-17]。
本研究尝试以秦岭油松林为例,采用经过参数本地化的过程模型CROBAS油松版CROBAS-PT,以及西北农林科技大学开发的油松可变密度全林模型QUASSI 1.0[15,18],比较经验模型与过程模型在枯损预测上的差异,探索有效的林分枯损预测方法。
1 研究区概况
油松(Pinustabulaeformis)是秦岭松栎林带主要的针叶树种之一,在秦岭林区主要分布在海拔1 000~1 500 m地带。油松在秦岭坡度较大、土层较薄的山坡、山脊占绝对优势并形成纯林,具有一定的天然更新能力。研究地区为西北农林科技大学火地塘教学林场,该林区地处秦岭南坡中段宁陕县境内,林区地形复杂,山势东高西低,坡度在20°~25°,海拔800~2 474 m。林区年降水量为1 000 mm,雨季集中于7月和8月,年平均温度12.7 ℃,绝对最高温和最低温分别为28.6 ℃和-9.5 ℃,年日照时间为1 327.5 h,生长期约为6个月,属于北亚热带气候类型。土壤主要有山地棕壤、暗棕壤和山地草甸土。
2 研究方法
2.1 数据来源和特征
本研究采用临时样地、解析木和文献多源数据。其中油松临时样地173块,解析木15株。油松临时样地林分特征统计如下(表1)。

表1 油松优势林分特征统计表
2.2 经验模型
本研究所采用的经验模型来源于西北农林科技大学生态仿真优化实验室构建的可变密度全林经验模型QUASSI 1.0版本,具体公式如下:
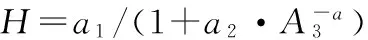
(1)
SDI=N(D/20)β;
(2)
(3)
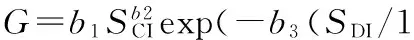
(4)

(5)
N=40 000G/πD2。
(6)


表2 参数估计值
2.3 过程模型
2.3.1 CROBAS模型
CROBAS过程模型基于3种重要关系:(1)树冠表面积与树叶干质量异速相关;(2)树叶和细根干质量之间维持一个功能平衡常数;(3)树叶和树干边材横截面积呈线性相关,也就是著名的Pipe理论[18]。上述3个关系方程为:

(7)
Wr=αrWf;
(8)
Ai=αiWf。
(9)
式中:Wf、Wr分别代表树叶、细根的干质量;Ac表示树冠表面积;Ai为树干边材横截面积;z、ε、αr、αi为参数;i分别表示树干、树枝以及运输根。
模型的核心问题是解决林分平均木的5部分碳储存场所的生物量分配,这5部分分别为:树叶(f)、细根(r)、树干(s)、树枝(b)以及运输根(t),基于上述的理论以及其它假设便可得到树干、树枝和运输根的生物量分别为:
Ws=ρsαs(φsHs+φcHc)Wf;
(10)
Wb=ρbαbφbHcWf;
(11)
Wt=ρtαtφt(Hs+Hc)Wf。
(12)
式中:Ws、Wb、Wt分别代表树干、树枝以及运输根的干质量;Hs为树干高度;Hc为树冠高度;ρs、ρb、ρt分别表示树干、树枝以及运输根的密度;αs、φs、φc、αb、φb、at、φt为参数。通过上列表达式,生物量在树木各个部分的分配就能有效地表达。此外通过光合作用、呼吸作用、自然整枝率以及枯损等部分的模型链接构建整个CROBAS过程模型,模型具体关键公式如下:
G=∑Gi=Y-1(P-R),(i=f,r,s,b,t);
(13)
P=P0(1-e-kl)/N;
(14)
Rm=r1(Wf+Wr)+r2(Ws+Wb+Wt)。
(15)
式中:G为树木总生长量;Gi为分别代表树叶、细根、树干、树枝以及运输根的生长量;P指光合作用生产量;Rm为维持呼吸作用;R指呼吸作用消耗量;Y为转化因子;P0为单位面积最大光合利用率;N为每平方米林木株数;k为消光系数;l为叶面积指数;r1、r2为经验参数。
模型中定义的与竞争有关的林分枯损是从林分中树冠之间开始互相接触而发生的,在CROBAS中C表示树冠投影,指林木之间树冠相互覆盖的面积,其可根据每公顷林分密度(N),以及树冠半径(Hb),具体公式如下:

(16)
dN/dt=-(m0+m1pC)N。
(17)
式中:Cb、m0、m1、p均为参数。
2.3.2 本地化CROBAS-PT参数
基于CROBAS碳平衡模型框架,融合多元数据类型,包括二类调查数据、文献数据、解析木数据等,运用SPSS 22.0软件的规划求解工具,采用生物统计、回归分析(线性回归、多元线性回归和非线性回归)、目标优化等技术对秦岭油松过程模型CROBAS-PT进行参数本地化,具体方法见表4。
CROBAS模型含直接或间接影响自然枯损相关的6个参数:碳有效利用率(Y)、比叶面积(an)、单位面积树冠上的最大光合速率(P0)、消光系数(k)、与自然整枝相关的参数(aq)、与密度无关的枯损参数(m0)等会随着初始林分条件的不同发生一定的范围变化。为此,建立参数优化模型,以林分初始状态为约束条件,在一定范围内校正上述6个参数,极小化油松过程模型CROBAS-PT与经验模型QUASSI 1.0对树高、胸径、蓄积和密度预测值的误差。6个参数优化模型的数学表达式为:

(18)
s.t.x=(x1,x2,…,x6);
(19)
y0=(h0,n0,d0)。
(20)
2.4 林分枯损预测应用
在173个油松临时样地中选取林龄为20a左右,不同密度、不同地位级的9个油松林分(见表3),分别采用QUASSI1.0经验模型以及本地参数化后的CROBAS-PT过程模型进行油松林分枯损动态预测,预测未来20a的油松林分枯损,比较经验模型和过程模型在不同密度、不同地位级下枯损预测的差异。

表3 不同条件下林分初始状态
2.5 误差检验
为检验CROBAS-PT过程模型预测枯损的准确性,本研究运用SPSS 22.0软件对CROBAS-PT与QUASSI 1.0的林分密度、树高、胸径预测值间进行误差统计量分析。将CROBAS-PT、QUASSI 1.0枯损预测结果,经验数据回归得到的林分自然稀疏曲线以及实测临时样地数据进行相关性分析,检验CROBAS-PT枯损预估结果的有效性。检验统计量包括平均绝对偏差(AMRES)、平均误差(MRES)、平均相对误差(AMR),检验公式为:
AMRES=∑|PVcro-PVqua|/n
(21)
MRES=∑(PVcro-PVqua)/n
(22)
AMR=(∑(PVcro-PVqua)/∑PVcro)×100%。
(23)
PVcro表示CROBAS-PT预测结果,PVqua表示QUASSI 1.0预测结果,PV为状态变量(树高H,胸径D,蓄积量V,密度N)。平均误差、平均相对误差越小,说明CROBAS-PT状态变量预测值与QUASSI 1.0状态变量预测值越接近,模型的检验符合精度要求。误差绝对值越小,模型精度越高。
3 结果与分析
3.1 油松过程模型CROBAS-PT参数本地化
进行参数优化后得到的参数x1~x6的值,随着林分初始状态(密度、地位级等)不同,会呈现出小范围的变化,优化后的目标值(极小化误差值)集中于0.13~0.27。9个林分的枯损参数优化结果见表5。

表4 CROBAS-PT(油松)本地化参数值
注:表中x=(x1,x2,…,x6)为待优化向量。

表5 参数优化结果
注:PT表示CROBAS-PT,数字代表林分编号。
3.2 过程模型和经验模型树高、胸径预测对比
从图1可以看出,过程模型CROBAS-PT与经验模型QUASSI 1.0对不同初始密度的油松林树高和胸径预估值的误差都非常接近,而对于不同立地条件油松林,树高和胸径预估值的误差则随着地位级增加而增大。
3.3 林分枯损对初始密度的敏感性
从图2可以看出,在不同初始密度下,枯损率明显不同,总体呈现出初始密度高的林分年枯损率大于初始密度低的林分。无论是CROBAS-PT还是QUASSI 1.0在模拟林分枯损时,林分密度都随着林龄的增加而降低,且均呈现出斜率(枯损率)逐渐降低的趋势。在整个模拟过程中,CROBAS-PT预测的林分密度前期高于QUASSI 1.0预测值。然而,36 a以后初始密度较低林分(1 000株/hm2)的预测值逐渐低于后者,初始密度较高林分(1 500~2 000株/hm2)的拐点则出现在38 a以后。

图1 过程模型与经验模型对不同初始密度和地位级树高、胸径预估对比

图2 过程模型与经验模型对不同初始密度枯损预估对比
3.4 林分枯损对立地条件的敏感性
图3可以看出,CROBAS-PT以及QUASSI 1.0在20 a模拟周期内,林分密度变化受到立地条件的影响很小,地位级I、II、III的相关系数高达0.99,经验模型和过程模型对林分枯损预测在不同地位级间均无显著性差异。

图3 过程模型与经验模型枯损预估对比
从图4可以看出,在20~40 a内,I地位级树冠投影高于II地位级树冠投影,III地位级树冠投影明显低于I、II。I地位级,20~30 a,油松树冠投影随着年龄增加而呈现出斜率逐渐降低的增长趋势;30 a时,树冠投影达到最大约为1.10;30 a以后,随着年龄增加而呈现出斜率逐渐增加的下降趋势;II地位级,20~31 a,油松树冠投影随着年龄增加而呈现出斜率逐渐降低的增长趋势;31 a时,树冠投影达到最大约为1.07;33 a以后,随着年龄增加而呈现出斜率逐渐增加的下降趋势。III地位级,20~32 a,油松树冠投影随着年龄增加而呈现出斜率逐渐降低的增长趋势;32 a时,树冠投影达到最大约为0.99;32 a以后,随着年龄增加而呈现出斜率逐渐增加的下降趋势。
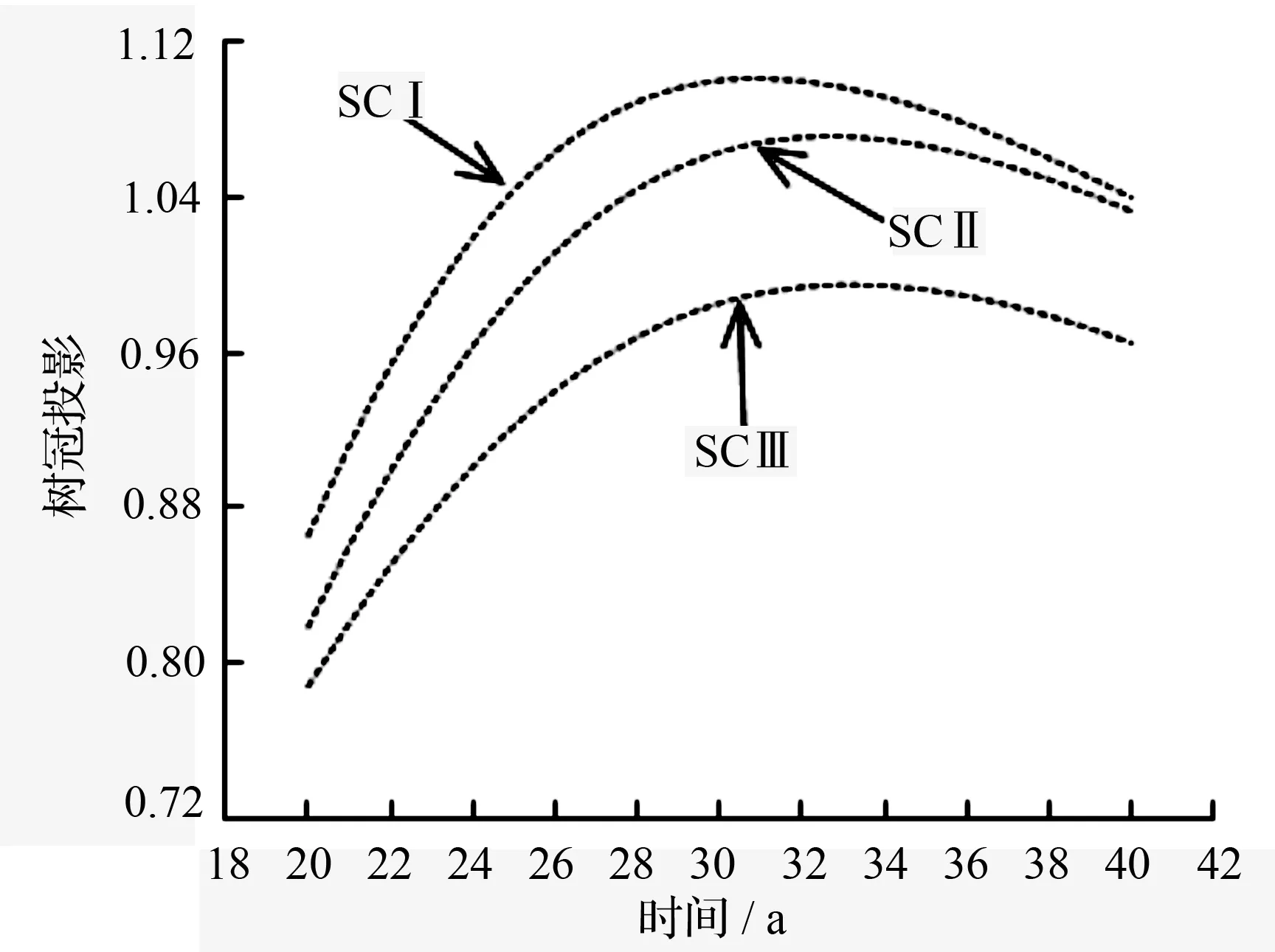
图4 不同地位级树冠投影模拟
3.5 误差检验
3.5.1 实测数据检验
图5展示了自然稀疏曲线、QUASSI 1.0与CROBAS-PT以及实测临时样地的胸径与林分密度的关系。CROBAS-PT与QUASSI 1.0模型预测值在林分初始密度为2 000、1 500、1 000株/hm2时,相关系数分别为0.982、0.981、0.978。从图5可以看出,传统生物统计学得出的自然稀疏曲线,代表了油松林实测林分密度自然稀疏的普遍情况。而CROBAS-PT
以及QUASSI 1.0在不同初始林分状态预测林分枯损时,其最终(胸径20 cm以后)都会接近于自然稀疏曲线,并且CROBAS-PT的这种趋势表现更为明显。
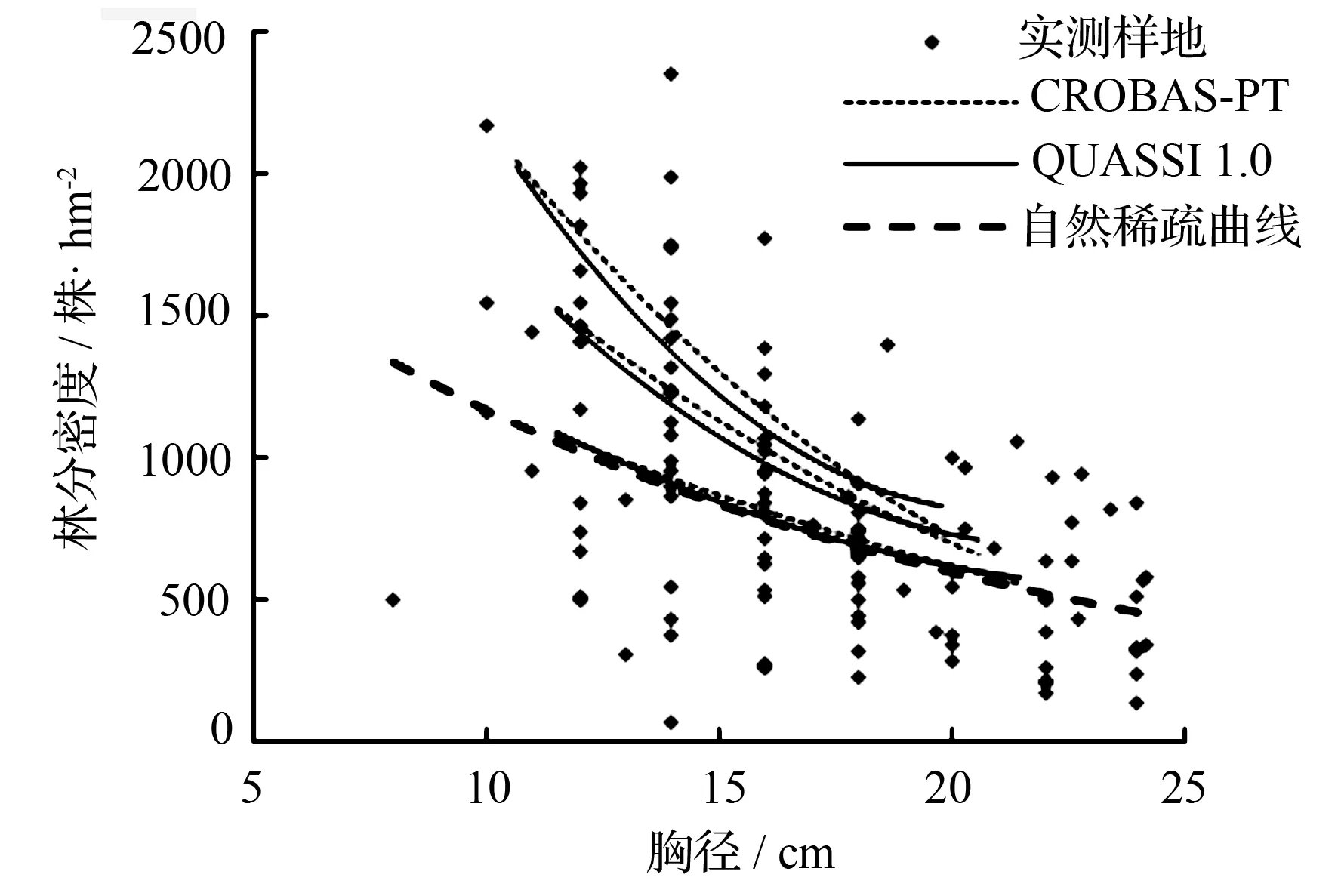
图5 实测自然稀疏与过程模型,经验模型预测结果对比
3.5.2 统计量检验
从表6可以看出,针对不同林分类型,CROBAS-PT林分密度的预测结果间平均绝对偏差(AMRES)、平均误差(MRES)均在92株/hm2以下,平均相对误差(MRES)均小于0.085%。此外树高预测的结果间平均绝对偏差、平均误差均在0.269以下;平均相对误差均小于0.028%。胸径的预测结果间平均绝对偏差、平均误差均在0.318;平均相对误差均小于0.018%。各检验指标显示CROBAS-PT树高预测结果与QUASSI 1.0树高预测偏差低于0.27 m,胸径预测偏差低于0.32 cm,模型检验符合精度要求。

表6 各预测变量检验结果
注:表中N1000、N1500、N2000分别表示林分初始密度为1 000、1 500、2 000株·hm-2。
检验结果表明,在不同地位级下,树高、胸径误差由大到小的顺序为:SC III、SC II、SC I,密度误差与树高胸径相反,密度误差由大到小的顺序为:SC I、SC II、SC III;在不同初始密度下,树高误差由大到小的顺序为:1 000、1 500、2 000株·hm-2,胸径误差与密度并未呈现明显关系,而密度误差由大到小的顺序为:2 000、1 500、1 000株·hm-2。
4 结论与讨论
CROBAS-PT过程模型与QUASSI 1.0经验模型相比较,对于枯损的预测存在一定的低估。研究结果表明,初始林分密度越大的林分,其林分结构越不稳定,林木之间竞争也越大,导致林木年枯损率也越大,而地位级越高的林分,立地条件越好,树冠生长越好,树冠越快达到郁闭,树冠投影越大,年枯损率越大。
4.1 不同建模方法对预测结果的影响
CROBAS-PT过程模型对于枯损的预测相比较QUASSI 1.0经验模型存在一定的低估。Mäkelä et al[27]认为当林分为严格意义上的同龄林时,会导致所有的树木生长发育缓慢,同时很少有受压迫死亡的树木产生,此外,如果林分为异龄林,林分内大树有利用更多生长资源的能力,小树木将很快受到荫蔽,竞争比纯林更加激烈,会加速异龄林内小树的枯损概率,导致最终林分密度比同龄林低。研究发现采用过程模型比经验模型在预估林分枯损上,会低估林分年枯损率,这也与QUASSI 1.0经验模型建模数据是基于实际调查样地的数据,秦岭油松林分很少为绝对同龄,一般采用平均木年龄代替林分平均年龄;而CROBAS-PT过程模型在预测林分枯损的时候,是将林分内所有树木模拟成生长一致的同龄林,因此,其模拟的林分竞争相比较经验模型较低,枯损也会有所低估。但在CROBAS模型系统误差允许的情况下,CROBAS-PT与QUASSI 1.0枯损的预测值相对误差仍然可以控制在0.085%以内,说明本地化参数后的CROBAS-PT过程模型能有效的适用于秦岭油松枯损预测。
4.2 CROBAS-PT预测枯损的有效性与局限性
不同地位级油松生长速率不同,但是其林分密度随时间的变化相差不大,这也印证了Yoda et al[28]指出的自然稀疏斜率,也就是枯损率几乎不受林龄和立地质量影响的观点。此外CROBAS-PT以及QUASSI 1.0在不同初始林分状态,预测林分枯损时,最终都会十分接近于自然稀疏曲线,并且对于初始林分密度为1 000株/hm2的林分,,两者的预测曲线与自然稀疏曲线几乎重叠,这种规律也印证了CROBAS-PT预测枯损的有效性。
本研究基于CROBAS碳平衡模型框架,对CROBAS-PT秦岭油松过程模型进行参数本地化及参数校正和优化,在满足树高、胸径准确预估的前提下,其枯损预测结果符合统计检验的要求,能满足林分枯损动态预估应用的需要。然而,仍难以预测生态干扰的多变性,如气候压力、火灾等一些破坏性事件[29]。因此,提出的与密度、立地质量有关的枯损预测也仅仅适用于自然枯损。
传统经验枯损模型的研究有一个共同特点,就是依赖大量的连续复位监测样地数据,在缺乏连续观测样地数据情况下,采用CROBAS碳平衡过程模型预测林分枯损,为缺少数据情况下建模提供了一种新的思路。相比较传统的采用生物统计学构建的林分枯损模型而言,CROBAS-PT继承了过程模型的优势,既包含了经验模型的特征又具有机理模型的功能,同时能够从过程机理上去解释林分枯损的原因。例如,CROBAS枯损模块的理论依据是郁闭度的增大导致竞争加剧(主要是对光照的竞争),引起一部分树木产生枯损,树冠死亡,树冠投影降低。由于林木枯损,剩下的树木的生长潜力较低,不能在短时间内填补树冠遮蔽面积,最终树冠投影达到一个动态平衡[15]
传统经验模型参数往往是固定的[2],本地化参数后的CROBAS-PT过程模型的枯损模块参数具有一定可变动范围,能根据不同初始林分条件合理的在一定范围内选择合适的参数进行枯损动态预测,增加了模型应用的普适性。但需要通过增加更多的实测数据进行本地参数化和验证,以更准确地模拟林分枯损。CROBAS-PT在枯损模块参数本地化时采用规划求解进行参数优化,优化结果能否收敛依赖于初始赋值。如果优化更为复杂的过程模型参数时,需要采用高级的人工智能算法(差分演化算法)来优化参数[30],从优化算法上改进和提高参数优化的准确性。
[1] MONSERUD R A, STERBA H. Modeling individual tree mortality for Austrian forest species[J]. Forest Ecology and Management,1999,113(2/3):109-123.
[2] VANCLAY J K. Modelling forest growth and yield: applications to mixed tropical forests[M]. Wallingford, UK: CAB International,1994.
[3] PEET R K, CHRISTENSEN N L. Competition and tree death[J]. Bioscience,1987,37(8):586-595.
[4] KNEESHAW D D, BERGERON Y. Canopy gap characteristics and tree replacement in the southeastern boreal forest[J]. Ecology,1998,79(3):783-794.
[5] AVERY T E, BURKHART H E. Forest measurements[M]. New York: McGraw-Hill,2001.
[6] 张雄清,雷渊才,段爱国,等.林分动态变化模型研究进展[J].世界林业研究,2013,26(3):63-69.
[7] VANCLAY J K. Growth models for tropical forests: a synthesis of models and methods[J]. Forest Science,1995,41(1):7-42.
[8] CAO Q V. Prediction of annual diameter growth and survival for individual trees from periodic measurements[J]. Forest Science,2000,46(1):127-131.
[9] 向玮,雷相东,刘刚,等.近天然落叶松云冷杉林单木枯损模型研究[J].北京林业大学学报,2008,30(6):90-98.
[10] CLUTTER J L, FORTSON J C, PIENAAR L V, et al. Timber management, a quantative approach[M]. New York: Wiley,1983.
[11] WEISKITTEL A R, HANN D W, KERSHAW J A, et al. Forest growth and yield modeling[M]. New York: Wiley,2011.
[12] COOPS N C, WARING R H. Estimating forest productivity in the eastern siskiyou mountains of southwestern oregon using a satellite driven process model 3-PGS[J]. Canadian Journal of Forest Research,2001,31(1):143-154.
[13] RUNNING S W, GOWER S T. FOREST-BGC, A general model of forest ecosystem processes for regional applications: ii. dynamic carbon allocation and nitrogen budgets[J]. Tree Physiology,1991,9(1/2):147-160.
[14] 方东明,周广胜,蒋延玲,等.基于CENTURY模型模拟火烧对大兴安岭兴安落叶松林碳动态的影响[J].应用生态学报,2012,23(9):2411-2421.
[15] Mäkelä A. A carbon balance model of growth and self-pruning in trees based on structural relationships[J]. Forest Science,1997,43(1):7-24.
[16] KANTOLA A, MKELA. Crown development in Norway spruce [Piceaabies(L.) Karst.][J]. Trees,2004,18(4):408-421.
[17] SCHNEIDER R S, BERNINGER F B, UNG C H, et al. Calibrating jack pine allometric relationships with simultaneous regressions[J]. Canadian Journal of Forest Research,2008,38(10):2566-2578.
[18] SHINOZAKI K, YODA K, HOZUMI K, et al. A quantitative analysis of plant form: The pipe model theory. II. Further evidence of the theory and its application in forest ecology[J]. Japanese Journal of Ecology,1964,14(4):133-139.
[19] 徐有明.油松木材基本密度的变异[J].华中农业大学学报,1991,10(3):281-285.
[20] 陈存根,彭鸿.秦岭火地塘林区主要森林类型的现存量和生产力[J].西北林学院学报,1996,11(S1):92-102.
[21] 张晶.油松、侧柏、白皮松根系径级结构及其与呼吸特性关系的研究[D].北京:北京林业大学,2006.
[22] VANNINEN P, MKELA. Fine root biomass of scots pine stands differing in age and soil fertility in southern Finland[J]. Tree Physiology,1999,19(12):823-830.
[23] YODER B J, RYAN M G, WARING R H, et al. Evidence of reduced photosynthetic rates in old trees[J]. Forest Science,1994,40(3):513-527.
[24] 侯琳,雷瑞德,王得祥,等.秦岭火地塘林区油松群落乔木层的碳密度[J].东北林业大学学报,2009,37(1):23-25.
[25] 邱瑞,侯琳,袁杰,等.秦岭火地塘林区油松生长季土壤呼吸研究[J].西北农林科技大学学报(自然科学版),2011,39(10):87-93.
[26] 宋子炜,郭小平,赵廷宁,等.北京山区油松林光辐射特征及冠层结构参数[J].浙江林学院学报,2009,26(1):38-43.
[28] YODA K, KIRA T, OGAWA H, et al. Self-thinning in overcrowded pure stands under cultivated and natural conditions[J]. Journal of Biology,1963,14:107-129.
[29] STAGE A R. Prognosis model for stand development[R]//Research Paper INT-137, USDA Forest Service,1973.
[30] STORN R, PRICE K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization,1997,11(4):341-359.
1)国家自然科学基金面上项目(31170586);国家自然科学基金面上项目(31670646);全国森林经营基础研究项目(1692016-07)。
廖梓延,男,1991年8月生,西北农林科技大学生态仿真优化实验室,硕士研究生。E-mail:289486136@qq.com。
曹田健,西北农林科技大学生态仿真优化实验室,教授。E-mail:Cao@nwsuaf.edu.cn。
2016年11月10日。
S757.1
责任编辑:王广建。
Comparison of Empirical and Process-based Methods on Mortality Predictions forPinustabulaeformisStands//Liao Ziyan, Tian Xianglin, Xue Hailian, Wang Bin, Sun Shuaichao, Cao Tianjian, Chen Shujun, Hou Lin(Northwest A&F University, Yangling 712100, P. R. China)//Journal of Northeast Forestry University,2017,45(3):51-57,62.
Based on carbon balance framework of CROBAS developed by University of Helsinki and variable density empirical model QUASSI 1.0 developed by Northwest Agriculture and Forestry University, and multi-source inventory data, the parameters of CROBAS-PT (Pinustabulaeformis) were calibrated. The effects of stand site and density on mortality predictions were analyzed, based on a 20-year simulation of 9 plots to compare the empirical model and process based model on mortality predictions. Mean error, mean absolute error and mean relative error were calculated to compare the results from CROBAS-PT and QUASSI 1.0. The mortality predictions are sensitive to different initial density, but insensitive to site. The stands of good site perform high crown projection area and mortality. Although the CROBAS-PT model predicts lower level of mortality than QUASSI 1.0 model, the process-based CROBAS-PT model can be used for mortality predictions, as its results match the statistical test. Since processed model explains the theory of forest mortality, it can be an effective method to predict the mortality ofP.tabulaeformisin the region where the data are lacking.
