基于混合效应模型的大兴安岭地被可燃物含水率模型1)

邢俊景 曲智林

(东北林业大学，哈尔滨，150040)



基于混合效应模型的大兴安岭地被可燃物含水率模型1)

邢俊景 曲智林

(东北林业大学，哈尔滨，150040)

基于黑龙江省大兴安岭林区南瓮河生态站的落叶松(Larixgmelinii)林、蒙古栎(Quercusmongolica)林、落叶松白桦(Betulaplatyphylla)混交林3种典型林分的288组可燃物含水率数据，选择基于平衡含水率的可燃物含水率实时变化模型为基础模型，采用非线性混合效应(NLME)模型方法，以林分因子作为随机效应，建立具有混合效应的可燃物含水率的实时变化预测模型，并通过给残差方差增加权重的方法解决异方差性问题。结果表明:考虑随机效应和异方差结构的可燃物含水率实时变化NLME预测模型的拟合效果(MAE=0.716 7，MRE=0.026 6)优于不含随机效应的可燃物含水率实时变化预测模型(MAE=0.815 6，MRE=0.031 2)；其中以常数加幂函数作为异方差结构的模型精度最高(AIC=547.72，BIC=581.29，-2LL=527.72)且明显优于未给残差方差增加权重的可燃物含水率实时变化NLME预测模型(AIC=961.65，BIC=988.50，-2LL=945.65)。利用独立样本数据对模型进行检验，检验结果表明，对于可燃物含水率实时变化的预测，考虑随机效应和异方差结构的NLME模型的检验精度(MAE=0.495 8，MRE=0.034 2)比利用最小二乘法拟合的多元非线性回归模型(MAE=0.588 5，MRE=0.588 5)有所提高,说明基于混合效应模型的可燃物含水率实时变化模型可以很好地描述区域尺度上不同林分类型的可燃物含水率实时变化规律。

大兴安岭；可燃物含水率；非线性混合效应模型；异方差

Daxing’an Mountains; Fuel moisture content; Nonlinear mixed effects models (NLMEMs); Heteroscedasticity

森林可燃物是林火发生的物质基础和首要条件[1]，其含水率多少是决定森林火灾发生的重要指标之一,研究森林可燃物含水率变化的规律,有利于人类了解森林火灾发生的规律。目前，可燃物含水率预测模型的方法主要包括4种：基于平衡含水率的方法、气象要素回归法、遥感估测法、基于过程模型的方法。在这4种方法中，基于平衡含水率的预测方法应用最广，在美国、加拿大等国家的森林火险等级系统中已广泛应用，且预测效果较好[2]。近年来，许多学者针对不同林分类型对可燃物含水率变化进行研究。金森等[3-4]针对江西、云南典型林分建立可燃物含水率预测模型。杨博文等[5]分析了帽儿山两林分气温与地表可燃物温度差异及对可燃物含水率预测的影响。周振超等[6]对哈尔滨城市林业示范基地典型林分地表死可燃物含水率与气象因子的关系进行了研究。胡海清等[7]预测了大兴安岭典型林分地表死可燃物含水率动态变化。上述研究都是在林分尺度上对可燃物含水率进行研究，林分类型的不同决定了可燃物含水率变化规律不同，为了便于分析不同林分类型对地被可燃物含水率变化的影响，建立含有林分因子的可燃物含水率模型是非常重要的。

混合效应模型是指模型中部分参数或全部参数由固定效应和随机参数的混合组成,该模型为分析分组数据提供了灵活和强有力的工具。因此，利用混合效应模型来分析不同林分因子的森林可燃物含水率变化规律是可行的。

基于黑龙江省大兴安岭林区南瓮河生态站采集的落叶松林、蒙古栎林、落叶松白桦混交林3种典型林分的地被可燃物含水率和相应的气象因子数据，采用非线性混合效应(NLME)模型的方法，考虑林分因子的随机效应和数据间的异方差性，建立可燃物含水率实时变化模型，并利用独立样本数据对模型的精度进行检验，以期建立具有混合效应的可燃物含水率预测模型，进而使区域尺度上不同林分类型的可燃物含水率模型具有相容性，为区域尺度上的林火预测提供理论依据。

1 研究区概况

研究区位于黑龙江省大兴安岭南瓮河生态站(125°7′55″～125°50′5″E，51°5′7″～51°39′24″N)。该区为大兴安岭支脉，伊勒呼里山南坡，属低山丘陵地貌，地形起伏不大，地势为北高南低，西高东低，海拔高一般为500～800 m。气候属寒温带大陆性季风气候，冬季受西伯利亚寒流的影响，异常寒冷，冬季漫长，长达9个月，年平均气温-3 ℃，极端最低温度-48 ℃。相反，温暖季节甚短，夏季最长不超过1个月，极端最高气温36 ℃。年降水量500 mm左右，80%以上皆集中于温暖季节(7—8月)。而5—6月常有明显旱象，形成云雾少，日照强，温度低的气候特点，致使林木草原火险增多。主要林分为落叶松(Larixgmelinii)、山杨(Populusdavidiana)、白桦(Betulaplatyphylla)、蒙古栎(Quercusmongolica)、落叶松白桦混交林、山杨白桦混交林等。

2 研究方法

2.1 数据来源

在南瓮河生态站分别在落叶松林、蒙古栎林、落叶松白桦混交林内设置样地。在样地内设置数据收集点，观测仪器每小时自动收录地被可燃物含水率，以及生态站实时观测气象数据，主要包括气温、空气相对湿度、风速、降雨量等。本文所使用的数据为2015年6月11日00时—2015年6月14日23时的观测数据，其中2015年6月11日00时—2015年6月13日23时的观测数据数据作为建模数据，2015年6月14日00时—2015年6月14日23时的观测数据作为检验数据，用于模型检验，统计信息见表1。数据处理利用R和SPSS 18.0软件完成。

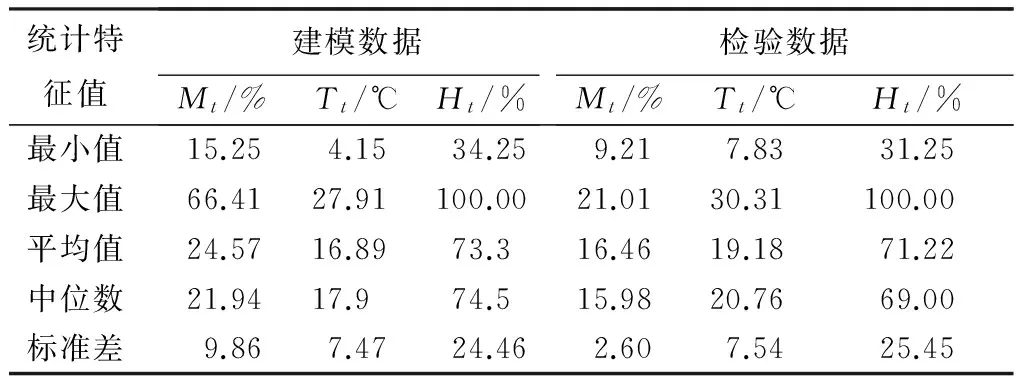
表1 建模数据和检验数据统计信息

注：Mt、Tt、Ht分别表示t时刻的可燃物含水率、气温和空气相对湿度。

2.2 混合效应模型

降水对可燃物含水率的变化有明显的影响，而降水量与可燃物含水率之间的关系比较复杂，本文建立的模型和使用的方法均基于无降水的情况。

由于可燃物含水率的瞬时变化率主要受可燃物的含水率与其平衡含水率的影响[8]。因此可燃物含水率变化模型为：

dMt/dt=k(Et-Mt)。

(1)

式中：Mt为可燃物t时刻的含水率；Et为可燃物t时刻的平衡含水率。

将方程(1)离散化，可得到可燃物含水率实时变化预测模型(1 h内变化)：

Mt+1=(1-k)Mt+k·g(Tt，Ht)。

(2)

式中：Tt为t时刻的温度；Ht为t时刻的空气相对湿度；Et=g(Tt，Ht)为环境因子对平衡含水率的响应函数。

Lindstrom et al[9]定义NLME模型为：

yij=f(φij，vij)+εij，i=1、…、N，j=1、…、n。

(3)

式中：yij=Mij+1为第i个林分j+1时刻的可燃物含水率；yij为第i个林分j+1时刻的可燃物含水率所对应的影响因子，包括第i个林分j时刻的可燃物含水率(Mij)、气温(Tij)和空气相对湿度(Hij)；N为林分因子的个数，取值为3；ni为第i个林分可燃物含水率数据的组数，取值为72；εij为第i个林分j时刻观测数据的误差项值；φij是出现在非线性函数f中，由固定效应和随机效应组成的形式参数向量，非线性函数f的表达式：

f=(1-k)Mij+k·g(Tij，Hij)。

(4)

2.3 形式参数构造与误差结构

根据Pinheiro et al[10]在基础模型中选择不同的固定效应参数组合添加随机效应组成混合参数进行模拟，选择模型收敛及模拟精度最高的混合效应模型作为该水平的最优模型，即采用赤池信息量准则(AIC)、贝叶斯信息准则(BIC)、负二倍的对数似然值(-2LL)等模型的评价指标，对模型的精度进行比较分析，这3个模型的评价指标值越小，其模拟精度越高。

为避免模型参数过多，本文利用似然比检验[11]：

LRT=2lg(L1/L2)=2(lgL1-lgL2)。

(5)

其中：L1为复杂模型的最大似然函数值；L2为简单模型的最大似然函数值，LRT近似服从λ分布，且其自由度为k1-k2。给定显著性水平α=0.05，当LRT≥λα(k1-k2)拒绝原假设，说明复杂模型与简单模型差异显著，选择随机效应参数较多的复杂模型；反之，接受原假设选择随机效应参数较少的简单模型。

协方差矩阵R反映了数据间的异方差性，本研究试图通过给残差方差增加权重的方法消除数据间的异方差性。从自变量为当前时刻的含水率的指数函数、幂函数和常数加幂函数3个候选模型中由AIC、BIC、-2LL和似然比检验确定一个效果最好的残差方差模型[12]。其结构表达式为：

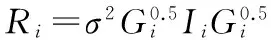
(6)

Var(εij)=σ2exp(2δMij)；

(7)

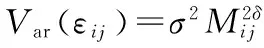
(8)

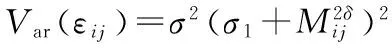
(9)

其中：σ2为剩余方差；Ri为i林分样地数据的协方差矩阵；为Gi为ni×ni维的对角矩阵，反映混合效应模型的随机效应异方差性；Ii为ni×ni维的方差矩阵，描述了随机效应的自相关性，假定Ii为ni×ni维的单位矩阵；Mij为第i林分样地内第j时刻的可燃物含水率；δ、δ1、δ2为待估参数。

2.4 模型误差分析

本研究利用含水率平均绝对误差(MAE)、含水率平均相对误差(MRE)这两个指标对非线性多元回归模型和NLME模型进行精度评价，MAE和MRE的值越接近0，说明模型的精度越高[13]。

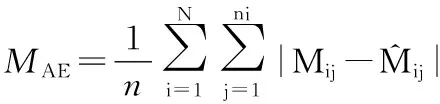
(10)

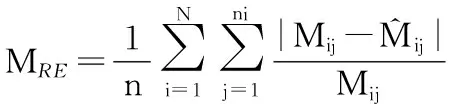
(11)

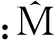
3 结果与分析

3.1 基础模型的确定

选择四种不同的环境影响因子对可燃物平衡含水率的响应方程，采用最小二乘法拟合可燃物含水率实时变化模型，结果见表2。

表2 基于不同平衡含水率方程的可燃物含水率模型拟合结果比较

注：*表示一般显著；** 表示显著；*** 表示非常显著。

从表2中可以看出模型Ⅰ的平均绝对误差(MAE)和平均相对误差(MRE)最小，从评价指标的大小方面考虑应该选择模型Ⅰ为基础模型。但是从系数的显著性来看，模型Ⅰ的参数c的显著水平大于0.1，显著性不强，因此，选择每一个参数显著性水平都小于0.02，且平均绝对误差(MAE)和平均相对误差(MRE)相对最小的模型Ⅳ作为基础模型：

Mij+1=(1-k)Mij+k(a+bHij+cTijHij)。

(12)

3.2 随机效应参数的确定

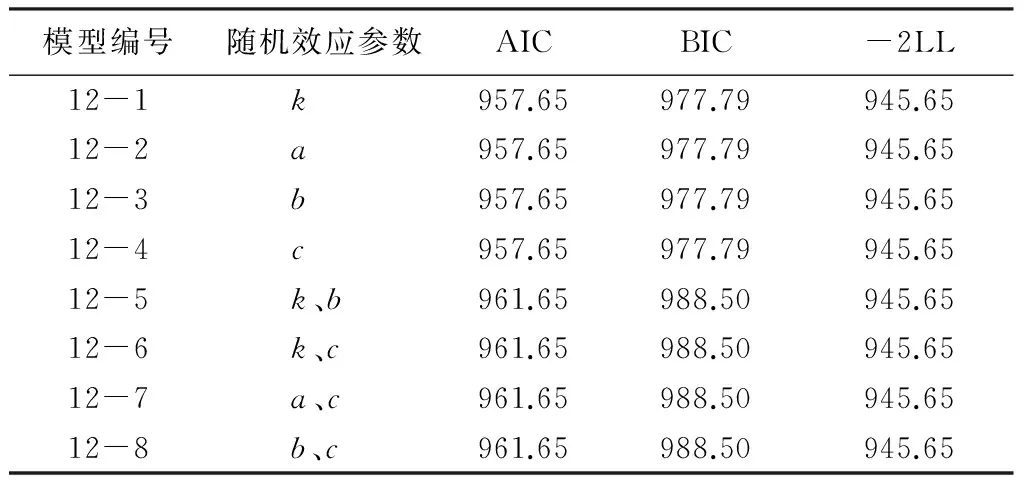
以林分因子作为随机效应，考虑不同随机效应参数的组合，利用R语言的nlme功能，基于模型12建立NLME模型，并对模型的拟合精度进行比较。不同随机效应参数组合的模型拟合精度见表3。

对于可燃物含水率模型，只有8种NLME模型收敛，其中模型12-1、12-2、12-3、12-4的AIC、BIC值完全相等，模型12-5、12-6、12-7、12-8的AIC、BIC值完全相等，并且各个模型差别不大。参数k代表水分的扩散系数，参数a、b、c与平衡含水率相关，从实际意义考虑林分因子对这4个参数均有影响，可以添加随机效应，本文选择以k和b同时作为混合参数的模型(12-5)建立可燃物含水率的NLME模型：

Mij+1=(1-(k+uik))Mij+(k+uik)(a+(b+uib)Hij+cTijHij)。

(13)

式中：uik为模型中参数k考虑林分因子的随机效应参数，uib为模型中参数b考虑林分因子的随机效应参数。

表3 基于不同随机效应参数组合的可燃物含水率模型拟合精度比较

模型编号随机效应参数AICBIC-2LL12-1k957.65977.79945.6512-2a957.65977.79945.6512-3b957.65977.79945.6512-4c957.65977.79945.6512-5k、b961.65988.50945.6512-6k、c961.65988.50945.6512-7a、c961.65988.50945.6512-8b、c961.65988.50945.65

3.3 异方差结构的NLME模型

借助模型的拟合值-残差分布图可以直观地判断出数据间是否存在异方差性[14]，图1a、图1b分别是传统非线性多元回归模型与考虑随机效应和异方差结构的混合效应模型的可燃物含水率拟合值-残差分布结果。从图1a可以看出，采用最小二乘法拟合的可燃物含水率的残差是随着拟合值的增大而增大的，表明数据间存在异方差。为解决异方差问题，用幂函数、指数函数和常数加幂函数作为异方差结构对模型13进行改进，结果见表4。从表4中可知，AIC、BIC、-2LL等评价指标均明显降低，说明考虑异方差结构的NLME模型明显提高了模型的预估能力，且与不考虑异方差结构的NLME模型相比具有显著差异，其中以常数加幂函数作为异方差结构的NLME模型(模型13-3)效果最好。利用建模数据对模型13-3进行拟合，最终得到可燃物含水率的NLME模型：

Mij+1=(1-(0.071+uik))Mij+(0.071+uik)(13.866+(0.182+uib)Hij-0.007TijHij)。

(14)

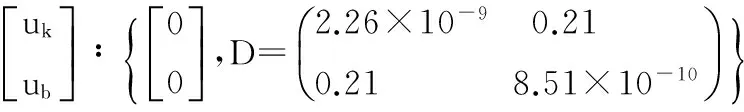
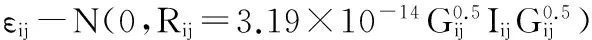
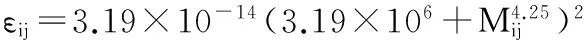
图1b为模型14的拟合值-残差分布图，可以看出该模型能够在一定程度上消除数据间的异方差。

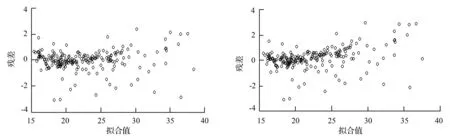
a.传统最小二乘法模拟的残差分布 b.混合效应模拟的残差分布

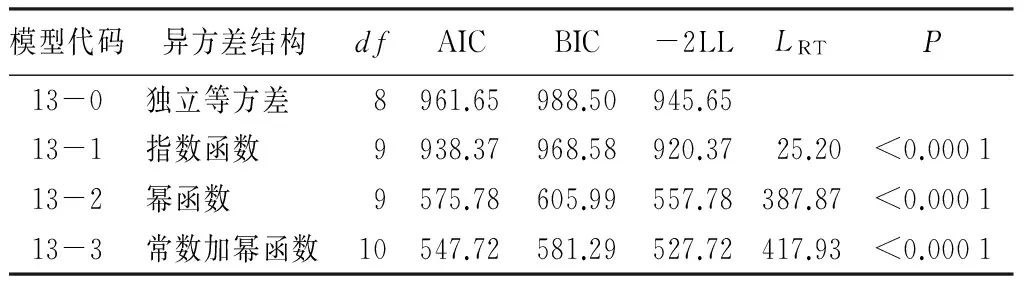
图1 传统非线性多元回归模型和混合效应模型模拟结果残差分布

3.4 模型检验

基于建模数据和检验数据分别计算模型12和模型14的MAE和MRE指标(见表5)。从表5可知，可燃物含水率的NLME模型(模型14)的拟合精度和检验精度均优于基础模型(模型12)。

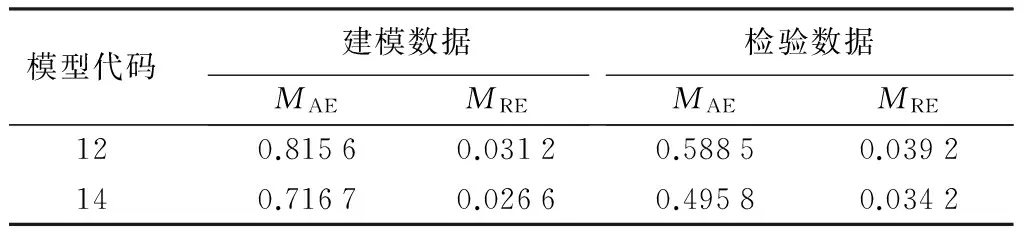
表5 基础模型与混合效应模型模拟结果比较

3.5 不同林分可燃物含水率的差异性

与一般的非线性回归模型不同，混合效应模型考虑了不同林分类型可燃物含水率变化的差异，把误差分解成两部分，一部分为因林分因子不同而产生的随机效应，另一部分是随机误差。由于混合效应模型中各参数具有明确的生物学意义，因此，根据各自随机效应取值大小可反映出相应的随机效应因子对可燃物含水率大小的影响程度[14]。由于模型参数中，固定效应参数恒取一个值，在相同气象条件下(即温度与相对湿度相同)对于同一个初始可燃物含水率，随机效应参数uik越小，可燃物含水率的变化越小；而随机效应参数uib越大，平衡含水率越大，可燃物含水率的变化越大。

表6 不同林分的随机作用参数

表6是不同林分随机作用参数值，由于这些随机效应是由林分因子的差异产生的，因此它们的值可以反映在相同的气象条件下当初始可燃物含水率相同时，经过1小时后不同林分可燃物含水率的差异性。不同林分对水分扩散因子的影响程度由大到小的顺序为：落叶松林、落叶松白桦混交林、蒙古栎林；不同林分对平衡含水率的影响程度由大到小的顺序为：蒙古栎林、落叶松白桦混交林、落叶松林。

4 结论

1)利用单水平NLME模型方法，基于多元非线性回归模型建立了大兴安岭典型林分地表可燃物含水率实时变化预测模型，并考虑了不同随机效应参数的组合，用AIC、BIC、和-2LL及LRT对模型的拟合精度进行检验。结果表明：选择以k和b同时作为混合参数建立的单水平NLME模型，从实际生物意义角度考虑是合理的，充分反映出林分因子的影响。

2)在模型建立过程中，通过残差方差增加权重的方法，解决数据间的异方差问题，与传统的多元线性回归模型相比，考虑随机效应和异方差结构的混合效应模型，可以很好地反映总体的可燃物含水率变化趋势，还可以反映不同林分对可燃物含水率变化的差异，同时消除数据间的异方差性，进而提高模型的预估精度。

3)选择大兴安岭林区3个典型林分的地被可燃物含水率的数据来建立的NLME模型，分析表明林分类型的不同对可燃物含水率变化的影响是不同的。由于数据的原因，对于大兴安岭林区其他林分类型本文没有进行研究，因此，本文建立的混合效应模型只适用于文中提到的3种典型林分。

4)具有混合效应的可燃物含水率模型，是反映林分尺度上的可燃物含水率实时变化规律，如果去掉混合效应，则可以描述区域尺度上的可燃物含水率实时变化规律。如果具有混合效应的模型与各林分分别建模差别较小，并且各林分单独建模的数据较少时，也可通过建立具有混合效应模型来实现。

[1] 田甜，邸雪颖．森林地表可燃物含水率变化机理及影响因子研究概述[J]．森林工程，2013，29(2):21-25.

[2] MATTHEWS S， MCCAW W L， NEAL J E， et al． Testing a process-based fine fuel moisture model in two forest types[J]. Canadian Journal of Forest Research，2006，37(1):23-35.

[3] 金森，刘万龙.江西南昌典型林分地表死可燃物含水率预测：方法优选与适用性分析[J].中南林业科技大学学报，2014，34(11)：1-8.

[4] 金森，刘周勇.昆明典型地表死可燃物含水率预测模型的研究[J].中南林业科技大学学报，2014，34(12)：7-15.

[5] 杨博文，陈鹏宇，金森.帽儿山两林分气温与地表可燃物温度差异及对可燃物含水率预测的影响[J].林业科学，2015，51(7)：91-98.

[6] 周振超，刘安婧，赵磊森，等.典型林分地表死可燃物含水率与气象因子的关系：以哈尔滨城市林业示范基地典型可燃物为例[J].林业科技情报，2016，48(2)：4-11.

[7] 胡海清，陆昕，孙龙，等.大兴安岭典型林分地表死可燃物含水率动态变化及预测模型[J].应用生态学报，2016，27(7)：2212-2224.

[8] NELSON R M. Prediction of diurnal change in 10hour fuel stick moisture content[J]. Canadian Journal of Forest Research，2000，30(7):1071-1087.

[9] LINDSTROM M J， BATES D M． Nonlinear mixed effects models for repeated measures data[J]． Biometrics，1990,46(3):673-687.

[10] PINHEIRO J C， BATES D M． Mixed effects models in SandS-Plus[M]． New York: Spring-Verlag，2000.

[11] FANG Z， BAILEY R L． Nonlinear mixed effects modeling for slash pine dominant height growth following intensive silvicultural treatments[J]． Forest Science，2001,47( 3):287-300.

[12] 符利勇，孙华.基于混合效应模型的杉木单木冠幅预测模型[J].林业科学，2013，49(8)：65-74.

[13] 陆昕，胡海清，孙龙，等.大兴安岭地表细小死可燃物含水率预测模型[J].东北林业大学学报，2016，44(7)：84-90.

[14] 陈东升，孙晓梅，李凤日.基于混合模型的落叶松树高生长模型[J].东北林业大学学报，2013，41(10)：60-64.

邢俊景，女，1989年11月生，东北林业大学理学院，硕士研究生，E-mail：973063328@qq.com。

曲智林，东北林业大学理学院，教授。E-mail：q_zhilin@nefu.edu.cn。

2016年12月20日。

S762.1

1)林业公益性行业科研专项(201404402)。

责任编辑：王广建。

Ground Surface Fuel Moisture Content by Mixed Effects Models in Daxing’an Mountains//Xing Junjing, Qu Zhilin(Northeast Forestry University, Harbin 150040, P. R. China)//Journal of Northeast Forestry University，2017,45(3)：58-62.

A real-time fuel moisture prediction model with the mixed effects was built with nonlinear mixed effect model (NLMEM) and stand factors as the stochastic effect. The fuel moisture model was with 288 sets of data related to the fuel moisture which were collected from three typical forests includingLarixgmelinii,QuercusmongolicaFischer and mixture ofLarixgmeliniiandBetulaplatyphylla. This model can solve the problems of heteroscedasticity by adding more weights to the residual variance. The results show that the fitting effect of the real-Time NLME prediction model (MAE=0.716 7,MRE=0.026 6) with the random effects and heteroscedasticity are better than that of the model (MAE=0.815 6,MRE=0.031 2) without considering the random effects. Moreover, the accuracy of the model (AIC=547.72, BIC=581.29, -2LL=527.72) using a constant plus power function as the heteroscedastic structure is the highest, and it is obvious superior to the real-time NLME prediction model (AIC=961.65, BIC=988.50, -2LL=945.65) without adding more weights to the residual variance. The results from the model test by using independent samples show that the test precision of the NLME model (MAE=0.495 8，MRE=0.034 2) with the random effects, and heteroscedasticity structure has some improvements in comparison to the multivariate nonlinear regression model (MAE=0.588 5,MRE=0.588 5) fitted by the least square method. The real-time fuel moisture content prediction model based on the mixed effects method can well describe the change laws in fuel moisture content for different types of forest in the regional scale of interest.