室温下表面极化效应对量子点带隙和吸收峰波长的影响∗
2017-08-07程成王国栋程潇羽
程成 王国栋† 程潇羽
1)(浙江工业大学应用物理系,杭州 310023)
2)(Departm ent of Chem istry,Tem p le University,Philadelph ia PA 19122,United States)
室温下表面极化效应对量子点带隙和吸收峰波长的影响∗
程成1)王国栋1)†程潇羽2)‡
1)(浙江工业大学应用物理系,杭州 310023)
2)(Departm ent of Chem istry,Tem p le University,Philadelph ia PA 19122,United States)
(2017年3月20日收到;2017年4月27日收到修改稿)
对于离散在本底介质中的纳米晶体量子点,考虑表面极化效应,通过像电荷法建立极化势能项,应用微扰法求解激子的薛定谔方程,得到了与本底介电系数直接相关的量子点带隙解析表达式.对不同本底中尺寸依赖的量子点带隙、第一吸收峰波长、第一吸收峰波长移动进行的计算表明,表面极化效应对量子点的带隙和第一吸收峰波长有明显的影响.随着本底介电系数的增大,量子点的带隙减小,第一吸收峰波长红移.量子点在不同本底中的第一吸收峰波长移动会在某个固定粒径达到最大值,最大值对应的粒径取决于量子点种类.
量子点,表面极化效应,带隙,吸收峰波长
1 引 言
纳米晶体量子点(nanocrystal quantum dots, QDs)由于量子尺寸效应、表面效应等,使得其具有独特的光电性质,这些独特的光电性质在光电子器件中有很大的应用潜力,近年来得到了人们的广泛关注[1].
实验表明,量子点的带隙不仅与其尺寸有关,温度和本底介质都会对量子点的带隙产生影响.温度对量子点带隙的影响来源于两个方面:热膨胀和电子-声子耦合效应,带隙随温度的变化可以用Varshni定律来描述[2].另一方面,量子点通常离散在本底介质中,由于量子点的介电系数与周围本底材料的介电系数不同,会在两者的界面产生表面极化效应,或介电受限效应[3].由于表面极化效应的存在,相同尺寸的量子点处于不同本底介质中时,其带隙会发生移动,导致其吸收峰和辐射峰的中心波长发生偏移,这会对量子点光纤放大器、量子点激光器等光电子器件的设计和研究产生明显影响.
Brus等[4,5]用有效质量近似,研究了量子点的带隙,通过解激子的薛定谔方程给出了激子基态能量的表达式,即Brus方程,该方程隐含背景材料介电系数对量子点带隙的影响,但无法直接进行计算.后来,人们对Brus方程进行空间电荷修正,提出了修正的Brus方程[1],但修正的Brus方程无法反映本底介电系数的影响.Takagahara等[6-8]研究了量子阱和量子点的表面极化效应,用有效质量近似计算了包含表面极化的激子能量,引入了与介电系数比有关的两个复杂系数A0和A1,用来反映量子点的表面极化强弱.他们发现表面极化效应增强了激子束缚能和跃迁振子强度,并得出维数越低,表面极化效应越明显的结论.近年来,文献[9,10]研究发现表面极化对Si量子点的荧光特性有重要影响.Rodina和Efros[11]总结了各种纳米结构的表面极化效应的影响,并研究了纳米结构中激子吸收和发射的极化特性.如上所述,迄今为止,人们无法直接得到由表面极化效应引起的量子点带隙的变化,或无法分析背景材料对量子点带隙的影响,使得计算结果与实验观测有差距.根据近年来的实验观测,在不同本底材料中,即使是相同尺寸的量子点,它们的带隙和吸收峰波长都会发生变化,而人们经常需要定量评估这种变化.因此,提供一种简洁明了的关于量子点表面极化效应的解析表达式是十分必要的.
本文引入像电荷的概念处理表面极化效应.在激子的哈密顿量中加入了电子、空穴和镜像电荷之间的相互作用势能,通过微扰法求解激子的薛定谔方程,得到了包含表面极化效应的量子点带隙表达式,给出了量子点带隙与本底介电系数之间的关系.实例计算了不同粒径的PbSe量子点在正己烷和UV胶本底中的带隙、第一吸收峰值波长.分析了PbSe量子点带隙、第一吸收峰波长随本底介电系数的变化规律,并阐明了其本质机理.研究了不同本底中量子点的第一吸收峰波长移动随尺寸的变化,得到了第一吸收峰波长移动最大值对应的粒径.由本文首次得到的量子点带隙关联于本底介电系数的解析表达式,可深入了解本底材料对量子点带隙的影响,直接确定量子点依赖于本底介电系数的带隙和第一吸收峰波长的移动,有助于量子点光谱特性的实验研究和量子点光电子器件的设计.
2 理论模型
量子点的带隙能是产生电子-空穴对所需的最小能量,它决定了量子点的光谱特性[12].量子点纳米颗粒通常离散在本底介质中(甲苯、正己烷、玻璃、UV胶等),由于量子点与本底材料的介电系数不同,其产生的表面极化效应会对量子点的带隙产生影响.研究表面极化效应的方法通常是根据表面极化电荷分布来求解极化势能,该方法比较复杂且无法得到直接计算量子点带隙的表达式.此外,也可引入像电荷的概念,用电子、空穴和像电荷之间的相互作用来代替表面极化效应对电子和空穴的影响[1].像电荷法的优点是可以用电荷间的相互作用势能简单方便地表示出极化势能,并得到量子点带隙的具体表达式.本文采用像电荷法.
2.1 像电荷的大小和位置
大多数量子点的形状近似为球形.考虑粒径为R、介电系数为ε1的球形量子点嵌入介电系数为ε2的均匀本底介质中.由于量子点很小,本底介质可以近似看成无限大.将电子和空穴分开考虑,首先考虑电子的极化效应.通过计算量子点内的电势求出电子对应的镜像电荷的大小和位置,再按照相同的方法确定空穴对应的镜像电荷的大小和位置.
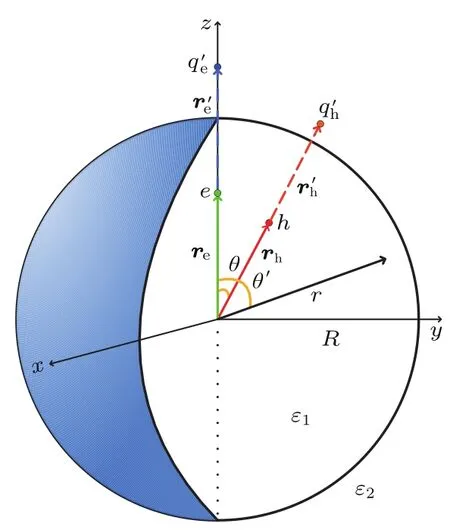
图1 量子点表面极化示意图Fig.1.Su rface polarization d iagram of quantum dot.
如图1所示,以通过量子点中心和电子所在点的直线为极轴,量子点的中心为原点,建立球坐标系,电子的位置矢量为re,则量子点内任意一点的电势满足泊松方程
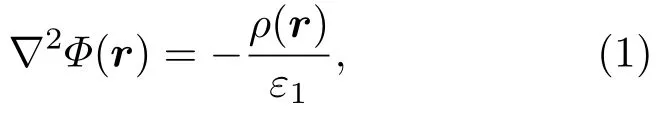
其中ρ(r)是电荷体密度,且ρ(r)=-eδ(r-re),r是任意一点的位置矢量;Φ(r)是位置r处的电势;ε是介电系数.由于系统具有轴对称性,因此在量子点内r/=re的位置,暂不考虑电子产生的电势,方程(1)可以写为如下形式:
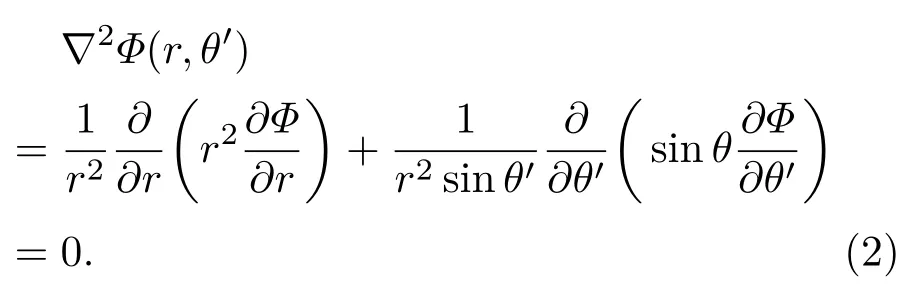
方程(2)的通解为
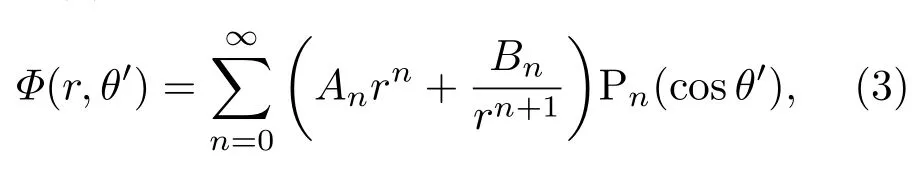
其中θ′是r与极轴的夹角;Pn(cosθ′)是n阶勒让德(Legendre)多项式;An和Bn是待定系数,可以通过边界条件确定.
在量子点内部,r=0处的电势φ(0)应为有限值,因此在量子点内1/rn+1的系数为0.考虑到电子在r位置处产生的电势为库仑势,将其中的1/|r-re|展开成勒让德多项式,可以得到量子点内除电子所在点之外任意位置的电势为
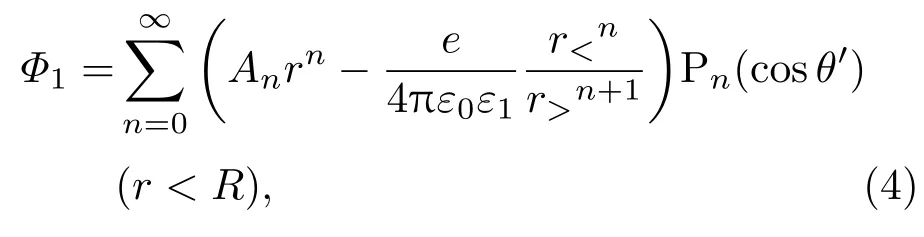
式中r<是r和re中较小的那一个,r>是r和re中较大的那一个.由边界条件r→∞时的电势为0,可知(3)式中rn的系数为0,量子点外部区域中任意位置的电势可以表示为
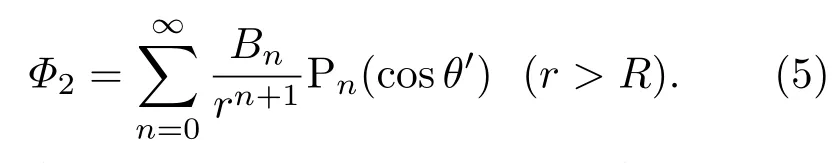
通过解泊松方程得到了量子点的内部区域和外部区域的电势,根据电势在电介质界面满足的边界条件,方程(4)和(5)中的待定系数为
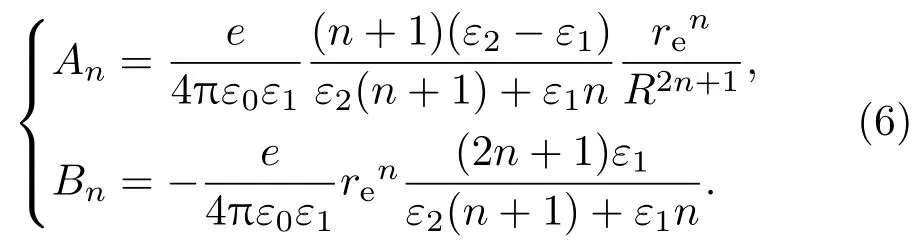
于是,量子点内除电子所在点外任意位置的电势为
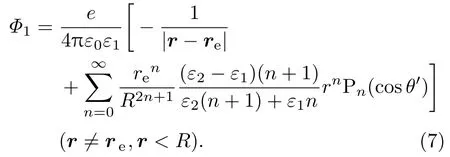
将(7)式中的勒让德多项式进行变换,得到更为简洁的形式:
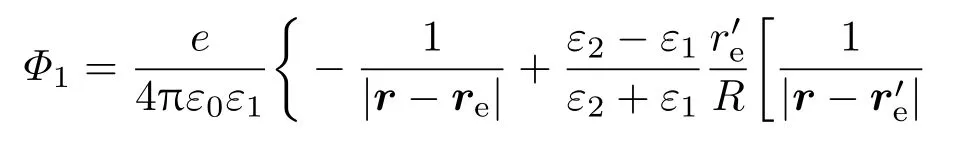
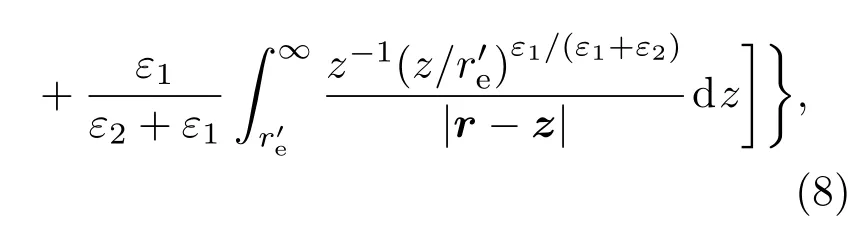
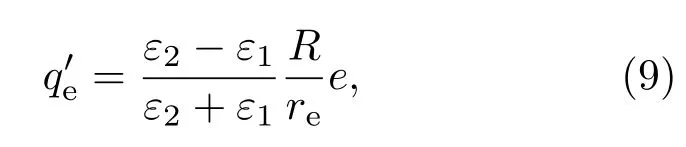
对于空穴所对应的镜像电荷的大小和位置,以经过量子点中心和空穴所在点的直线为极轴建立球坐标系,按照相同的方法得到空穴诱导产生的离散像电荷的大小为
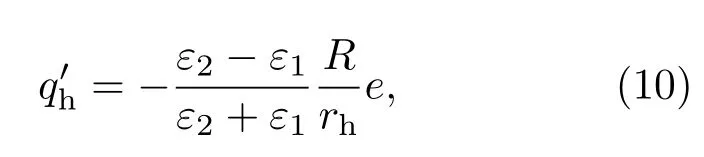
2.2 电子-空穴对的势能
考虑表面极化效应,电子-空穴对的势能应表示为电子、空穴和对应镜像电荷之间的相互作用势能
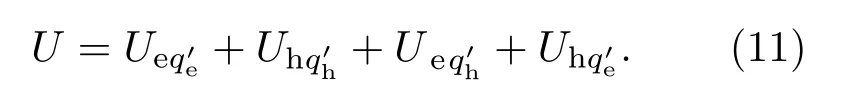
(11)式中,右边四项的下标分别表示电子与电子像电荷、空穴与空穴像电荷、电子与空穴像电荷、空穴与电子像电荷之间的相互作用势.具体如下:
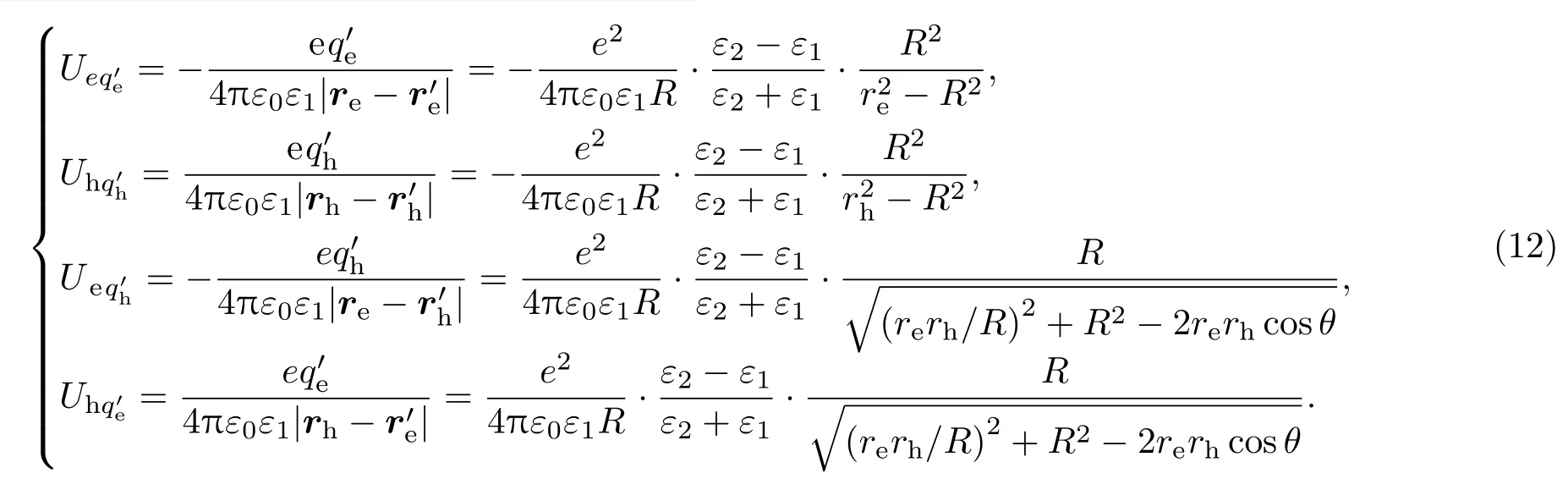
方程(12)中的θ是re和rh之间的夹角.因此激子势能U的具体形式为

2.3 量子点的带隙
根据有效质量近似[1]得到电子和空穴的动能,加上包含表面极化效应的势能项,得到量子点中激子的哈密顿量 ˆH.把势垒看成无限大,则量子点中激子的薛定谔方程为
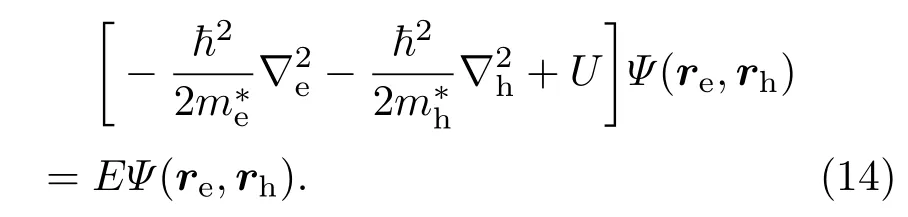
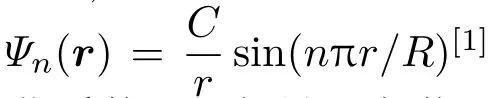
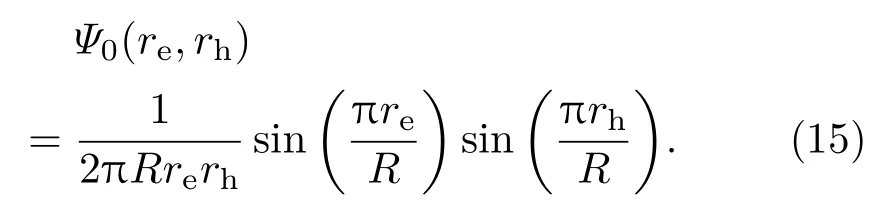
在量子尺寸约束较强的情形下(量子点的粒径R小于激子玻尔半径,例如荧光波长位于近红外波段的PbSe量子点等),电子、空穴和像电荷之间的相互作用势能比较小,可以把激子哈密顿量中的相互作用势能项看成微扰(当量子点的粒径远大于激子玻尔半径时,则不能将其视为微扰).因此激子哈密顿量可以写成H=H0+H′,H0是电子和空穴的动能之和,H′是相互作用势能项.能量本征值E按照微扰展开为E=E0+E1.利用波函数Ψ0(re,rh)求解H0的能量本征方程,得到能量本征值E0为电子-空穴的动能之和.
对于一级微扰能量本征值E1,根据微扰理论E1= 〈Ψ0(re,rh)|H′|Ψ0(re,rh)〉,利用波函数Ψ0(re,rh),并令a=re/R/=1,b=rh/R/=1,得到
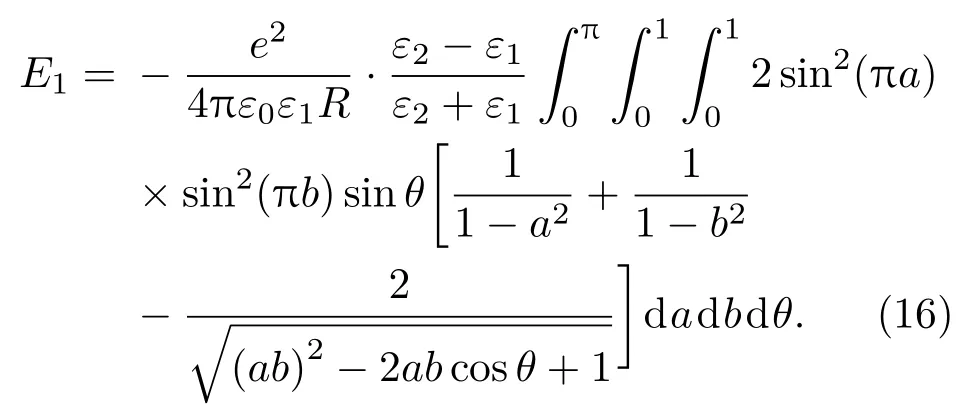
在(16)式中θ=0时,a/=b;当a=b时,θ/=0.对上式进行数值积分得到
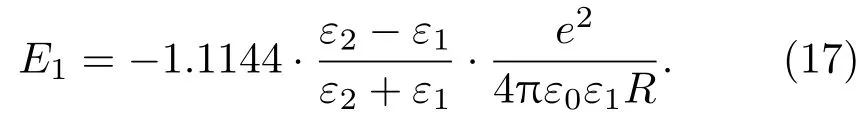
将能量本征值E加上体材料带隙以及库仑作用项[1],得到本底介质中量子点的激子的基态能量或带隙为
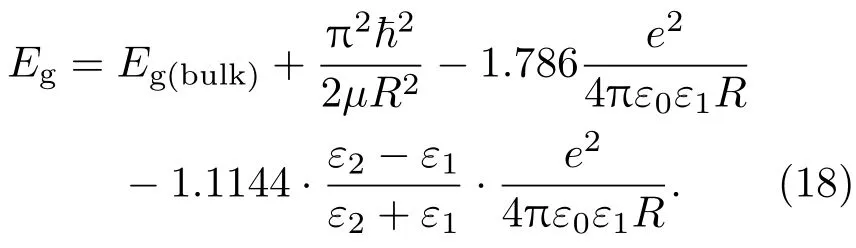
(18)式右边的第一项Eg(bulk)是对应体材料的带隙,第二项是受量子尺寸约束的激子的动能(折合质量1/µ=1/m∗e+1/m∗h,其中m∗e,h为电子和空穴的有效质量),第三项为电子-空穴的库仑作用势,第四项为由表面极化效应引起的极化势能项,它表征了介电系数为ε1的量子点处于介电系数为ε2的本底介质中时,其带隙和吸收峰值波长发生的偏移.作为比较,这里给出Brus方程[4]:
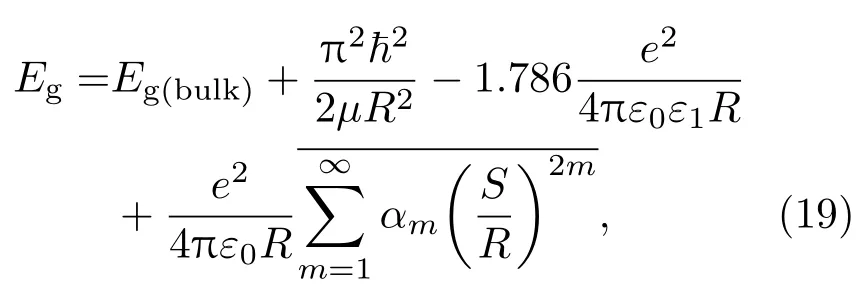
上式右边的前三项与(18)式相同,且与本底材料无关;第四项是极化势能项,其中αm=(ε-1)(m+ 1)/[ε1(εm+m+1)](ε=ε1/ε2,m是求和变量), S是电子、空穴的位置,上面的横线表示对整个波函数求平均.第四项关联于本底介电系数,但很难直接计算出来.后来,人们对(19)式进行了空间电荷修正,提出了修正的Brus方程[13]:
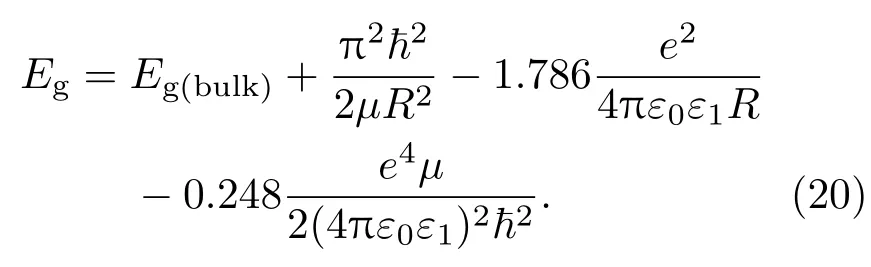
方程(20)右边的第四项空间电荷修正与前三项相比较,量值很小(约为第二项的1%[14]),且与本底材料无关,或者说修正的Brus方程无法描述本底材料对带隙的影响.相比较,本文得到的(17)或(18)式,直观地反映了表面极化效应对带隙影响的本质机理,其系数是ε1和ε2的函数,代入参数后可以进行直接计算,因此,是一个可用来明确分析本底材料对带隙影响的简单直观的解析表达式.
3 计算结果与讨论
下面利用方程(18)对常用的几种量子点,如II-VI族CdSe,IV-VI族PbSe,PbS量子点进行实例计算.通过实例计算,具体对比研究本底介质中表面极化效应引起的量子点带隙移动和第一吸收峰值波长移动随量子点种类、尺寸和本底介质的变化.
3.1 不同本底中量子点的表面极化效应
图2给出了不同本底的介电系数ε2对PbSe, PbS和CdSe量子点的带隙和吸收峰值波长的影响,计算选取的三种量子点的直径都为4 nm,量子点的相对介电系数、激子玻尔半径aB、常温下体材料的带隙Eg等参数列于表1.
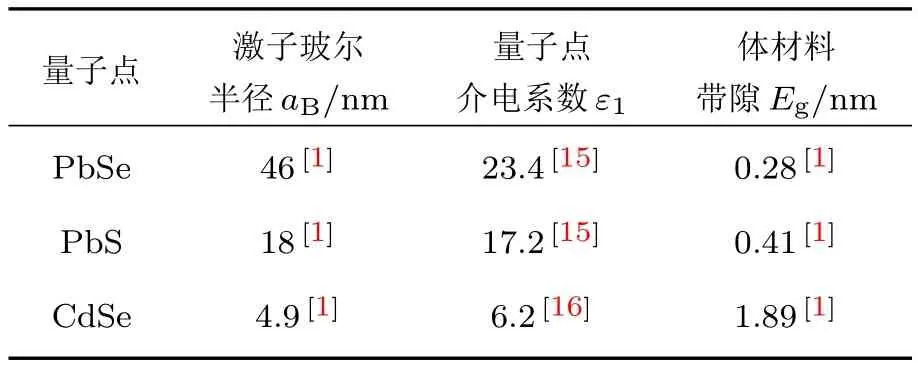
表1 PbSe,PbS和CdSe量子点的参数Tab le 1.The param eters of PbSe,PbS and CdSe QDs.
由图2可见,随着本底介电系数的逐渐增大,量子点的带隙逐渐减小.原因如下:当本底介电系数ε2<ε1(量子点介电系数)时,电子、空穴与各自像电荷的符号相同,ε2越小,表面极化效应越强,激子的束缚能越大,量子点的带隙能越大,从而使得量子点的带隙产生蓝移.当ε2=ε1时,界面处的表面极化效应消失,本底介质对量子点的带隙没有影响.当ε2>ε1时,电子、空穴与各自像电荷的符号相反,随着本底介电系数ε2增大,表面极化效应增强,但是量子点的带隙减小,从而使量子点带隙红移.本质上,表面极化效应对量子点带隙的影响取决于电子、空穴诱导产生的像电荷的电荷分布及正负符号(方程(9),(10)).
作为比较,人们研究了在外加电场作用下量子点中激子的斯塔克能移,给出了激子吸收峰波长随外加电场方向和强度的变化,其行为表现出向较低光子能量移动[17].这种变化是由外电场产生的,与本文讨论的量子点与本底介电系数不同而产生的固有的极化电场有很大的区别.在本文中,表面极化场的大小和方向是由本底介电系数和量子点内电子、空穴的分布决定的,通常比较小.然而,在外电场作用下产生的表面极化场在某些情况下可以很大,例如文献[18,19]中提出的GaN/InN/GaN和GaAs/Ge/GaAs“三明治”层状量子阱结构中,由于界面处两种半导体原子间的相互作用以及应变产生的压电极化,使得在界面处产生了很强的极化场,从而使带隙减小,甚至使能带结构反转.
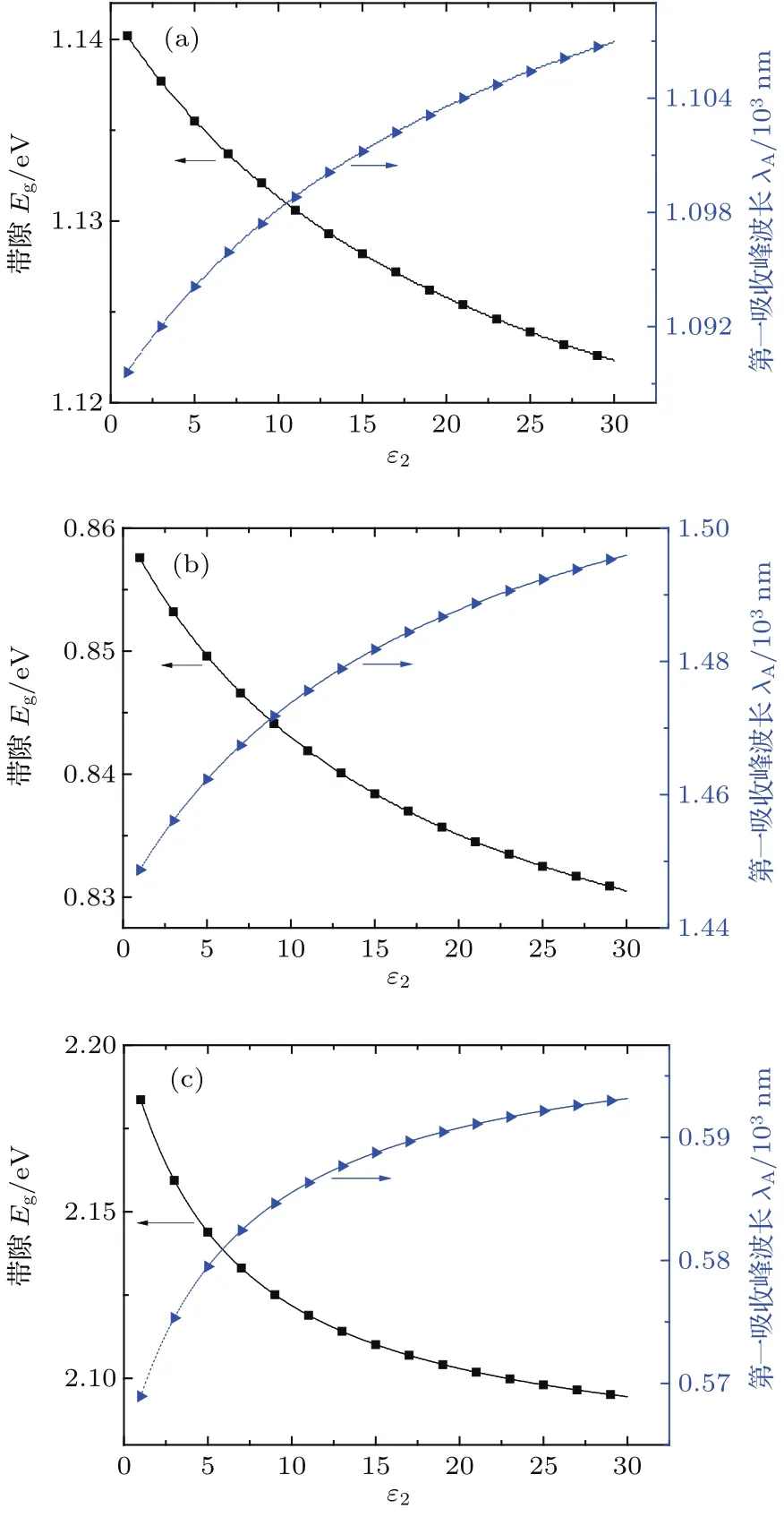
图2 本底材料介电系数对(a)PbSe,(b)PbS,(c)CdSe量子点的带隙和第一吸收峰波长的影响Fig.2.The bandgap and the fi rst absorp tion-peak wavelength of(a)PbSe,(b)PbS and(c)CdSe QDs varying with relative d ielectric coefficient of background m edia.
将量子点从一种本底转移到另一种本底,带隙会发生偏移.在实验中,人们主要关注第一吸收峰值波长的偏移.下面以真空(ε2=1)中量子点的第一吸收峰波长为参考,计算不同本底中量子点第一吸收峰波长的相对偏移,研究其随本底相对介电系数ε2和粒径R的变化.计算选取PbSe,PbS,CdSe三种量子点,结果如图3所示.
由图3可见,对某一粒径的量子点,本底介质的介电系数越大,其第一吸收峰波长偏移(相对于真空中的第一吸收峰波长)也越大.不同粒径的量子点在相同的两种本底中转移时,第一吸收峰波长的偏移随着粒径逐渐增大,在某一粒径处达到最大值;当粒径继续增大时,偏移逐渐减小.值得指出的是,对给定种类的量子点,第一吸收峰波长的最大偏移ΔλA,max所对应的粒径是恒定不变的,该粒径与本底介质无关,而是由量子点本身的性质决定的.根据表1中的参数,可计算得到最大偏移对应的粒径R=12.1 nm(PbSe),7.3 nm(PbS),2.9 nm (CdSe).
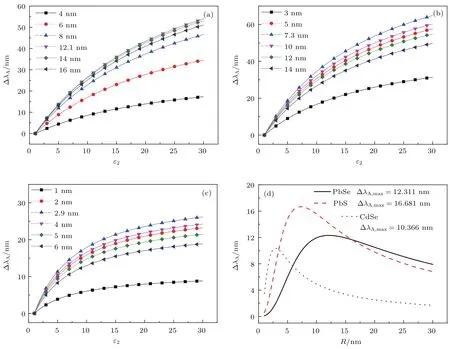
图3 (a)PbSe,(b)PbS和(c)CdSe量子点第一吸收峰波长偏移随本底相对介电系数(ε2=4.5)和(d)随粒径的变化Fig.3.The fi rst absorp tion-peak wavelength shift of(a)PbSe,(b)PbS and(c)CdSe QDs varying with relative dielectric coefficient of background m ed ia(ε2=4.5)and(d)d iam eter of QDs.
实验上,文献[20],[21]分别给出了甲苯(ε2= 2.37[20])和四氯化碳(ε2=2.2[21])本底中PbS量子点的第一吸收峰波长.本文的结果与这两组实验数据对比,相同尺寸的量子点在不同本底中的第一吸收峰值波长有偏移,并且随着本底介电系数的增大,量子点的第一吸收峰值波长红移,变化趋势与图2的结果一致.在高浓度掺杂的情况下,由于量子点表面基团之间的相互作用,会使得量子点第一吸收峰波长进一步红移,相关的讨论已经超出本文范畴,不再详述.
3.2 不同尺寸量子点的表面极化效应
对于PbSe量子点离散分布于正己烷溶剂(ε2=1.58[20])和UV胶(ε2=4.04[1])中,由(18)式可得PbSe量子点的带隙如图4所示.PbSe量子点的相对介电系数、激子玻尔半径aB、常温下体材料的带隙Eg列于表1.
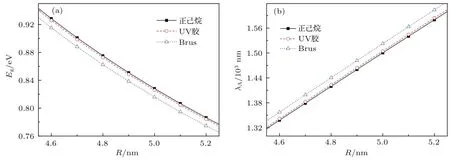
图4 尺寸依赖的PbSe量子点在正己烷和UV胶本底中(本文)以及由B rus方程计算的(a)带隙和(b)第一吸收峰波长Fig.4.The diam eter dependent(a)bandgap and(b)the fi rst absorption-peak wavelength of PbSe QDs doped in hexane,UV-gel in this paper,and B rus equation.
从图4(a)可见,与真空情况的Brus方程相比,本底介电系数对量子点带隙的影响很大,在粒径4.6-5.2 nm的范围内,两者相差Eg≈0.132 eV.但本底为正己烷和UV胶的量子点的带隙基本相同,这是因为PbSe量子点的介电系数很大,从正己烷转移到UV胶,本底介电系数的变化相对较小.进一步,我们可以通过带隙来研究表面极化效应对量子点第一吸收峰波长的影响,结果示于图4(b).由图可见,第一吸收峰值波长随量子点尺寸的增大而增大,变化趋势近似成线性,且不同本底中量子点的第一吸收峰波长有偏移.
一般而言,通过测量同一粒径的量子点在不同本底中的第一吸收峰波长,可对理论计算结果进行验证.但是由于实验室中的量子点样品都有一定的粒度或尺寸分布,一般可达5%[22,23].量子点带隙对尺寸很敏感,微小的粒度偏差造成的吸收峰值波长偏移都会掩盖掉本底变化引起的偏移.因此,对不同本底中量子点的吸收峰值波长偏移,在实验室中很难进行准确的验证.精确的方法应该是通过单个量子点在不同本底中的吸收峰值波长进行验证,也可以通过粒径高度一致的量子点样品进行验证.
4 结 论
介质本底中量子点的表面极化效应会对量子点的带隙和第一吸收峰值波长产生较为显著的影响.本文用通过求解量子点内的电势得到了像电荷的大小和位置,建立了极化势能项,用微扰法求解激子的薛定谔方程,得到与本底介质相对介电系数有关的基态能量表达式.该解析表达式直观反映了表面极化效应对量子点带隙的影响.
用该表达式计算了不同本底中尺寸依赖的量子点的带隙、第一吸收峰波长.计算结果表明,表面极化效应对量子点带隙的影响,本质上取决于电子-空穴诱导产生的像电荷的符号和大小,当本底的介电系数ε2小于(或大于)量子点的介电系数ε1时,表面极化效应使量子点的带隙蓝移(或红移),随着本底介电系数的增大,量子点带隙总体呈现红移.量子点在不同介质本底中的第一吸收峰波长移动会在某个粒径达到最大值,最大值对应的粒径大小取决于量子点的种类,对PbSe,PbS和CdSe量子点,该粒径分别为12.1,7.3,2.9 nm.
本文得到的量子点带隙随本底介电系数的变化,对量子点光谱特性的实验研究和量子点光电器件的设计有重要意义.
[1]Cheng C,Cheng X Y 2017 Nanophoton ics and Applications of Quan tum Dots(Beijing:Science Press)pp3-69 (in Chinese)[程成,程潇羽2017量子点纳米光子学及应用(北京:科学出版社)第3-69页]
[2]Narayanaswam y A,Feiner L F,M eijerink A,van der Zaag P J 2009 ACS Nano 3 2539
[3]Zhou Y J,Rabe K M,Vanderbilt D 2015 Phys.Rev.B 92 041102
[4]B rus L E 1984 J.Chem.Phys.80 4403
[5]Tyrrell E J,Sm ith J M 2011 Phys.Rev.B 84 165328
[6]Takagahara T 1993 Phys.Rev.B 47 4569
[7]Pereira T A S,de Sousa J S,Freire J A K,Farias G A 2010 J.Appl.Phys.108 054311
[8]Slachm uylders A F,Partoens B,M agnus W,Peeters F M 2006 Phys.Rev.B 74 235321
[9]E l-Kork N,Huisken F,von Borczyskow ski C 2011 J. Appl.Phys.110 074312
[10]Lyu Y R,Hsieh T E 2013 J.Appl.Phys.113 184303
[11]Rodina A V,E fros Al L 2016 J.Exp.Theor.Phys.122 554
[12]M urphy C J 2002 Anal.Chem.74 520A
[13]Pejova B,Grozdanov I 2005 M ater.Chem.Phys.90 35
[14]Cheng C,Yan H Z 2009 Phys.E:Low Dim ension.Syst. and Nanostruc.41 828
[15]Hyun B R,Chen H,Rey D A,W ise FW,Batt C A 2007 J.Phys.Chem.B 111 5726
[16]W ang L W,Zunger A 1996 Phys.Rev.B 53 9579
[17]Chang K,X ia J B 1997 So lid State Comm um.104 351
[18]M iao M S,Yan Q,van de W alle C G,Lou W K,Li L L, Chang K 2012 Phys.Rev.Lett.109 186803
[19]Zhang D,Lou W K,M iao M S,Zhang S C,Chang K 2013 Phys.Rev.Lett.111 156402
[20]Cheng C,Li J J 2017 Acta Opt.Sin.37 01300011(in Chinese)[程成,李婕婕2017光学学报37 01300011]
[21]Ushakova E V,Litvin A P,Parfenov P S,Fedorov A V, A rtem yev M,Prudnikau A V,Rukh lenko ID,Baranov A V 2012 ACS Nano 6 8913
[22]Cheng C,Li Z W 2016 Acta Opt.Sin.36 02160011(in Chinese)[程成,李志伟2016光学学报36 02160011]
[23]K um ar S,Biswas D 2007 J.Appl.Phys.102 084305
(Received 20 March 2017;revised manuscript received 27 April 2017)
Effects of surface polarization on the bandgap and the absorption-peak wavelength of quantum dot at room temperature∗
Cheng Cheng1)Wang Guo-Dong1)†Cheng Xiao-Yu2)‡
1)(Department of Applied Physics,Zhejiang University of Technology,Hangzhou 310023,China)
2)(Department of Chemistry,Temple University,Philadelphia PA 19122,United States)
The surface polarization energy that arises from the difference in dielectric coefficient between the quantum dot(QD) and the background m edium is investigated by the equivalent im age chargemethod.A generalexpression for the bandgap of QD depending on the dielectric coefficient of background m edium is presented by solving the exciton Schrödinger equation with the perturbation method.As exam p les,the sizedependent bandgaps,bandgap shifts,absorption-peak wavelengths and absorption-peakwavelength shifts of PbSe,PbS and CdSe QDs doped in different background media are determ ined in detail.There is evidence to show that the effects of surface polarization on the bandgap and the fi rst absorption-peak wavelength of QD are considerable.The bandgap decreaseswith the increase of dielectric coefficient of background m edium,which causes the absorption-peak wavelength to be red shifted.The effect of surface polarization on the bandgap depends substantially on the sign and value of image charge.W hen the dielectric coefficient of QD is greater than that of background m edium,the absorp tion-peak wavelength com es to blue shift due to surface polarization of QD.On the contrary,the absorption-peak wavelength com es to redshift.The absorp tion-peak wavelength shifts of QDs doped in different background media w ill reach amaximum in a certain diameter depending on the kind of QD.
quantum dots,surface polarization,bandgap,absorption-peak wavelength
PACS:78.67.Hc,73.20.At,71.35.-y,68.90.+g DO I:10.7498/aps.66.137802
∗国家自然科学基金(批准号:61274124,61474100)资助的课题.
†通信作者.E-m ail:1549769953@qq.com
‡通信作者.E-m ail:tug86157@tem p le.edu
PACS:78.67.Hc,73.20.At,71.35.-y,68.90.+g DO I:10.7498/aps.66.137802
*Pro ject supported by the National Natural Science Foundation of China(G rant Nos.61274124,61474100).
†Corresponding author.E-m ail:1549769953@qq.com
‡Corresponding au thor.E-m ail:tug86157@tem p le.edu
