基于伪相关函数的多级电平编码符号信号通用无模糊跟踪方法∗

刘桢 黄洁 王建涛 赵拥军 陈世文

(信息工程大学导航与空天目标工程学院,郑州 450001)

基于伪相关函数的多级电平编码符号信号通用无模糊跟踪方法∗

刘桢†黄洁 王建涛 赵拥军 陈世文

(信息工程大学导航与空天目标工程学院,郑州 450001)

(2017年3月13日收到;2017年4月11日收到修改稿)

针对新一代全球导航卫星系统(GNSS)中多级电平编码符号(MCS)信号存在的跟踪模糊问题,本文提出了一种通用的MCS信号无模糊跟踪方法.首先推导了不同MCS信号互相关函数的统一表达式,并给出了伪相关函数的定义;然后深入分析了实现无模糊跟踪需要满足的约束条件,推导了两路参考信号的通用构造方法以及相互之间的关系,为具体MCS信号的求解提供了极大的便利;进而给出了利用本文方法的GNSS接收机码跟踪环路模型.作为MCS信号的特例,分别讨论了本文方法在四种二进制偏移载波信号跟踪中的应用.仿真结果表明,本文方法能够有效解决MCS信号的跟踪模糊问题,具有良好的性能和广阔的应用前景.

全球导航卫星系统,多级电平编码符号,无模糊跟踪,伪相关函数

1 引 言

全球导航卫星系统(global navigation satellite system,GNSS)能够为全球范围内的用户提供全天候、全天时的定位、导航和授时(positioning,navigation and tim ing,PNT)服务,在国防、航空、金融以及气象等众多领域获得了非常广泛的应用,并展现出了巨大的军事价值和经济价值[1,2].如何获得更高精度的定位结果以及在十分有限的导航频段内实现资源共享已成为GNSS信号设计的核心问题,而解决这一问题的关键在于设计更优的扩频码片调制波形.目前,由于二进制偏移载波(binary off set carrier,BOC)[3,4]类信号和二进制编码符号(binary coded symbol,BCS)[5]信号的波形取值均为+1或-1,因而极大地限制了GNSS信号性能提升的空间,因此,多级电平编码符号(multilevel coded symbol,MCS)调制在GNSS信号设计领域得到了高度重视[6].由于MCS信号的波形符号可以任意取值,因而能够设计出最优的GNSS信号,如Galileo系统L1频点的复合BOC(composite BOC,CBOC)就属于MCS调制信号[7,8].MCS调制是目前最广泛的GNSS信号调制方式,BOC调制和BCS调制都属于它的特例,研究MCS调制对于我国北斗全球系统的信号设计具有重要的意义.但是与其特例BOC调制信号一样,MCS调制信号也存在码跟踪模糊的问题,引起模糊的根本原因在于自相关函数存在着多峰,造成主峰与边峰在时间和幅度两个维度上均难以区分,这就容易导致码跟踪环路错误锁定在边峰而不是主峰上,进而造成很大的伪距测量误差,这对于高精度的新一代GNSS是无法接受的.因此,需要研究MCS调制信号的通用无模糊跟踪方法.

近年来,对GNSS信号无模糊跟踪的研究已成为国内外导航信号处理领域的研究热点,提出了很多方法,但都是针对BOC信号.这些方法可分为三类：BPSK-like方法[9-11]、峰跳法(bump jum p, BJ)法[12,13]和边峰消除(side-peaks cancellation,SC)方法[14].BPSK-like方法最早由文献[9]提出,将BOC信号的上下两个边带信号视为与其具有相同码速率但调制在不同载波频率上的两个BPSK信号,并直接采用传统BPSK处理算法处理其中任一边带信号,成功消除了BOC信号自相关函数的多峰问题,且与传统接收机架构兼容.由于BPSK-like方法是一种频域滤波方法,需要复带通滤波器,文献[10]又提出了一种简化方法,但存在着0-2.5 dB的性能损失.文献[11]继续做出改进,用简化的滤波器对相关结果进行滤波,也可获得边峰消除能力,但是,该方法破坏了BOC信号自相关函数的窄主峰特性,损失了BOC信号的高精度定位优势.BJ方法在传统跟踪环路的基础上加入一组远超前(very early,VE)和远滞后(very late,VL)的相关器[12],辅助接收机检测对准支路是否锁定在主峰上,该方法不改变自相关函数的形状,只增加相关器的数量.文献[13]中提出了扩展的BJ算法,加入相关器的位置不再固定,而是与BOC信号的调制阶数和前端滤波有关.BJ方法非常适合处理如BOC(1,1)等低阶BOC信号,但是对于高阶BOC信号和低载噪比条件则不适用.

SC方法是一类方法的统称[14],该类方法的基本思想是：在接收机内部引入多个与接收信号不同的参考信号并与接收信号做互相关,然后通过这些互相关函数的线性或非线性组合合成一个无边峰的相关函数,理想的相关函数是实现稳健跟踪的关键[15].目前,边峰消除方法包括三种类型：自相关函数边峰消除方法(auto-correlation sidepeak cancellation technique,ASPeCT)[16],副载波相位消除(sub carrier phase cancellation,SCPC)方法[17,18]和伪相关函数(pseudo correlation function,PCF)方法[19-29].ASPeCT方法通过引入没有副载波调制的伪码信号与BOC(n,n)信号形成互相关函数[16],然后再将该互相关函数与BOC(n, n)的自相关函数进行平方相减,从而消除边峰的影响,但只适合于BOC(n,n)信号.SCPC方法[17]利用两路正交的参考信号分别与接收信号进行相关,然后通过平方相加消除多峰的影响,该方法适用于任意的BOC信号,文献[18]将其应用于Galileo系统E5信号的处理,该方法与BPSK-like方法拥有相同的优缺点.

PCF方法通过引入特别设计的本地码来生成一个主峰宽度与BOC信号自相关函数主峰相当的单峰相关函数,因此能够保留BOC信号的优点.文献[19]提出了适用于偶数阶SineBOC信号的方法,文献[20]对其做了改进,适用于奇数和偶数阶的SineBOC信号.文献[21]提出了适用于CosineBOC信号的PCF方法.文献[22]提出了一种适用于高价SineBOC信号的边峰消除方法.文献[23,24]对通用的BOC信号模型进行了研究,并基于该模型扩展了PCF方法的适用范围.但是,这些文献中提出的BOC信号通用模型形式上并不完全统一,不便于统一分析.文献[25]分析了BOC信号通用模型,提出了通用的边峰消除方法.文献[26]提出了非相干双鉴别函数方法,其中一路鉴别函数易于实现且抗多径性能好,但是码跟踪性能较弱,另一路鉴别函数的码跟踪性能好但是复杂度高,两路鉴别函数联合可以发挥各自的优势,该方法只适用于SineBOC信号的无模糊跟踪.文献[27]提出了BOC信号无模糊的捕获方法.文献[28]从信号分解的角度将接收BOC信号分解为若干个周期矩形脉冲信号后,分别与本地BOC信号和相应扩频码进行相关运算,最后通过组合处理去除边峰,但是接收信号的扩频码相位及码多普勒信息都未知,不可能对接收BOC信号进行分解,只有当码多普勒较小、每个矩形脉冲只进行单点采样时,才能够实现,所以这种方法的实现难度较大.文献[29]对其做了改进,通过分解参考信号实现.对于高阶调制BOC信号,需要分解的信号个数是调制阶数的2倍,复杂度很高.

上述研究结果是BOC信号无模糊处理领域的重要成果,但是由于BOC信号是特殊的MCS信号,不仅是双极性调制,波形取值矢量也对称,因而针对BOC信号的无模糊跟踪方法不适合于MCS信号.因此,本文研究基于伪相关函数的MCS信号通用无模糊跟踪方法,该方法在同一个接收机环路框架下,能够接收不同的MCS信号,因而可以简化接收机的设计.本文首先给出MCS信号的数学模型,然后分析边峰消除方法的设计思想,进而提出参考信号的通用构造方法,作为特例,该方法也适用于BOC信号,然后给出了该方法的码跟踪环路模型,最后进行了仿真实验.

2 MCS信号模型

目前的BPSK信号、BOC信号以及BCS信号中,BPSK和BOC属于BCS的特例,均要求波形取值矢量d的取值为{+1,-1},因而统称为双极性信号.对于GNSS接收机而言,采用双极性信号的一个明显优势是可以大大降低复杂度,但是对码片取值必须为{+1,-1}的约束极大地限制了GNSS信号性能提升的空间.如果进一步放开这一约束条件,允许波形取值矢量d任意取值,则可以设计出任意梯状波形的信号,这种信号就称之为MCS信号[6].一个扩频码周期T内,基带MCS调制信号的数学表达式为

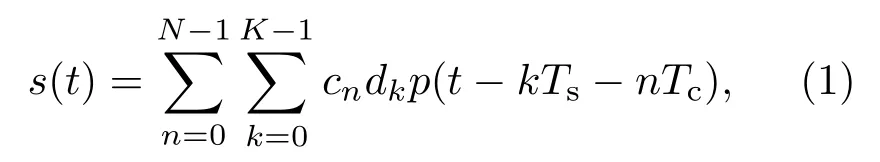
其中,N=T/Tc为扩频码长;Tc为单个扩频码码片时长;K为一个扩频码片包含的子码片个数；Ts=Tc/K为子码片时长;cn为二进制扩频码序列;d=[d0,d1,···,dK-1]为满足能量归一化条件

的波形取值矢量;p(t)为时长Ts的子码片矩形波形.扩频码速率为fc=1/Tc的MCS信号记为M CS([d0,d1,...,dK-1],fc)或M CS([d0,d1,···, dK-1],ρ),其中ρ=fc/f0,f0=1.023 MHz为基准频率.

现阶段GNSS信号均可以视为MCS信号,可以看出MCS信号是BCS信号的进一步扩展,与BCS信号的不同在于码片取值dk.通过放宽波形取值矢量d的取值,MCS信号的设计自由度大大增加,可以设计出满足不同需求的GNSS信号.近年来,越来越多的研究表明,在相同的扩频码速率下,通过对MCS信号的取值进行设计,可以获得更高的定位精度和抗多径性能[6].良好的性能和高的设计自由度使得MCS信号在新一代GNSS信号设计中受到广泛关注,并应用于新体制信号的设计,例如,Galileo E1 OS信号[7]所采用的CBOC信号就是一种典型的MCS信号[8].

3 通用无模糊跟踪方法设计

3.1 通用的伪相关函数推导

假设接收信号s(t)和参考信号s′(t)为两个扩频码速率都为fc的MCS调制信号,波形取值矢量分别为d= [d0,d1,···,dK-1]和d′=,则其互相关函数Rss′(τ)定义为

将(1)式代入(2)式可得

扩频码cn和可认为是理想的伪随机序列,即满足以下形式的δ函数

如果cn和为两个不同的扩频码序列,则显然有

如果cn和为两个相同的扩频码序列,并且当pTs(t-kTs-nTc)和pTs(t-τ-k′Ts-n′Tc)存在重叠时,(3)式中的积分值不为零,经过化简后可得

定义中间变量rk为

从(6)式可以看出,Rss′(τ)为分段线性函数,所有的分段点均位于kTs处,此时的互相关函数值为

在相邻的两个分段点之间,Rss′(τ)为线性函数,由此可以得出,互相关函数Rss′(τ)的形状由分段点处的值rk决定,因而也被称为互相关形状点.对于GNSS接收机而言,接收信号s(t)的形式是确定的,因而可以通过改变本地参考信号s′(t)来改变互相关函数Rss′(τ)的形状.

为了获取无边峰的互相关函数,文献[19]中提出了一种基于伪相关函数的方法,虽然该方法只针对偶数阶SinBOC信号,但提供了一种很好的设计思想.该方法的原理是预先设计两路特殊的本地参考信号,将接收信号与这两路参考信号分别进行相关,然后对两路互相关函数进行非线性组合,就可得到一个无边峰的窄三角形状的函数,该函数被称为伪相关函数.设两路参考信号s′(t)和s′′(t)的波形取值矢量分别为d′和d′′,与接收信号的互相关函数分别为Rss′(τ)和Rss′′(τ),定义伪相关函数如下：

对于GNSS接收机而言,为了彻底消除捕获和跟踪阶段的模糊性,要求相关函数(τ)的形状必须是对称的三角形状,同时保留自相关函数的窄主峰优势,这些要求可描述为以下三个约束条件

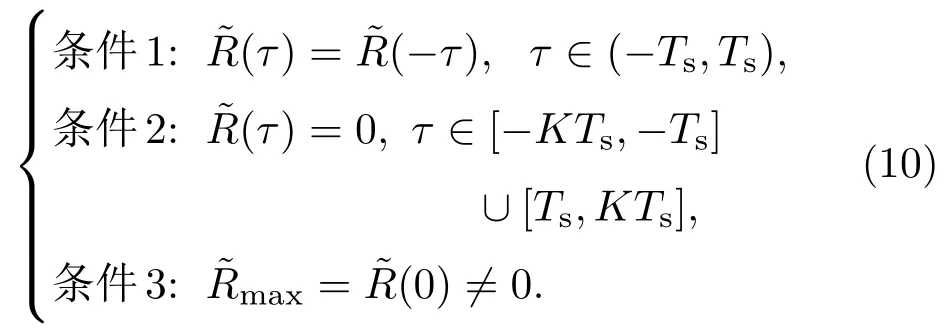
对于(10)式中的条件1,虽然当Rss′(τ)和Rss′′(τ)都为偶函数或都为奇函数时即可满足,但是却无法获得波形取值矢量d′和d′′之间需要满足的关系.容易证明,当两个互相关函数满足(11)式的条件时,伪相关函数也为偶函数,这是一个充分条件.

将(11)式代入(9)式后可得

根据Rss′(τ)的分段线性特性和(8)式,从(13)式可得到分段点处相关值r′k需要满足的一个约束条件为

(14)和(15)式就是(13)式的充分条件,将(7)式展开后可以得到的具体形式为

(16)式中,接收信号s(t)的波形取值矢量d=[d0,d1,···,dK-1]已知,根据(14)式和(15)式的约束条件,可以求出参考信号s′(t)的波形取值矢量].需要注意的是,(15)式中约束条件方程是非线性的,对于一般MCS信号的波形取值矢量,无法求出显示解,只能采取迭代的方式求出数值解.在求得参考信号s′(t)的波形取值矢量的基础上,下面讨论参考信号s′′(t)的波形取值矢量的求解方法,根据(11)式和(8)式可以得到

将(18)式整理为矩阵的形式可以得到

令

则(19)式可以写为以下形式：

对于MCS调制信号,波形取值矢量d中的元素dk均为非零值,因此,矩阵DΔ为可逆矩阵,进而可求得d′′的表达式为

根据(17)式可以得出参考信号s′(t)和参考信号s′′(t)的两个形状点取值向量满足r′=-r′′,将其代入(21)式中可得

将(16)式中k≥0的上半部分整理为以下的矩阵形式

(25)式清晰地反映了两路参考信号的波形取值矢量d′′和d′之间的关系,在求得d′之后便可很容易的求解出d′′,由于波形取值矢量还需要满足以下的能量归一化条件

因此,在对参考波形取值矢量d′和d′′能量归一化后,可分别求出与接收信号的互相关函数Rss′(τ)和Rss′′(τ),最后根据(9)式求出伪相关函数(τ).

以上讨论了任意MCS调制信号的PCF构造方法.BCS调制作为MCS调制的特例,也适用于上述方法,BOC调制作为BCS调制的特例,同样也适用于该方法.由于MCS信号和BCS信号的波形取值矢量没有任何规律,因而对于具体的信号,都需要利用该方法进行完整的求解.但BOC信号的波形取值矢量存在一定的规律,可以得到更简化的形式.因此,下面讨论BOC信号的PCF设计.

3.2 BOC信号PCF设计

BOC(m,n)信号根据副载波相位的不同分为SinBOC和CosBOC,而调制阶数Φ=2m/n又包括偶数和奇数两种情况,因此,BOC信号可分为四种类型. 但是根据波形取值矢量d=[d0,d1,...,dK-1]的对称性,BOC信号分为以下两种情形：

1)奇对称

包括偶数阶SinBOC和奇数阶CosBOC,此时

2)偶对称

包括奇数阶SinBOC和偶数阶CosBOC,此时

下面求解参考信号的波形取值矢量d′和d′′,以奇对称为例,通过观察(16)式可以发现,r′kr′-k可以表示为

对于(29)式的表示形式,根据(27)式的已知条件,可将(14)式的约束条件转化为以下形式：

同理,可求出偶对称类型下的结果为

结合(26)式中的能量归一化条件,另外,借鉴文献[19]中的思想,引入控制参数α∈[0,1),最后得到两种类型下的结果分别为：

至此,针对四种不同类型的BOC调制信号,分别构造出了两路参考信号的波形取值矢量d′和d′′.下面分别求解不同类型下的伪相关函数(τ).

将(35)式和(36)式代入(6)式中,并令p= τ/Ts-k,对于∀τ∈[kTs,(k+1)Ts),p∈[0,1).因此,可得到互相关函数Rss′(τ)和Rss′′(τ)的表达式分别为

以上讨论了偶数阶SinBOC的情况,对于其他三种BOC信号类型具有同样的结果.从(42)式可以看出(τ;α)为对称的单峰三角函数,完全消除了边峰,其最大值h(α)和底部宽度w(α)的表达式为

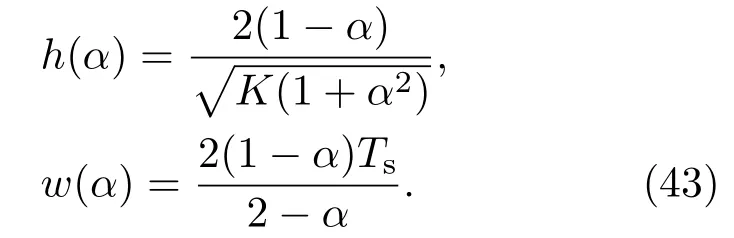
从(43)式可以看出,最大值h(α)和底部宽度w(α)均受控制参数α的影响,根据文献[17],α的典型取值为0或0.3.由于α∈[0,1),因此hPCF和 wPCF的范围分别为和(0,Ts].通过与BOC信号的自相关函数比较,可以得出以下结论：

4)伪相关函数方法彻底解决了BOC信号自相关函数的多峰问题,对于GNSS信号的无模糊处理具有非常重要的现实意义.

3.3 跟踪环路设计

图1给出了基于伪相关函数的码跟踪环路模型,可以看出,MCS信号的跟踪环路与BOC信号的跟踪环路没有明显区别[17],这也说明接收机是通用的,主要区别在于生成的参考信号不同.

图1中,超前和滞后支路的四个积分结果分别送入伪相关函数生成器后,进行如下的非线性组合

因此,码鉴别器的输出结果为

图1 基于伪相关函数的码跟踪环路模型Fig.1.Code tracking loop model based on pseudo correlation function.

对于MCS信号,由于无法得出伪相关函数的显示表达式,因而也就无法得到码鉴别器输出的显示表达式.对于BOC类信号则可以得出具体表达式,结合(42)式和(43)式,可得到码鉴别的结果为

4 仿真分析

仿真信号包括一般MCS信号和特殊MCS信号,一般MCS信号的波形取值矢量可以任意设置,仿真中仅以d=[2,-1,4,1]为例,特殊MCS信号选取已在新一代GNSS系统中应用的MBOC信号和BOC信号.MBOC信号为Galileo系统E1频点的CBOC(6,1,1/11)信号,调制阶数Φ=12,扩频码速率为fc=1.023 MHz,扩频码长为4092.偶数阶BOC信号包括：GPS系统L1和L2频点的M码信号、Galileo系统E6频点的PRS信号、E1频点的PRS信号以及北斗系统B3频点的民用信号B3C,它们分别采用SinBOC(10,5),CosBOC(10,5), CosBOC(15,2.5)和SinBOC(15,2.5)信号;奇数阶BOC信号包括：SinBOC(15,10)和CosBOC(15, 10)信号,Galileo系统的E5信号也可以看成是这两种信号的复合信号.BOC信号的扩频码长均为10230;控制参数α=0.3.特殊MCS信号仿真中与SCPC方法进行比较,但由于SCPC方法不能用于一般MCS信号,因而对于一般MCS信号只能利用本文方法.

从图2可以看出,无论对于一般MCS信号还是特殊MCS信号,均得到了理想的伪相关函数,其底部宽度和幅度均小于自相关函数主峰的底部宽度和幅度,这是因为上述信号的调制阶数均大于等于6.需要注意的是,相对于SinBOC信号而言, CosBOC信号伪相关函数的底部宽度又减小了一半,原因在于相同的调制阶数下,CosBOC信号的波形取值矢量的长度是SinBOC信号的两倍.对于特殊MCS信号,虽然利用SCPC方法也可消除多峰问题,但是损失了原始信号窄相关主峰的优势,本文方法不仅能够用于各类MCS信号,同时也能保持窄相关主峰的优势,而窄相关主峰能够大大提高码跟踪精度.因此,本文方法具有突出的优势.上述仿真仅以个别信号为例,本文方法对任意的MCS信号均能取得同样的结果,具有良好的有效性和通用性.

5 结 论

本文针对MCS信号的跟踪模糊问题,通过构造两路特殊的参考信号,然后将接收信号与参考信号的两个互相关函数进行非线性组合,从而得到理想的伪相关函数,很好地保留了接收信号自相关函数的窄主峰优势,彻底解决了原始信号的跟踪模糊问题,之后给出了基于本文方法的码跟踪环路模型.作为MCS信号的特例,推导出了BOC信号的参考信号、伪相关函数的参数以及码鉴别器的输出结果表达式,对于具体信号的理论分析提供了极大便利.仿真结果进一步验证了本文方法的有效性和通用性.因此,本文方法对未来MCS信号接收机的研制具有重要的理论指导和实际应用价值.

图2 (网刊彩色)基于本文方法的M CS信号的相关函数 (a)MCS([2,-1,4,1],1);(b)M CS-CBOC(6,1,1/11);(c)SinBOC(10,5); (d)CosBOC(10,5);(e)SineBOC(15,2.5);(f)CosBOC(15,2.5);(g)SinBOC(15,10);(h)CosBOC(15,10)Fig.2.(color on line)Correlation functions of MCS signals based on this paper method:(a)M CS([2,-1,4,1],1);(b)MCSCBOC(6,1,1/11);(c)SinBOC(10,5);(d)CosBOC(10,5);(e)SineBOC(15,2.5);(f)CosBOC(15,2.5);(g)SinBOC(15,10); (h)CosBOC(15,10).

[1]Guo F 2016 Ph.D.Dissertation(Beijing:Tsinghua University)(in Chinese)[郭甫2016博士学位论文(北京:清华大学)]

[2]W ang S Z,Zhu G W,BaiW H,Liu C L,Sun Y Q,Du Q F,W ang X Y,M eng X G,Yang G L,Yang Z D,Zhang X X,Bi Y M,W ang D W,X ia J M,W u D,Cai Y R, Han Y 2015 Acta Phys.Sin.64 089301(in Chinese)[王树志,朱光武,白伟华,柳聪亮,孙越强,杜起飞,王先毅,孟祥广,杨光林,杨忠东,张效信,毕研盟,王冬伟,夏俊明,吴迪,蔡跃荣,韩英2015物理学报64 089301]

[3]Betz JW 2001 Navigation 48 227

[4]Sun Z X,Yu Y,Zhou F,Liu S Z,Q iao G 2014 Acta Phys.Sin.63 104301(in Chinese)[孙宗鑫,于洋,周锋,刘凇佐,乔钢2014物理学报63 104301]

[5]Hegarty C J,Betz JW,Said i A 2004 Proceedings of the National Technical M eeting of the Institute of Navigation San D iego,California,USA,June 7-9,2004 p56

[6]Zhang X M,Yao Z,Lu M Q 2011 Sci.China:Phys. M ech.54 1077

[7]Zhou Y L,W ang D P 2010 Telecomm un.Syst.50 21(in Chinese)[周艳玲,王代萍2010电讯技术50 21]

[8]Zitouni S,Rouabah K,Chikouche D,M ok rani K,A ttia S,Harba R,Ravier P 2016 Aerosp.Sci.Techno l.50 112

[9]M artin N,Leb lond V,Guillotel G,Heiries V 2003 Proceedings of the 16th In ternational Technical M eeting of the Satellite D ivision of The Institute of Navigation Portland,OR,USA,September 9-12,2003 p188

[10]Lohan E S,Burian A,Ren fors M 2008 In t.J.Satell. Comm un.N.26 503

[11]Benedetto F,G iunta G,Lohan E S,Ren fors M 2013 IEEE Trans.on Veh.Technol.62 1350

[12]Fine P,W ilson W 1999 Proceedings of the 1999 Nationa l Technical M eeting of The Institu te of Navigation San D iego,CA,USA,January 25-27,1999 p671

[13]M argaia D,Falletti E,Bagnasco A,Parizzi F 2014 Proceedings of 2014 7th ESA W orkshop on Satellite Navigation and European W orkshop on GNSS Signals and Signal Processing ESTEC Noordw ijk,Netherlands,Decem ber 3-5,2014 p1

[14]W ard P 2003 Proceedings of Institu te of Navigation Annua l M eeting Albuquerque,NM,USA,2003 p146

[15]Zhang T W,Yang K D,M a Y L,W ang Y 2015 Acta Phys.Sin.64 024303(in Chinese)[张同伟,杨坤德,马远良,汪勇2015物理学报64 024303]

[16]Ju lien O,M acabiau C,Cannon M E,Lachapelle G 2007 IEEE Trans.on Aerosp.Electron Sys.43 150

[17]Juang J C,Kao T L 2010 Proceedings of the 23rd In ternational Technica l M eeting of The Satellite D ivision of the Institute ofNavigation Portland,OR,USA,September 21-24,2010 p3251

[18]Shivaram aiah N C,Dem pster A G 2008 Proceeding of the European Navigation Conference Tou louse,France, April 23-25,2008 p186

[19]Yao Z,Cui X W,Lu M Q,Feng Z M 2010 IEEE Trans. on Aerosp.Electron Sys.46 1782

[20]Yao Z,Lu M Q,Feng Z M 2010 IEEE Trans.on W irel Comm un.9 577

[21]Chen H H,W ang R,Jia W M,Yao M L 2012 J.Syst. Eng.E lectron.34 1090(in Chinese)[陈辉华,王榕,贾维敏,姚敏立2012系统工程与电子技术34 1090]

[22]Yan T,Wei J L,Tang Z P,Qu B,Zhou Z H 2015W ireless Pers.Comm un.84 2835

[23]Chen H H,Ren JW,Yao M L 2012 J.Astronaut.33 1646(in Chinese)[陈辉华,任嘉伟,姚敏立2012宇航学报33 1646]

[24]Chen H H,Ren J W,Jia W M,Yao M L 2013 Acta Electron.Sin.41 1(in Chinese)[陈辉华,任嘉伟,贾维敏,姚敏立2013电子学报41 1]

[25]Ren J W,Yang G T,Jia W M,Yao M L 2014 Acta Aeronaut.Astron.Sin.35 2031(in Chinese)[任嘉伟,杨贵同,贾维敏,姚敏立2014航空学报35 2031]

[26]Yan T,W ei J L,Tang Z P,Qu B,Zhou Z H 2015 GPS So lut.19 623

[27]Zhang T Q,Jiang X L,Zhao J T,W ang J X 2017 J. E lectron.Inform at.Technol.39 451(in Chinese)[张天琪,江晓磊,赵军桃,王俊霞2017电子与信息学报39 451]

[28]Liu W,X i Y,Deng Z L,Jiao J C,Y in L 2015 China Comm un.12 86

[29]Zhang H L,Ba X H,Chen J,Zhou H 2016 Acta Aeronaut.Astronaut.Sin.37 1(in Chinese)[张洪伦,巴晓辉,陈杰,周航2016航空学报37 1]

[30]Jin S G 2012 G lobal Navigation Satellite System s:Signa l,Theory and App lications(Rijeka Croatia:InTech-Pub lisher)p72

(Received 13 March 2017;revised manuscript received 11 April 2017)

Generalized unambiguous tracking method based on pseudo correlation function for multi-level coded symbol modulated signals∗

Liu Zhen†Huang Jie Wang Jian-Tao Zhao Yong-Jun Chen Shi-Wen

(School of Navigation and Aerospace Target Engineering,Inform ation Engineering University,Zhengzhou 450001,China)

The global navigation satellite system(GNSS)signal m odu lation type plays a crucial role in determ ining the perform ancesofpositioning,navigation and tim ing(PNT)services.Currently,thebinary off set carrier(BOC)m odu lation signal and binary coded symbol(BCS)modulation signal are both bipolar signals,which greatly restrict the room of im proving the GNSS signal perform ance.Therefore,mu lti-level coded symbol(MCS)m odulation has received great attention in the field of GNSS signal design.The MCSm odulation is them ost extensive step-coded symbolm odu lation mode,where BOC modulation and BCS modulation are its special cases.Since the waveform symbol of the MCS m odulation signalcan be arbitrarily valued,the optim alGNSS signal can be designed.However,like the BOCm odu lation signal,the MCSm odulation signal also has the p roblem of ambiguous tracking,and then results in a large pseudo range measurement error,which is unacceptab le for the new generation GNSS with high accuracy.In recent years,the unambiguous tracking of GNSS signals has becom e a hot research sub ject in the navigation signal processing dom ain and many methods are p resented,and thosemethods can be divided into three categories:BPSK-likemethod,bum p jum p(BJ)method,and side-peak cancellation(SC)method.However,thesemethods are designed for BOC signal,and they are not suitable for MCS signal.

Therefore,in this paper we p ropose a general unambiguous tracking algorithm based on the pseudo correlation function(PCF),which is suitable for MCSm odulated signals.Firstly,the unitary expression of MCSm odulated signal based on waveform value vector is given,then the unitary formula of cross-correlation function for MCS signal is derived and the definition of PCF is given.Then the constraint condition which should be satisfied to realize unambiguous tracking is analyzed in dep th,and the universal constructing method of two reference signals and the relationship between each other are derived according to this constraint condition,which brings great convenience for solving the specifi c MCS signal.The code tracking loop model of GNSS receiver based on the p roposed method is illustrated.It is observed that the p roposed method can receive different MCS signals under the sam e receiver loop fram ework,and can sim p lify the design of the receiver while elim inating the tracking ambiguous prob lem.Finally,as a special case of MCS signal,the app lications of the proposed method in four kinds of BOC signals are discussed respectively,and then the waveform value vector of the reference signal and the unitary expression of code discrim inator are derived.Simu lation resu lts show that the p roposed method can effectively solve the ambiguous tracking prob lem of MCS signal,which has good perform ance and broad app lication prospect.

global navigation satellite system,multi-level coded symbol,unambiguous tracking,pseudo correlation function

PACS:91.10.Fc,84.40.Ua,89.70.-a DO I:10.7498/aps.66.139101

∗国家自然科学基金(批准号:61501513)资助的课题.

†通信作者.E-m ail:liuzheninform ation@163.com

PACS:91.10.Fc,84.40.Ua,89.70.-a DO I:10.7498/aps.66.139101

*Pro ject supported by the National Natural Science Foundation of China(G rant No.61501513).

†Corresponding author.E-m ail:liuzhenin form ation@163.com