用数值模式匹配算法高效仿真轴对称型散射体海洋可控源电磁响应∗

林蔺 焦利光 陈博 康庄庄 马玉刚 汪宏年

(吉林大学物理学院,长春 130012)

用数值模式匹配算法高效仿真轴对称型散射体海洋可控源电磁响应∗

林蔺 焦利光 陈博 康庄庄 马玉刚 汪宏年†

(吉林大学物理学院,长春 130012)

(2016年11月17日收到;2017年4月10日收到修改稿)

圆盘、球体以及球冠状体是地球物理研究中非常重要的一类散射类型.在海洋环境中,圆盘可以用于描述玄武岩基岩以及油气圈闭构造等电阻率异常体,而球冠可以近似描述某些基岩隆起或起伏地形等.这类散射体的一个重要特征是其电阻率空间分布具有轴对称性.如果能够针对这类形状的散射体研究建立一套有效的海洋可控源电磁数值模拟方法,对于认识复杂地层条件下海洋电磁响应的变化特征、研究建立相关的资料处理和解释方法具有非常重要的意义.本文根据电导率轴对称分布特征,设法用一个或多个不同半径、不同厚度的水平同心圆盘逼近这类轴对称电导率散射体,并将这些同心圆盘与海洋环境中的空气、海水、沉积层和基岩等背景介质结合,形成一个在水平方向电导率具有轴对称分布、在垂直方向又具有分层特征的水平层状非均质模型.在此基础上,应用数值模式匹配法研究水平电偶极子天线电磁场的数值模拟方法,给出位于对称轴上的水平发射天线电磁场在层状非均质地层中的半解析解,建立海洋可控源电磁响应高效算法.最后通过数值模拟结果对该算法进行检验并考察海洋可控源三维电磁响应特征.

海洋可控源电磁,轴对称散射体,数值模式匹配法,半解析解

1 引 言

自20世纪80年代以来,海洋可控源电磁法(marine controlled source electromagnetic system, MCSEM)已成为研究海洋地形及海底构造等重要的地球物理方法[1].由于MCSEM对海底高阻目标体的有效探测能力,海洋可控源电磁法已逐渐发展成为海洋油气资源勘探的有效手段[2-4],关于海洋可控源电磁数值模拟与响应特征的研究已成为当前重要的一项研究课题[5,6].经过几十年的发展,一维水平层状地层中电磁响应的解析法[7],二维和三维非均质地层中的有限元法[8,9]、有限差分法[10,11]、有限体积法[12]和积分方程法[13,14]等数值模拟技术在海洋可控源电磁响应研究中均得到研究与应用.从理论上说,三维有限元和三维有限体积法为解决任意复杂海洋地电条件下的可控源电磁响应数值模拟提供了有力手段,但这类数值模拟的效率往往较低,对网格划分也要求严格,特别是对于高频、大源距(6000 m以上)情况,由于其电磁强度往往很弱,导致计算精度明显下降[15].三维积分方程法是求解局部散射体电磁响应比较理想的选择,但由于涉及满元矩阵方程的求解,当散射体较大时需要求解的未知参数很多,给数值结果的准确计算带来极大困难.实际上,海洋可控源往往采用多频多源距测量方式,其在复杂情况下的精确模拟仍然面临着严峻挑战[11],特别是当模型中存在起伏地形和起伏边界时,由于起伏边界本身的不确定性,大大增加了可控源电磁响应的计算难度.

近期的相关研究表明,海洋电磁勘探中遇到的典型高阻探测目标是玄武岩、碳酸盐岩以及油气圈闭,这些目标体可以近似表示为水平盘状散射体[5,7].同样地,某些基岩隆起或海底起伏也可以用球冠状散射体加以描述.由于水平圆盘和球冠等散射体的电导率空间分布具有轴对称性,完全可以用一个或多个半径与厚度不同的水平同心圆盘加以逼近,如果将这些同心圆盘与海洋环境中的空气、海水、沉积层与基岩等背景介质结合在一起,将形成一个在水平方向具有轴对称分布、在垂直方向又具有分层特征的水平层状非均质电导率模型.本文以这种水平层状非均质地层模型为基础,设法将井中地球物理中广泛使用的数值模式匹配算法(NMM)[16-22]推广应用到海洋可控源电磁响应数值模拟中,建立海洋可控源三维电磁响应的一种新型高效算法,给出位于对称轴上水平电偶极子电磁场的半解析解,并用这种算法研究考察水平圆盘、球形电阻率散射体在基岩或海底具有球冠状起伏表面时海洋可控源电磁响应的变化特征.

2 基本原理

2.1 海洋地电模型与等效水平层状非均质地层

图1(a)是本文要首先研究考察的一种海洋可控源地电模型,模型中包含有空气层、海水、沉积层、基岩以及水平圆盘散射体和球冠型基岩隆起,其中,空气和海水电导率分别用σair和σsea表示,沉积层和基岩电导率分别为σsed和σbs,海水和沉积层厚度分别为hsea和hsed.沉积层中水平圆盘散射体的半径和厚度分别为adsk和hdsk,其顶面离海底距离为ddsk;而球冠状基岩隆起的高度为hcrn,其对应的球体半径为acrn.图1(b)是由空气、海水等组成的等效水平层状非均质模拟,水平层界面位置用dn(n=1,2,···,N+5)表示.其中,圆盘所在地层是非均质的,其电导率在柱坐标系下可以表示为如下的阶跃函数[16,19]：

球冠状基岩隆起部分被划分成N个等厚度的薄圆盘,各圆盘水平界面位置为d4+j= hsed-hcrn[1-(j-1)/N](j=1,2,···,N),各圆盘的半径根据球冠边界形状从上到下按公式逐渐增加：

图1 高阻圆盘散射体和球冠型基岩隆起形成的具有轴对称电导率分布的海洋地电模型(a)及其等价水平层状非均质地层(b)Fig.1.M arine geoelectricmodelwith axisymm etric conductivity d istribu tion includ ing both resistive d isk and spherical cap type bedrock up lift(a)and its equivalentmodel consisting of horizontal layered inhom ogeneous beds(b).

而每个圆盘所在的水平层状地层也是非均质的,其电导率也具有如下的阶跃函数形式：

而其他地层电导率是常数,可以表示为

因此,整个模型上电导率是轴对称分片常数函数,其空间分布为

2.2 M axw ell方程的分解

海洋可控源电磁响应的正演模拟实质上是求解如下M axwell方程[12]：

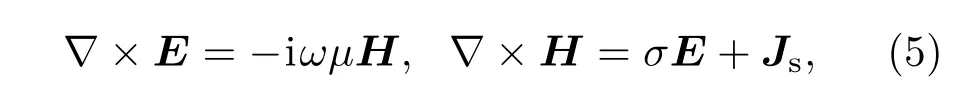
其中,σ=σ(ρ,z)是轴对称电导率函数,磁导率µ假定是常数,ω为发射信号的角频率且时间变化关系假定为eiωt.由于发射源工作频率很低,忽略了位移电流.为简单起见,假定发射源Js是一个单位强度的水平电偶极子发射天线且位于对称轴z上.利用直角坐标系与柱坐标系下单位向量间的变换公式和欧拉公式,可以将单位强度水平电流源展开成柱坐标系下的Fourier级数形式[16]：

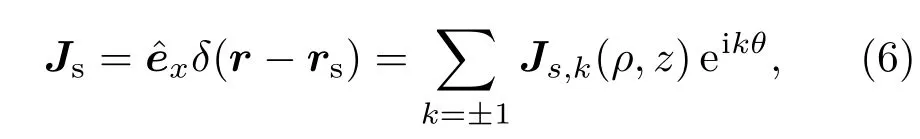
其中,

是柱坐标系下单位水平电偶极子源的k阶谐分量, ρs是足够小的常数(例如10-4m),保证在柱坐标轴附近电磁场仍然有界[16].

同样地,将方程(5)中的电磁场E = (σEρ,Eθ,Ez)T和H=(Hρ,Hθ,Hz)T展开成类似形式的Fourier级数：

将(6)和(7)式代入(4)式,并对方程进行分解,得到水平磁场的k阶谐分量HS,k=(Hρ,k,Hθ,k)T满足的方程[17,18,22]：

而右侧项是柱坐标系中的二维水平向量,其表达式为

为保证(8)式的解在z轴附近仍然有意义,引入如下第二类齐次边界条件[16,20]：

这里的ρMN是足够小的数(例如10-5m).由于存在趋肤效应,远处的电磁场快速衰减,所以在足够大外边界ρMX(例如105m)上,引入截断边界条件：

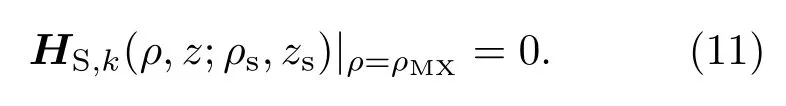
此外,水平电场分量ES,k=(σEρ,k,Eθ,k)T与水平磁场分量间具有如下关系[17]：

垂直电磁场分量可通过如下方程得到[16,17]：

2.3 海洋可控源电磁响应的半解析解

附录A中,通过数值模式匹配算法给出了完全柱状介质中方程(8)的求解过程以及相应的半解析解,同时通过方程(12)和(13)给出了计算其他电磁分量的方法与相应的半解析解,这些不含水平地层界面的半解析解称之为电磁场的基本解.为了得到图1(b)中水平层状非均质地层中的电磁场,需要分析海水中k阶水平磁场的基本解(入射波)的传播过程.当入射波传播到界面d1和d2时,将产生反射和透射,海水中界面d1附近的总场是入射场和上下界面反射场的叠加,因此可表示为[17,18,22]

等于下行波在界面d2上的反射,即

求解方程(16a)和(16b)可以得到

将(17)式代入(15)式中并经适当整理,得到发射源所在的海水中水平磁场k阶谐分量的半解析解：

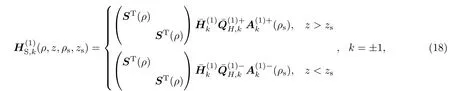
其中,

利用各个地层界面上电磁场的连续性条件,可以推导出地层n中的水平磁场k阶谐分量的半解析表达式[16,17]：

利用水平磁场分量的半解析解(19),(21)以及(12)式和附录A中的(A 10)式,可以得到各个地层上水平电场k阶谐分量的表达式[16,17].其中,发射源所在的海水中的电场可表示为

而在其他地层中电场具有如下类似的表达形式：

其中,

是地层n中水平电场k阶谐分量的传播矩阵.同样地,可以推导出电磁场垂直分量的半解析解[16,17],其中,在发射源所在的海层中：

而在其他地层n中：

将上面的关于电磁场水平分量与垂直分量结合起来,最后得到各个地层n中电磁场k阶谐分量的半解析表达式：

其中,上式右端出现的上标“±”分别表示接收点位于发射源的上部或下部.

进一步,将方程(29)和(30)代入方程(7)就可以计算出单位水平电流源在各个地层中任意位置产生的电磁场,换言之,通过解决两次二维问题,就可以得到层状非均质地层中水平电流源产生的电磁场,从而大幅提高了数值模拟的计算效率.

3 数值模拟结果

本节首先利用图1中地电模型,分别设计出水平层状地层和含有圆盘的水平层状地层两个不同的简化地电模型,并用传输线法(TLM)[7]以及三维有限体积法(3D FV)[12]分别计算这两个地电模型上可控源电磁响应,通过与上述NMM的数值结果进行对比,检验NMM的计算精度与效率.然后,通过NMM研究高阻圆盘与基岩隆起地电模型上海洋可控源电磁响应,在本节的最后部分,利用NMM进一步考察球形散射体与基岩凹陷以及球形散射体、基岩凹陷和海底隆起这两个地电模型的海洋电磁响应.

图2 水平层状海洋地电模型NMM和TLM法计算得到的主测线上电磁水平分量(Ex和Hy)的振幅与相位曲线对比(a)Ex振幅曲线;(b)Ex相位曲线;(c)Hy振幅曲线;(d)Hy相位曲线Fig.2.Com parison of the in line magnitudes(M VO)and phases(PVO)versus off set of electrom agnetic(EM) horizontal com ponents(Ex and Hy)ob tained by two d iff erent algorithm s of NMM and TLM in an horizontal layered m arine geoelectric model:(a)MVO of Ex;(b)PVO of Ex;(c)MVO of Hy;(d)PVO of Hy.

在整个数值模拟过程中,径向求解区间的变化范围为ρMN=10-4m和ρMX=5×104m,总节点数M+1=181,且所有节点ρα(α= 1,2,···,M+1)均按对数等间距增加.空气层、海水、沉积层电导率分别为σair=10-6,σsea=3.33和σsed=0.667 S/m;基岩和圆盘(或球体)的电导率分别为σbs=0.05和σdsk=0.01 S/m;海水层厚度为hsea=1000m.单位强度水平电流源位于z轴上且在海底上方50m处即b=-50m,发射源工作频率假定为0.25和0.75 Hz,而接收器均匀分布在海床面上,水平间距为200 m.收发距的变化范围为-6400m到6400m.

3.1 算法检验

首先,假定图1(a)中圆盘厚度和顶部离海底距离的分别是hdsk=150 m和ddsk=925 m,且沉积层厚度为hsed=2000 m.为了进行TLM与NMM数值结果的对比,进一步假定图1(a)中圆盘的半径adsk趋近于无限大,并且基岩与沉积层电导率相同,即σsed= σbs=0.667 S/m,这时图1(a)简化为由空气、海水、沉积层、高阻薄层以及沉积层组成的5层水平层状模型,因此可以用TLM进行正演计算,图2是该简化模型上由TLM与NMM计算得到数值模拟结果的对比.图2(a)和图2(c)分别是主测线上电磁场水平分量Ex,Hy的振幅与偏离距(magnitude versus off set,MVO)曲线,图2(b)和图2(d)是主测线上Ex,Hy的相位与偏离距(phase versus off set,PVO)曲线,其中实线是NMM数值结果,而离散符号是TLM数值结果.从图2可以看出,两种方法计算得到的电磁场数值结果均符合得很好.电磁场振幅的最大相对误差仅为2.65%,NMM的计算精度达到了TLM的水平.

图3 含圆盘状散射体的水平层状海洋地电模型中由NMM和3D FV计算得到的主测线上电磁场水平分量(Ex和Hy)振幅与相位曲线对比 (a)Ex振幅曲线;(b)Ex相位曲线;(c)Hy振幅曲线;(d)Hy相位曲线Fig.3.Com parison of the in line MVO and PVO of EM horizontal com ponents(Ex and Hy)obtained by two d iff erent algorithm s of NMM and 3D FV in the horizontal layered m arine geoelectric model with a resistive d isk: (a)MVO of Ex;(b)PVO of Ex;(c)M VO of Hy;(d)PVO of Hy.

为了进一步考察非均质层状海洋地电模型中NMM算法的计算精度,假定图1(a)中圆盘半径adsk=2000m,基岩与沉积层电导率仍然相同,形成一个具有不同厚度的5层水平层状非均质地电模型.图3是该模型分别用NMM法与3D FV法得到的主测线上Ex,Hy的MVO与PVO曲线对比结果,其中,实线与虚线是NMM计算结果,而离散的符号是3D FV数值结果.两种不同方法计算得到的数值结果同样符合得较好.图3中两个频率、65个接收点的数值结果,在HP Z820(Intel®CPU E5-2697 V 2 2.7GHz,256GB RAM)工作站上,NMM和3D FV所用CPU时间分别为5m in 57 s和65m in 3 s, NMM比3D FV所用时间少10倍以上,且NMM只占用0.536 Gb内存而3D FV需要的内存则达到35 Gb.因此,NMM在普通的PC机就可以运行,从而大大降低了计算成本.

3.2 含基岩隆起的水平圆盘响应

对于含有三维起伏界面的海洋地电模型可控源电磁响应的计算目前仍然是一项非常困难的工作,往往需要使用复杂的有限元技术才能加以解决.下面利用NMM法研究考察具有轴对称起伏地层边界情况下的海洋可控源电磁响应.

假定图1(a)中基岩电导率为σbs=0.05 S/m、基岩球冠隆起的高度hcrn=600 m、相应的球体半径acrn=3000 m,而圆盘参数、沉积层等参数与图3相同,从而形成一个含有圆盘与基岩隆起的海洋地电模型.数值模拟过程中,将基岩隆起划分成N=25个等厚度薄水平圆盘,图4是两个不同工作频率下计算得到的Ex和Hy的MVO与PVO曲线.对比图2、图3以及图4中的数值结果可以看到一个十分有趣的现象：Ex和Hy的MVO曲线均随源距增加而快速衰减、频率越高振幅衰减越快;由于基岩隆起的影响,在远场处,图4中Ex和Hy的振幅比图2和图3中的振幅更小.此外,不同地电模型上Ex和Hy的PVO曲线变化特征也相差较大.

图4 包含水平圆盘与基岩隆起模型的海洋地电模型上由NMM法计算得到的主测线上电磁场水平分量(Ex和Hy)振幅与相位曲线 (a)Ex振幅曲线;(b)Ex相位曲线;(c)Hy振幅曲线;(d)Hy相位曲线Fig.4.The in line M VO and PVO of both Ex and Hy ob tained by NMM in the horizontal layered m arine geoelectric model including both resistive disk and spherical cap type bed rock up lift:(a)MVO of Ex; (b)PVO of Ex;(c)M VO of Hy;(d)PVO of Hy.

为进一步了解可控源海洋电磁场的空间分布特征,图5(a)和图5(b)分别是xOz铅垂面上圆盘与基岩隆起周围的电场与电流密度实分量的向量图以及振幅灰度图.结果显示,电场与电流密度均随着源距增加而快速衰减,但在高阻圆盘内部与其边界周围以及高阻基岩隆起边界附近,由于积累面电荷影响,电场强度的振幅明显增大.但电流密度振幅与电场强度变化特征正好相反,由于积累面电荷对电流的排斥,导致高阻层中电流密度明显小于低阻层中的电流密度.此外,在高阻圆盘和高阻基岩隆起的边界附近,电场强度与电流密度的方向也产生了非常明显的变化.

图5 (网刊彩色)基岩隆起与水平圆盘周围电场强度与电流密度的实分量向量图与振幅灰度图 (a)电场(f=0.25 Hz);(b)电流密度(f=0.25 Hz)Fig.5.(color on line)The vector diagram and am p litude grayscale of real com ponents of electrical intensity(f=0.25 Hz)(a)and electrical current intensity (f=0.25 Hz)(b)in the horizontal layered m arine geoelectricmodel including both resistive d isk and spherical cap type bed rock up lift.

3.3 含基岩凹陷的高阻球体响应

图6是由球形散射体和球冠型基岩凹陷形成的海洋地电模型与其等价模型示意图,高阻球形散射体的半径和电导率分别为asph=700 m和σ=0.01 S/m,其中心到海床面距离dsph=750m,基岩凹陷对应的球冠高度和球体半径分别是hcrn=500 m和acrn=3000 m.模型中沉积层与基岩电导率与图1中模型完全相同,其值分别为σsed=0.667 S/m和σbs=0.05 S/m.在数值模拟中,将整个球形散射体和球冠基岩凹陷所在区域分别化分成N1=42和N2=25个等厚度薄层,并根据其边界位置用不同半径的薄水平圆盘加以逼近.图7是两个不同工作频率下Ex和Hy的MVO与PVO曲线.对比图7与图4的计算结果不难看出,两者差异很大.由于球形散射体的体积比圆盘大得多在加之存在基岩凹陷,导致Ex和Hy振幅随源距增加衰减更快,工作频率变化对振幅与相位的影响也更明显.

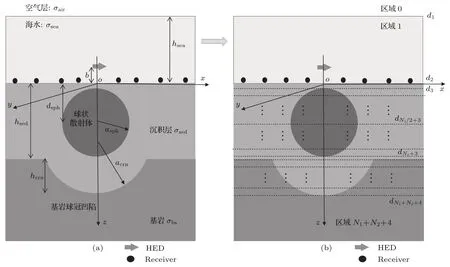
图6 由球形散射体和球冠基岩凹陷形成的海洋地电模型(a)与其等价模型示意图(b)Fig.6.M arine geo-electric model with a resistive spherical scatter and spherical cap type bed rock dep ression(a) and its equivalent model consisting of horizontal layered inhom ogeneous beds(b).

图7 球形散射体和球冠基岩凹陷模型上由NMM法得到的主测线上Ex,Hy的MVO与PVO曲线 (a)Ex振幅曲线; (b)Ex相位曲线;(c)Hy振幅曲线;(d)Hy相位曲线Fig.7.The in line MVO and PVO of both Ex and Hy ob tained by NMM in the horizontal layered m arine geoelectric model including both a resistive spherical scatter and spherical cap type bed rock dep ression:(a)MVO of Ex; (b)PVO of Ex;(c)MVO of Hy;(d)PVO of Hy.

图8 (网刊彩色)球形散射体和球冠基岩凹陷周围电场强度与电流密度的实分量向量图与振幅灰度图 (a)电场(f=0.25 Hz); (b)电流密度(f=0.25 Hz)Fig.8. (color on line)The vector diagram and am p litude grayscale of real com ponents of electrical intensity(f = 0.25 Hz)(a)and electrical cu rrent intensity(f=0.25 Hz) (b)in the horizontal layered m arine geoelectric model including both a resistive spherical scatter and spherical cap type bed rock dep ression.

图8(a)和图8(b)分别是xOz铅垂面上球形散射体和基岩凹陷周围的电场与电流密度实分量的向量图以及振幅灰度图.同样可以看到电阻率边界上积累面电荷对电场和电流密度空间分布的影响.在整个高阻球形散射体内部及其边界周围,电场强度明显增大,但在高阻球体内部电流密度明显减小,而在其边界周围附近电流密度明显增大.此外在基岩凹陷界面附近,也可以看到积累面对周围电场的影响,但由于受高阻球形散射体的屏蔽作用以及离发射源距离更远因素等影响,与球体散射体表面附近相比,其对周围电场的影响程度要小得多.

3.4 含海底隆起、基岩凹陷的高阻球体响应

图9 由球状散射体、球冠型海底隆起与基岩球冠凹陷组成的海洋地电模型(a)及其等价的水平层状非均质模型(b)Fig.9.M arine geo-electricmodelwith a resistive sphericalscatter,topography with spherical cap up lift and spherical cap bed rock dep ression(a)and its equivalent model consisting of horizontal layered inhom ogeneous beds(b).

图10 球状散射体、球冠型海底隆起与基岩凹陷组成的海洋地电模型上由NMM法得到的主测线上水平电磁场(Ex和Hy)的MVO与PVO曲线 (a)Ex振幅曲线;(b)Ex相位曲线;(c)Hy振幅曲线;(d)Hy相位曲线.Fig.10.The inline MVO and PVO of both Ex and Hy obtained by NMM in them arine geoelectric model including both a resistive spherical scatter,topography with spherical cap up lift and spherical cap bed rock dep ression: (a)MVO of Ex;(b)PVO of Ex;(c)M VO of Hy;(d)PVO of Hy.

为进一步考察海底地形中海洋电磁的响应特征,在图6地电模型的基础上,在海底面上增加一个高度hcrn1=300 m的球冠隆起,形成一个同时包含起伏海床面、高阻球形散射体、基岩凹陷等更加复杂的海洋地电模型,并且接收器按等水平距离放置在海床面上(见图9),而球冠对应的球体半径仍然为acrn=3000 m.此外,图9中的高阻球形散射体、基岩凹陷、沉积层和基岩电导率等参数与图6中的地电模型完全相同.在进行数值模拟时,将沉积层隆起、球形散射体和基岩凹陷分别划分成N1=25,N2=42和N3=25个等厚度薄层,形成一系列不同半径的薄水平圆盘.图10是两个不同工作频率下Ex和Hy的MVO与PVO曲线,不难看出由于起伏地形的影响,Ex和Hy的振幅与相位曲线与图7的结果差异十分明显,沉积层隆起导致Ex和Hy的MVO与PVO曲线变化范围明显减小.

图11(a)和图11(b)分别是xOz铅垂面上海底隆起、球形散射体和基岩凹陷周围的电场与电流密度实分量的向量图以及振幅灰度图.从图11同样可以看到海底隆起、球形散射体和球冠基岩凹陷边界上积累面电荷对整个电场强度与电流密度空间分布的影响.

图11 (网刊彩色)球状散射体、球冠型海底隆起与基岩凹陷组成的海洋地电模型上电场强度(a)与电流密度(b)的实分量向量图与振幅灰度图 (a)电场(f=0.25 Hz);(b)电流密度(f=0.25 Hz)Fig.11.(color on line)The vector diagram and am p litude grayscale of real com ponents of electrical intensity (f=0.25 Hz)(a)and electrical current intensity(f=0.25 Hz)(b)in them arine geoelectric model including a resistive spherical scatter,topography with spherical cap up lift and spherical cap bed rock dep ression.

4 结 论

针对海洋环境中广泛存在水平圆盘、球体、球冠等具有轴对称电导率分布的散射体,可用多个不同半径与厚度的水平薄圆盘加以逼近,将复杂的三维海洋地电模型转化为具有轴对称的水平层状非均质地电模型.利用电阻率空间分布的轴对称特征,可以将位于对称轴上的水平电偶极子天线电磁场正演模拟问题转化为两个轴对称问题加以求解,并通过数值模式匹配法可以得到海洋可控源电磁场的半解析解,实现海洋可控源三维电磁响应以及全空间电磁场的快速计算.

数值计算结果显示,对于水平层状地层模型,数值模式匹配法的计算精度可以得到传输线的水平;对于含有单一水平圆盘散射体模型,数值模式匹配法的数值模拟结果与3D FV算法符合得也很好,但数值模式匹配法算法效率和计算精度比3D FV算法更高,且占用的内存也更少.此外,圆盘、球体、海底隆起以及基岩隆起和凹陷等对可控源电磁勘探中的电场与电流密度空间分布均有非常明显影响,不同地电模型上Ex和Hy的MVO与PVO曲线往往差异巨大.在高阻散射体(圆盘、球体)内部与其边界周围以及边界隆起或凹陷界附近,由于积累面电荷影响,电场明显增强;但电流密度振幅与电场强度变化特征正好相反,积累面电荷对电流的排斥作用,导致高阻层内部电流密度明显减小.此外,在高阻散射体(圆盘、球体)与起伏地层边界上,电场强度与电流密度的方向也产生了非常明显的变化.

附录A无限厚层柱状非均质地层中电磁场的基本解

数值模式匹配算法的关键是需要事先确定每个地层(无限大均匀或柱状地层)中电磁场的基本解.为此,用有限长区间[ρMN,ρMX]逼近半无限区间,并将其剖分成M(偶数)个小区间,剖分节点位置用ρα(α=1,2,···,M+1)表示.选用二次New ton插值函数作为径向节点ρα上的基函数φα(ρ)(α=1,···,M)[16],根据方程(10)的第二类齐次边界条件以及方程(11)的截断条件,选择M个基函数组成列向量S(ρ)=(φ1(ρ),φ2(ρ),···,φM-1(ρ),φM(ρ))T,利用Petrov-Galerkin法将方程(6)中的±1阶水平磁场分量展开为如下形式[]:

求解(A 2)式可以得到2M个本征值κ2k,α和相应的本征向量Hk,α(α=1,2,···,2M).将本征值代入(A 3)式中并进行求解得:

进 一 步 求 解 方 程(A 4)可 确 定 向 量Ck=,其中,是本征向量矩阵.最后,我们得到无限大均匀或柱状地层中k阶谐变水平磁场分量的基本解[16]:

根据每个地层上电导率大小和空间分布,利用上面的方法可以计算出各个地层中本征值和本征向量矩阵和,从而确定每个地层的基本解.

此外,利用方程(12)和(14)可以得到水平电场分量的基本解

以及垂直电磁场分量的基本解

[1]Edwards N 2005 Surv.Geophys.26 675

[2]Constab le S 2010 Geophysics 75 75A 67

[3]Yuan J,Edwards N 2000 Geophys.Res.Lett.27 2397

[4]W eiss C J,Constab le S 2006 Geophysics 71 G 321

[5]Constab le S C,W eiss C J 2006 Geophysics 71 G 43

[6]Hoversten G M,Newm an G A,Geier A,Flanagan G 2006 Geophysics 71 G 239

[7]W ang J X,W ang H N,Zhou J M,Yang SW,Liu X J, Y in C C 2013 Acta Phys.Sin.62 224101(in Chinese) [汪建勋,汪宏年,周建美,杨守文,刘晓军,殷长春2013物理学报62 224101]

[8]Li Y G,Dai S K 2011 Geophys.J.In t.185 622

[9]Xu Z F,Wu X P 2010 Chinese J.Geophys.53 1931(in Chinese)[徐志锋,吴小平2010地球物理学报53 1931]

[10]Shen J S 2003 Chin.J.Geophys.46 280(in Chinese) [沈金松2003地球物理学报46 280]

[11]Streich R 2009 Geophysics 74 F95

[12]Zhou J M,Zhang Y,W ang H N,Yang SW,Y in C C 2014 Acta Phys.Sin.63 159101(in Chinese)[周建美,张烨,汪宏年,杨守文,殷长春2014物理学报63 159101]

[13]Chen G B,W ang H N,Yao J J,Han Z Y,Yang S W 2009 Acta Phys.Sin.58 1608(in Chinese)[陈桂波,汪宏年,姚敬金,韩子夜,杨守文2009物理学报58 1608]

[14]Chen G B,Wang H N,Yao J J,Han Z Y 2009 Acta Phys.Sin.58 3848(in Chinese)[陈桂波,汪宏年,姚敬金,韩子夜2009物理学报58 3848]

[15]Kong F N,Johnstad S E,Røsten T,W esterdah l H 2008 Geophysics 73 F9

[16]W ang H N,Tao H G,Yao J J,Zhang Y 2012 IEEE Trans.Geosci.Rem ote Sens.50 3383

[17]W ang H N,Tao H G,Yang SW 2008 Chin.J.Geophys. 51 1591

[18]Liu Q H,Chew W C 1992 Radio Sci.27 569

[19]W ang H N 2011 IEEE Trans.Geosci.Rem ote Sens.49 4483

[20]W ang H N,So P M,Yang SW,Hoefer W J R,Du H L 2008 IEEE Trans.Geosci.Rem ote Sens.46 1134

[21]Zhu T Z,Yang SW,Bai Y,Chen T,W ang H N 2017 Chin.J.Geophys.60 1221(in Chinese)[朱天竹,杨守文,白彦,陈涛,汪宏年2017地球物理学报60 1221]

[22]Chew W C 1990 W aves and Fields in Inhom ogeneous M edia(New York:van Nostrand Reinhold)

(Received 17 Novem ber 2016;revised manuscript received 10 April 2017)

Efficient simulation of marine controlled source electromagnetic responses for axisymmetric scatter by using numerical mode matching approach∗

Lin Lin Jiao Li-Guang Chen Bo Kang Zhuang-Zhuang Ma Yu-Gang Wang Hong-Nian†

(College of Physics,Jilin University,Changchun 130012,China)

Horizontal disk,sphere,and spherical crown are a very im portant type of scatter in geophysics research.In the marine environm ent,a disk-like scatter can be used to describe several resistive targets,e.g.,basaltic sills and stratigraphic hyd rocarbon reservoirs while spherical crown can be used to approximately depict the topography of interface for basem ent rock.This type of scatter has characteristics of axisymm etrical distribution of the conductivity. If som e app roaches can be established to efficiently simulate the m arine controlled source electrom agnetic(MCSEM) response to this scatter,it w ill be meaningful to investigate the nature of MCSEM responses in com p lex formation and to build app ropriate method of processing and explaining MCSEM data.In this paper,the resistive scatters are approximated by one or several horizontal concentric diskswith different radiiand thickness values,based on the axially symm etrical spatial distribution of conductivity.Then,a combination of these concentric disks with air,sea water and surrounding bedsw ill construct a horizontally stratified inhom ogeneous form ation with comm on axis-center,whose spatial distribution of conductivity is layered in the verticaldirection and axisymmetric in the horizontal direction.Based on the approxim ationsm entioned above,the com putation of MCSEM response excited by horizontal electrical dipole (HED)located at the z-axis is entirely transform ed into two axially symmetrical prob lem s for the Fourier harmonic com ponents of the electromagnetic(EM)fields.The differential operators about the horizontalmagnetic com ponents and transform ation of horizontal electrical com ponents and other EM com ponents from horizontalm agnetic com ponents are derived.Then,the num ericalm ode m atching approach is extended to the simulation of the EM field and threedimensional(3D)MCSEM responses excited by the HED in the formation.The p rocedure for solving the EM field is presented.The sem i-analytic solution of EM field in the whole space is obtained to efficiently and num erically model MCSEM response in the com p lex formation.Finally,the efficiency and accuracy of the presentmethod are demonstrated num erically.The characteristics of 3D MCSEM responses in three different cases are further investigated.

marine controlled-source electromagnetic method,axisymmetric scatter,numerical mode matching approach,sem i-analytic solution

PACS:91.25.Qi,02.30.Zz,41.20.-q DO I:10.7498/aps.66.139102

∗国家自然科学基金(批准号:41574110)和国家高技术研究发展计划重大项目(批准号:2012AA 09A 20103)资助的课题.

†通信作者.E-m ail:wanghn@jlu.edu.cn

PACS:91.25.Qi,02.30.Zz,41.20.-q DO I:10.7498/aps.66.139102

*Project supported by the National Natural Science Foundation of China(G rant No.41574110)and the National High-tech R&D Program,M ajor Pro ject,China(G rant No.2012AA 09A 20103).

†Corresponding author.E-m ail:wanghn@jlu.edu.cn