太赫兹互补金属氧化物半导体场效应管探测器理论模型中扩散效应研究∗

张镜水 孔令琴 董立泉 刘明 左剑 张存林 赵跃进†

1)(北京理工大学光电学院,北京 100081)

2)(首都师范大学物理系,北京 100048)

太赫兹互补金属氧化物半导体场效应管探测器理论模型中扩散效应研究∗

张镜水1)孔令琴1)董立泉1)刘明1)左剑2)张存林2)赵跃进1)†

1)(北京理工大学光电学院,北京 100081)

2)(首都师范大学物理系,北京 100048)

(2017年3月1日收到;2017年4月5日收到修改稿)

针对基于经典动力学理论传统模型中忽略扩散效应的问题,通过对基于玻尔兹曼理论的场效应管传输线模型的理论分析,建立了包含扩散效应的太赫兹互补金属氧化物半导体(CMOS)场效应管探测器理论模型,研究扩散效应对场效应管电导及响应度的影响.同时,将此模型与忽略了扩散效应的传统模型进行了对比仿真模拟,给出了两种模型下的电流响应度随温度及频率变化的差别.依据仿真结果,并结合3σ原则明确了场效应管传输线模型中扩散部分省略的依据和条件.研究结果表明:扩散部分引起的响应度差异大小主要由场效应管的工作温度及工作频率决定.其中工作频率起主要作用,温度变化对差异大小影响较为微弱;而对于工作频率而言,当场效应管工作频率小于1 THz时,模型中的扩散部分可以忽略不计;而当工作频率大于1 THz时,扩散部分不可省略,此时场效应管模型需同时包含漂移、散射及扩散三个物理过程.本文的研究结果为太赫兹CMOS场效应管理论模型的精确建立及模拟提供了理论支持.

互补金属氧化物半导体场效应管探测器,太赫兹,模型模拟,玻尔兹曼理论

1 引 言

随着太赫兹波技术在军事和民用各个领域的不断发展,研制高响应度、低噪声的太赫兹探测器成为相关科研领域的研究重点之一,而互补金属氧化物半导体(CMOS)场效应管太赫兹探测器因其成熟的技术、相对较低的成本及其他材料目前无法企及的良好性能(其最高响应度可达2.2 kV/W,等效噪声功率可达到而受到广泛的关注[1−5].为了减小探测器的制作成本,需要对设计好的探测器进行性能模拟测试,而该项工作的可信度依赖于太赫兹场效应管模型的精准程度,故精确的太赫兹场效应管探测器模型一直是国内外相关领域的重点研究方向[6−14].

目前常用太赫兹波段CMOS场效应模型为基于均匀电荷控制理论的线性电阻-电容-电感(resistance-capacitance-inductance,RCL)传输线理论模型.该模型运用1996年Dyaknov和Shur[15]提出的均匀电荷控制理论,通过经典动力学理论的一维德鲁德模型描述沟道内载流子的整体运动,并将其转变为由许多RCL单元组成的RCL传输线模型[16].目前针对基于该模型的理论研究只考虑载流子的漂移及散射运动,忽略了沟道内载流子浓度不均匀分布的扩散效应的影响.此外,关于扩散效应可省略的依据及条件并未见相关报道.

基于此,本文从玻尔兹曼理论出发,研究模型中扩散效应对太赫兹场效应管电导及响应度的影响.首先从玻尔兹曼电流方程推导出基于此理论的RCL模型方程,并通过与一维德鲁德RCL模型的对比,明确扩散效应在模型中的表达式.其次通过理论计算与模拟分析,分别得到静态与动态下两种不同理论的场效应管模型的响应区别,分析扩散效应对场效应管模型响应度的影响.同时,通过分析扩散效应随温度与频率的变化情况,结合3σ原则给出了扩散效应在模型中可省略的条件.研究结果为太赫兹CMOS场效应管探测器模型的精确建立提供了重要依据,并为其进一步技术及工程实现提供了关键理论及技术支持.

2 模型理论

现在的模型主要基于流体动力学中一维德鲁德模型,其主要包含漂移和散射效应.而玻尔兹曼方程则主要从非平衡态时的分布函数出发,推导出沟道的电流情况.故本节中通过对比二者之间的差异来说明扩散效应的重要性.

2.1 经典动力学传输线模型的基本形式

根据经典动能理论,沟道中的载流子运动可以用德鲁德模型来描述.基于该理论,对于沟道中电荷为q的电子,其动量p(x,t)为

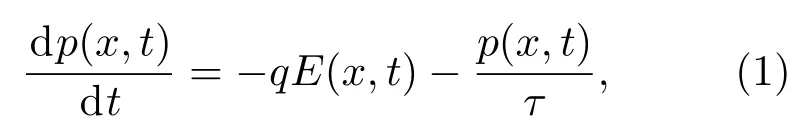
其中E(x,t)为沟道x处的电场大小;τ为有效电子散射时间,此处考虑声子作用与杂质碰撞.为了描述场效应管沟道中载流子的运动情况,Dyaknov和Shur[15]用经典动力学理论提出了一维德鲁德模型及粒子连续边界条件,

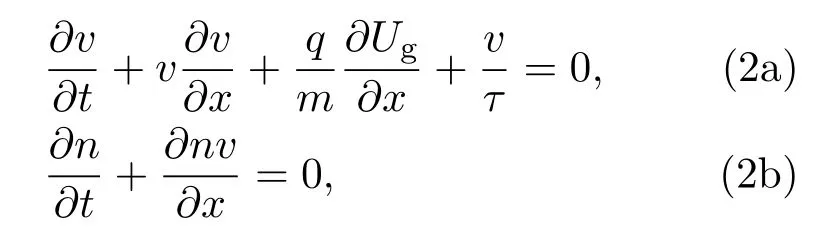
式中m为粒子的等效质量;n,v和Ug分别为沟道x处的载流子密度、载流子速度和栅极至沟道处的电压幅值大小.

若只考虑沟道内等离子体的基波与一次谐波,(2a)与(2b)式可以写成:

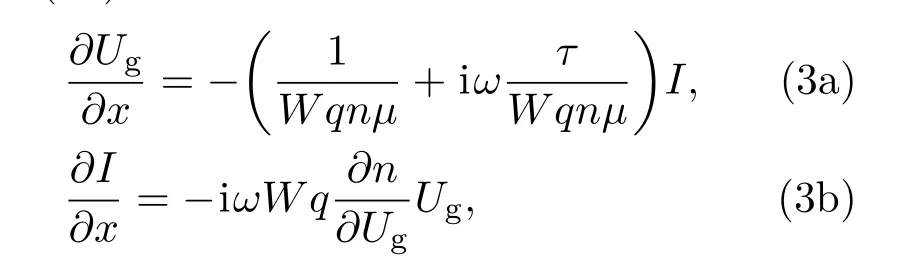
其中W为场效应管沟道宽度,µ为粒子迁移率,I是沟道内电流.(3a)和(3b)式与电报方程的基本形式一致,故沟道中载流子的运动实际可表示为RCL传输线模型,如图1所示.其R,L和C的阻抗表达分别为[16]

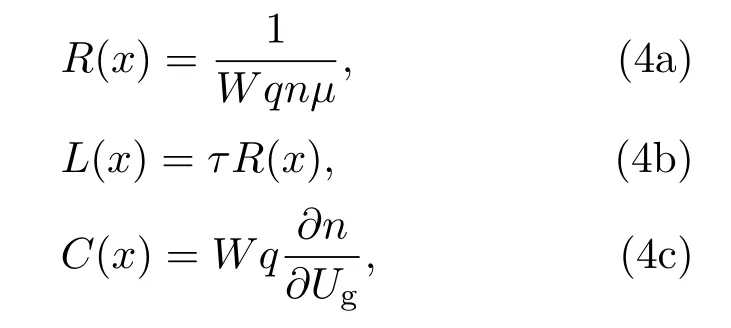
(4a),(4b)及(4c)式即为基于经典动力学理论的场效应管RCL传输线模型方程.运用该模型方程,场效应管沟道中载流子的运动可转化为如图1所示的模型.

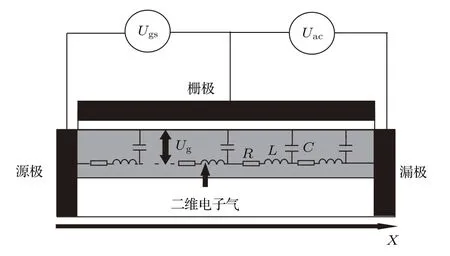
图1 场效应管沟道RCL传输线理论模型,其中Ug为栅极至沟道的电压差,Ugs为栅源极间所加直流电压,Uac为通过天线耦合进场效应管的太赫兹波;R,L和C的计算分别如(4a),(4b)和(4c)式所示Fig.1.The transmission line model for fi eld-electrictransistor in high frequency.Ugis the gate-to-channel local voltage,Ugsis the gate-to-source DC voltage,and Uacis the terahertz signal that coupled by the antenna.R,C and L are calculated with Eq.(4a),(4b)and(4c).

2.2 基于玻尔兹曼理论传输线模型的基本形式

玻尔兹曼传输方程描述了非平衡下的热动力学系统中流体特征的变化情况.从玻尔兹曼传输方程可求得沟道中一维电流密度J满足如下公式[6]:

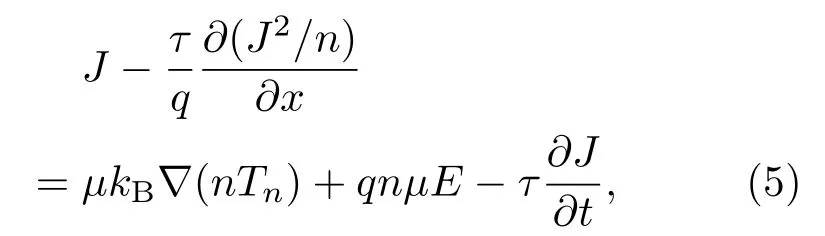
式中kB为玻尔兹曼常数,Tn为沟道内载流子温度.其中在现代模型模拟中通常省略,省略后可得到只包含亚声波流动区域的抛物线能量波矢关系曲线系统[6].同时,设定沿沟道方向的温度变化为零,给定热电压VT的定义为VT=kBTn/q,则(5)式可表达为

为进一步明确玻尔兹曼理论与经典动力学理论的差别,将(3a)式转化为电流密度形式,可得基于经典动力学理论的沟道一维电流密度为

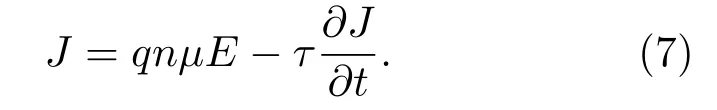
对比(6)式和(7)式,可得玻尔兹曼理论除包含经典动力学理论中的漂移部分qnµE和散射部分外,还包含扩散部分

将(7)式转换成传输线理论方程可得

结合粒子连续边界条件,可得基于玻尔兹曼理论的RCL传输线模型表达式为

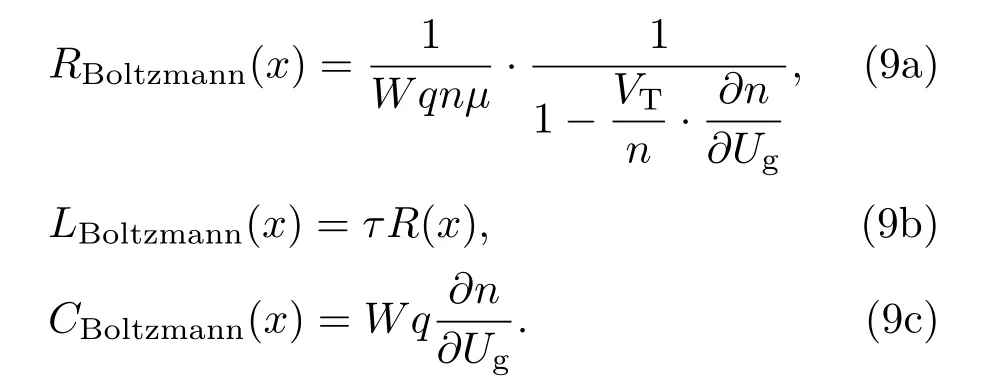
为方便对比两种模型,此处用电导取代电阻,表述RCL模型单元中载流子主要的漂移运动.由(4a)和(9a)式可得,基于流体力学德鲁德模型的总电导(每单位长度)如(10a)式,而基于玻尔兹曼传输方程的总电导(每单位长度)如(10b)式:

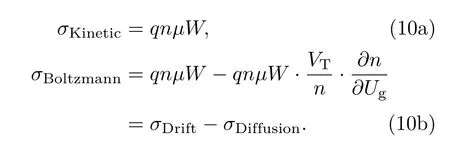
由(10b)式可得,基于玻尔兹曼理论的总电导由两部分组成,第一部分为漂移电导,其形式与流体力学德鲁德模型所得总电导相同;第二部分即为扩散电导,与温度及载流子密度随Ug的变化有关.

3 模型计算及仿真结果

为了更好地说明经典动力学传输线模型和玻尔兹曼理论传输线模型的差别,本节中根据前文理论计算,分别对两种模型进行静态下电导仿真和高频电流响应度仿真,并通过二者差值对两种模型的差异性进行阐述分析.

3.1 静态下扩散部分对整体电导的影响

根据(10a)及(10b)式,可得漂移电导和扩散电导的计算式分别为

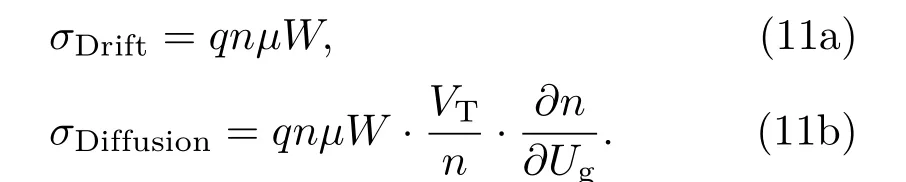
为探讨扩散电导的影响,我们用扩散电导σDiffusion与传统基于经典动力学理论总电导σKinetic的比值Raσ来表示扩散电导对整体电导的影响.Raσ的计算如(12)式所示:

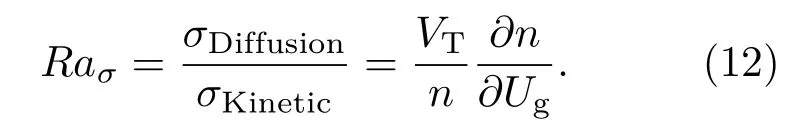
根据(12)式可计算得到扩散部分的加入对整体电导的影响.该计算中相关取值依据如下:场效应管阈值电压取为CMOS场效应管常用阈值电压Vth=0.4 V,栅极电压变化范围为CMOS场效应管常用栅极电压范围0—1 V,温度变化范围为Si材料正常工作温度273 K(0◦C)至523 K(250◦C),由此得到计算结果如图2所示.由图2(a)可知,扩散部分电导对整体电导的影响随栅极电压的增大而减小,随温度缓慢递增.这是由扩散运动本质,即粒子浓度不均匀性引起的.随着栅极电压的增大,沟道内载流子浓度随栅极电压的变化逐渐降低,粒子浓度不均匀性减小,扩散效应减弱,因此扩散电导对整体电导的影响力随之减小.当温度增大时,载流子无规则热运动增大,扩散效应随之变强.

然而在图2(a)中,温度的影响不明显.为更好地体现温度变化在扩散运动中的作用,此处取栅极电压分别为:Ugs=0.2 V,Ugs=0.4 V及Ugs=0.6 V,可得到比值Raσ在此三个栅极电压处随温度的变化如图2(b)所示.由图2(b)可知,比值Raσ随温度的增大缓慢增大,且随栅极电压的增大变化趋势逐渐减缓,这也与之前所得结论——扩散部分电导对整体电导的影响随栅极电压的增大而减小相符.

另外,一般场效应管探测器工作在室温(T=300 K),其最佳工作点在阈值电压附近(Ugs=Vth=0.4 V),由图2可以看到,此时二者之间的差值约占经典动力学模型电导的25%,仍为较大比重,故此时扩散效应不可忽略.

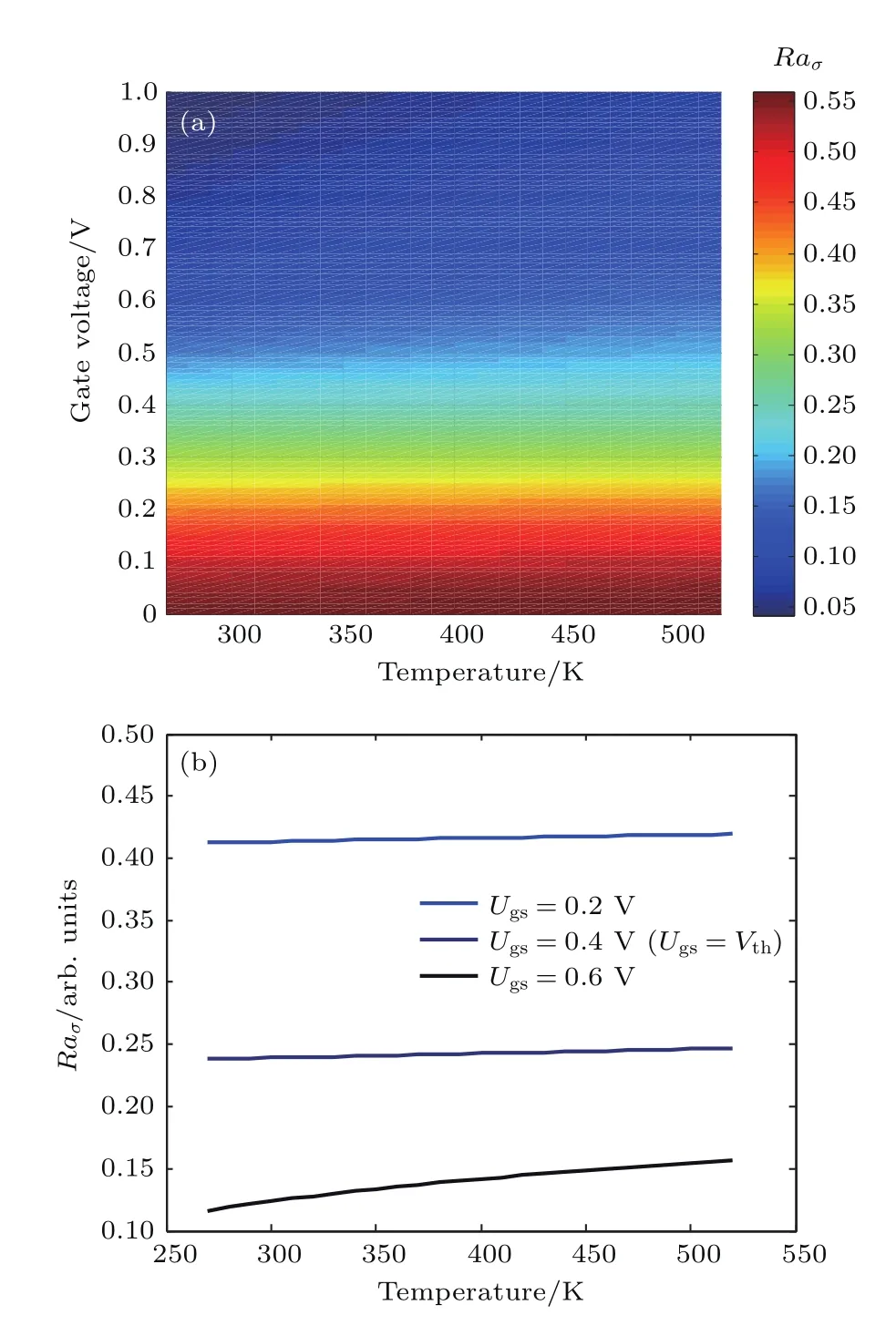
图2 (网刊彩色)(a)Raσ随栅极电压及温度的变化情况;(b)不同栅极电压下Raσ随温度的变化情况Fig.2.(color online)(a)The variation of Raσwith the gate voltage and the temperature;(b)the variation of Raσwith the temperature at di ff erent gate voltage.

3.2 扩散电导对场效应管电流响应度的影响

电流响应度是评价场效应管探测器的重要参数之一.因探测器实际工作时需配合天线完成自由空间太赫兹波耦合,故电流响应度的高低除受场效应管本身性能决定之外,还与配合天线的损耗与二者之间的匹配系数有关.此处假定天线无损耗,且天线与场效应管完全匹配,分别对基于玻尔兹曼理论模型的电流响应度ℜBoltzmann与基于经典动力学德鲁德理论模型的电流响应度ℜKinetic进行仿真分析,并为了研究二者的差别,给出其差值定义RRI为

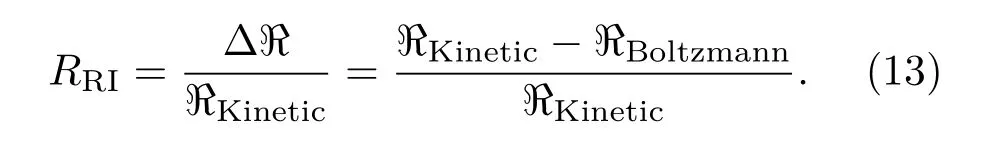
所得到的模拟计算结果如图3所示.由图3可知,二者差值随温度升高而逐渐降低,随频率增大而逐渐增大.对于CMOS场效应管探测器而言,其正常工作在室温(T=300 K)下,由图3可知,二者差值在1 THz以下差距较小,当探测器的工作频率大于1 THz时,二者的差距开始逐渐增大.

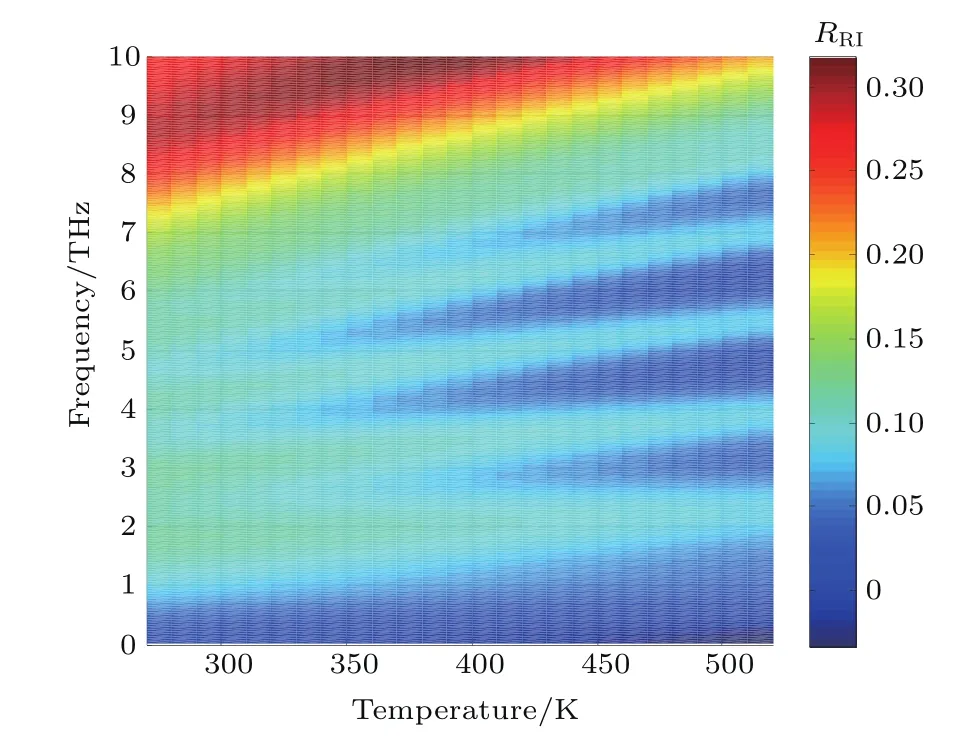
图3 (网刊彩色)RRI随栅极频率及温度的变化情况,其中,横轴为温度,纵轴为场效应管工作频率Fig.3.(color online)The variation of RRIwith the frequency and the temperature.In the fi gure,the x axis is temperature,and the y axis is the transistor working frequency.

4 仿真结果分析

由上文可知,当频率和温度不同时,RRI不同.为了给出明确的扩散部分省略条件,我们依据如下两条判断依据给出省略原则.

1)数学计算中,认为当满足

时,δ→0.

此处我们运用3σ原则对“→”运算进行判断,认为当满足

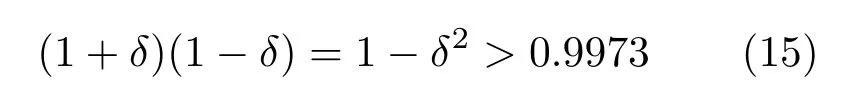
时,(1+δ)(1−δ)→1,δ→0.

2)给定命题真假评判系数α,并设定需评判的命题为模型中扩散部分可以省略.可得当扩散部分可省略成立时,命题为真,α=1;当模型中扩散部分不可省略时,命题为假,α=0.

由以上两条原则,结合(13)式与(15)式,可得当

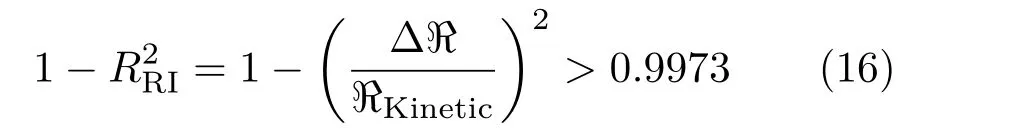
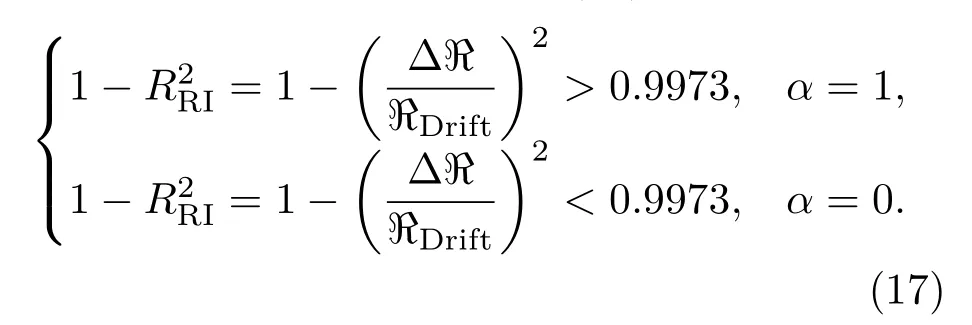
由(17)式得到α随温度及频率的变化如图4所示.其中蓝色部分为α=1,即扩散部分可省略区域;红色部分为α=0,即扩散部分不可省略区域.图4中红色占据主要部分,故可知在大部分情况下,模型中的扩散部分是不可以忽略的.只有当频率足够低(频率<1 THz)、部分频率下温度足够高时,场效应管模型可简化为只包含漂移和散射部分,忽略扩散效应对模型的影响.

图4 (网刊彩色)α随频率及温度的变化情况,图中横轴为温度,纵轴为场效应管工作频率;图中蓝色部分为扩散部分可以省略区域,红色部分为不可省略区域Fig.4.(color online)The variation of α with the frequency and the temperature.In the fi gure,the x axis is temperature,and the y axis is the transistor working frequency.The blue part is the area that the di ff usion part can be neglected in the model,and the red one is for not neglected part.

由图4可知,场效应管探测器工作频率越大,扩散效应产生的影响越明显.产生此现象的原因与沟道内载流子浓度不均匀性随频率增大而提高有关.当场效应管探测器工作在太赫兹频段并且沟道长度大于沟道内等离子体波的衰减长度时(衰减长度随等离子体波振荡频率增大而降低,太赫兹波段衰减长度一般为10—30 nm,小于常用CMOS场效应管沟道长度),太赫兹波从场效应管沟道一段耦合进沟道内,并在传输过程中等离子体波振幅迅速衰减至零.这就导致了沟道一段载流子浓度随太赫兹波振幅改变而变化,频率越高,太赫兹波振幅变化越快,载流子浓度变化越大,沟道两端的载流子浓度不均匀性也随之提高,进而令扩散效应愈发明显.因此,在高频区域,模型中的扩散运动不可忽略.

5 结 论

综上所述,本文针对现有太赫兹CMOS场效应管理论模型中忽略扩散效应的问题,通过理论计算及模拟分析给出模型中扩散部分的作用,明确了该部分可以省略的理论依据和条件.文中首先给出了基于玻尔兹曼理论的场效应管传输线模型,并将其与只包含漂移与散射效应的经典动力学理论场效应管传输线模型进行对比,从理论上得到二者之间的差别和扩散部分电导的具体表达式,并明确沟道中载流子扩散效应主要由温度及载流子密度随栅极至沟道的电压引起.其次,本文通过模拟结果给出了静态下的电导比及高频下的电流响应度之比来讨论两种模型之间的差异.结果表明:静态下,扩散部分的影响随温度的升高呈微弱增大,随栅极电压的增大而减小;常温下,当栅极电压为阈值电压时,场效应管探测器处于最佳工作点,此时扩散电导占总电导的25%;高频状态下,扩散部分对探测器电流响应度的影响随频率增大而增大,随温度升高而降低.同时,基于计算及模拟结果,我们结合3σ原则提出扩散部分可省略的具体条件:当频率足够低(频率<1 THz)或温度足够高时,模型中的扩散部分可以省略,此时两个模型可认为无差别.当场效应管工作频率高于1 THz时,模型中扩散部分的省略会导致场效应管模型的不准确.产生此现象的原因为扩散运动与沟道内载流子浓度不均匀性有关.栅极电压增大时,沟道内载流子浓度随栅极电压的变化逐渐降低,粒子浓度不均匀性减小,扩散效应减弱,因此扩散电导对整体电导的影响力随之减小;当温度增大时,载流子无规则热运动增大,扩散效应随之变强;当频率增高时,沟道一端等离子体波的振幅变化越快,而沟道另一端因衰减效应始终为零,故此时沟道两端载流子浓度变化增大,载流子浓度不均匀性变化也随之提高,进而令扩散效应愈发明显.综上所述,场效应管正常工作时的栅极电压一般在阈值电压附近,此时随着温度增高、工作频率增大,沟道内的扩散效应影响增强,在模型中不可忽略.

本文的研究工作为CMOS场效应管模型的精确建立提供了理论依据,为更好地进行场效应管的设计工作和节约成本提供了更有效的保障.

[1]Pfei ff er U R,Grzyb J,Sherry H,Cathelin A,Kaiser A 2013 38th International Conference on Infrared,Millimeter,and Terahertz Waves(IRMMW-THz)Mainz,Germany,September 1–6,2013 p1

[2]Minoru F,Shuhei A 2015 IEICE Electron.Express 12 20152006

[3]Lu J Q,Shur M S,Hesler J L 1998 Electron Dev.Lett.19 373

[4]Hadira R A,Sherry H,Grzyb J,Zhao Y 2012 IEEE J.Solid-State Circuit 47 2999

[5]Ryu M W,Lee J S,Kim K S,Park K,Yang J R,Han S T,Kim K R 2016 IEEE Trans.Electron Dev.63 1742

[6]Grasser T,Tang T,Kosina H,Selberherr S 2003 Proc.IEEE 91 251

[7]Preu S,Kim S,Verma R,Burke P G,Sherwin M S,Gossard A C 2012 J.Appl.Phys.111 024502

[8]Gutin A,Nahar S,Hella M,Shur M 2013 IEEE Trans.Terahertz Sci.Technol.3 545

[9]Ibrahim N Y,Rafat N H,Elnahwy S E A 2013 J.Infrared Millim.Terahertz Waves 34 606

[10]Tan R B,Qin H,Sun J D,Zhang X Y,Zhang B S 2013 Appl.Phys.Lett.103 173507

[11]Zhao X H,Li C,Zhang P 2013 Acta Phys.Sin.62 130506(in Chinese)[赵晓辉,蔡理,张鹏 2013物理学报62 130506]

[12]Gutin A,Ytterdal T,Muraviev A,Shur M 2015 Solid-State Electron.104 75

[13]Kim K S 2016 M.S.Thesis(Ulsan:Ulsan National Institute of Science and Technology)

[14]Liu Y,He J,Chan M S,Du C X,Ye Y,Zhao W,Wu W,Deng W L,Wang W P 2014 Chin.Phys.B 23 097102

[15]Dyakonov M I,Shur M S 1996 IEEE Trans.Electron Dev.43 1640

[16]Khmyrova I,Seijyou Y 2007 Appl.Phys.Lett.91 143515

PACS:73.43.Cd,73.50.Mx,85.30.Tv,85.60.GzDOI:10.7498/aps.66.127302

Di ff usion part in terahertz complementary metal oxide semiconductor transistor detector model∗

Zhang Jing-Shui1)Kong Ling-Qin1)Dong Li-Quan1)Liu Ming1)Zuo Jian2)Zhang Cun-Lin2)Zhao Yue-Jin1)†

1)(Institute of Opto-Electronics,Beijing Institute of Technology,Beijing 100081,China)
2)(Department of Physics,Capital Normal University,Beijing 100048,China)

1 March 2017;revised manuscript

5 April 2017)

In this paper,we discuss the di ff usion motion of carriers in the transistor channel in a terahertz frequency range,and propose an resistance-capacitance-inductance(RCL)model based on Boltzmann transport theory,and then put forward the rules to determine whether the di ff usion part in the RCL model can be neglected for terahertz fi eld-e ff ect-transistor(FET)detectors.The traditional RCL model for FET detectors is based on classic kinetic theory.In this model only the drift and the scattering motion of the carrier density in transistor channel are considered,and the di ff usion part is neglected without giving any explanation.To solve this problem,in this paper we adopt three steps: fi rst,instead of classic kinetic theory,the equations of RCL transistor model including di ff usion part are derived from Boltzmann transport equation,and by comparing the two models,the speci fi c expression for the di ff usion part is given.Second,the di ff erences between the two models are calculated and simulated,including the conductivity in quasi-static mode and the current response in high frequency mode,with di ff erent gate voltages,temperatures and working frequencies.Third,combined with the 3σ rules,the conditions to neglect the di ff usion motion in the model are put forward.The results show that the di ff usion motion of the carriers is caused by the inhomogeneity of the carrier density,a ff ected by the gate voltage,the temperature and the changing speed of the carriers with respect to the local voltage.In quasi-static mode,the role of di ff usion part will change with the gate voltage,and when the gate voltage equals threshold voltage(which is the best working point for transistor detector),the di ff usion part cannot be neglected,for which the reason is that a larger gate voltage will lead to a smaller inhomogeneity of channel carrier density and then a weaker di ff usion e ff ect,thus the e ff ect of di ff usion conductance on the whole transistor conductance becomes smaller.For the terahertz-frequency working mode,the di ff usion part will depend on temperature and frequency.With temperature increasing,the current responsivity di ff erence caused by the di ff usion part in the model slightly decreases;when the working frequency increases but below 1 THz,the di ff usion part can be neglected;however,when the working frequency is above 1 THz,the transistor model should contain drift,scattering and di ff usion part at the same time,for which the explanation is that when the temperature increases,the random thermal motion of the carrier becomes larger,thus the di ff usion e ff ect will be stronger;and if the frequency increases,the number of the carriers in one terminal of the channel will change faster,but due to the channel damping,the number of the carriers in another terminal will always be zero,thus the changing speed of the carrier density between the two terminals will be faster,then a larger inhomogeneity of carrier density and a stronger di ff usion e ff ect will appear.In conclusion,normally the transisitor works at the threshold gate voltage,and at this point,the di ff usion e ff ect in the channel will increase with working temperature and frequency increasing,thus the di ff usion part in the model cannot be neglected.The results in this paper make a signi fi cant contribution to a more accurate terahertz transistor detector model.

complementary metal oxide semiconductor transistor detector,terahertz,model simulation,Boltzmann theory

10.7498/aps.66.127302

∗国家自然科学基金(批准号:61377109)资助的课题.

†通信作者.E-mail:yjzhao@bit.edu.cn

©2017中国物理学会Chinese Physical Society

http://wulixb.iphy.ac.cn

*Project supported by the National Natural Science Foundation of China(Grant No.61377109).

†Corresponding author.E-mail:yjzhao@bit.edu.cn