硼原(离)子内壳激发高自旋态能级和辐射跃迁∗

钱新宇 孙言†刘冬冬 胡峰 樊秋波 苟秉聪

1)(徐州工程学院数学与物理科学学院,徐州 221018)

2)(北京理工大学物理学院,北京 100081)

硼原(离)子内壳激发高自旋态能级和辐射跃迁∗

钱新宇1)孙言1)†刘冬冬1)胡峰1)樊秋波1)苟秉聪2)

1)(徐州工程学院数学与物理科学学院,徐州 221018)

2)(北京理工大学物理学院,北京 100081)

(2016年11月25日收到;2017年4月18日收到修改稿)

采用Rayleigh-Ritz变分方法计算了B原子(离子)内壳层激发高自旋态(4,5,6L,L=S,P)里德伯系列的能量和精细结构劈裂,利用截断变分方法改进非相对论能量,并利用一阶微扰理论计算了相对论能量修正和质量极化效应修正,利用屏蔽的类氢公式计算了量子电动力学效应和高阶相对论效应,从而得到了高精度的组态能量.利用精确计算的波函数,计算了这些高自旋态的电偶极辐射跃迁波长、振子强度和辐射跃迁概率.通过长度规范和速度规范计算的振子强度的一致性证明了本文计算的波函数是精确的.相比其他理论计算结果,本文计算的高自旋态的能级及跃迁波长数据与实验数据符合得更好.对于一些高位的内壳层激发高自旋态,相关的能级和跃迁数据为首次报道,本文的计算结果对相关实验光谱谱线标定具有重要意义.

高自旋态,精细结构,辐射跃迁,振子强度

1 引 言

硼原子(离子)内壳层激发高自旋态位于多重离化阈之上,在狭窄的区间内具有多个能级分布,能级态密度高,电子关联效应复杂,且硼原子核外电子数相对较少,是研究原子内壳激发态的理想体系,对其内壳层激发态的研究对原子分子相关理论发展具有重要学术意义.此外,硼原子(离子)高自旋态具有较长的能级寿命,其光谱对高温等离子诊断、天体物理谱线鉴定、软X射线激光[1−3]等领域都具有较高的应用价值.对于B原子(离子)内壳层激发高自旋态,由于不能满足俄歇跃迁的自旋和角动量守恒定则,其自离化跃迁过程是禁戒的.这些高自旋态通常具有较长的寿命,在实验中能够充分积累,能够很容易地观测到其辐射跃迁光谱线.最早的测量实验是Martinson等[4]利用束箔实验技术标定了位于1701 Å,其来源的谱线来源于B2+离子四重态1s2s2p4Po—1s2p24Pe的辐射跃迁.随着束箔实验分辨率的提高,陆续报道了一些相关的实验数据.1984年,Agentoft等[5,6]和Chung等[7]测量了类锂B2+离子高自旋态2p34So和1s2lnl(4L,2L)的辐射跃迁光谱线.Baudinet-Robinet等[8,9]测量了B2+离子287—2000 Å范围内的光谱线,并标定了其中的22条谱线来自于B2+离子内壳层激发四重态,5条谱线来自于B2+离子内壳层激发二重态.1986年,Mannervik等[10]进一步测量并标定B2+离子四重态1s2s2p4Po—1s2p24Pe的跃迁光谱线位于1702.1 Å,并首次报道了1s2s3s4S—1s2s3p4Po跃迁的波长.之后,Mannervik等[11]进一步报道了B+离子五重态1s2s2p25Po—1s2p35So跃迁波长((1323.92±0.07)Å)和跃迁寿命,精确度与Martinson等[4]的实验数据精度相比大大提高.利用双激光产生等离子体技术,Jannitti等[12]和Lynam等[13]分别测量了B2+离子和B+离子内壳层激发二重态的吸收光谱线.最近,Ryabtsev等[14]和Kramida等[15,16]利用高分辨率的束箔实验技术测量了B原子(离子)的辐射跃迁光谱,并报道了50条新观测的光谱线.Fuhr和Wiese[17]综合整理并分类了B原子(离子)的辐射光谱跃迁数据,涵盖了1400多个允许跃迁和禁戒跃迁.NIST(National Institute of Standards and Technology)数据库的B2+离子内壳层激发态的相关参考数据多数来自文献[16,17].2014年,Müller等[18]利用合并光子-离子束技术测量了B+离子的K壳层光电离截面,对应的内壳层激发态包括1s2s2p23L(L=P,D),1s2p31Po,1s2s2np(n=2—4)1Po和1s2s3p23D.

理论方面,Beck和Nicolaides[19]最早使用FOTOS( fi rst-order theory of oscillator strengths)方法计算了B+离子内壳层激发五重态的组态能级和1s2s2p25P—1s2p35So跃迁概率.Chung等[7]及Gou和Deng[20]利用多组态的Rayleigh-Ritz变分方法计算了B2+离子内壳层激发四重态的能级和辐射跃迁波长,并对实验中的光谱线进行标定.利用同样的理论方法,Yang和Chung[21]及Gou和Wang[22]计算了B+离子内壳层激发五重态1s2s2pnp5Pe和1s2p2np5So的能级、精细结构和辐射跃迁数据.之后,一些理论工作者采用全实加关联(FCPC)方法[23,24]、鞍点变分方法[25]、多组态Hartree-Fock(MCHF)方法[11]、多组态Dirac-Fock方法[26]和Hylleraas方法[27]对B原子(离子)内壳层激发高自旋态能级、精细结构、辐射跃迁概率、辐射跃迁寿命等进行了计算,得到了与实验符合较好的结果.目前,虽然人们对硼原子(离子)的内壳层激发态开展了相关研究,得到了一些比较精确的理论和实验数据.然而,研究主要集中在B2+离子四重态体系.由于复杂的电子关联效应和计算过程的不稳定性,B原子(离子)内壳层激发五重态和六重态的相关理论数据还很少.由于缺乏精确的理论计算数据,也限制了相关实验的开展和实验光谱线的标定.

本文采用多组态相互作用Rayleigh-Ritz变分方法,利用截断变分方法饱和波函数空间,在考虑了相对论修正、质量极化效应、量子电动力学(QED)效应和高阶相对论效应的基础上,计算了硼原子(离子)内壳层激发高自旋态里德伯系列激发态的能级、精细结构劈裂、辐射跃迁振子强度、辐射跃迁概率、辐射跃迁波长.相比文献中的理论数据,本文的计算结果与实验符合得更好.本文的理论计算结果对相关的光谱实验研究是有意义的.

2 理论方法

在LS表象下,具有N个电子的原子体系的非相对论哈密顿算符为

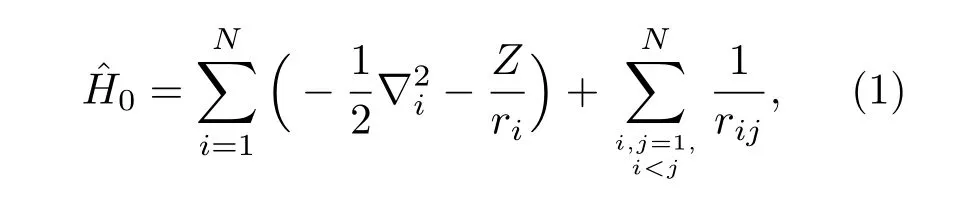
其中,ri表示第i个电子与原子核之间的距离,rij表示第i个电子和第j个电子之间的距离,Z为核电荷数.

闭通道的波函数可利用径向波函数与轨道的角动量和自旋波函数乘积作为基函数展开,波函数形式如下:

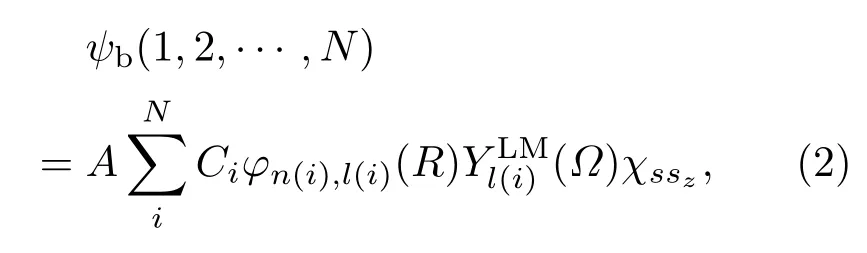
其中,A为反对称算符,Ci为线性参数,φn(i),l(i)代表径向波函数,YLMl(i)代表轨道角动量波函数,R代表径向部分,Ω代表轨道轨道角动量部分,χssz为自旋波函数.径向部分采用Slater基函数进行展开,

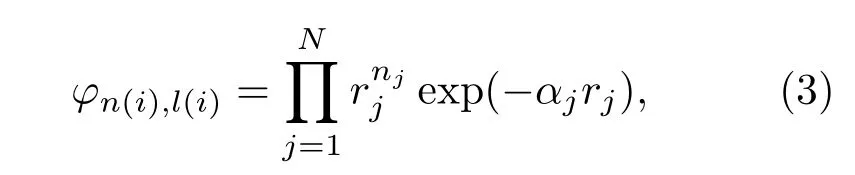
其中,αj为每个电子对应的非线性参数.

在计算中,基于Rayleigh-Ritz变分方法[28,29],利用(2)式的波函数对(1)式哈密顿算符求期望值的极小值,得到组态非相对论能量的计算公式如下:

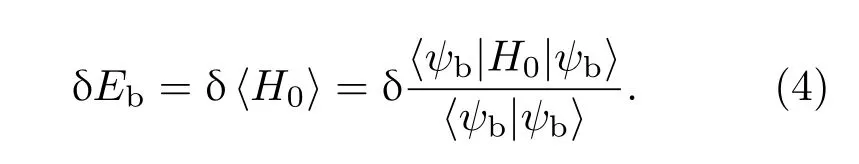
在(4)式中,利用Rayleigh-Ritz变分对非线性参数集{αj}及线性参数Ci优化能量极小,从而得到组态的非相对论能量Eb.

为了进一步饱和束缚空间,获得高精度的非相对论能量,本文采用截断变分[18]方法对非相对论能量进行修正.经过截断变分修正后得到的总波函数为

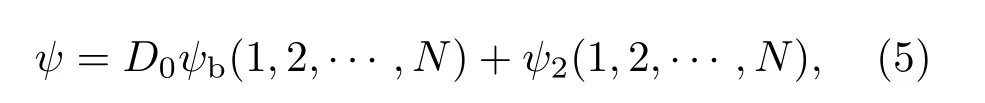
其中,

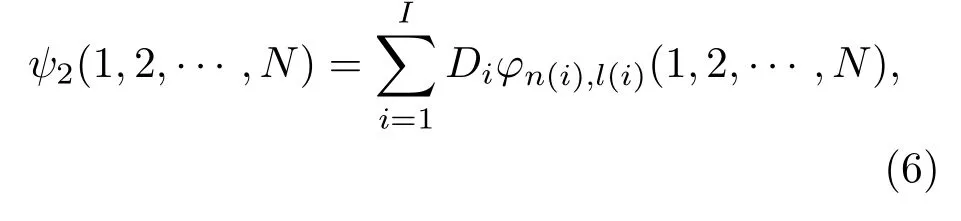
其中,D0,Di为线性参数;I为所添加的进行截断变分的角动量-自旋分波数目.在截断变分的计算过程中,ψb的非线性参数保持不变,对ψ2中的每个非线性参数进行优化.

为了进一步获得更高精度的能量,还需要考虑相对论修正和质量极化效应的影响.在本文中,利用一阶微扰理论对相对论修正和质量极化效应进行计算.质量极化算符为Hmp.相对论修正算符包括动能修正项Hk、达尔文项HD、电子和电子相互作用项Hee以及轨道和轨道相互作用项Hoo.这些算符在文献[30]中有详细描述,这里不再赘述.

于是,相对论能量修正为

质量极化修正为

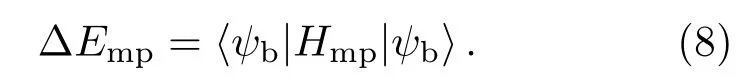
利用屏蔽的类氢公式[31],本文还考虑QED效应和高阶相对论效应对组态能量的修正∆EQ+H.对于QED效应和高阶相对论效应的修正在文献[32]中有详细讨论,这里不再展开.

通过对非相对论能量、截断变分能量、相对论修正、质量极化效应、QED和高阶相对论效应修正求和,得到组态总能量为

在Pauli-Breit相对论近似下,精细结构的能量微扰算符为[33]

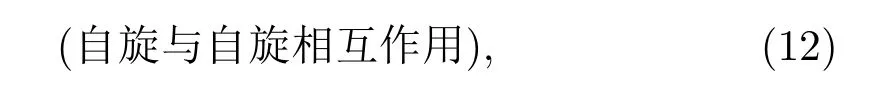
式中li,si分别为第i个电子的轨道和自旋角动量;pi为第i个电子的动量;c为光速.

3 结果与讨论

本文采用多组态Rayleigh-Ritz变分方法计算了硼原子(离子)内壳层激发高自旋态的能级和精细结构劈裂.硼原子(离子)内壳高位激发态是一个复杂的多电子系统,电子关联效应十分复杂,要获得精确的理论计算数据,如何选取高精度的波函数是关键.本文计算中采用多组态相互作用的基函数来考虑电子关联效应,其中每个基函数采用Slater型径向波函数与轨道角动量和自旋角动量波函数的乘积构成.轨道角动量和自旋角动量关联效应通过在试探波函数里添加适当的轨道角动量和自旋角动量分波来考虑.描述电子径向波函数的Slater型函数的非线性参数在变分过程中通过优化能量极小获得.为了保证重要的角动量-自旋分波不被遗漏,并且能够充分考虑组态相互作用,本文根据能量相近、宇称相同、具有相同的L和S量子数的组态相互作用定则来选取轨道-自旋角动量组态分波.例如,对于1s2s3s4S内壳层激发四重态,重要的轨道角动量分波[l1,l2,l3]为[0,l,l](l=1—7),[1,l,l+1](l=1—3),[2,2,2],[2,2,4]等. 每个分波电子主量子数n的大小根据增大n所引起的总能量变化来确定,当增大n时,若对总能量的贡献小于1×10−7a.u.则停止增加,从而保证重要的轨道-自旋角动量组态分波的组态相互作用能够被充分考虑.表1列出了本文计算的B原子(离子)各内壳层激发高自旋态重要的角动量系列分波.高自旋态的自旋角动量波函数,只有一种耦合方式,而轨道角动量的耦合方式则有多种,在计算过程中,需要考虑到每一种可能的耦合方式,将轨道角动量波函数和自旋波函数相乘组成各分波的轨道-自旋角动量波函数.为了尽可能的提高精确度,波函数构建时选取大的基函数,对于某些组态,轨道-自旋角动量组态分波的数目达到78,其Slater基函数的数目超过2500项.在表1中,l的取值范围为0到7,l>7时的组态分波对总能量贡献很小,利用截断变分方法进行计算.构建的试探波函数经过变分优化,从而得到最佳的波函数和对应的非相对论能量Eb.

表1 B原子(离子)高自旋态波函数重要的轨道角动量分波Table 1.The important orbital angular momentum partial wave for the high-spin state of B atomic(ion).

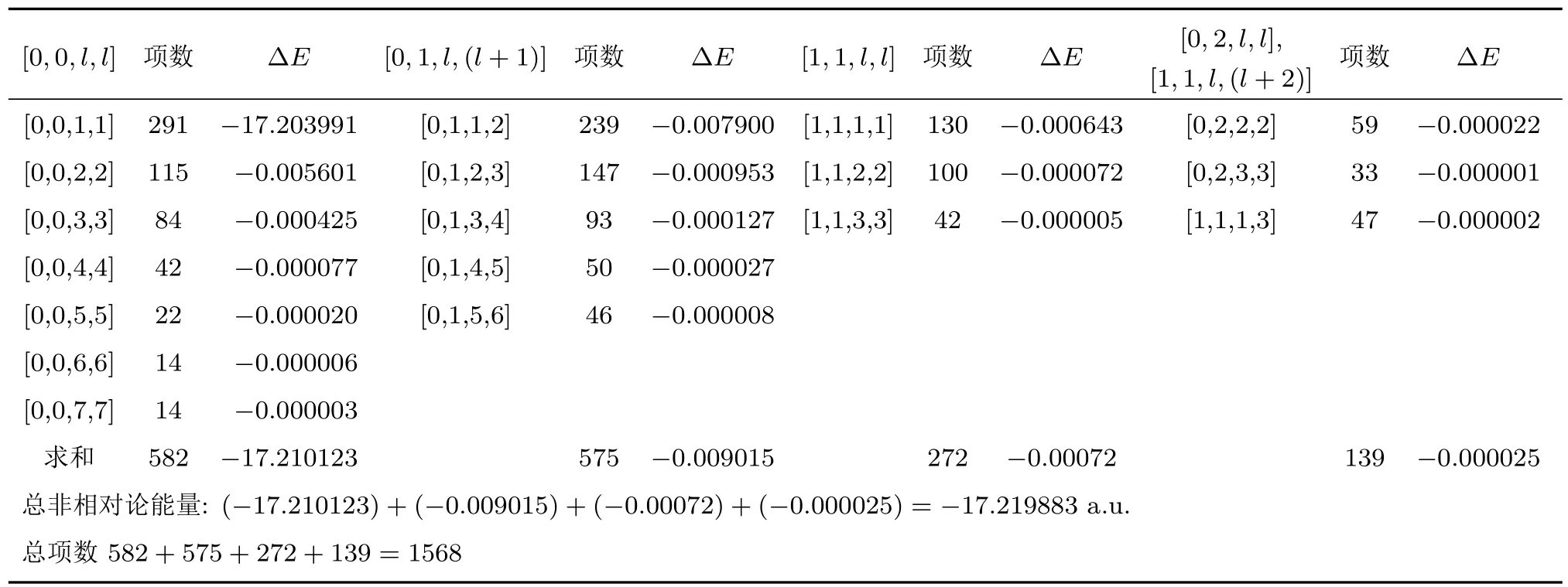
表2 B+离子五重态1s2s2p25Pe的非相对论能量计算值及各轨道角动量分波的能量贡献∆E(单位a.u.)Table 2.The non-relativistic energy and the energy contributions of each angular momentum partial wave for the quintuplet state 1s2s2p25Pein B+ion(unit a.u.).

为了验证计算的能量收敛性,表2列出了B+离子激发态1s2s2p25Pe非相对论能量计算过程中所添加的轨道角动量分波、各分波项数及各分波的能量贡献.从表2可以看出,随着电子轨道角动量l的增加,轨道角动量分波的能量贡献越来越小,计算的非相对论能量呈现收敛趋势.如表2中所列的[0,0,l,l]系列,[0,0,1,1]分波的能量贡献为−17.203991 a.u.,[0,0,7,7]分波的能量贡献仅为−0.000003 a.u..通过收敛性判断,可以保证所有重要的轨道-自旋角动量组态分波均被加入到波函数中.在计算过程中,为了饱和波函数空间,考虑高l的分波对能量的贡献,利用截断变分方法来计算非相对能量改进∆ERV,本文计算的∆ERV值约为100µa.u..利用一阶微扰理论,计算组态的质量极化修正能量∆Emp和相对论修正能量∆Erel.进一步利用屏蔽的类氢公式计算各组态的QED和高阶相对论修正∆EQ+H,最后求和得到组态的相对论能量.

表3列出了本文计算的B原子(离子)高自旋态1s2lnl(l=s,p)4Se,2p2np4So;1s2s2pnp5Se,1s2p2np5So;1s2s2p3snp6Se,1s2s2p2np6So的能量.表4列出了B原子(离子)高自旋态1s2pnp4Pe,1s2snp4Po;1s2s2pnp5Pe,1s2s2pnl(l=s,d)5Po;1s2s2p2nl(l=s,d)6Pe,1s2s2p2np6Po的能量及精细结构劈裂.表3和表4中还列出了高分辨率束箔碰撞实验[16]的数据、Rayleigh-Ritz变分方法[5,7,21,22]、FCPC[23]方法、MCHF方法[11]的理论计算值.为了便于比较,图1给出了B原子(离子)内壳层激发高自旋态能量的理论计算值与实验值[16]的偏差.从图1可以看出,本文的理论计算值与实验值的平均偏差约为6×10−4a.u.,小于文献中Rayleigh-Ritz[5,7,21,22]和FCPC[23]方法与实验的偏差.这主要是因为相比文献中的理论方法,本文计算过程中考虑了QED效应和高阶相对论效应修正∆EQ+H.本文计算的B原子(离子)的内壳层激发高自旋态,∆EQ+H主要来自于1s和2s电子.对于本文计算的1s2snl系列激发态,∆EQ+H大小约为500µa.u.;对于2p2np系列激发态,∆EQ+H很小,约为20µa.u..总体上看,FCPC方法[23]的理论计算值要略差于Rayleigh-Ritz变分方法[5,7,21,22]的理论计算值,这主要是由于FCPC方法没有充分考虑原子实内电子和原子实外电子的关联效应.这里需要指出的是,在图1中,本文没有给出高自旋态2p34So能量的理论计算值和实验值的对比.对于高自旋态2p34So,本文的理论计算值为−7.12042 a.u.,比文献[16]的实验数据−7.11158 a.u.低0.00884 a.u..在文献[16]中,该高自旋态的实验测量误差为1500 cm−1(约为0.00683 a.u.),实验误差较大.本文计算的2p34So能量的略超出实验误差约0.002 a.u..然而,本文的理论计算值与文献[5]的理论计算值−7.12023 a.u.符合得非常好.对于该激发态,目前还尚未有其他的实验数据可对比,因此还需要进一步的实验去验证.在表3和表4中,本文的计算数据比Mannervik等[11]利用MCHF的计算数据略低,这主要是由于本文采用了更大的基函数,考虑了更多的组态相互作用.

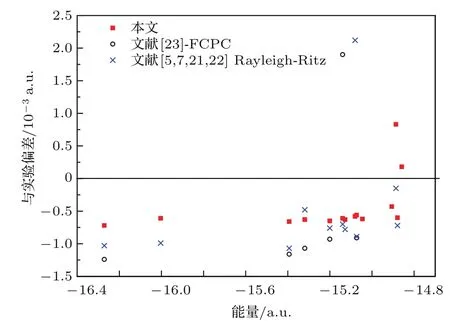
图1 (网刊彩色)B原子(离子)内壳层激发高自旋态能量理论值与实验数据[16]的偏差Fig.1. (color online)The deviation of theoretical and experimental energy data[16]for the core-excited states of B atomic(ion).

表3B原子(离子)高自旋态1s2lnl(l=s,p)4Se,2p2np4So;1s2s2pnp5Se,1s2p2np5So;1s2s2p3snp6Se,1s2s2p2np6So的能量(单位a.u.)Table 3.Energies(a.u.)of high-spin states 1s2lnl(l=s,p)4Se,2p2np4So;1s2s2pnp5Se,1s2p2np5So;1s2s2p3snp6Se,1s2s2p2np6Soof B atomic(ion).

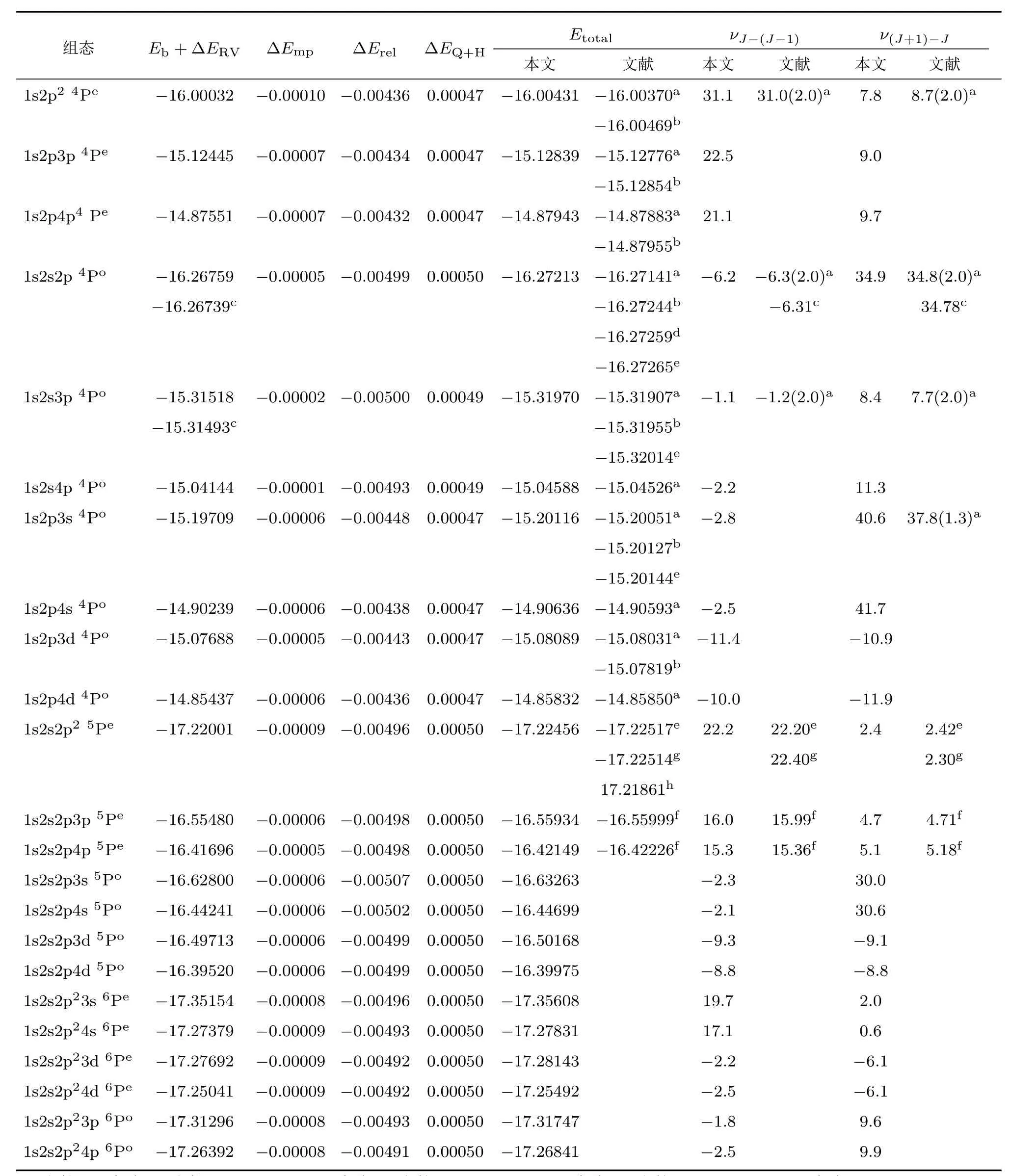
表4 B原子(离子)高自旋态1s2pnp4Pe,1s2snp4Po;1s2s2pnp5Pe,1s2s2pnl(l=s,d)5Po;1s2s2p2nl(l=s,d)6Pe,1s2s2p2np6Po的能量(单位a.u.)及精细结构劈裂(单位cm−1),其中,νJ−(J−1)和ν(J+1)−J为对应组态的精细结构劈裂值(单位cm−1),B2+离子四重态J=1.5,B+离子五重态J=2,B原子六重态J=2.5,括号中的数代表实验误差(单位cm−1)Table 4.Energies(a.u.)and fi ne structure splittings(cm−1)of high-spin states 1s2pnp4Pe,1s2snp4Po;1s2s2pnp5Pe,1s2s2pnl(l=s,d)5Po;1s2s2p2nl(l=s,d)6Pe,1s2s2p2np6Poof B atomic(ion). νJ−(J−1)and ν(J+1)−Jare the corresponding fi ne structure splitting values.For the quartet state,the quintuplet state,and the sextet state,J values are equal to 1.5,2,and 2.5,respectivley.The data in parentheses represents the experimental errors(unit cm−1).

考虑自旋与轨道、自旋与其他轨道和自旋与自旋的相互作用,表4还列出了B原子(离子)高自旋里德伯系列激发态2S+1PJ(S=1.5,2.0,2.5)的精细结构劈裂.对比的参考文献数据主要来自于束箔实验[16]、Rayleigh-Ritz变分的理论计算值[20−22,24,33]和FCPC的理论计算值[24].通过对比发现,除1s2p3s4Po高自旋态的ν2.5−1.5的精细结构劈裂值40.6 cm−1略超出实验的误差范围(37.8±1.3)cm−1,其余的计算值均在误差范围之内.本文计算的精细结构劈裂数据与文献[21,22,24]的理论计算值符合得很好,最大偏差约4%.分析表4中精细结构劈裂值,可以发现1s2pnd4Po,1s2s2pnd5Po,1s2s2p2nd6Pe(组态结构分别为spd,sspd,ssppd)的精细结构劈裂值均为负,1s2pnp4Pe,1s2s2pnp5Pe,1s2s2p2ns6Pe(组态结构分别为spp,sspp,ssspp)的精细结构劈裂值均为正.对于里德伯系列激发态一般具有均匀变化的精细结构劈裂值,因此,通过精细结构劈裂的变化能够验证里德伯系列激发态标定的组态结构.

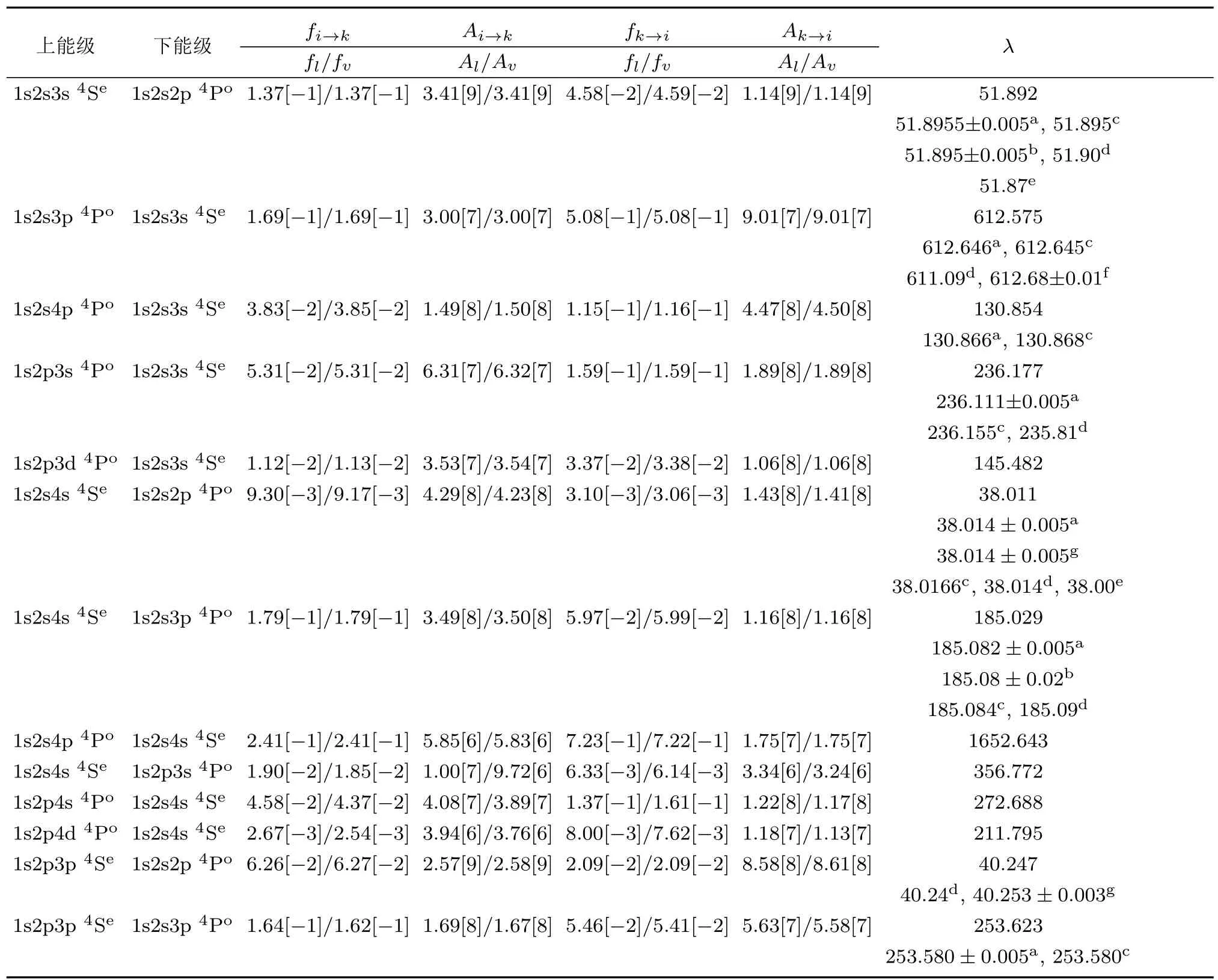
表 5 B2+离子四重态1s2sns4Se—1s2sn′p4Po,1s2sns4Se—1s2pn′l4Po,1s2pnp4Se—1s2sn′p4Po,2p2np4So—1s2pn′p4Pe;B+离子五重态1s2s2pnp5Se—1s2s2pn′l5Po,1s2p2np5So—1s2s2pn′p5Pe;B原子六重态1s2s2p3snp6Se—1s2s2p2n′p6Po,1s2s2p3p3d6Se—1s2s2p2n′p6Po,1s2s2p2np6So—1s2s2p2n′l6Pe(n 6 4;n′6 4;l=s,d)的辐射跃迁振子强度fi→k、辐射跃迁概率Ai→k(s−1)、吸收振子强度fk→i、吸收跃迁概率Ak→i(s−1)和跃迁波长λ(nm);方括号中的数代表10的幂指数Table 5.The radiative transition oscillator strength fi→k,radiative transition rate Ai→k(s−1),absorb oscillator strength fk→i,absorption transition rate Ak→i(s−1),and transition wavelength λ (nm)of the 1s2sns4Se–1s2sn′p4Po,1s2sns4Se–1s2pn′l4Po,1s2pnp4Se–1s2sn′p4Po,2p2np4So–1s2pn′p4Petransitions in B2+ion;the 1s2s2pnp5Se–1s2s2pn′l5Po,1s2p2np5So–1s2s2pn′p5Petransitions in B+ion,and the 1s2s2p3snp6Se–1s2s2p2n′p6Po,1s2s2p3p3d6Se–1s2s2p2n′p6Po,1s2s2p2np6So–1s2s2p2n′l6Pe(n 6 4;n′6 4;l=s,d)transitions in B atom.The number in square brackets represents the power of 10.

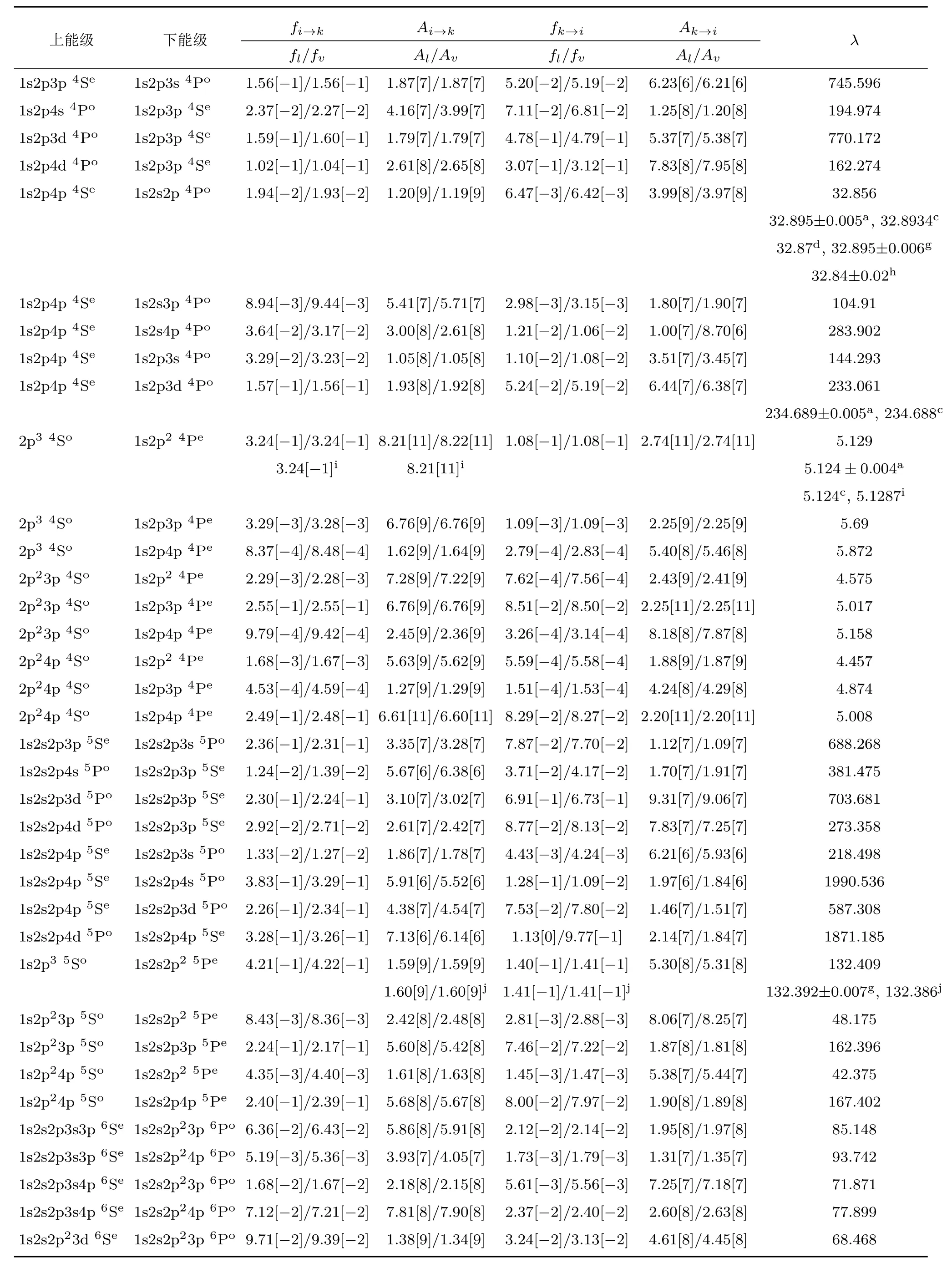
表5 (续)

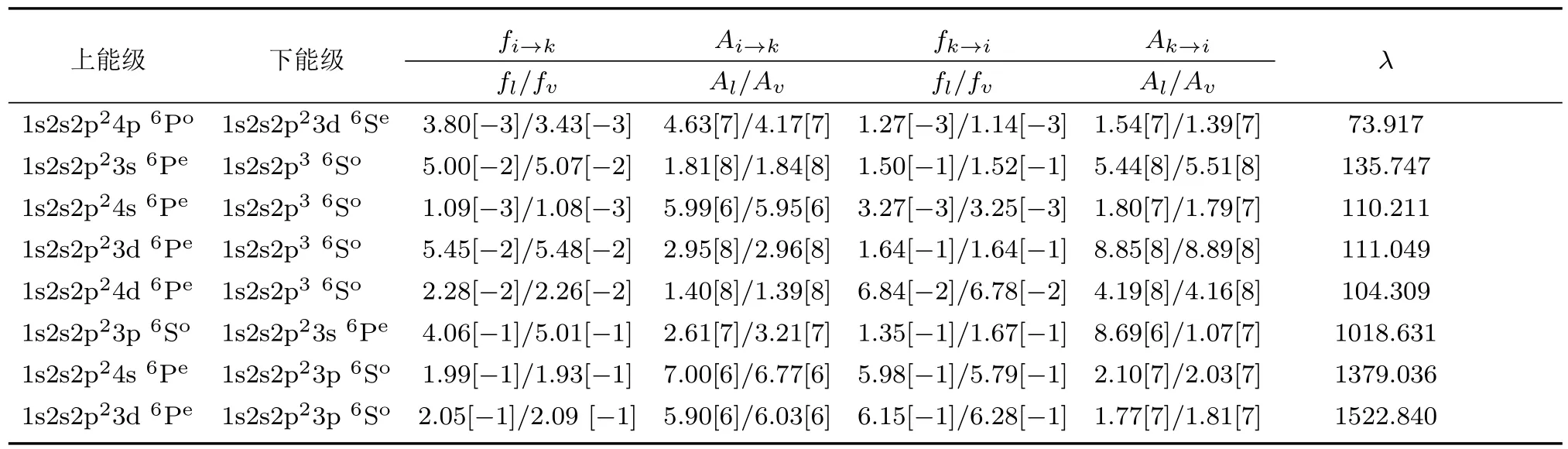
表5 (续)

表5列出了硼原子(离子)内壳层激发高自旋态1s2sns4Se—1s2sn′p4Po,1s2sns4Se—1s2pn′l4Po,1s2pnp4Se— 1s2sn′p4Po,2p2np4So— 1s2pn′p4Pe;1s2s2pnp5Se— 1s2s2pn′l5Po,1s2p2np5So— 1s2s2pn′p5Pe;1s2s2p3snp6Se—1s2s2p2n′p6Po,1s2s2p3p3d6Se— 1s2s2p2n′p6Po,1s2s2p2np6So— 1s2s2p2n′l6Pe(n 6 4;n′6 4;l=s,d)的电偶辐射跃迁振子强度、辐射跃迁概率、吸收振子强度、吸收跃迁概率和跃迁波长.表6列出了硼原子(离子)内壳层激发高自旋态1s2pnp4Pe— 1s2sn′p4Po,1s2pnp4Pe— 1s2pn′l4Po;1s2s2pnp5Pe— 1s2s2pn′l5Po;1s2s2p2nl6Pe—1s2s2p2n′p6Po(n 6 4;n′6 4;l=s,d)的电偶极辐射跃迁振子强度、辐射跃迁概率和跃迁波长.在表5和表6中,本文给出了利用长度规范和速度规范计算的跃迁振子强度和跃迁概率.根据两种规范计算结果的一致性程度,可判断计算的波函数的精确程度.为了便于比较两种规范计算结果的一致性,图2给出了硼原子(离子)高自旋态电偶极辐射跃迁振子强度的两种规范fl和fv的对比情况.从图2可以看出,两者比值的对数取值(log10(fl/fv))均位于[−0.1,0.1]范围.在振子强度fl小于0.3的范围,两种规范符合得非常好,大多数位于[−0.05,0.05]范围.在fl大于0.3的范围,两种规范一致性略差.总体上,本文计算的辐射跃迁振子强度的两种规范的计算结果显示出良好的一致性,从而证明了计算的波函数是比较精确的.表5和表6还列出了文献[5,7,22]计算的B离子高自旋态电偶极辐射跃迁振子强度和跃迁概率,本文的计算结果和文献[5,7,22]的理论计算结果符合得很好.如对于B2+离子高自旋态2p34So—1s2p24Pe的跃迁,本文的计算振子强度和跃迁概率值分别为0.324和8.21×1011s−1,和文献[5]的理论值完全一致.表5和表6的最后一列给出了本文计算的B原子(离子)高自旋态电偶极辐射跃迁波长和相关实验数据[6,8−10,16]及其他理论计算值[5,7,16,22,27].图3给出了本文计算的B原子(离子)高自旋态辐射跃迁波长和实验数据[6,8−10,16]的相对偏差.从图3可以看出,1s2p4p4Se—1s2p3d4Po和1s2p4d4Po—1s2p3p4Pe两个跃迁波长值与实验的相对偏差较大(约为0.7%和0.3%),其余跃迁波长的相对偏差均小于0.15%.对比本文计算的波长与其他理论计算值[5,7,16,22,27],相对偏差均小于0.7%.因此,整体上本文计算的B原子(离子)高自旋态电偶极辐射跃迁的波长与实验和其他理论结果符合得较好.对于B原子(离子)内壳层激发五重态和六重态,尤其是高n的里德伯系列激发态,相关的实验和理论的辐射跃迁数据还很少,需要进一步研究.本文的理论计算结果可为将来的实验和光谱谱线标定提供有价值的理论参考数据.

图2 本文计算的B原子(离子)电偶极跃迁的振子强度的长度规范fl和速度规范fv的比较Fig.2. Comparison of the calculated oscillator strengths in length gauge fland velocity gauge fvin this work.

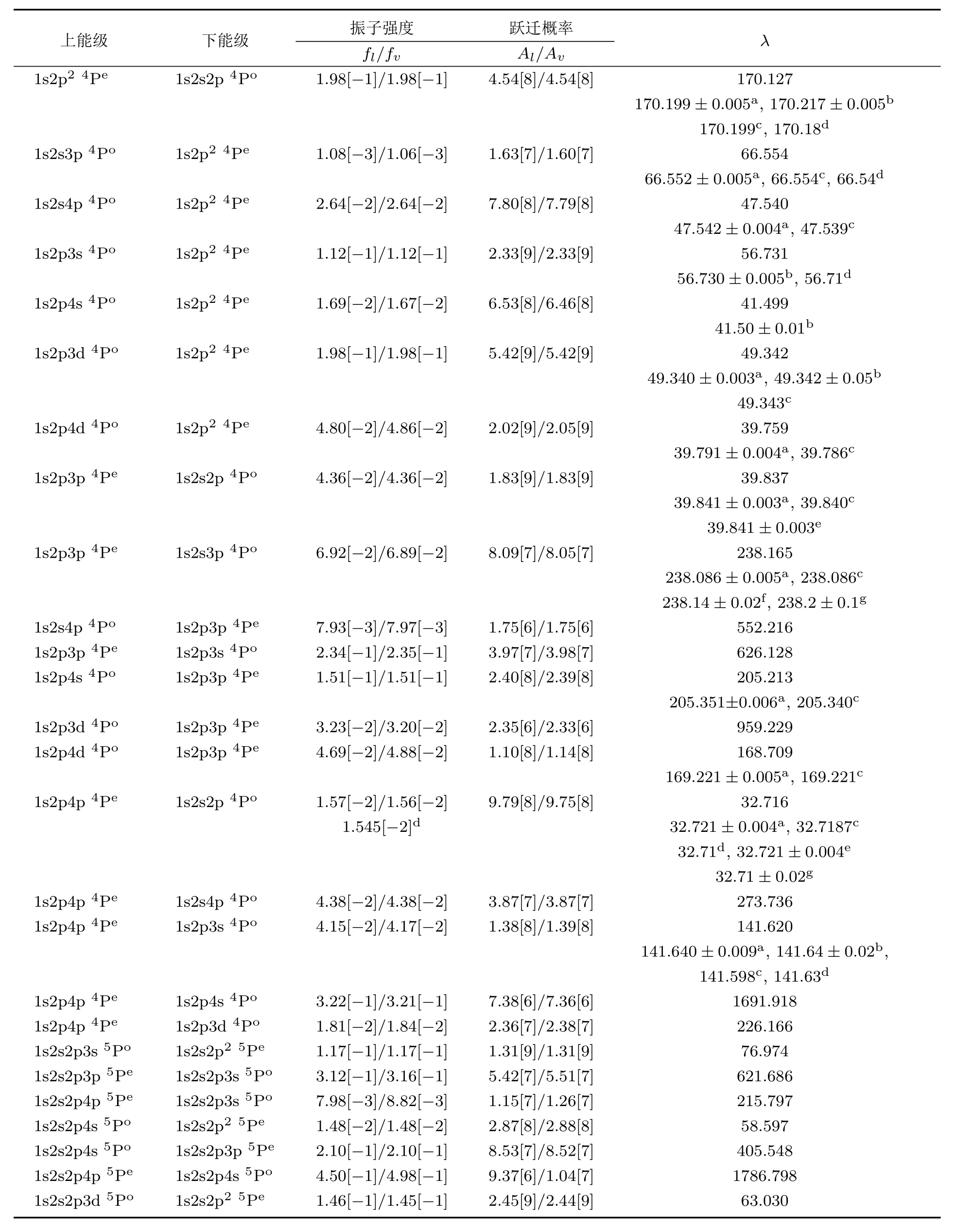
表6 B2+离子四重态1s2pnp4Pe—1s2sn′p4Po,1s2pnp4Pe—1s2pn′l4Po;B+离子五重态1s2s2pnp5Pe—1s2s2pn′l5Po;B原子六重态1s2s2p2nl6Pe—1s2s2p2n′p6Po(n 6 4;n′6 4;l=s,d)的电偶极跃迁振子强度fl/fv,跃迁概率Al/Av(s−1)和跃迁波长λ(nm);方括号中的数代表10的幂指数Table 6.The electric dipole transition oscillator strength fl/fv,transition rate Al/Av(s−1),and transition wavelength λ(nm)of the 1s2pnp4Pe–1s2sn′p4Po,1s2pnp4Pe–1s2pn′l4Potransitions in B2+ion,the 1s2s2pnp5Pe–1s2s2pn′l5Potransitions in B+ion,and the 1s2s2p2nl6Pe–1s2s2p2n′p6Potransitions in B atom(n 6 4;n′6 4;l=s,d).The number in square brackets represents the power of 10.

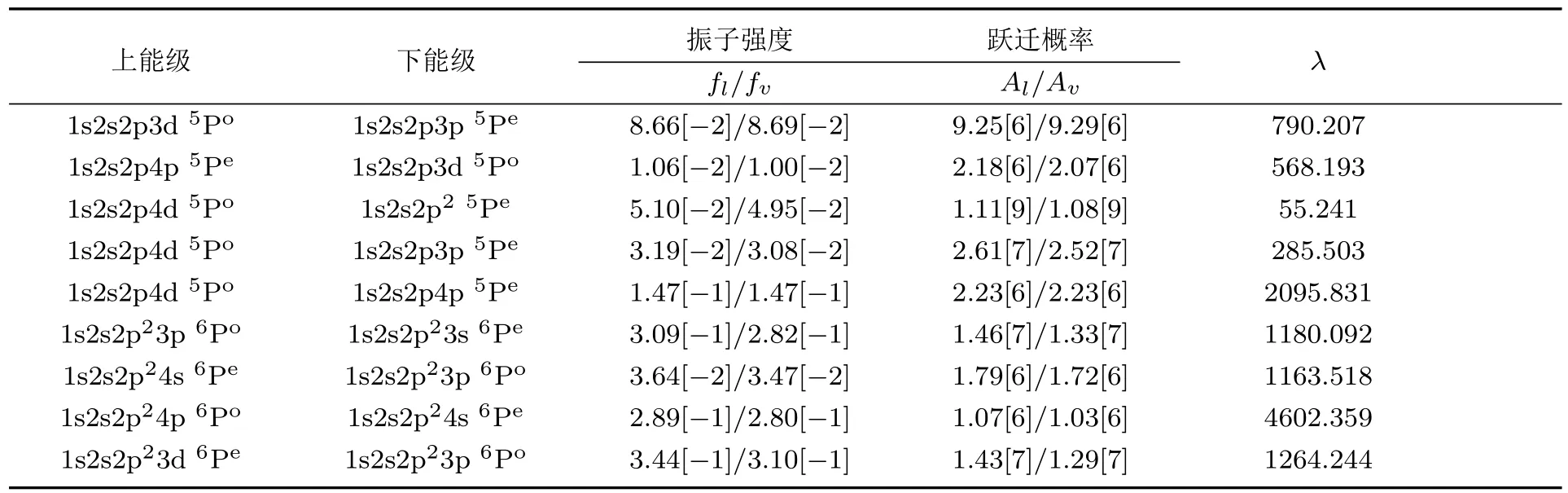
表6 (续)

图3 (网刊彩色)本文的计算B离子内壳层激发高自旋态电偶极跃迁波长和实验数据[6,8−10,16]对比的相对偏差Fig.3.(color online)Relative deviation of the calculated electric dipole transition wavelength and the experimental data[6,8−10,16]for the core-excited highspin states of B ion.

4 结 论

本文采用多组态相互作用Rayleigh-Ritz变分方法,计算了B原子(离子)内壳层激发高自旋态里德伯系列的非相对论能量和精细结构劈裂,并利用截断变分方法计算了高l系列分波的非相对论能量修正.考虑了相对论修正、质量极化效应、QED效应和高阶相对论效应,得到了精确的相对论能量.利用精确计算的波函数,对B原子(离子)高自旋态系列电偶极辐射跃迁振子强度、跃迁概率、跃迁波长展开计算.跃迁振子强度的长度规范和速度规范结果总体上显示出良好的一致性,从而证明本文计算的波函数是比较精确的.相比文献中的理论数据,本文计算的B原子(离子)内壳层激发高自旋态的能级和辐射跃迁数据与实验数据符合得更好.对于一些B原子和B+离子的高自旋激发态,相关的能级和跃迁数据为首次报道.本文的理论计算结果可为相关的实验光谱线的标定提供有价值的理论参考数据.

[1]Johansson S G,Litzén U,Kasten J,Kock M 1993 Astrophys.J.403 L25

[2]Lin B,Berry H G,Shibata T,Livingston A E,Garnir H,Bastin T,Désesquelles J 2004 J.Phys.B:At.Mol.Opt.Phys.37 2797

[3]Gu M F,Beiersdorfer P,Lepson J K 2011 Astrophys.J.732 91

[4]Martinson I,Bickel W S,Olrne A 1970 J.Opt.Soc.Am.60 1213

[5]Agentoft M,Andersen T,Chung K T 1984 J.Phys.B:At.Mol.Opt.Phys.17 L433

[6]Agentoft M,Andersen T,Chung K T,Davis B F 1985 Phys.Scr.31 74

[7]Chung K T,Bruch R,Träbert E,Heckmann P H 1984 Phys.Scr.29 108

[8]Baudinet-Robinet Y,Garnir H P,Dumont P D 1986 Phys.Rev.A 34 4722

[9]Baudinet-Robinet Y,Dumont P D,Garnir H P,Träbert E,Heckmann P 1987 Z.Phys.D:Atoms,Molecules and Clusters 7 47

[10]Mannervik S,Cederquist H,Martinson I 1986 Phys.Rev.A 34 231

[11]Mannervik S,Cederquist H,Martinson I,Brage T,Fischer C F 1987 Phys.Rev.A 35 3136

[12]Jannitti E,Nicolosi P,Tondello G 1984 Physica C 124 139

[13]Lynam W G,Carroll P K,Costello J T,Evans D,O’Sullivant G 1992 J.Phys.B:At.Mol.Opt.Phys.25 3963

[14]Ryabtsev A N,Kink I,Awaya Y,Ekberg J O,Mannervik S,Ölme A,Martinson I 2005 Phys.Scr.71 489

[15]Kramida A E,Ryabtsev A N 2007 Phys.Scr.76 544

[16]Kramida A E,Ryabtsev A N,Ekberg J O,Kink I,Mannervik S,Martinson I 2008 Phys.Scr.78 025301

[17]Fuhr J R,Wiese W L 2010 J.Phys.Chem.Ref.Data 39 013101

[18]Müller A,Schippers S,Phaneuf R A,Scully S W J,Aguilar A,Cisneros C,Gharaibeh M F,Schlachter A S,McLaughlin B M 2014 J.Phys.B:At.Mol.Opt.Phys.47 135201

[19]Beck D R,Nicolaides C A 1977 Phys.Lett.A 61 227

[20]Gou B C,Deng W S 2000 Phys.Rev.A 62 032705

[21]Yang H Y,Chung K T 1995 Phys.Rev.A 51 3621

[22]Gou B C,Wang F 2004 Phys.Rev.A 69 042513

[23]Qu L H,Wang Z W,Li B W 1998 J.Phys.B:At.Mol.Opt.Phys.31 2469

[24]Qu L H,Wang Z W,Li B W 1998 Chin.Phys.Lett.15 329

[25]Sun Y,Liu D D,Mei M F,Zhang C M,Han C,Hu F,Gou B C 2015 J.Quant.Spectrosc.Radiat.Transfer 167 145

[26]Brooks R L,Hardis J E,Berry H G,Curtis L J,Cheng K T,Ray W 1980 Phys.Rev.Lett.45 1318

[27]Larsson S,Crossley R 1982 Int.J.Quantum Chem.22 837

[28]Ritz W,Reine J 1908 Agnew.Math.35 1

[29]Chung K T 1979 Phys.Rev.A 20 1743

[30]Davis B F,Chung K T 1984 Phys.Rev.A 29 1878

[31]Drake G W F 1982 Adv.Mol.Phys.18 399

[32]Lin B,Berry H G,Shibata T,Livingston A E,Garnir H P,Bastin T,Désequelles J,Savukov I 2003 Phys.Rev.A 67 062507

[33]Sun Y,Gou B C,Zhu J J 2010 Acta Phys.Sin.59 3878(in Chinese)[孙言,苟秉聪,朱婧晶 2010物理学报 59 3878]

[34]Chung K T,Bruch R 1983 Phys.Rev.A 28 1418

PACS:31.15.A–,31.15.ac,31.10.+z,32.30.–rDOI:10.7498/aps.66.123101

Energy levels and radiative transitions of the core-excited high-spin states in boron atom(ion)∗

Qian Xin-Yu1)Sun Yan1)†Liu Dong-Dong1)Hu Feng1)Fan Qiu-Bo1)Gou Bing-Cong2)

1)(School of Mathematic and Physical Science,Xuzhou University of Technology,Xuzhou 221018,China)
2)(School of Physics,Beijing Institute of Technology,Beijing 100081,China)

25 November 2016;revised manuscript

18 April 2017)

Energy levels of the core-excited high-spin Rydberg states(4,5,6L,L=S,P)in boron atom(ion)are calculated by the Rayleigh-Ritz variation method with using large-scale multi-con fi guration wave functions.The important orbital-spin angular momentum partial waves are selected based on the rule of con fi guration interaction.The computational convergence is discussed by the example of the contribution from each partial wave in the non-relativistic energy calculations of the high-spin state 1s2s2p25Pein B+ion.To saturate the wave functional space and improve the non-relativistic energy,the restricted variational method is used to calculate the restricted variational energy.Furthermore,the mass polarization e ff ect and relativistic energy correction are included by using a fi rst-order perturbation theory.The quantum electrodynamic e ff ects and higher-order relativistic contributions to the energy levels are also calculated by the screened hydrogenic formula.Then,the accurate relativistic energy levels of these high-spin states of B atom(ion)are obtained by adding the non-relativistic energy and all corrections.The fi ne structure splitting of these high-spin states is also calculated by the Breit-Pauli operators in the fi rst-order perturbation theory.Compared with other theoretical results,our calculation results are in good accordance with the experimental data.

The absorption oscillator strengths,emission oscillator strengths,absorption rates,emission rates,and transition wavelengths of the electric-dipole transitions between these high-spin states of B atom(ions)are systematically calculated by using the optimized wave functions.The oscillator strengths and transition rates are obtained in both the length and velocity gauges.By comparing the two gauge results of oscillator strength,we fi nd that there is a good consistency between them when fl<0.3,and a reasonable consistency is obtained when fl>0.3.The accordance between the length and the velocity gauge results re fl ects that the calculated wave functions in this work are reasonably accurate.The calculated transition data are also compared with the corresponding experimental and other theoretical data.Good agreement is obtained except the wavelengths for two transitions:1s2p4p4Se–1s2p3d4Poand 1s2p4d4Po–1s2p3p4Pe.The relative di ff erences between our theoretical results and experimental data are 0.7%and 0.3%,respectively.They need to be veri fi ed by further theoretical and experimental studies.For some core-excited high-spin states,the related energy levels and transition data are reported for the fi rst time.Our calculation results will provide valuable data for calculating the spectral lines in the relevant experiments.

high-spin state, fi ne structure splitting,radiative transition,oscillator strength

10.7498/aps.66.123101

∗国家自然科学青年基金(批准号:11604284)和国家自然科学基金(批准号:11474020)资助的课题.

†通信作者.E-mail:suenyangu@163.com

©2017中国物理学会Chinese Physical Society

http://wulixb.iphy.ac.cn

*Project supported by the Young Scientists Fund of the National Natural Science Foundation of China(Grant No.11604284)and the National Natural Science Foundation of China(Grant No.11474020).

†Corresponding author.E-mail:suenyangu@163.com