反应物分子初始振动激发对H+CH+→C++H2反应的影响∗
2017-08-07唐晓平和小虎周灿华杨阳
唐晓平 和小虎周灿华 杨阳
1)(中国科学院大连化学物理研究所,分子反应动力学国家重点实验室,大连 116023)
2)(太原科技大学应用科学学院物理系,太原 030024)
3)(中国科学院大连化学物理研究所,中国科学院化学激光重点实验室,大连 116023)
反应物分子初始振动激发对H+CH+→C++H2反应的影响∗
唐晓平1)和小虎2)†周灿华3)杨阳1)
1)(中国科学院大连化学物理研究所,分子反应动力学国家重点实验室,大连 116023)
2)(太原科技大学应用科学学院物理系,太原 030024)
3)(中国科学院大连化学物理研究所,中国科学院化学激光重点实验室,大连 116023)
(2017年3月2日收到;2017年4月14日收到修改稿)
在CH+2体系的电子基态势能面上运用准经典轨线方法,研究了当碰撞能E=500 meV时,反应物分子的振动激发对H(2S)+CH+(X1Σ+)→C+(2P)+H2(X1Σ+g)反应的反应概率、反应截面和立体动力学性质的影响.分别计算了两矢量相关k-j′的P(θr)分布,三矢量相关k-k′-j′的P(φr)分布以及反应产物的四个极化微分截面.结果表明,产物分子转动角动量不仅在Y轴方向有取向效应,还定于Y轴的正方向.并且发现,随着振动量子数的增加,对反应体系产物分布的影响就越明显.
立体动力学,准经典轨线方法,矢量相关
1 引 言
H原子[1]与CH+碰撞时发生的抽取反应在天体物理中占有很重要的地位,反应的产物为C+和H2.而在该反应式 H+CH+→ C++H2中,生成产物之前需先形成短寿命的中间络合物CH+2,再由CH+2快速分离成C+和H2.自1941年CH+被首次识别以来[2],因其含量过于丰富一直备受关注.多年来,有关CH+2体系的研究颇受重视[2−11].例如:1986年Ervin 和Armentrout[10]报道了C++H2(D2,HD)→H(D)+CH+(CD+)反应的反应截面以及动力学同位素效应,主要介绍了从阈值到15 eV的碰撞区间,反应截面在给定的范围内会快速增长,并且在高能区时,还出现了同位素效应,但该效应由于振动零点能的影响呈现出了不同的结果.在实验方面,Plasil等[11]报道了低温条件下CH+与H原子在碰撞反应中,当温度为60 K时速率常数达到一个最大值,而在低于该温度时,实验值与计算的结果正好相反.最近,Werfelli等[4]基于新的势能面,运用非含时量子散射法研究了低温条件下H+CH+→C++H2反应的速率常数.结果表明,温度在50—800 K的范围内理论值与实验结果符合得很好,而当温度低于50 K时理论值远远大于实验值.Han等[12−15]运用成熟的准经典轨线法,在吸引、混合、排斥势能面上研究了产物双分子反应的转动极化.为了获得一个完整的理论动态反应,不仅要研究它的标量性质,也要重视它的矢量性质[16].最近,我们小组在研究碰撞能对CH+2体系的立体动力学性质的影响中发现[17],该反应的两矢量、三矢量分布在低能区时随碰撞能的增加而减弱,但在高能区时随碰撞能的增大该类分布却明显增强.由此可见,碰撞能对CH+2体系的影响很明显.迄今为止,尚未见有关反应物在不同的振动量子数下对CH+2体系的立体动力学性质的影响的研究.所以,本文工作主要是基于最新的势能面[18]运用准经典轨线法[19]来计算H+CH+→C++H2反应.
2 准经典轨线的方法理论
2.1 坐标系的建立
计算中采取质心坐标系来描述反应物的相对速度k和产物相对速度k′以及产物转动角动量j′的分布,如图1所示.坐标系的Z轴正方向平行于反应物相对速度矢量k的方向,Y轴垂直于含有反应物相对速度矢量k和产物相对速度矢量k′的X-Z平面,该平面也被称为散射平面.k和k′的夹角θt为散射角,分别用θr和φr来表示产物转动角动量j′的极角和方位角.

图1 描述k,k′和j′分布的质心坐标系Fig.1.The center-of-mass coordinate system used to describe the k,k′and j′correlations.
2.2 产物分子角动量的转动极化
为了对动力学信息更加直观地描述,我们计算了两矢量相关和三矢量相关的分布函数.通常产物分子k-j′两矢量相关的分布函数P(θr)可以用Legendre多项式[20−22]展开:称为定向系数(奇数)或者称为取向系数(偶数),尖括号表示求平均值.
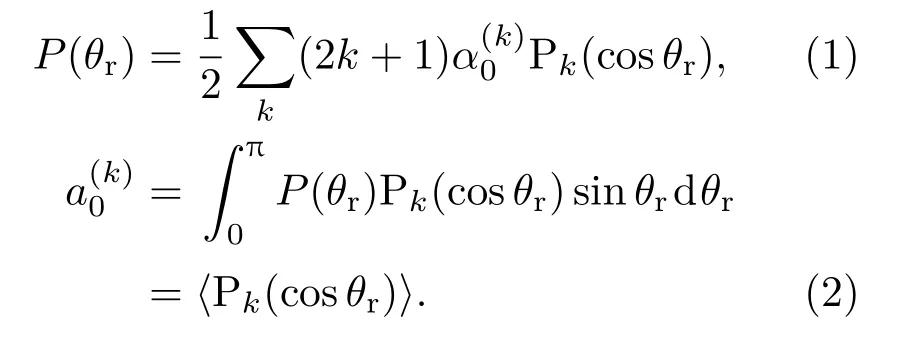
描述k,k′和j′三矢量相关二面角分布函数可以用P(φr)函数来表征,该函数可以用Fourier级数展开[23−25],即
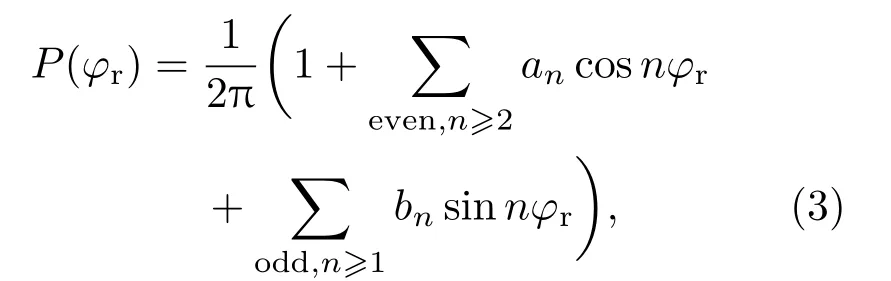
其中,αn和bn分别为
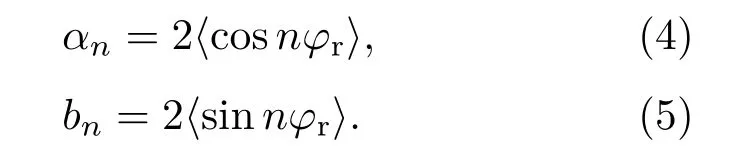
在计算过程中,为保证P(φr)收敛则取n=24即可.
定义产物转动角动量j′的空间分布函数P(θr,φr)可以表示为
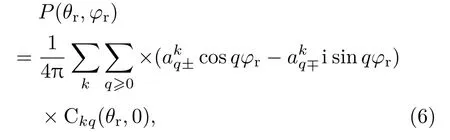
其中,Ckq(θr,φr)是修正的球谐函数,计算过程中P(θr,φr)展开到k=7便呈现出良好的收敛结果.
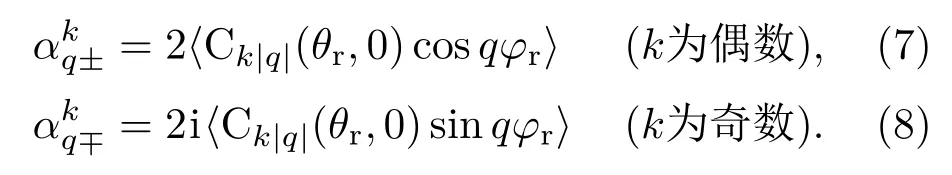
联系k,k′和j′三矢量角分布函数可以写为
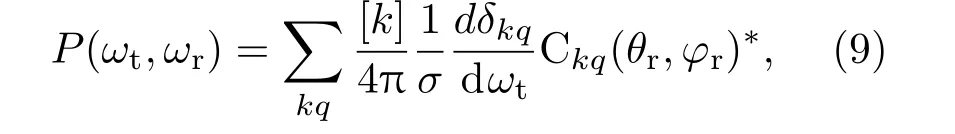

在很多光诱导的双分子反应实验中,人们只对k=0和k=2的极化微分截面感兴趣,因此只计算了(2π/σ)(dσ00/dωt),(2π/σ)(dσ20/dωt),(2π/σ)(dσ22+/dωt),(2π/σ)(dσ22−/dωt)四个极化微分反应截面.为了保证收敛,在计算中极化微分反应截面展开到k=7.
2.3 势能面
采用准经典轨线法并基于最新的[18]势能面,研究了反应物分子的振动量子数对H(2S)+CH+(X1Σ+) → C+(2P)+H2(X1Σ+g)反应的立体动力学性质的影响.该反应放热量为0.496 eV(能量单位),且势阱深度超过4 eV.实验值[25]显示H2的解离能为4.751 eV,CH+的解离能[2]为4.255 eV,而在Li等[18]研究的势能面上H2和CH+的解离能分别为4.748 eV,4.255 eV.很容易看出,Li等[18]研究的势能面与实验结果非常接近,从而得出该势能面的精确度很高.
2.4 准经典轨线计算
在最新的势能面[18]上,采用准经典轨线方法进行计算.计算时,将反应物分子振动量子数分别取为v=0,1,3,5;转动量子数取为j=0,碰撞能为E=500 meV,积分步长为0.1 fs,总的轨线条数为50000;H原子和CH+离子质心间的初始距离取为15 Å,在它附近的势能值很小,约为10−10eV的能量级,因此相互作用力非常弱,可将其忽略.反应的最大碰撞参数bmax的确定方法是:先运行5000条轨线,初步确定bmax的范围,再选择用50000条轨线,逐渐增加b使其反应的轨线条数不再增加即可[21].
3 结果与分析
图2描述了H+CH+→C++H2(v=0,1,3,5,j=0)的反应概率(P00-all)随初始振动量子数的变化情况.在计算过程中,碰撞能E=500 meV,将bmax调为零可以得到反应的轨线条数,然后将其与总的轨线条数作比,可以求出每个振动量子数所对应的反应概率.从图形的整体上看,H和CH+发生正碰时的反应概率在v=1时最大,但随着激发态振动量子数的增加反应概率呈下降趋势.
图3描述了H+CH+→C++H2(v=0,1,3,5,j=0)的反应截面.我们知道,反应截面对于一个产物通道α是这样被定义的:这里Nα表示最大碰撞参数bmax的值满足反应式收敛时所对应的反应轨线条数,N表示总的轨线条数.从整体上看图3,会发现v=0激发到v=5能级时,反应截面由17.02 Å2减小到14.33 Å2.可以看出,该放能反应的反应截面最大值和最小值之间的差异很大,也就是说振动量子数对此引起的变化很明显.
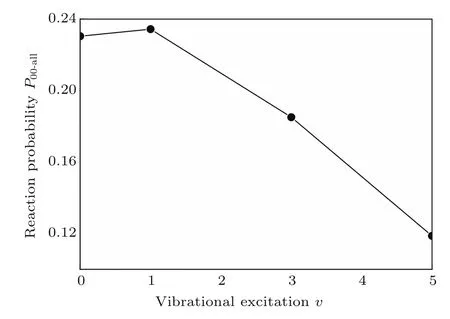
图2 不同的振动态(v=0,1,3,5)下H+CH+→C++H2反应的反应概率(P00-all)Fig.2. Reaction probability of the H+CH+ →C++H2reaction at di ff erent vibrational state(v=0,1,3,5).
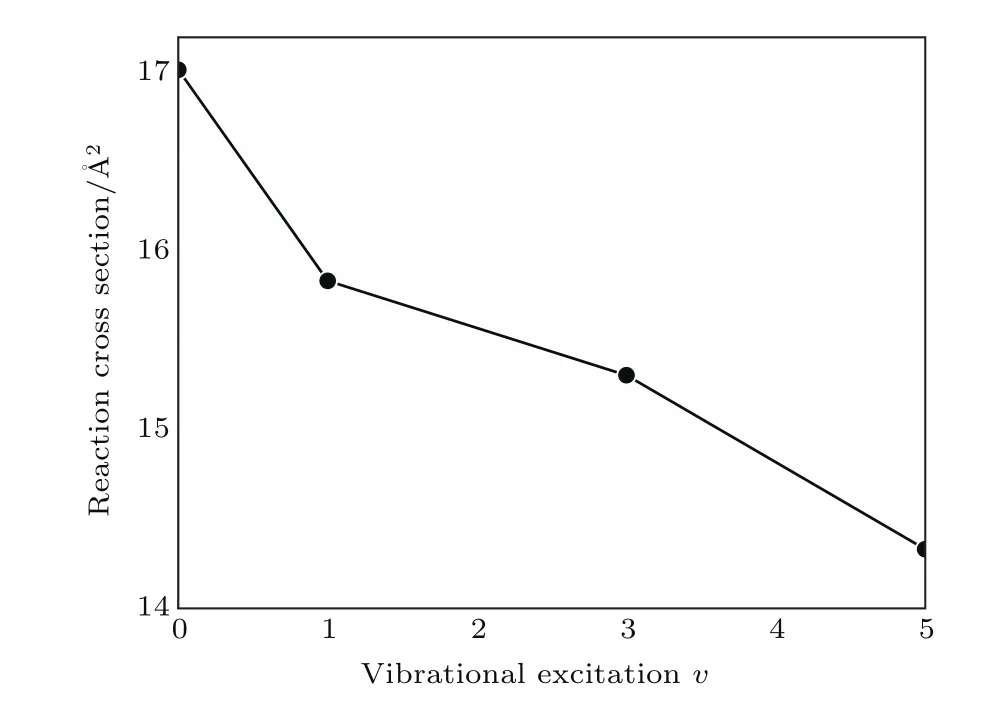
图3 不同的振动态(v=0,1,3,5)下H+CH+→C++H2反应的横截面Fig.3. Integral reaction cross section of the H+CH+→C++H2reaction at di ff erent vibrational state(v=0,1,3,5).
图4为H+CH+→C++H2反应的k-j′两矢量相关函数P(θr)的分布情况.由图4可知,函数P(θr)在θr=90◦时有一个明显的峰值,并且关于θr=90◦呈轴对称分布.这说明,产物转动角动量分布倾向于垂直矢量k的方向上.当反应物分子处于激发态时,峰值明显变大而宽度基本没有改变,这相比于基态取向效应大大增强,且随着激发态振动量子数的增加峰值的升高幅度更加明显.对CH+2体系,通过图4可以发现当v=0增加到v=5时,在θr=90◦处对应的P(θr)的峰值最低为0.56,最高达到0.7左右,增加了0.14.而在这之前本课题组研究该体系的碰撞能对此反应的影响发现[17],碰撞能由1 meV增加到1000 meV时,θr=90◦对应的P(θr)的峰值最小值为0.56,最大值为0.65,大约变化了0.09.通过比较我们不难发现,振动量子数对两矢量分布的影响比碰撞能稍大一点.
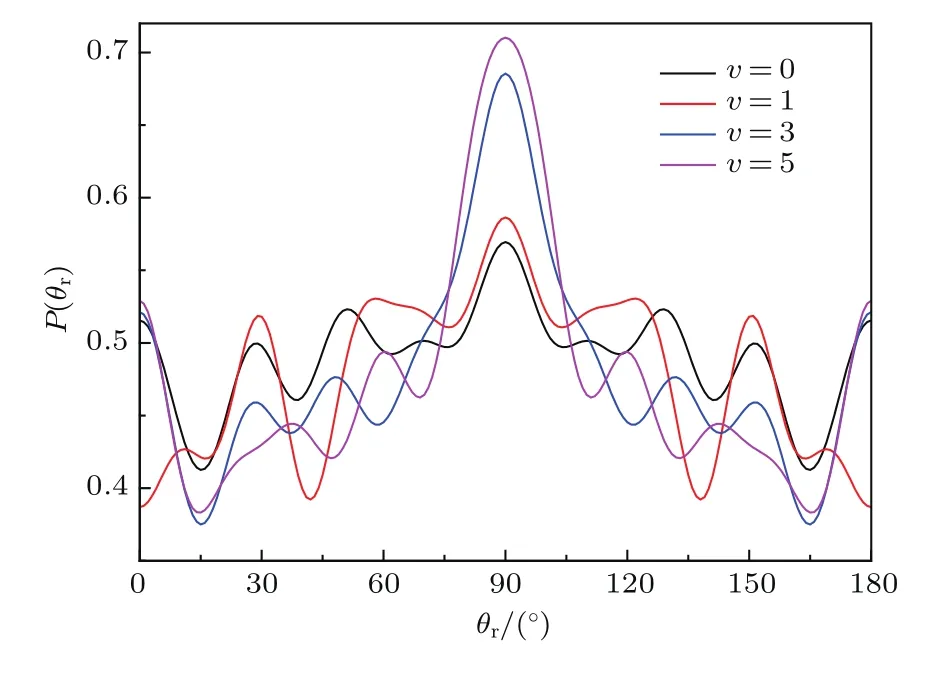
图4 (网刊彩色)不同的振动态(v=0,1,3,5)下H+CH+→C++H2反应的P(θr)分布Fig.4.(color online)Angular distribution of P(θr)the H+CH+→C++H2reaction at di ff erent vibrational state(v=0,1,3,5).
图5为H+CH+→ C++H2反应的k-k′-j′三矢量相关函数P(φr)的分布情况.如图5所示,P(φr)分布关于φr=180◦不对称,反映了产物转动角动量的强烈极化效应.在φr=90◦时,基态情况(v=0)下有峰值出现,但峰值不是很明显.而在激发态(v=1,3,5)情况下,此处的峰值随振动量子的增加逐渐增大,当振动量子数v=5时峰值达到最大.在φr=270◦处,基态时峰值基本处于平缓状态,而激发态处的峰值高于基态,但随着振动量子数的增加峰值无规律变化,且在v=1处峰值最大.总体对比后发现,在φr=90◦处的峰值要高于φr=270◦处的峰值,这也说明了产物分子转动角动量j′不仅沿着Y轴有取向分布,还定向于Y轴的正方向并且定向效应非常强.这种既有定向又有取向的分布情况可以用三原子反应的排斥模型[26]来解释.
图6为H+CH+→C++H2反应的产物转动角动量的空间分布函数P(θr,φr).图6(a)—(d)分别对应振动激发(v=0,1,3,5)的空间分布情况.为了便于比较,我们将图中的概率分布的显示范围全部调整为0.04—0.20区间段.从图6可以看出,θr=90◦和φr=270◦处P(θr,φr)有明显大小不同的峰值,四幅图中θr=90◦的峰值都比φr=270◦处的峰值高,并且随着反应物初始振动量子数的增加,峰值变得更高,同时增高的程度也变得更明显.当反应物分子处于基态(v=0)和较低的振动激发态(v=1)时,如图6(a)和图6(b)所示,发现φr=270◦处的峰值非常小,这说明初始反应物分子的振动激发对产物分子的转动定向效应的影响不大.而图6(c)和图6(d)中峰值却很明显,此时的反应物振动量子数分别为v=3和v=5.因此,随着振动量子数的增加该分布也变得越来越集中,这说明产物的转动角动量的转动极化程度随之增强.反应产物的空间分布P(θr,φr)与图4中P(θr)分布和图5中P(φr)分布结果完全对应.
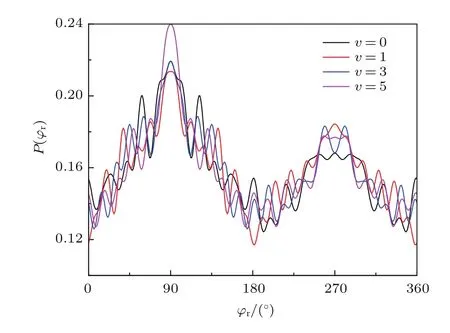
图5 (网刊彩色)不同的振动态(v=0,1,3,5)下H+CH+→C++H2反应的P(φr)分布Fig.5.(color online)Angular distribution of P(φr)the H+CH+→C++H2reaction at di ff erent vibrational state(v=0,1,3,5).
图7表示的是不同振动激发(v=0,1,3,5)下,H+CH+→C++H2反应的极化微分反应截面的分布情况.极化微分反应截面是描述k-k′-j′三矢量相关或者产物的散射方向,与产物转动角动量的定向和取向无关. 图7(a)中(2π/σ)(dσ00/dωt)只与反应物及其产物的相对速度矢量有关,我们不难发现产物分子有明显的前向和后向散射,且随振动量子数的增加前向散射和后向散射程度有减弱的趋势. 极化微分反应截面分量(2π/σ)(dσ20/dωt)在图7(b)中给出,与图7(a)曲线具有相反的分布趋势.极化微分反应截面(2π/σ)(dσ20/dωt)的分布情况也表明了j′分布取向于垂直k的方向.
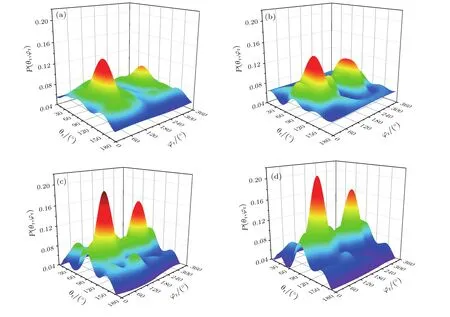
图6 (网刊彩色)不同的振动态下H+CH+→C++H2反应的空间分布P(θr,φr) (a)v=0;(b)v=1;(c)v=3;(d)v=5Fig.6.(color online)Spatial distribution of P(θr,φr)of the H+CH+→ C++H2reaction at di ff erent vibrational state:(a)v=0;(b)v=1;(c)v=3;(d)v=5.
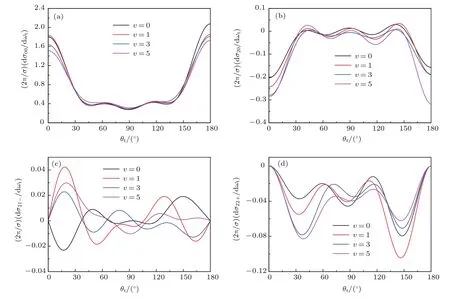
图7 (网刊彩色)不同的振动态(v=0,1,3,5)下H+CH+→ C++H2反应的极化微分反应截面 (a)(2π/σ)(dσ00/dωt);(b)(2π/σ)(dσ20/dωt);(c)(2π/σ)(dσ21−/dωt);(d)(2π/σ)(dσ22+/dωt)Fig.7.(color online)Four polarization dependent di ff erential cross-sections of the H+CH+→C++H2reaction at di ff erent vibrational state:(a)(2π/σ)(dσ00/dωt);(b)(2π/σ)(dσ20/dωt);(c)(2π/σ)(dσ21−/dωt);(d)(2π/σ)(dσ22+/dωt).
前面的两个截面(图7(a)和图7(b))均为q=0的情况, 对于q=0时如图7(c)和图7(d)所示,(2π/σ)(dσ21−/dωt),(2π/σ)(dσ22+/dωt)的极化微分反应截面在极端向前和极端向后散射的值为零.因在这些极限散射角的情况k-k′的平面不确定,故q̸=0时的极化微分反应截面的值必为零.在图7(c)中的四个振动能级下,(2π/σ)(dσ21−/dωt)值有正有负,没有较强的极化效应,因此振动量子数对该分布的影响较小. 从图7(d)可见(2π/σ)(dσ22+/dωt)在整个角分布里是负值,这表明产物更倾向于Y轴方向分布.每个反应都有三个强极化,三个极化角分别在30◦,90◦,和150◦附近最为强烈,随着振动能级的变化,v=1时取向效应最明显.
4 结 论
本文采用准经典轨线法,在最新的势能面[18]上对H(2S)+CH+(X1Σ+)→ C+(2P)+H2(X1Σ+g)反应的反应概率、反应截面以及立体动力学性质进行了研究.结果表明,反应概率和反应截面都随反应物的初始振动量子数的增加呈下降趋势.当碰撞能E=500 meV时,理论计算的两矢量、三矢量以及空间分布情况均随着振动量子数的增加,产物的转动角动量更倾向于Y轴的方向,并且定向于Y轴的正方向.同样极化微分反应截面也随着振动量子数的变化而变化,文中还描述了四个极化微分反应截面的变化情况,(2π/σ)(dσ00/dωt)随振动量子数的增加前向散射和后向散射均减弱,(2π/σ)(dσ20/dωt)的分布与(2π/σ)(dσ00/dωt)曲线变化的趋势相反,而(2π/σ)(dσ21−/dωt)没有较强的极化,(2π/σ)(dσ22+/dωt)的分布有三个强极化,且随着振动量子数的增加三个强极化的程度也有明显的变化.综上所述,该反应的立体动力学性质对振动量子数有很强的依赖性.
[1]Federer W,Villinger H,Howorka F,Lindinger W,Tosi P,Bassi D,Ferguson E 1984 Phys.Rev.Lett.52 2084
[2]Stoecklin T,Halvick P 2005 Phys.Chem.Chem.Phys.7 2446
[3]Lique F,Werfelli G,Halvick P,Stoecklin T,Faure A,Wiesenfeld L,Dagdigian P J 2013 J.Chem.Phys.138 204314
[4]Werfelli G,Halvick P,Honvault P,Kerkeni B,Stoecklin T 2015 J.Chem.Phys.143 114304
[5]Zanchet A,Godard B,Bulut N,Roncero O,Halvick P,Cernicharo J 2013 Astrophys.J.766 80
[6]Grozdanov T,McCarroll R 2013 Chem.Phys.Lett.575 23
[7]Halvick P,Stoecklin T,Larrégaray P,Bonnet L 2007 Phys.Chem.Chem.Phys.9 582
[8]Warmbier R,Schneider R 2011 Phys.Chem.Chem.Phys.13 10285
[9]Herráez-Aguilar D,Jambrina P,Menéndez M,Aldegunde J,Warmbier R,Aoiz F 2014 Phys.Chem.Chem.Phys.16 24800
[10]Ervin K M,Armentrout P B 1986 J.Chem.Phys.84 6738
[11]Plasil R,Mehner T,Dohnal P,Kotrik T,Glosik J,Gerlich D 2011 Astrophys.J.737 60
[12]Chen M D,Han K L,Lou N Q 2002 Chem.Phys.Lett.357 483
[13]Wang M L,Han K L,He G Z 1998 J.Chem.Phys.109 5446
[14]Tang B Y,Chen M D,Han K L,Zhang Z H 2001 J.Chem.Phys.115 731
[15]Chen M D,Han K L,Lou N Q 2003 J.Chem.Phys.118 4463
[16]Liu Y F,He X H,Shi D H,Sun J F 2011 Chin.Phys.B 20 078201
[17]Tang X P,Zhou C H,He X X,Yu D Q,Yang Y 2017 Acta Phys.Sin.66 023401(in Chinese)[唐晓平,周灿华,和小虎,于东麒,杨阳2017物理学报66 023401]
[18]Li Y Q,Zhang P Y,Han K L 2015 J.Chem.Phys.142 124302
[19]Liu S L,Shi Y 2011 Chin.Phys.B 20 013404
[20]Yang H,Liu Z,Sun S,Li L,Du H C,Hu B 2011 J.Theor.Comput.Chem.10 75
[21]Wu V W K 2011 Phys.Chem.Chem.Phys.13 9407
[22]Kong H,Liu X G,Xu W W,Zhang Q G 2009 Acta Phys.-Chim.Sin.25 935(in Chinese)[孔浩,刘新国,许文武,张庆刚2009物理化学学报25 935]
[23]Ma J J,Zhang Z H,Cong S L 2006 Acta Phys.-Chim.Sin.22 972(in Chinese)[马建军,张志红,丛书林2006物理化学学报22 972]
[24]Wu J C,Wang M S,Yang C L,Li X H,Chen X Q 2011Chin.Phys.Lett.28 063401
[25]Balakrishnan A,Smith V,Stoiche ffB 1992 Phys.Rev.Lett.68 2149
[26]Han K L,He G Z,Lou N Q 1998 Chin.J.Chem.Phys.11 525(in Chinese)[韩克利,何国钟,楼南泉1998化学物理学报11 525]
PACS:34.50.Lf,31.15.xv,87.15.H–DOI:10.7498/aps.66.123401
E ff ect of reagent vibrational excitation on reaction of H+CH+→ C++H2∗
Tang Xiao-Ping1)He Xiao-Hu2)†Zhou Can-Hua3)Yang Yang1)
1)(State Key Laboratory of Molecular Reaction Dynamics,Dalian Institute of Chemical Physics,Chinese Academy of Sciences,Dalian 116023,China)
2)(School of Applied Science,Taiyuan University of Science and Technology,Taiyuan 030024,China)
3)(Key Laboratory of Chemical Lasers,Dalian Institute of Chemical Physics,Chinese Academy of Science,Dalian 116023,China)
2 March 2017;revised manuscript
14 April 2017)
The e ff ect of reagent vibrational excitation on the stereodynamical properties of H(2S)+CH+(X1Σ+) →C+(2P)+H2(X1Σ+g)reaction is investigated by quasi-classical trajectory method on a globally smooth ab initio potential surface of the 2A′state at a collision energy of 500 meV.The reaction probability and the reaction cross-section are also studied.In the calculation,the vibrational levels of the reactant molecules are taken as v=0,1,3,5 and j=0,respectively,where v is the vibrational quantum number and j is the rotational quantum number.The calculation results show that the reaction probability reaches a maximum when v=1,and then decreases with the vibrational quantum number increasing.The integral cross-section decreases sharply with the increase of vibrational quantum number.The potential distribution P(θr),the dihedral angle distribution P(φr),and the polarization-dependent generalized di ff erential cross sections are calculated.P(θr)represents the relation between the reagent relative velocity k and the product rotational angular momentum j′.P(φr)describes the correlation of k-k′-j′,in which k′is the product reagent relative velocity.The peak of P(θr)is at θr=90◦and symmetric with respect to 90◦,which shows that the product rotational angular momentum vector is strongly aligned along the direction perpendicular to the relative velocity direction.The peak of P(θr)distribution becomes increasingly obvious with the increase of the rotational quantum number.The dihedral angle distribution P(φr)tends to be asymmetric with respect to the k-k′scattering plane(or about φr=180◦),directly re fl ecting the strong polarization of the product angular momentum for the title reaction.Each curve has two evident peaks at about φr=90◦and φr=270◦,but the two peak intensities are obviously di ff erent,which suggests that j′is not only aligned,but also strongly orientated along the Y-axis of the center-of-mass frame.The peak at φr=90◦is apparently stronger than that at φr=270◦,which indicates that j′tends to be oriented along the positive direction of Y-axis.In order to validate more information,we also plot the angular momentum polarization in the forms of polar plots θrand φr.The distribution of P(θr,φr)is well consistent with the distribution P(θr)and also the distribution P(φr)of the products at di ff erent vibrational quantum states.In addition,the polarization-dependent di ff erential cross section is quite sensitive to the reagent vibrational excitation.Based on the obtained results,we fi nd that the observed excess of the methylidyne cation CH+is closely related to the reactant of vibrational excitation in interstellar chemistry.
molecular reaction dynamics,quasi-classical trajectory method,vector correlation
10.7498/aps.66.123401
∗国家自然科学基金(批准号:21403226,21503226)资助的课题.
†通信作者.E-mail:huzi233@126.com
©2017中国物理学会Chinese Physical Society
http://wulixb.iphy.ac.cn
*Project supported by the National Natural Science Foundation of China(Grant Nos.21403226,21503226).
†Corresponding author.E-mail:huzi233@126.com
