运用改进的无单元Galerkin方法分析机场道面断裂力学问题∗

邹诗莹 席伟成 彭妙娟 程玉民†

1)(上海大学上海市应用数学和力学研究所,上海 200072)

2)(上海大学土木工程系,上海 200444)

运用改进的无单元Galerkin方法分析机场道面断裂力学问题∗

邹诗莹1)席伟成2)彭妙娟2)程玉民1)†

1)(上海大学上海市应用数学和力学研究所,上海 200072)

2)(上海大学土木工程系,上海 200444)

(2017年2月26日收到;2017年3月26日收到修改稿)

在改进的无单元Galerkin方法的基础上,将能反映裂纹尖端附近应力奇异性的特征项引入改进的移动最小二乘法的基函数中,将断裂力学和改进的无单元Galerkin方法结合,研究了线弹性断裂力学的改进的无单元Galerkin方法,并对含反射裂缝的机场复合道面层状体系结构进行了数值分析.本文的理论为机场复合道面断裂力学分析提供了一种新方法.

改进的无单元Galerkin方法,机场复合道面,层状体系,反射裂缝

1 引 言

无网格方法的研究已有二十多年的历史,国际上目前将基于点的近似构造试函数、不需要考虑节点与单元间关联条件的各种数值方法称为无网格方法[1,2].

程玉民等[3,4]在移动最小二乘法的基础上,建立了改进的移动最小二乘法. 引入复变量理论,程玉民等建立了复变量移动最小二乘法[5,6]、改进的复变量移动最小二乘法[7]和复变量重构核粒子法[8].在此基础上,提出了改进的无单元Galerkin方法[9,10]、插值型无单元Galerkin方法[11−14]、边界无单元法[15−18]、复变量无单元Galerkin方法[19−23]、改进的复变量无单元Galerkin方法[7,24−26]和复变量重构核粒子法[8,27−29].

由于改进的移动最小二乘法形成的方程组易于求解并且不形成病态方程组,因而改进的无单元Galerkin方法可以提高无单元Galerkin方法的计算精度和计算效率.

机场复合道面兼顾了刚性路面和柔性路面的优点.水泥混凝土板提供了一个稳定、坚实的基础,沥青混凝土则作为表面功能特性优良的磨耗层.然而,在水泥混凝土板间各种形式的接缝或裂缝使得加铺的沥青面层易产生反射裂缝.在沥青混凝土加铺层出现反射裂缝后,会使地表水进入沥青混合料内部,从而降低集料与沥青之间的黏结性能,形成松散、剥落等病害.特别是在飞机轮载的作用下容易导致应力集中现象,反射裂缝周边道面又会形成新的交叉次生裂缝,发展到一定程度后将使道面出现大面积剥落,严重影响飞机的运行安全.反射裂缝是机场复合道面破坏的主要表现形式之一.

关于机场复合道面反射裂缝,Garzon等[30,31]利用三维广义有限元法对荷载作用下机场道面的反射裂缝进行了研究;李淑明等[32]采用有限元法分析了土工布、玻璃纤维网对旧水泥混凝土路面加铺沥青混凝土层复合路面结构的内力影响;凌建明等基于弹性层状体系理论,利用有限元法对飞机荷载作用下机场道面地基附加应力进行了分析[33],提出了机场复合道面剩余寿命预估方法[34];马翔等以B777-200飞机荷载为计算荷载,利用有限元法分析了复合机场道面荷载应力[35],提出了以荷载与温度综合疲劳弯拉应力和沥青面层反射裂缝疲劳寿命为设计指标的复合机场道面结构设计方法[36].

综上研究进展,目前关于机场复合道面反射裂缝的计算均采用有限元法,尚未见到采用无网格方法分析机场复合道面反射裂缝,而无网格方法在求解断裂问题方面优于有限元法.因而,对机场复合道面来说,研究应用于反射裂缝分析的断裂力学的无网格方法是非常必要的.

2 改进的移动最小二乘法

在移动最小二乘法中,取函数u(x)的逼近函数为

其中m是基函数的个数,pi(x)是基函数,ai(x)是相应的系数.

对应于(1)式的整体逼近,在点x邻域内的局部逼近定义为

其中xI为影响域覆盖点x的节点,n是影响域覆盖点x的节点数,uI=u(xI).

对J取极值,即得

可得

即

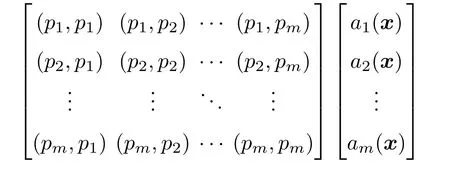
对于点集{xi}和权函数{wi},若一组函数φ1(x),φ2(x),···,φm(x)满足

则称φ1(x),φ2(x),···,φm(x)是关于点集{xi}带权{wi}的正交函数族(k,j=1,2,···,m).

若{pi(x)},i=1,2,···,m,为Hilbert空间span(p)上的关于点集{xi}的带权的正交基函数族,即

则方程(6)可写成

这样,我们可以直接得到系数ai(x),即

写成矩阵形式

其中

将(10)式代入(2)式可得

其中Φ∗(x)为形函数,

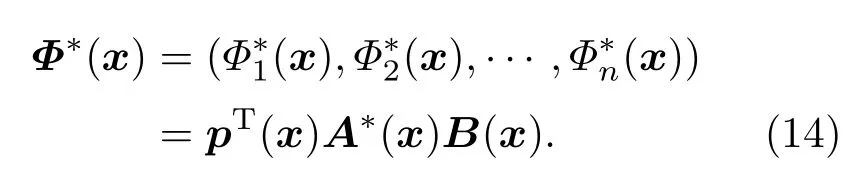
这样,系数ai(x)可以简单、直接地得到,不需要求矩阵A(x)的逆,避免了求解病态或奇异的方程组,既提高了效率,又提高了精度.

对如下基函数

利用Schmidt正交化方法得到的正交基函数为

3 裂纹尖端试函数

基函数扩展法是通过在基函数中加入扩展函数项,来达到对试函数扩展的目的.对于断裂力学的改进的无单元Galerkin方法,基函数中必须加入裂纹尖端位移场表达式中的一些重要项和一些重要的梯度项.基函数扩展的项数决定了数值解的精度,当基函数中加入了能反映包含裂纹尖端位移场中的所有项,即完全基函数扩展时,取如下形式:

类似于改进的移动最小二乘法的推导,可得

类似(13)式可得裂纹尖端试函数为

由此可以看出基函数扩展法没有增加新的节点未知变量.但是由于基函数的项数增加了,形函数的计算量也会相应地增加.为了提高计算效率,本文采用局部基函数扩展法,即在基函数中加入即

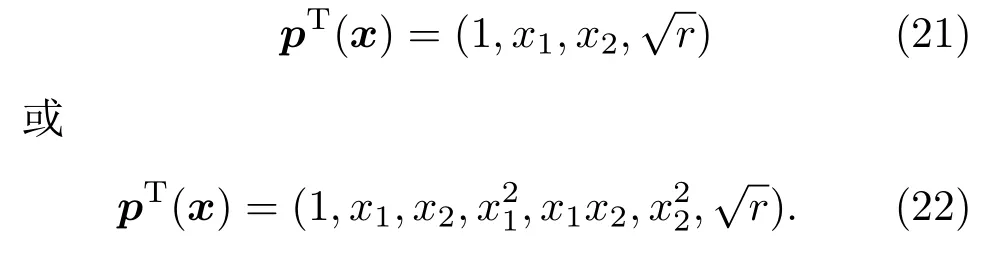
这样,可以得到裂纹尖端的试函数为

可得裂纹尖端节点的形函数

4 断裂力学的改进的无单元Galerkin方法

假设二维弹性体的求解域为Ω,边界为Γ,弹性力学问题的平衡方程为

其中σij为应力分量,bi是单位体积上的体力分量,i,j=1,2.

几何方程为

其中εij是应变分量,ui是位移分量.

本构方程为

式中D=(Dijkl)是弹性矩阵,对于平面应力问题,

对于平面应变问题,

其中E为材料的弹性模量.

对应的边界条件为

本节采用罚函数法施加本质边界条件,则弹性力学问题对应的泛函为

如果位移边界条件是沿xi方向的,则si为0,否则为1.

将求解域离散为有限个节点,节点总数为M.利用改进的移动最小二乘法建立逼近函数,可得位移的逼近函数为

对非裂纹尖端节点,形函数如(14)式所示;裂纹尖端节点的形函数见(24)式.

将(37)式代入(32)式,可得

矩阵Kα是根据节点信息得到的全局罚函数矩阵,

向量Fα由本质边界条件得到,

裂缝尖端的应力强度因子采用以下方法进行计算.对裂纹尖端选取适当的|OC|=L得点C,|OB|=L/4得点B.由点O,B,C即构成二维问题裂纹尖端的虚拟奇异二次元,裂纹尖端局部坐标如图1所示,应力强度因子表达式为

其中a为裂纹长度的一半,vB和vC分别为点B和点C竖直方向的位移.

图1 裂纹尖端虚拟奇异元Fig.1.The virtual singular element at the tip of a crack.

5 机场道面反射裂缝的数值分析

5.1 机场复合道面反射裂缝的计算模型

为了进行反射裂缝影响因素分析,将复合机场道面结构简化为平面应变问题的层状体系,采用二维模型进行数值计算.将荷载简化为二维平面应变问题下的条形均布荷载,采用B777-200B,轮压为1.45 MPa,轮距为1.40 m.此外假定各结构层都由线弹性的各向同性、均质材料组成,地基由弹性半空间地基假设,在模型中采用有限尺寸.模型的边界条件为:地基底部完全约束,各结构层两侧铰接,具体几何参数如图2,各层的物理参数见表1,反射裂缝起裂位置如图3,裂缝宽度取0.5 cm.

图2 机场复合道面模型几何参数(mm)Fig.2.The geometric parameters of the airport composite pavement(mm).

表1 结构的物理参数Table 1.The physical parameters of the structure.

图3 反射裂缝的位置Fig.3.The position of the re fl ective crack.

5.2 机场复合道面反射裂缝力学分析

首先考虑起裂位置处于接缝处的裂缝计算模型.无网格方法的节点布置采用5370个节点,轮载下方区域节点进行加密,并对起裂位置进行局部加密,沿水泥板接缝位置布置2×27个加密节点,具体节点分布和局部加密如图4和图5.

图4 模型节点布置Fig.4.The node distribution of the model.

图5 裂缝附近节点加密分布(2×27)Fig.5.The node re fi nement distribution at the tip of the crack(2×27).

计算结束后,选取裂纹尖端适当计算点,采用(47)式计算,得到此处应力强度因子KI为9.42 MPa·mm1/2,裂缝尖端位于混凝土板层,回弹模量为30000 MPa.

在此基础上,进一步考虑裂缝反射到沥青加铺层的反射裂缝模型,如图6取反射至沥青面层的裂缝长度为4 cm,并在裂纹区域进行节点加密(3×31个加密节点),其节点布置局部如图7所示.

通过计算得到的KI为0.36 MPa·mm1/2,裂缝尖端位于沥青层,回弹模量为2000 MPa.

图6 反射至沥青层的裂缝Fig.6.The re fl ective crack in the asphalt layer.

图7 反射裂缝附近节点加密分布(3×31)Fig.7.The node re fi nement distribution at the tip of the re fl ective crack(3×31).

图8 沥青层计算点竖向位移Fig.8.The vertical displacement at the points in the asphalt layer.

选取计算点后对模型的位移和应力进行计算,计算结果如图8—图10所示.从图8可以看出,在荷载作用位置附近,竖向位移较大,与路面实际情况符合.从图9可以看出,当混泥土板开裂后,在荷载作用下裂缝正上方面层的正应力具有奇异性,从而使得路面反射裂缝继续向上发展,以致最后贯通整个路面.可见,当基层出现裂缝后,由于裂缝尖端存在一定的应力集中,这种应力集中对于路面正常工作是不利的.所以,路面工程施工中要尽可能减少混凝土板的收缩裂缝,以防止反射裂缝发生.

从图9和图10可以看出,在对称荷载作用下,裂缝尖端正应力远大于剪应力,裂缝为张开型,即裂缝的扩展受正应力或KI的控制.

图9 轮载下各层计算点正应力σ11Fig.9.The normal stress σ11at the points in layers under the wheel load.

图10 轮载下各层计算点剪应力τ21Fig.10.The shear stress τ21at the points in layers under the wheel load.

6 结 论

本文针对机场复合道面的反射裂缝问题,建立了断裂力学改进的无单元Galerkin方法.数值算例表明,该方法通过对试函数的扩展能有效地反映裂纹尖端应力场的奇异性,提高了无网格方法的求解精度.

在对试函数进行改进时,采用基函数的局部扩展法,不仅能有效地提高对裂纹尖端应力场的计算精度,也比试函数外部扩展法以及基函数完全扩展法具有更好的求解效率.

使用改进无单元Galerkin方法对机场复合道面模型进行计算,在布置节点时,在裂纹局部进行加密布置.对于计算裂纹扩展的模型时,可以在扩展路径的区域内增加布置相应的节点,而无需进行有限元法的网格重构.

本文的理论为机场复合道面反射裂缝的分析提供了一种新的方法.

[1]Cheng Y M 2015 Meshless Methods(Beijing:Science Press)pp1–13(in Chinese)[程玉民2015无网格方法 (北京:科学出版社)第1—13页]

[2]Cheng Y M,Ji X,He P F 2004 Acta Mech.Sin.36 43(in Chinese)[程玉民,嵇醒,贺鹏飞 2004力学学报 36 43]

[3]Cheng Y M,Chen M J 2003 Acta Mech.Sin.35 181(in Chinese)[程玉民,陈美娟 2003力学学报 35 181]

[4]Cheng Y M,Liew K M,Kitipornchai S 2009 Int.J.Numer.Meth.Eng.78 1258

[5]Cheng Y M,Peng M J,Li J H 2005 Chin.J.Theor.Appl.Mech.37 719(in Chinese)[程玉民,彭妙娟,李九红2005应用力学学报37 719]

[6]Cheng Y M,Li J H 2005 Acta Phys.Sin.54 4463(in Chinese)[程玉民,李九红 2005物理学报 54 4463]

[7]Bai F N,Li D M,Wang J F,Cheng Y M 2012 Chin.Phys.B 21 020204

[8]Chen L,Cheng Y M 2008 Acta Phys.Sin.57 1(in Chinese)[陈丽,程玉民 2008物理学报 57 1]

[9]Peng M J,Li R X,Cheng Y M 2014 Eng.Anal.Bound.Elem.40 104

[10]Cheng R J,Cheng Y M 2016 Chin.Phys.B 25 020203

[11]Sun F X,Wang J F,Cheng Y M 2013 Chin.Phys.B 22 120203

[12]Cheng Y M,Bai F N,Peng M J 2014 Appl.Math.Modell.38 5187

[13]Cheng Y M,Bai F N,Liu C,Peng M J 2016 Int.J.Comput.Mater.Sci.Eng.5 1650023

[14]Sun F X,Wang J F,Cheng Y M 2016 Int.J.Appl.Mech.8 1650096

[15]Cheng Y M,Peng M J 2005 Sci.China Ser.G 48 641

[16]Peng M J,Cheng Y M 2009 Eng.Anal.Bound.Elem.33 77

[17]Ren H P,Cheng Y M,Zhang W 2009 Chin.Phys.B 18 4065

[18]Wang J F,Wang J F,Sun F X,Cheng Y M 2013 Int.J.Comput.Meth.10 1350043

[19]Cheng Y M,Li J H 2006 Sci.China Ser.G 49 46

[20]Peng M J,Li D M,Cheng Y M 2011 Eng.Struct.33 127

[21]Li D M,Peng M J,Cheng Y M 2011 Sci.Sin.:Phys.Mech.Astron.41 1003(in Chinese)[李冬明,彭妙娟,程玉民2011中国科学:物理学力学 天文学41 1003]

[22]Cheng Y M,Li R X,Peng M J 2012 Chin.Phys.B 21 090205

[23]Cheng Y M,Wang J F,Li R X 2012 Int.J.Appl.Mech.4 1250042

[24]Cheng Y M,Wang J F,Bai F N 2012 Chin.Phys.B 21 090203

[25]Deng Y J,Liu C,Peng M J,Cheng Y M 2015 Int.J.Appl.Mech.7 1550017

[26]Cheng Y M,Liu C,Bai F N,Peng M J 2015 Chin.Phys.B 24 100202

[27]Chen L,Ma H P,Cheng Y M 2013 Chin.Phys.B 22 050202

[28]Weng Y J,Cheng Y M 2013 Chin.Phys.B 22 090204

[29]Chen L,Cheng Y M,Ma H P 2015 Comput.Mech.55 591

[30]Garzon J,Duarte C A,Buttlar W 2010 Road Mater.Pavement Design 11 459

[31]Garzon J,Kim D,Duarte C A 2013 Int.J.Comput.Meth.10 1350045

[32]Li S M,Cai X M,Xu Z H 2005 J.Tongji Univ.(Nat.Sci.)33 1616(in Chinese)[李淑明,蔡喜棉,许志鸿 2005同济大学学报(自然科学版)33 1616]

[33]Wo R H,Ling J M 2001 J.Tongji Univ.29 288(in Chinese)[呙润华,凌建明2001同济大学学报29 288]

[34]Zhou Z F,Ling J M,Yuan J 2007 J.Traffic Transport.Eng.7 50(in Chinese)[周正峰,凌建明,袁捷 2007交通运输工程学报7 50]

[35]Ma X,Ni F J,Chen R S 2010 J.Changan Univ.(Nat.Sci.)30 23(in Chinese)[马翔,倪富健,陈荣生2010长安大学学报(自然科学版)30 23]

[36]Ma X,Ni F J,Gu X Y 2010 J.Traffic Transport.Eng.10 36(in Chinese)[马翔,倪富健,顾兴宇2010交通运输工程学报10 36]

PACS:02.60.Cb,02.60.Lj,46.50.+aDOI:10.7498/aps.66.120204

Analysis of fracture problems of airport pavement by improved element-free Galerkin method∗

Zou Shi-Ying1)Xi Wei-Cheng2)Peng Miao-Juan2)Cheng Yu-Min1)†

1)(Shanghai Institute of Applied Mathematics and Mechanics,Shanghai University,Shanghai 200072,China)
2)(Department of Civil Engineering,Shanghai University,Shanghai 200444,China)

26 February 2017;revised manuscript

26 March 2017)

Using the improved element-free Galerkin(IEFG)method,in this paper we introduce the characteristic parameterwhich can re fl ect the singular stress near the crack tip into the basic function of the improved moving least-squares(IMLS)approximation.Combining fracture theory with the IEFG method,we present an IEFG method of treating the elastic fracture problems,and analyze a numerical example of two-dimensional layered system of airport composite pavement with re fl ective crack.

In the IEFG method,the IMLS approximation is used to form the shape function.The IMLS approximation is presented from the moving least-squares(MLS)approximation,which is the basis of the element-free Galerkin(EFG)method.Compared with the MLS approximation,the IMLS approximation uses the orthonormal basis functions to obtain the shape function,which leads to the fact that the matrices for obtaining the undetermined coefficients are diagonal.Then the IMLS approximation can obtain the solutions of the undetermined coefficients directly without the inverse matrices.The IMLS approximation can overcome the disadvantages of the MLS approximation,in which the ill-conditional or singular matrices are formed sometimes.And it can also improve the computational efficiency of the MLS approximation.

Because of the advantages of the IMLS approximation,the IEFG method has greater computational efficiency than the EFG method which is based on the MLS approximation,and can obtain the solution for arbitrary node distribution,even though the EFG method cannot obtain the solution due to the ill-conditional or singular matrices in the MLS approximation.

Paving the asphalt concrete layer on the cement concrete pavement is an e ff ective approach to improving the structure and service performance of an airport pavement,which is called airport composite pavement.The airport composite pavement has the advantages of rigid pavement and fl exible pavement,but there are various forms of joints or cracks of cement concrete slab,which makes the crack re fl ect into the asphalt overlay easily under the plane load and environmental factors.Re fl ective crack is one of the main failure forms of the airport composite pavement.Therefore,it is of great theoretical signi fi cance and engineering application to study the generation and development mechanism of re fl ective crack of the airport composite pavement.

For the numerical methods of solving the fracture problems,introducing the characteristic parameterwhich can re fl ect the singular stress near the crack tip into the basic function is a general approach.In this paper,we use this approach to obtain the IEFG method for fracture problems,and the layered system of airport composite pavement with re fl ective crack is considered.The numerical results of the displacements and stresses in the airport composite pavement are given.And at the tip of the crack,the stress is singular,which makes the crack of the airport composite pavement grow.

This paper provides a new method for solving the re fl ective crack problem of airport composite pavement.

improved element-free Galerkin method,airport composite pavement,layered system,re fl ective crack

10.7498/aps.66.120204

∗国家自然科学基金委员会-中国民航局民航联合研究基金(批准号:U1433104)资助的课题.

†通信作者.E-mail:ymcheng@shu.edu.cn

©2017中国物理学会Chinese Physical Society

http://wulixb.iphy.ac.cn

*Project supported by the National Natural Science Foundation of China(Grant No.U1433104).

†Corresponding author.E-mail:ymcheng@shu.edu.cn