一维自旋1键交替XXZ链中的量子纠缠和临界指数∗

苏耀恒 陈爱民2) 王洪雷 相春环

1)(西安工程大学理学院,西安 710048)2)(西安交通大学理学院,西安 710049)

3)(重庆医科大学医学信息学院,重庆 400016)

4)(重庆医科大学公共卫生与管理学院,重庆 400016)

一维自旋1键交替XXZ链中的量子纠缠和临界指数∗

苏耀恒1)陈爱民1)2)王洪雷3)相春环4)†

1)(西安工程大学理学院,西安 710048)2)(西安交通大学理学院,西安 710049)

3)(重庆医科大学医学信息学院,重庆 400016)

4)(重庆医科大学公共卫生与管理学院,重庆 400016)

(2017年1月3日收到;2017年3月28日收到修改稿)

利用基于张量网络表示的矩阵乘积态算法以及无限虚时间演化块抽取方法,本文研究了一维无限格点自旋1的键交替反铁磁XXZ海森伯模型中的量子相变.分别计算了系统的von Neumann熵、单位格点保真度和序参量,从而得到了系统随键交替强度的变化从拓扑有序Néel相到局域有序二聚化相的量子相变点.我们用矩阵乘积态方法拟合出了相变的中心荷c≃0.5,表明此相变属于二维经典的Ising普适类.另外,通过对拓扑Néel序的数值拟合,我们得到了相变点处的特征临界指数β′=0.236和γ′=0.838.

量子相变,量子纠缠,拓扑相,临界指数

1 引 言

自从朗道引入二级相变理论以来,量子多体系统一直都是凝聚态物理学中一个非常重要的研究领域,尤其是对低维量子强关联系统中量子相变的刻画引起了相当大的关注[1].为了揭示自然界中不同物质的存在形式及性质,科学家们提出了各种不同的模型,特别是自旋为1的模型由于具有丰富的相图及复杂的物理现象而受到人们的广泛关注[2−5].在一维自旋为1的反铁磁XXZ模型中,Haldane相和Néel相是有能隙的自旋固体相,此类物质相突破了传统的金茨堡朗道对称破缺理论而被称为拓扑有序相.在拓扑相中,因受到隐性的对称性保护,虽然不具有局域序参量,但是有非局域的长程序参量存在[6−8].

在数值计算中,对于拓扑有序相的一般计算方法都是基于有限尺寸的系统做外推来得到长程序[9].这种方法的不足之处在于受到系统尺寸的限制,所得到的长程序精度不高.如果以这样的精度来刻画量子拓扑相变的临界性质就会遇到很大的困难.近年来,苏耀恒等[10]基于张量网络(tensor network,TN)表示的无限矩阵乘积态(in fi nite matrix product state,iMPS)算法[11]所发展的一种新的方法可以直接计算出大尺度体系下的长程序参量.随后,人们利用这种算法对于含有拓扑相变的系统进行了大量的研究,并揭示了其更深层次的物理内涵[12−14].为了研究量子相变的深层次含义就必须从理论上和数值上得到相变的临界指数.但是对于含有拓扑相的相变,由于不存在局域的序参量,有限算法外推来拟合临界指数就面临很大困难.因此,要想得到相变的临界指数就必须从非局域序入手.

在自旋为1的反铁磁XXZ模型中,当系统的结构对称性被打破时,系统就将从上面所提到的拓扑有序相最终转变为局域有序的二聚化相[15].就数值计算而言,还没有有效的手段从非局域序拟合出相变的各种临界指数.我们提出的刻画拓扑相的方法正好对此类相变的研究提供了一个非常有效的手段.怎样将这一手段应用到刻画量子相变的性质研究中是一个非常有意义的课题.基于此目的,本文利用iMPS算法研究在含有键交替效应的一维无限尺寸下自旋为1的XXZ海森伯模型中的非局域关联和量子相变.

2 模 型

为了研究结构对称性破缺体系的拓扑相中的非局域关联和量子相变,本文选取键交替的一维反铁磁自旋为1的XXZ海森伯模型[15],其哈密顿量可以表示为

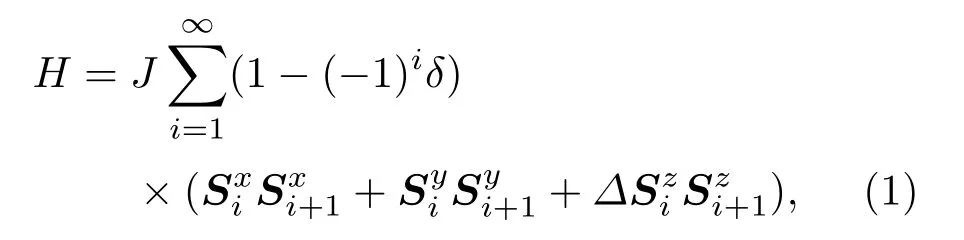
其中Si为格点i处的自旋1算符;δ是键交替幅度参数,其取值范围为δ∈[0,1];J是反铁磁的最近邻自旋相互作用强度;∆是z方向的各向异性参数.从(1)式可以看出,当δ=1时,系统达到完全的二聚化态;而当δ=0时,系统就约化为标准的XXZ海森伯模型.此时,随着各向异性参数∆的增大,系统依次出现铁磁相(∆6−1),XY相(−1< ∆ >0),Haldane相(0< ∆ 6 1.17)和Néel相(∆>1.17).这些物相中,铁磁相由局域的铁磁序参量来描述;XY相是一个无能隙的自旋液体相,而且没有任何的序参量;Haldane相和Néel相是有能隙的拓扑自旋固体相,具有长程的拓扑序参量.本文主要研究在含有键交替效应情况下Néel相(∆=2)的非局域关联和量子相变.

3 iMPS数值算法

近年来,基于张量网络表示的iMPS算法已经被成功地应用到计算一维无限格子系统的基态波函数中.此处将简要介绍iMPS算法的关键步骤.如果一个系统的哈密顿量具有平移两个格点不变性,则平移不变的iMPS态|ψ⟩就可以表示成如下形式:

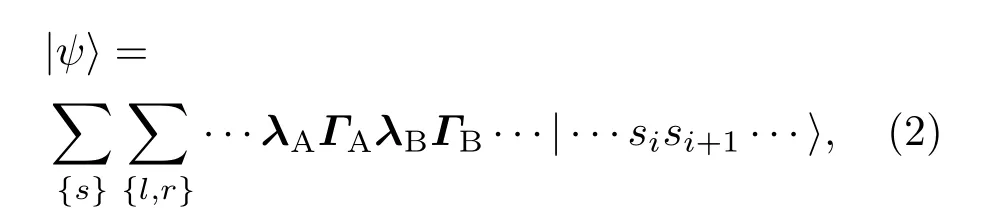
其中对角矩阵λA(B)是两半无限链的施密特分解系数;ΓA(B)是奇(偶)格点对应的三阶张量;l(r)是左(右)键对应的指标,其值可以取1,···,χ,χ是iMPS算法中截断维数;si值取为1,···,d,d是单个格点希尔伯特空间维度.对于给定的具有平移变换不变性的系统哈密顿量H和一个任意初始波函数可以利用虚时间演化方法在虚时间τ足够大的条件下,就可以得到系统的最优化数值基态波函数.在算法的迭代更新过程中,最有效的方法是对虚时间演化算符进行Suzuki-Trotter分解,使之约化为一系列只作用于两个近邻点的两点演化算符的乘积.一旦得到了无限系统的基态波函数,我们就可以将之施加在相应的物理算子上,从而计算出相应的物理量.

4 数值模拟

4.1 量子纠缠

对于一个给定的系统,量子纠缠是一种用来测量量子关联的方法.在量子信息中,人们已经采用各种不同的方式来度量系统的纠缠,包括von Neumann熵、concurrence、生成纠缠、Negativity和几何纠缠等.近年来,基于量子信息的量子纠缠已经被应用于研究量子相变.而且大量的研究也证明了量子纠缠是一个能够有效地探测系统量子相变点的普适方法[16−21].在张量网络表示下,对于一个正则形式的iMPS波函数,用来测量量子纠缠的von Neumann熵S能够被表示为[10]

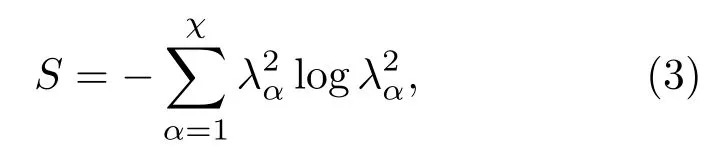
其 中λα是 两 个 半 无 限 链 链L(−∞,···,i)和R(i,···,∞)间的Schmidt分解系数,χ是iMPS算法中的截断维数.

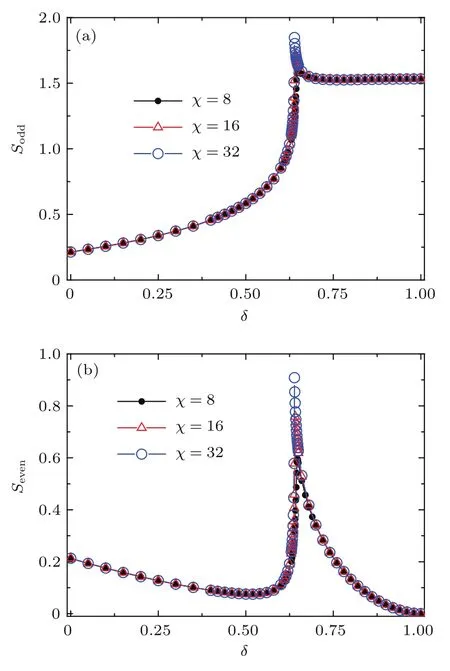
图1 (网刊彩色)截断维数χ=8,16,32时von Neumann熵随δ的变化 (a)奇键熵Sodd;(b)偶键熵SevenFig.1.(color online)von Neumann entropy as a function of δ for the truncation dimensions χ =8,16,and 32:(a)Odd-bond entropy Sodd;(b)even-bond entropy Seven.

作为对量子纠缠的测量,在图1(a)和图1(b)中,我们分别计算了系统的奇键熵Sodd和偶键熵Seven.数据表明,对于不同的截断维数χ=8,16,32,奇键熵Sodd和偶键熵Seven都出现一个奇异点,而且奇键熵Sodd和偶键熵Seven所得到的奇异点的位置是相同的,这个奇异点就对应着系统控制参量δ的改变所产生的相变点.随着截断维数χ的增加,相变点也随之发生移动.实际上,如果我们想得到系统的真实相变点,截断维数χ必须达到无穷大.但是从数据里可以看到,当截断维数增加到χ=32时,相比于χ=16的奇键熵Sodd和偶键熵Seven,所得到的相变点几乎重合.因此,我们就判定χ=32所得到的相变点δc=0.638可以作为系统的相变点,而且这也能够保证接下来的数据结果的精度是可靠的.同时,这也说明了度量量子纠缠的von Neumann熵能够被用来探测此系统的量子相变.另外,从图1我们也可以看出,奇键熵Sodd和偶键熵Seven在整个参数范围内的值是不同的.这表明在标准的XXZ模型中加入键交替效应后,系统就被二聚化了.特别是在拥有长程拓扑关联的Néel相(δ<0.638)中,这种二聚化效应也是存在的.一旦键交替参数δ超过δc=0.638时,系统就过渡到典型的二聚化态.当键交替参数δ逐渐增大到1,偶键熵Seven的值逐渐降低到零,奇键熵Sodd逐渐饱和.最终系统出现完全的奇键二聚化.

4.2 量子单位格点保真度

和量子纠缠不同,量子信息理论中的保真度被用来测量两个量子态的相似程度.从另一个方面来说,金茨堡-朗道理论中的序参量方法是和模型相关的,这是因为对于不同的模型必须找到相对应形式的序参量才能明确地刻画系统的相变.但是近几年的研究表明,量子单位格点保真度是一个不依赖于模型的探测量子相变的方法[22−24].具体到iMPS算法的保真度计算,一旦得到了系统在不同的键交替参数δ下的基态波函数,单位格点的基态保真度d(δ1,δ2)就可以定义为

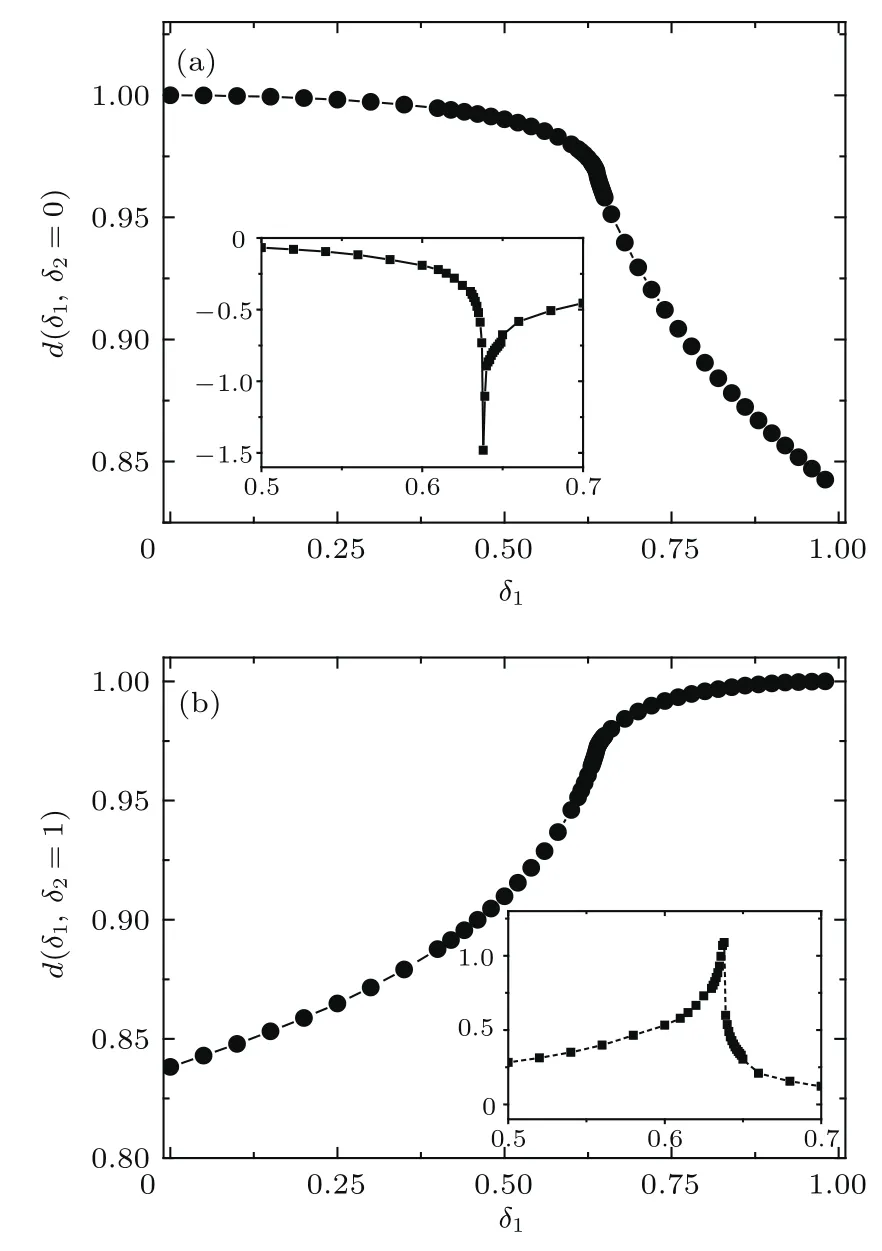
图2 χ =32时单位格点基态保真度d(δ1,δ2)随δ1的变化(内插图为单位格点基态保真度的一阶导数)(a) δ2=0;(b) δ2=1Fig.2.Ground sate fi delity per lattice site d(δ1,δ2)as a function of δ1for the truncation dimension χ =32:(a) δ2=0;(b) δ2=1.Insert:the fi rst derivation of the Ground state fi delity per lattice site d(δ1,δ2).

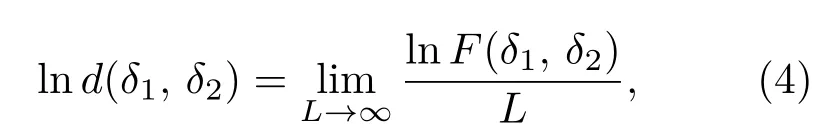
其中基态保真度F(δ1,δ2)就是两个不同基态和⟩间的相似程度,L表示系统的尺寸.

在图2(a)和图2(b)中,我们分别计算了截断维数χ=32时参考态选为δ2=0和δ2=1的单位格点基态保真度d(δ1,δ2).两个保真度数据都在δc=0.638时出现了剧烈的变化.为了能更准确地刻画结果,我们另外在内插图中给出了保真度的一阶导数.保真度一阶导数的奇异点δc=0.638就对应着系统的量子相变点,这个变化位置和前面von Neumann熵的奇异点的位置是相同的.其结果也表明单位格点量子基态保真度能够被用来刻画系统的量子相变.

4.3 序参量

为了更深刻地理解系统的量子相变,需要找到各个相中的序参量.对于含有局域序的二聚化相,其序参量就是近邻自旋关联的长程交替,即二聚化序OD,其表达式为

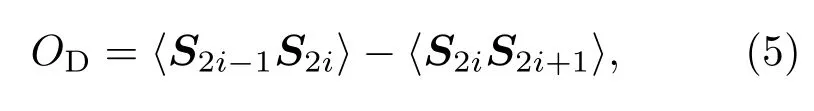
其中i和j是自旋格点的位置,则格点间的距离就是|i−j|.

在图3(a)中,基于(5)式算出了截断维数χ=32时以键交替参数δ为变量的二聚化序OD.数据表明,在整个参数变化范围内,系统中的二聚化序都是有限值.也就是说二聚化效应存在于整个参数变化范围.但是在相变点δc=0.638附近,序参量变化较剧烈.因此,我们在内插图中给出了二聚化序的一阶导数.从中可以看出二聚化序的一阶导数出现了一个峰,峰值的位置δ=0.638就是系统所对应的相变点.该结果也符合von Neumann熵和单位格点基态保真度的结论.

在图3(b)中,基于(6)式计算出了截断维数χ=32时以键交替参数δ为变量的Néel序ON.数据表明在δ<0.638的范围内,Néel序的值是有限的.当δ>0.638时,Néel序的值都为零.这一结果表明,当键交替参数δ改变时,Néel相存在于δ<0.638的范围内.当键交替参数δ增大到δc=0.638时,系统过渡到了局域序的二聚化相.以上结果说明了在标准的XXZ模型中加入了键交替效应后,当键交替强度达到δc时,系统中原有的长程拓扑行为就会被打破,从而过渡到局域的二聚化相.

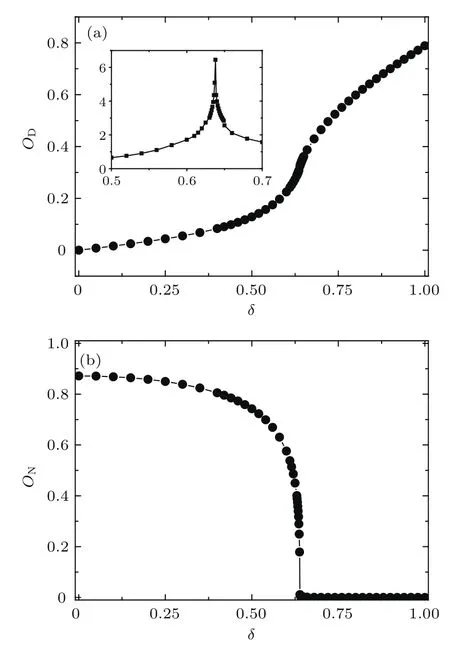
图3 截断维数χ=32时的序参量随δ的变化 (a)二聚化序OD(内插图为一阶导数);(b)Néel序ONFig.3.Order paremeters as a function of δ with the truncation dimension χ=32:(a)Dimer order parameter OD( fi rst derivation of ODin the insert);(b)Néel order parameter ON.

4.4 临界指数

对于低维的自旋系统而言,基于共形场理论的中心荷是一个描述量子相变性质的重要参数.因此,要研究相变的临界性质就必须计算出相变点的中心荷以描述相变的类型.相较于其他的数值方法,iMPS法可以方便且有效地计算出相变点的中心荷,从而得到相变所属的普适类.在iMPS法表示下,我们可以从相变点的von Neumann熵S和有限纠缠关联长度ξ对于不同截断维数χ的标度关系得到相变点的中心荷[26−28].其表达式为

以及

其中,c是共形场理论中的中心荷,κ是一个和有限纠缠相关的标度指数,有限纠缠关联长度ξ可以直接从iMPS表示的转移矩阵中计算得到.

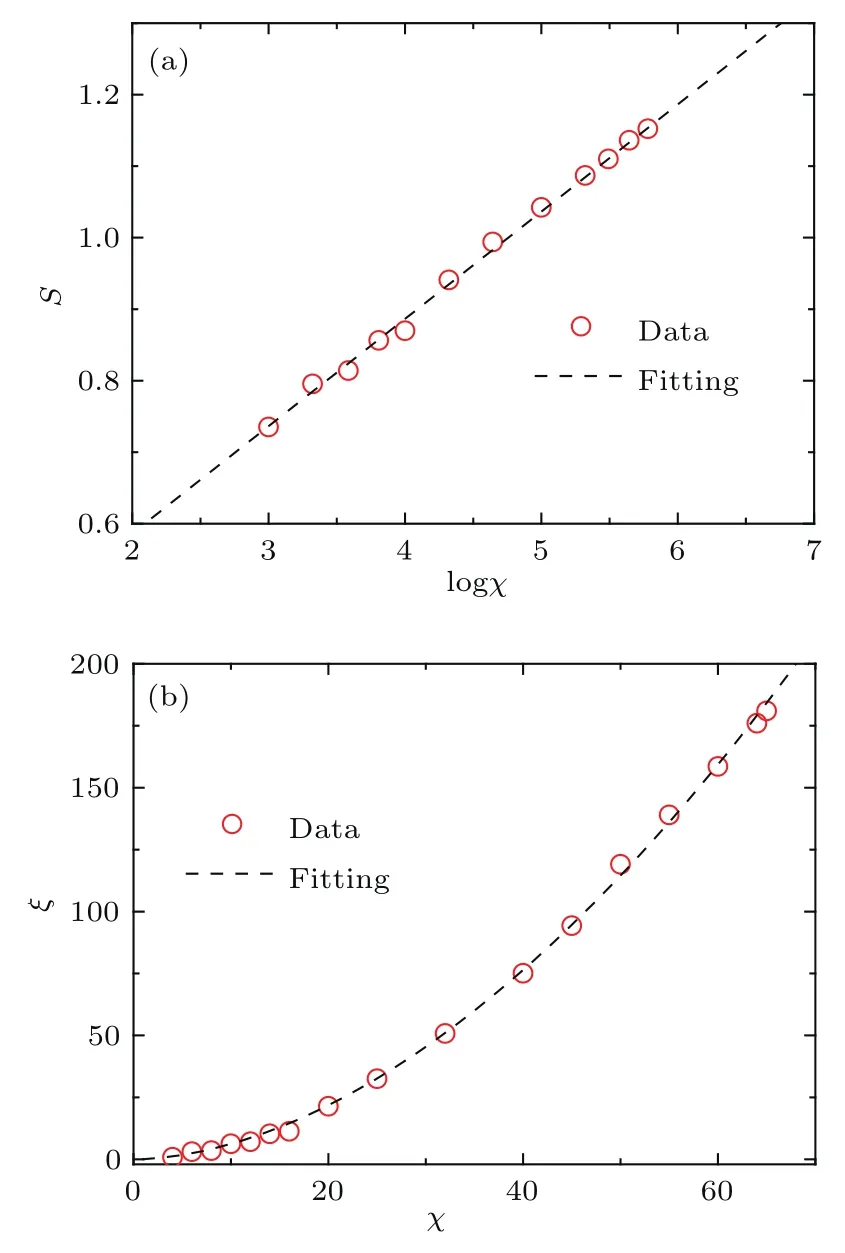
图4 相变点δc=0.638处的有限标度拟合 (a)von Neumann熵S拟合;(b)有限纠缠关联长度ξ拟合Fig.4.Finite scaling at the critical point δc=0.638:(a)Scaling of ground state von Neumann entropy S;(b)scaling of fi nite correlation length ξ.

为了研究此系统相变的所属类型,在图4中我们分别给出了在相变点δc=0.638处不同截断维数χ的von Neumann熵S(图4(a))和有限纠缠关联长度图4(b)),并对它们分别做了数值拟合.从图4可以看出,von Neumann熵S和有限纠缠关联长度ξ随着截断维数χ的增加是发散的.为了得到中心荷,我们选取数值拟合函数S=alogχ+b和ξ=Aχκ.对于von Neumann熵S的拟合所得到的拟合系数分别为a=0.150和b=0.286.对于有限纠缠关联长度ξ的幂律拟合所得到的拟合系数分别为A=0.096和κ=1.811.由上面的拟合系数a和κ可以计算出此相变的中心荷为c=0.497.我们所拟合出的中心荷的值非常接近于二维经典Ising普适类[10]的中心荷c=0.5.因此,此系统的相变属于共形场理论中的二维经典Ising普适类.

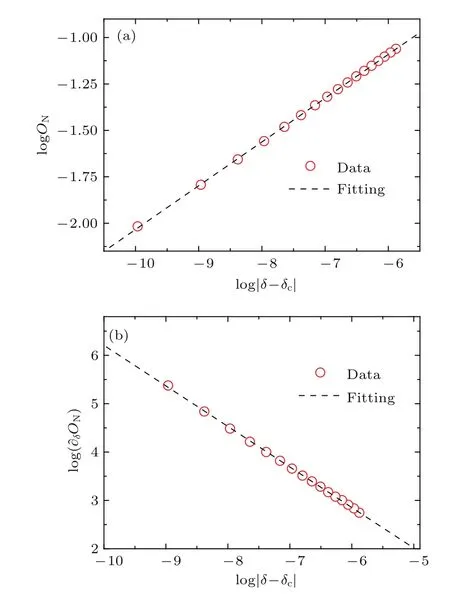
图5 临界指数β′和γ′的拟合 (a)β′;(b)γ′Fig.5.Critical exponents β′and γ′at the critical point:(a) β′;(b) γ′.

临界指数是研究系统临界性质的重要参数.近年来,人们也开发了不同的方法来刻画相变的临界指数.例如,在文献[20,21]中,作者利用量子重整化群方法分别计算了自旋1/2 XY模型和各向异性的铁磁海森伯模型的concurrence和negativity,从而基于它们在系统尺寸上的标度关系拟合出了相变相应的临界指数,从而揭示了相变的深层次物理性质.本文中,在拓扑有序相中,相变的某些临界指数是和非局域序联系在一起的.因此,为了更清楚地描述此系统相变的临界行为,在图5(a)中基于张量网络表示的iMPS方法计算出了在相变点δc=0.638附近非局域的Néel序ON随着|δ−δc|的变化.从图5(a)可以看出,非局域的Néel序ON和|δ− δc|有着幂律关系, 即ON∝ |δ− δc|β′, 其中β′就是一个相变的特征指数.图中选取的拟合函数为logON=β′log|δ−δc|+β′0.通过数值拟合,得到相变的特征指数β′=0.236,常数β′0=0.324. 另外,我们也发现Néel序ON的一阶导数随着|δ−δc|的增大是呈幂律衰减的,即∂ON/∂δ∝ |δ− δc|−γ′. 因此,图5(b)给出了Néel序的一阶导数∂ON/∂δ随着|δ−δc|的变化.同样拟合函数被选为log∂ON/∂δ=−γ′log|δ−δc|+γ′0.通过数值拟合,得到相变的特征指数γ′=0.838,常数γ′0=−2.176.以上基于iMPS表示方法所得到的临界指数对于量子自旋系统和相变的临界性质研究是具有指导意义的.

5 结 论

本文研究了含有键交替效应的一维反铁磁自旋为1的XXZ海森伯模型的量子相变.基于张量网络表示下的iMPS算法,分别计算了系统基态von Neumann熵、单位格点保真度和序参量.结果表明,在标准的一维反铁磁自旋为1的XXZ海森伯模型中加入键交替效应,整个键交替参数δ的变化范围内都存在局域的二聚化序.当键交替强度超过δc=0.638后,系统中原有的长程拓扑性质会被打破从而转变为二聚化相.利用iMPS方法,本文从相变点处的量子纠缠和有限关联长度的标度关系拟合出了相变的中心荷c≃0.5,得出此相变属于经典的二维Ising普适类.另外,我们发现Néel序及Néel的一阶导数在相变点附近是幂律变化的.通过对Néel序及Néel一阶导数的数值拟合,我们得到了相变点处的特征临界指数β′=0.236和γ′=0.838.我们基于iMPS表示方法所得到的临界指数对于量子自旋系统和相变的临界性质研究是具有指导意义的.

[1]Sachdev S 1999 Quantum Phase Transitions(Cambridge:Cambridge University Press)

[2]Kitazawa A,Nomura K,Okamoto K 1996 Phys.Rev.Lett.76 4038

[3]Rizzi M,Rossini D,Chiara G D,Montangero S,Fazio R 2005 Phys.Rev.Lett.95 240404

[4]Peters D,McCulloch I P,Selke W 2009 Phys.Rev.B 79 132406

[5]Katsura H,Tasaki H 2013 Phys.Rev.Lett.110 130405

[6]Kennedy T,Tasaki H 1992 Phys.Rev.B 45 304

[7]Hatsugai Y 2007 J.Phys.:Condens.Matter 19 145209

[8]Pollmann F,Berg E,Turner A,Oshikawa M 2012 Phys.Rev.B 85 075125

[9]Ueda H,Nakano H,Kusakabe K 2008 Phys.Rev.B 78 224402

[10]Su Y H,Cho S Y,Li B,Wang H,Zhou H 2012 J.Phys.Soc.Jpn.81 074003

[11]Vidal G 2007 Phys.Rev.Lett.98 070201

[12]Su Y H,Hu B,Li S,Cho S Y 2013 Phys.Rev.E 88 032110

[13]Wang H,Li B,Cho S Y 2013 Phys.Rev.B 87 054402

[14]Wang H,Cho S Y 2015 J.Phys.:Condens.Matter 27 015603

[15]Kato Y,Tanaka A 1994 J.Phys.Soc.Jpn.63 1277

[16]Osterloh A,Amico L,Falci G,Fazio R 2002 Nature 416 608

[17]Korepin V E 2004 Phys.Rev.Lett.92 096402

[18]Amico L,Fazio R,Osterloh A,Vedral V 2008 Rev.Mod.Phys.80 517

[19]Chung M,Landau D P 2011 Phys.Rev.B 83 113104

[20]Ma F,Liu S,Kong X 2011 Phys.Rev.A 83 062309

[21]Xu Y,Wang L,Kong X 2013 Phys.Rev.A 87 012312

[22]Zanardi P,PaunkoviN 2006 Phys.Rev.E 74 031123

[23]Rams M M,Damski B 2011 Phys.Rev.Lett.106 055701

[24]Zhou H,BarjaktareviJ P 2008 J.Phys.A:Math.Theor.41 412001

[25]Yu Y,Müller G,Viswanath V S 1996 Phys.Rev.B 54 9242

[26]Tagliacozzo L,de Oliveira T R,Iblisdir S,Latorre J I 2008 Phys.Rev.B 78 024410

[27]Pollmann F,Mukerjee S,Turner A,Moore J E 2009 Phys.Rev.Lett.102 255701

[28]Su Y H,Chen A M,Xiang C,Wang H,Xia C,Wang J 2016 J.Stat.Mech.2016 123102

PACS:03.67.–a,03.65.Ud,03.67.HkDOI:10.7498/aps.66.120301

Quantum entanglement and critical exponents in one-dimensional spin-1 bond-alternating XXZ chains∗

Su Yao-Heng1)Chen Ai-Min1)2)Wang Hong-Lei3)Xiang Chun-Huan4)†

1)(School of Science,Xi’an Polytechnic University,Xi’an 710048,China)
2)(School of Science,Xi’an Jiaotong University,Xi’an 710049,China)
3)(College of Medical Informatics,Chongqing Medical University,Chongqing 400016,China)
4)(School of Public Health and Management,Chongqing Medical University,Chongqing 400016,China)

3 January 2017;revised manuscript

28 March 2017)

The characterization of the quantum phase transition in a lowdimensional system has attracted a considerable amount of attention in quantum manybody systems.As one of the fundamental models in quantum magnetism,spin-1 models have richer phase diagrams and show more complex physical phenomena.In the spin-1 antiferromagnetic XXZ model,the Haldane phase and the Néel phase are the gapped topologic phases which cannot be characterized by the local order parameters.To characterize the nature in such phases,one has to calculate the non-local long range order parameters.

Normally,the non-local order parameter in the topological phase is obtained from the extrapolation of fi nite-sized system in numerical study.However,it is difficult to extract the critical exponents with such an extrapolated non-local order parameter due to the numerical accuracy.In a recently developed tensor network representation,i.e.,the in fi nite matrix product state(iMPS)algorithm,it was shown that the non-local order can be directly calculated from a very large lattice distance in an in fi nite-sized system rather than an extrapolated order parameter in a fi nite-sized system.Therefore,it is worthwhile using this convenient technique to study the non-local orders in the topological phases and characterize the quantum criticalities in the topological quantum phase transitions.

In this paper,by utilizing the in fi nite matrix product state algorithm based on the tensor network representation and in fi nite time evolving block decimation method,the quantum entanglement, fi delity,and critical exponents of the topological phase transition are investigated in the one-dimensional in fi nite spin-1 bond-alternating XXZ Heisenberg model.It is found that there is always a local dimerization order existing in the whole parameter range when the bond-alternative strength parameter changes from 0 to 1.Also,due to the e ff ect of the bond-alternating,there appears a quantum phase transition from the long-rang ordering topological Néel phase to the local ordering dimerization phase.The von Neumann entropy, fi delity per lattice site,and order parameters all give the same phase transition point at δc=0.638.

To identify the type of quantum phase transition,the central charge c≃0.5 is extracted from the ground state von Neumann entropy and the fi nite correlation length,which indicates that the phase transition belongs to the twodimensional Ising universality class.Furthermore,it is found that the Néel order and the susceptibility of Néel order have power-law relations to|δ− δc|.From the numerical fi tting of the Néel order and its susceptibility,we obtain the characteristic critical exponents β′=0.236 and γ′=0.838.It indicates that such critical exponents from our method characterize the nature of the quantum phase transition.Our critical exponents from the iMPS method can provide guidance for studying the properties of the phase transition in quantum spin systems.

quantum phase transition,quantum entanglement,topological phase,critical exponent

10.7498/aps.66.120301

∗国家自然科学基金(批准号:11504283)资助的课题.

†通信作者.E-mail:wanghl@cqmu.edu.cn

©2017中国物理学会Chinese Physical Society

http://wulixb.iphy.ac.cn

*Project supported by the National Natural Science Foundation of China(Grant No.11504283).

†Corresponding author.E-mail:wanghl@cqmu.edu.cn