有限温度下一维Hubbard模型的化学势泛函理论研究∗
2017-08-07陆展鹏魏兴波刘天帅陈阿海高先龙
陆展鹏 魏兴波 刘天帅 陈阿海 高先龙
(浙江师范大学物理系,金华 321004)
有限温度下一维Hubbard模型的化学势泛函理论研究∗
陆展鹏 魏兴波 刘天帅 陈阿海 高先龙†
(浙江师范大学物理系,金华 321004)
(2017年1月7日收到;2017年3月26日收到修改稿)
通过数值方法求解了有限温度下一维均匀Hubbard模型的热力学Bethe-ansatz方程组,得到了在给定温度和相互作用强度情况下,比热c、磁化率χ和压缩比κ随化学势µ的变化图像.基于有限温度下一维均匀Hubbard模型的精确解,利用化学势(µ)-泛函理论研究了一维谐振势下的非均匀Hubbard模型,给出了金属态和Mott绝缘态下不同温度情况时局域粒子密度ni和局域压缩比κi随格点的变化情况.
热力学Bethe-ansatz方程组,压缩比,Hubbard模型,化学势泛函理论
1 引言
20世纪初,玻色和爱因斯坦提出了著名的玻色-爱因斯坦凝聚(Bose-Einstein condensation,BEC)理论,他们预言,对于玻色气体,当温度低于某一个临界值Tc时,所有的粒子将会占据能量最低的量子态[1].随着1985年美国华裔科学家朱棣文等[2]利用激光冷却技术获得了接近绝对零度的温度,冷原子物理开始成为研究的热点.之后在1995年,Ketterle,Cornell和Wiemann首次在实验中实现了Na和Rb的BEC凝聚体[3,4].而后人们开始设法冷却费米气体并得到费米凝聚体.由于费米气体受到泡利不相容原理的限制,所以冷却难度比玻色气体更大.在1999年,Jin的研究组[5]实现了费米凝聚.随着Feshbach共振技术的发展,人们可以通过磁场改变束缚态原子的散射长度,进而调节原子之间的相互作用,从而大大推动了冷原子实验的发展[6,7].另外由于光晶格技术的发展,人们在冷原子体系中可以构造出非常干净的一、二、三维晶格结构[8].
一维体系呈现出丰富的物理性质,如20世纪,Tomonaga[9]和Luttinger[10]提出的著名的Luttinger液体理论.他们指出一维费米体系之中,如果考虑相互作用,则朗道液体理论不再适用,体系中只有集体激发,没有单粒子激发,其中最明显的特征即自旋电荷分离[11].很多一维多粒子体系具有精确可解性,如1931年Bethe[12]提出的Bethe-ansatz理论,可求解一维Heisenberg模型;1963年,Lieb和Liniger[13]求解了一维玻色气体;1967年,Yang[14]和Gaudin[15]求解了自旋为1/2的费米气体;1968年,Lieb和Wu[16]求解了一维Hubbard模型.以上理论结果可以与一维冷原子实验相互印证,并用于理解一维谐振势受限体系中呼吸模的集体激发情况[17]和自旋电荷分离现象[18,19]等.
由于绝对零度无法达到,考虑到温度对受限体系的影响具有十分现实的意义,所以本文研究一维有限温度的晶格冷原子晶格体系.在1969年,杨振宁等[20]提出了研究一维可积模型的热力学Bethe-ansatz(TBA)方法,随后,日本物理学家Takahashi[21,22]研究了XXX链模型和具有排除相互作用的自旋−1/2模型的热力学性质.此后,一维有限温度的研究成为热点,如利用TBA方程组结合Haldane统计讨论低温下一维强相互作用任意子简并特征[23]和能态性质[24],研究有限温度下吸引相互作用的费米气体的配对特征和相变性质[25,26],有限温下自旋为1的玻色子在一维谐振势中的量子临界现象[19,27],以及有限温度下一维吸引相互作用的费米气的Tomonaga-Luttinger液体相变[19,28]等.
由于冷原子实验中的体系普遍是非均匀的,体系一般变得不可精确求解.利用一维均匀体系的精确解并结合局域密度近似的密度泛函理论求解一维非均匀体系,是一种可行的方法[29−32].利用此密度泛函理论可以研究有限温度下一维晶格体系的交换关联势[29],有限温度下一维谐振势Hubbard模型的磁导率等热力学量[33],以及用含时密度泛函理论研究一维费米体系自旋电荷分离[34,35]等性质.
基于以上的研究,我们数值求解了有限温度下一维均匀Hubbard模型的TBA方程组[36],主要分析了在不同相互作用和不同温度下,磁化率χ、比热c和压缩率κ等热力学量,之后基于这些一维均匀体系的性质,以化学势为泛函结合密度泛函理论[37]方法研究了一维非均匀Hubbard模型,得到了不同温度下金属相和Mott绝缘相的粒子密度和局域压缩比随格点的变化情况.研究结果表明,在低温情况下,一维均匀体系中的磁化率χ、比热c和压缩率κ能够度量四个相变区域,分别为真空态、金属态、Mott绝缘态和带绝缘态.随着温度的升高,体系热涨落逐渐占据主导地位,取代量子涨落成为主导,Mott绝缘体相会消失.在非均匀体系中,体系处于不同相的共存相.随着温度的升高,热涨落会破坏势阱中间的Mott绝缘相,相应的粒子密度分布ni和局域压缩比κi的变化反映了这一过程.
2 理论模型
本文先讨论一维均匀Hubbard模型,其哈密顿量的形式如下:

式中,t为近邻格点的跳跃能;U为同格点粒子之间的相互作用,本文只研究U>0的排斥相互作用情况;µ为化学势;h为磁场;为i格点自旋为σ的产生算符,表示为i+1格点自旋为σ的湮灭算符;为粒子数算符.
比热c、磁化率χ和压缩比κ的表达式如下:

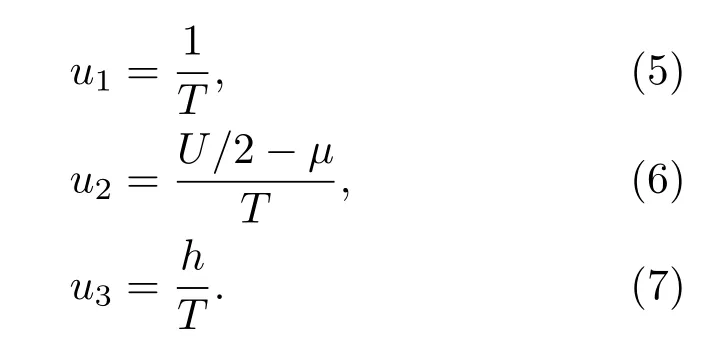
热力学势g所满足的TBA耦合方程的具体表达式及其相关的二阶微分量的求解过程可以参考文献[36].
我们首先通过数值方法求解一维均匀Hubbard模型的TBA耦合方程组,得到磁化率χ、比热c、压缩率κ、化学势µ、粒子密度分布n等热力学量,通过分析这些物理量了解系统的量子相变.基于对这些热力学量的分析,我们研究一维受限谐振势下的Hubbard模型,

式中,Vext为外势强度,Na为总格点数.
对于一维非均匀Hubbard模型的求解,可以利用一维晶格密度泛函理论,即通过构造建立在Bethe-ansatz严格解基础上的交换关联势,用基于局域密度近似来求体系的定态或动力学性质(BALDA方法[11,17,29,33,34])来研究.但是上述方法在处理具有Mott绝缘相的情况时,由于此时构造的交换关联势在n=1的半充满情况下具有不连续性(即所谓的Mott能隙),此时基于BALDA的Kohn-Sham方程在不连续的交换关联势上下振荡,很难收敛,从而产生不能自洽求解的问题[37].考虑到密度和化学势之间具有一一对应的函数关系,基于密度的泛函理论等价于基于化学势(µ)的泛函理论,相应的BALDA变成µ-BALDA,以化学势为泛函的交换关联势是连续的,于是上述困难可以解决.
下面我们具体阐述µ-BALDA方法,讨论如何通过一维均匀体系的化学势µ(U,n)作为泛函,构造出非均匀体系的有效势Veff,并利用Kohn-Sham方程求解出非均匀体系的局域粒子密度ni.
我们先构造出均匀体系的交换关联势Vhxc[n],
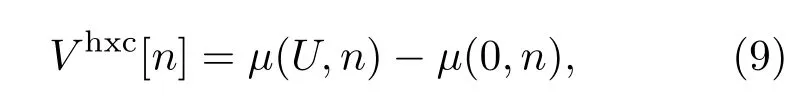
其中µ(U,n)代表均匀体系的化学势(以下简记为µ),µ(0,n)为均匀体系中U=0时的化学势,即动能.µ(U,n)可以通过如下公式求出:

式中e(U,n)是均匀体系中单位格点的能量.考虑到(10)式中的粒子密度和化学势具有一一对应的函数关系,n可以被反解出来,表示成以化学势µ为自变量的函数,

于是方程(9)中的交换关联势Vhxc[n]就可以表示成以化学势µ为泛函的函数Vhxc[µ],
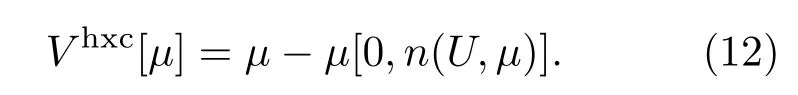
基于密度泛函理论,多粒子体系的薛定谔方程等价于一个在有效势场中的单粒子Kohn-Sham(KS)方程,
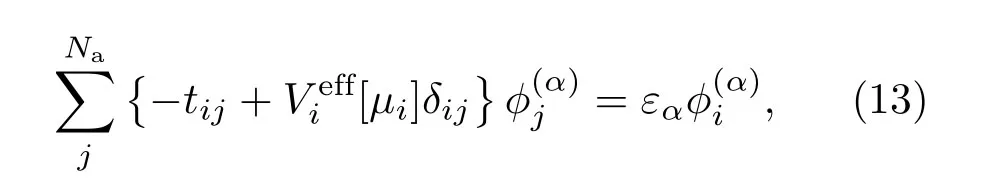
这里tij=t(当j=i±1)而其他情况下为0,其中系统的密度分布是由KS方程的轨道波函数自洽给出,
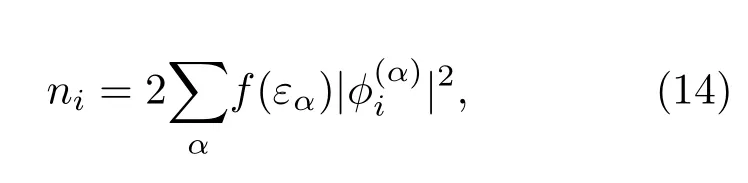
式中的α为能级指标,2来自于自旋简并,f(ω)={1+exp[β(ω−µ)]}−1是费米分布,β =1/(kBT)是温度的倒数,其中kB是玻尔兹曼常量.在实际计算中,非均匀体系的可由均匀系统的Vhxc[µ]在局域密度近似下给出:
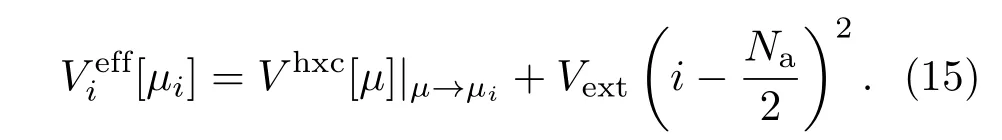
从方程(13)和(14)中计算密度分布等价于寻找以化学势为泛函的不动点问题:
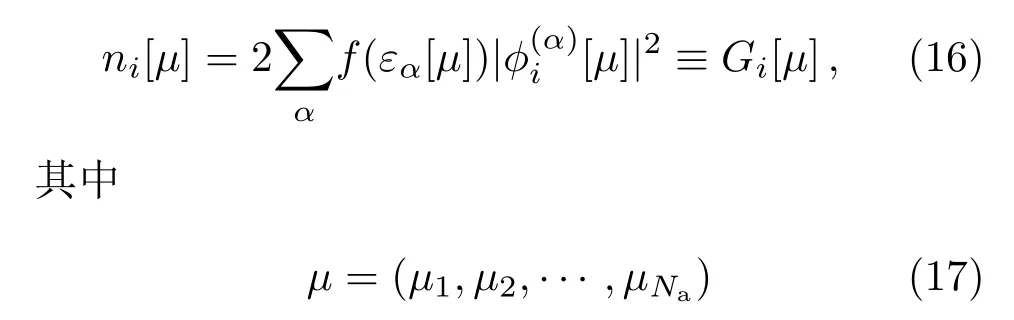
如前所述,对这些方程的普通迭代求解办法不能解决由于交换关联势不连续带来的不收敛问题.而更精妙的迭代方法如Newton-Rhapson方法也不能解决该问题,因为它用到了非线性方程对于未知变量的一级导数,其在不连续处会趋于无穷,同样会导致耦合方程的不收敛问题.这里我们拟用多维二分法来解决上述以化学势为泛函的不动点问题,即通过构造
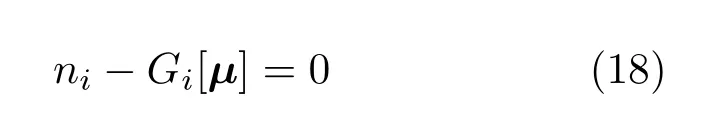
来找方程左边的函数与横轴的交点,即其零解,详细的数值解法参见文献[29].
3 结果分析与讨论
3.1 一维均匀Hubbard模型
本节先给出一维均匀Hubbard模型中比热c、磁化率χ和压缩比κ在不同温度和相互作用强度下的结果,分析这些物理量在度量量子相变中的作用.图1给出了低温(T=0.1)情况、不同相互作用强度U下的比热c、磁化率χ和压缩比κ随化学势µ变化的性质.
图1中比热c和压缩比χ的图像中均出现了四个峰值点或拐点,这四个峰值点分别对应着系统的四次相变:真空态向金属态转变,金属态向Mott绝缘体态转变,Mott绝缘体态向金属态转变,金属态向带绝缘体态转变.从压缩比κ的图像看出,当相互作用U不断增加时,压缩比κ中间出现了为零的区域,这部分区域对应Mott绝缘体相(绝缘相不可压缩),区域的大小也反映了Mott能隙的大小,随着相互作用U的增大,Mott绝缘体区域的范围也在增大.
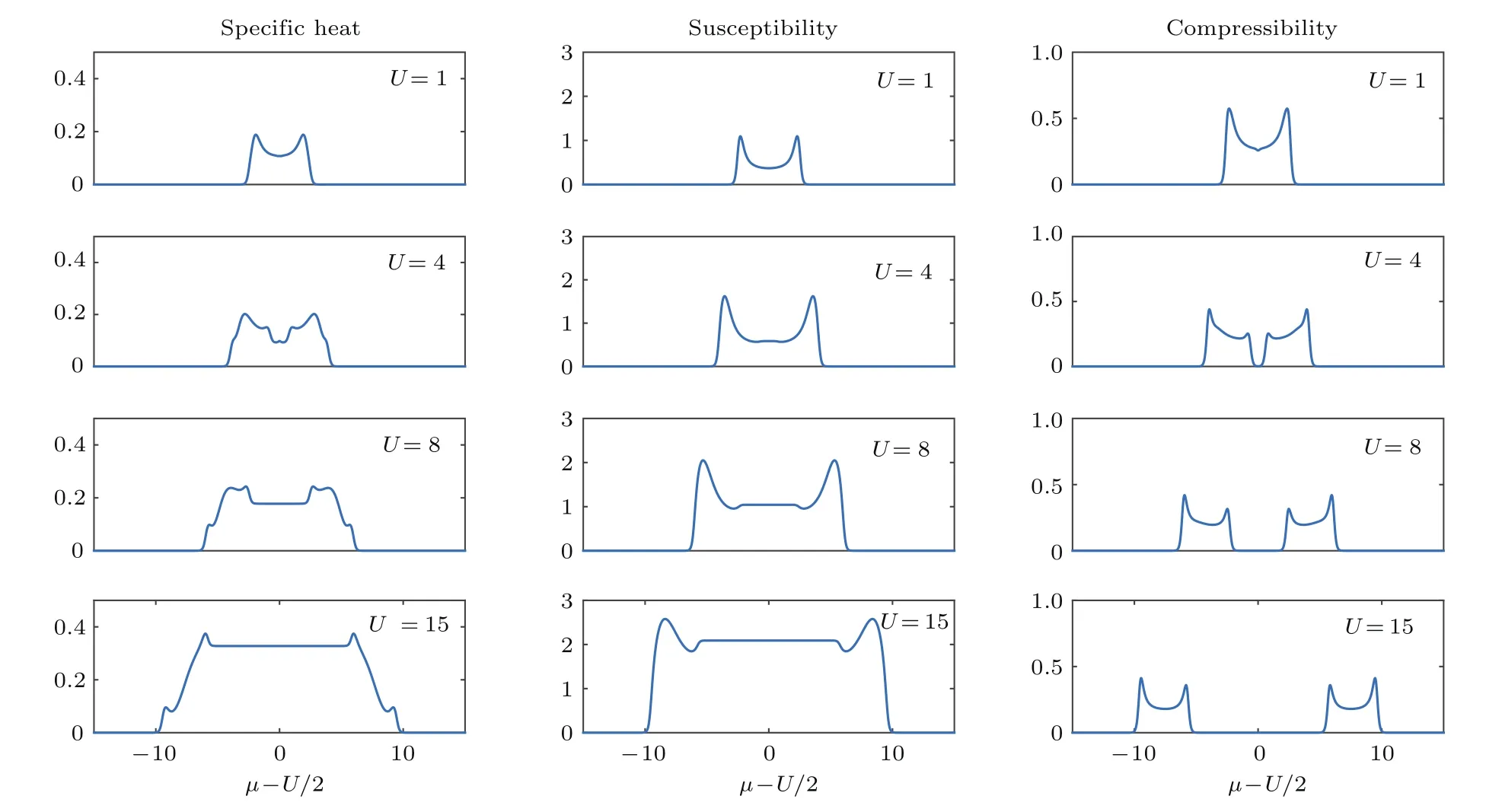
图1 (网刊彩色)温度T=0.1,不同相互作用强度(U=1,4,8,15)下的压缩比κ、比热c和磁化率χ随化学势µ的变化情况,其中对化学势进行了平移µ−U/2,使系统具有中心对称(数值计算方便取t=kB=1)Fig.1.(color online)Speci fi c heat c,susceptibility χ,and compressibility κ as a function of the chemical potentialµfor temperature T=0.1 and di ff erent interaction strength(U=1,4,8,15).In order to have the system of the central symmetry,we shift the chemical potentialµby U/2(for convenience,we let t=kB=1).
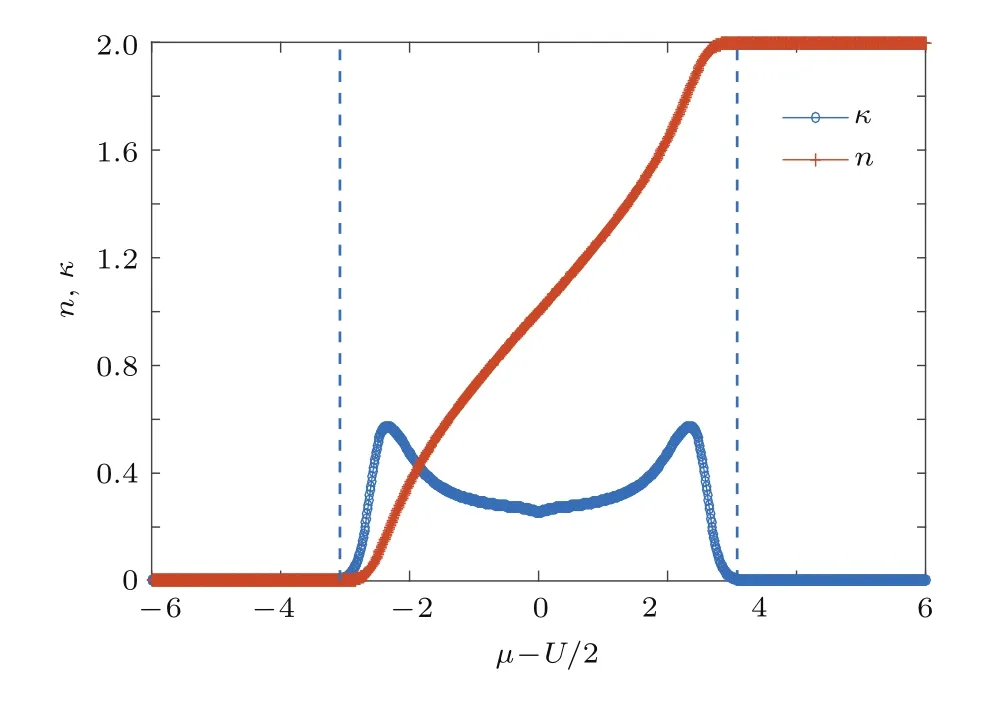
图2 (网刊彩色)T=0.1,U=1时压缩比κ和粒子密度n随µ的变化(图中的虚线从左到右把系统划分为真空区、金属相和带绝缘体相)Fig.2.(color online)Compressibility κ and density n as a function of the chemical potentialµfor temperature T=0.1 and interaction strength U=1.The dotted lines from left to right divide the system into the vacuum phase,the metal phase,and the bandinsulating phase.

图3 (网刊彩色)T=0.1,U=4压缩比时κ和粒子密度n随µ的变化(图中的虚线从左到右把系统划分为真空区、金属相、Mott绝缘体相、金属相和带绝缘体相)Fig.3.(color online)For the temperature T=0.1 and interaction strength U=4,compressibility κ,and density n as a function of the chemical potentialµ.The dotted line from left to right divide the system into the vacuum phase,the metal phase,the Mott-insulating phase,the metal phase,and the bandinsulating phase.
为了清晰地看出Mott绝缘相的区域,我们将不同相互作用U下压缩比κ和粒子密度n的结果放在一起比较,结果见图2、图3和图4.从图2可以看出,在低温(T=0.1)下,相互作用U较弱时,此时并非Mott绝缘体相(这与零温时有限相互作用在半充满情况下即为Mott绝缘相不同).此时压缩比κ的图像中没有反映出不可压缩的区域,而粒子密度n的图像上也没有出现n=1的半充满的Mott平台.从图3可以看出,由于粒子之间的相互作用U增强到4,压缩比κ的图像中间出现为零的不可压缩的Mott绝缘区域,而对应的粒子密度n也出现了n=1的半充满的Mott平台(图中的中间两条虚线部分对应的是Mott绝缘体系区域的范围).从图4可以看出,随着粒子之间的相互作用U增强到8,压缩比κ的图像中Mott绝缘体系区域的范围扩大了,而对应的粒子密度n的图像中的Mott平台也相应地增大,两者的变化是一致的.由此说明压缩比κ可以分辨各个量子相.如果将图1中的磁化率χ和比热c的结果和粒子密度n相比较也能够得出上述类似的结论.
图5给出了高温情况(T=1)、不同相互作用(U=1,4,8,15)下的压缩比κ、比热c和磁化率χ随化学势µ变化的结果.
从图5中我们发现热力学涨落破坏了原来的相变,四个相变点已经基本消失.在非常强的相互作用(U=15)下,Mott绝缘体区域仍然稳健,这可以从压缩比κ的图像中看出,其不可压缩的κ为零的区域依然存在,此时热力学涨落仍然没有破坏Mott绝缘体相.从上面的结果中我们发现低温下热力学量压缩比κ、比热c和磁化率χ可以清晰地反映出一维均匀Hubbard模型的相变情况,拐点和峰值点可以反映体系的相变.随着温度升高,热涨落会产生影响并很快破坏Mott绝缘相,但如果相互作用足够大,Mott绝缘体区域在高温(T=1.0)时仍然稳健.更详细的相图可由Bethe-ansatz解析解分析得到,具体可见文献[19,26,27].
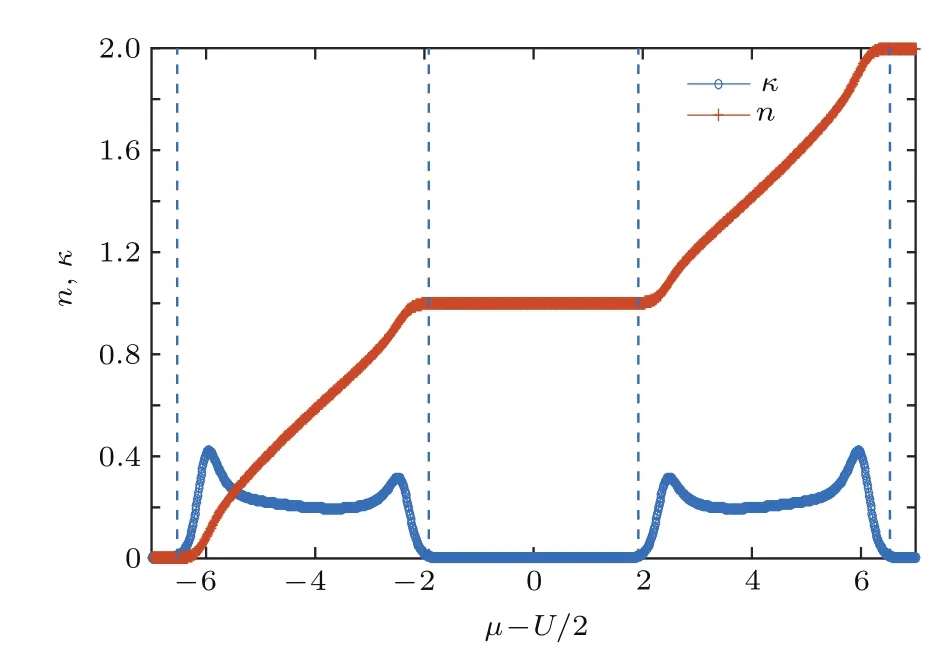
图4 (网刊彩色)T=0.1,U=8压缩比时κ和粒子密度n随µ的变化(图中的虚线从左到右把系统划分为真空区、金属相、Mott绝缘体相、金属相和带绝缘体相)Fig.4.(color line)Compressibility κ and density n as a function of the chemical potentialµfor temperature T=0.1 and interaction strength U=8.The dotted lines from left to right divide the system into the vacuum phase,the metal phase,the Mott-insulating phase,the metal phase,and the band-insulating phase.
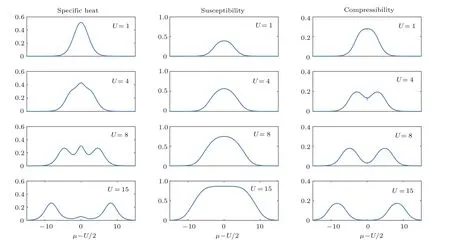
图5 (网刊彩色)温度T=1.0,不同相互作用强度(U=1,4,8,15)下的压缩比κ、比热c和磁化率χ随化学势µ的变化Fig.5.(color online)Speci fi c heat c,susceptibility χ,and compressibility κ as a function of the chemical potentialµfor temperature T=0.1 and di ff erent interaction strength(U=1,4,8,15).
3.2 一维束缚势中的Hubbard模型
本节分析光晶格中的一维费米冷原子体系,由于束缚势的存在,体系变成非均匀的.在单带近似和紧束缚模型下,体系可由非均匀的Hubbard模型[方程(8)]描写.下面我们讨论金属相和Mott绝缘相中的局域粒子密度ni和局域压缩比κi在不同温度下的分布.
图6是相互作用U=8,粒子数N=30时,不同温度(T=0.01,0.1,0.6,1.0)下金属态局域粒子密度ni随格点i的变化.其他物理参数为:晶格长度Na=200,谐振势强度Vext=2.5×10−3,这些参数也用在了以下其他图的计算中.

图6 (网刊彩色)相互作用U=8,粒子数N=30时,不同温度T=0.01,0.1,0.6,1.0下金属态的局域粒子密度ni随着格点i的变化Fig.6.(color online)The local density niof the metal phase as a function of the lattice site i for interaction strength U=8,the number of particles N=30,and di ff erent temperature T=0.01,0.1,0.6,1.0.
从图6可以看出,温度较低(T=0.01)时,量子涨落引起的Friedel振荡仍然可见,随着温度的升高,热力学涨落占据主导作用,Friedel振荡不复存在,密度分布呈高斯型.
图7为相互作用U=8,粒子数N=70时,不同温度(T=0.01,0.1,0.6,1.0)下Mott绝缘态局域粒子密度ni的分布情况,从图7可以看出,在温度比较低的情况下,整个体系是金属相和Mott绝缘相共存,Mott平台(ni=1)存在于势阱中部,两边属于金属相.温度T从0.01升高至0.1时,Mott绝缘相整体保持稳定,逐渐从Mott平台的两边开始受到破坏.分析表明,Mott平台稳健存在于T<0.3,破坏Mott相的温度和均匀体系相近.当温度T升高到1.0时,热力学涨落占主导作用,体系的密度分布接近于高斯型.
为了更好地刻画温度和相互作用对Mott绝缘相的影响,我们计算了局域压缩比,定义为κi= κ(n)|n→ni.图8为温度T=0.1,相互作用U=8时,局域粒子密度分布ni和局域压缩比κi的对比图.从图8可以看出,体系的局域压缩比κi为零的不可压缩区域对应着Mott绝缘平台(虚线分割的中间部分正好对应Mott绝缘区)和真空态,分别对应着密度分布ni=1和ni=0.图9为高温情况T=1.0的局域压缩比κi和局域粒子密度ni的对比,可以看出局域压缩比在中间区域有下降的趋势但不为零,这正说明了随着温度的升高,由于相互作用和束缚势产生的Mott绝缘平台被破坏,体系重新变成了可压缩的金属相,相应的密度为ni<1.

图7 (网刊彩色)相互作用U=8,粒子数N=70时,不同温度T=0.01,0.1,0.6,1.0下金属相和Mott绝缘相共存时的局域粒子密度ni随着格点i的变化Fig.7.(color online)The local density niof the metal-Mott insulating mixed phase as a function of the lattice site i for interaction strength U=8,the number of particles N=70,and di ff erent temperature T=0.01,0.1,0.6,1.0.

图8 (网刊彩色)温度T=0.1,相互作用U=8,粒子数N=70时,局域粒子密度ni和局域压缩比κi随着格点i的变化 (图中的虚线从左到右把系统划分为真空态、金属相、Mott绝缘体相、金属相、真空态)Fig.8.(color online)The local density niand local compressibility κias a function of the lattice site i for temperature T=0.1,interaction strength U=8,and the number of particles N=70.The dotted line from left to right divide the system into the vacuum phase,the metal phase,the Mott-insulating phase,the metal phase,and the vacuum phase.
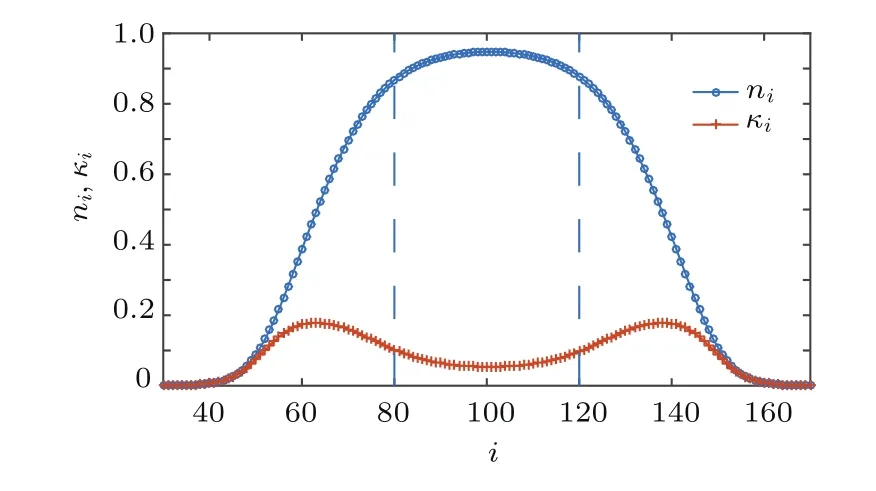
图9 (网刊彩色)温度T=1.0,相互作用U=8,粒子数N=70时,局域粒子密度ni和局域压缩比κi随着格点i的变化Fig.9.(color online)The local density niand the local compressibility κias a function of the lattice site i for temperature T=1.0,interaction strength U=8,and the number of particles N=70.
为了更好地理解有限温度下金属相向Mott绝缘相的转变过程,我们给出了一维束缚势中的Hubbard模型在给定粒子数N=70、晶格长度Na=200和谐振势强度Vext=2.5×10−3下的T-U相图,如图10所示.
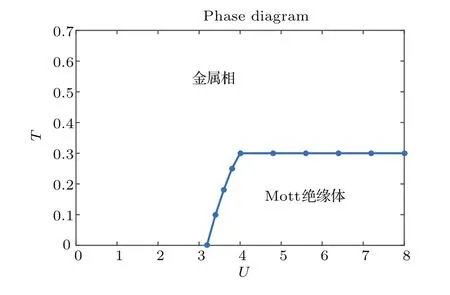
图10 (网刊彩色)一维束缚势中的Hubbard模型在给定粒子数N=70、晶格长度Na=200和谐振势强度Vext=2.5× 10−3下的温度-相互作用(T-U)相图(图中横坐标表示相互作用U,纵坐标表示温度T,图中的点是两个相的分界点)Fig.10.(color online)T-U phase Diagram of a harmonically trapped Hubbard model in one dimension with the number of particles N=70,the length of the lattice Na=200 and the harmonic potential strength Vext=2.5×10−3.The points in the divide the region into two quantum phases.
从图10中我们可以看出,Mott绝缘相只存在于温度T 6 0.3和相互作用U>3.2的区域,随着温度的升高,体系的Mott绝缘相会被破坏掉.
4 总 结
本文通过数值方法求解了一维均匀Hubbard模型的TBA方程组,得到了不同温度和相互作用下压缩比κ、比热c和磁化率χ等热力学量.发现在低温下,这三个热力学量(特别是压缩比κ)能够清晰地反映出体系的四个相变,分别对应着体系从真空态向金属态转变、金属态向Mott绝缘体态转变、Mott绝缘体态向金属态转变、金属态向带绝缘体态转变.随着温度的升高,热涨落逐渐取代量子涨落成为主导,温度会破坏掉原有体系的Mott绝缘体相,明显的相变点消失.而后利用一维均匀Hubbard模型的Bethe-ansatz严格解的数值结果,我们构造了可以用于研究一维非均匀Hubbard模型的化学势泛函方法:µ-BALDA,该方法从理论上讲是严格的密度泛函理论的变种.化学势泛函理论的构造解决了密度泛函理论中Kohn-Sham耦合方程在交换关联势不连续时的不收敛问题,并把问题转变成用多维二分法来解决以化学势为泛函的不动点问题,从而收敛性可以得到保障.
我们用µ-BALDA方法我们数值求解了有限温度下一维谐振势中的Hubbard模型,得到了不同温度下粒子的密度分布情况.从结果中可以看出在给定相互作用U的情况下,逐渐升高温度,热涨落会破坏金属态中的Friedel振荡和Mott绝缘体平台,最终变成平滑的高斯分布.而Mott绝缘体在一定温度范围内保持稳定,平台的破坏是从边界开始到中心地带,从而使整个Mott平台被破坏.最后通过对比非均匀体系的局域压缩比κi,并与粒子密度分布ni进行了对比,验证了温度对Mott绝缘态的破坏.在给定粒子数、晶格长度和谐振势强度下,我们给出了一个简单的T-U相图.由相图可知在此情况下Mott绝缘相只存在于温度T 6 0.3和相互作用U>3.2的区域内.
本文所运用的µ-BALDA方法可以进一步推广到非均匀的具有短程相互作用的Gaudin-Yang模型和吸引Hubbard模型中去,其中自旋激发有能隙,相应的交换关联势在自旋为零处不连续.另外也可以推广到一维XXZ模型 (可用Jordan-Wigner变换变成一维近邻相互作用的极化费米子模型,在Tomonaga-Luttinger液体相和公度的电荷密度波相的临界点处n=0.5,交换关联势不连续)[38]中去,或推广到有限温度(或多组分)的上述模型[26]中去.
感谢浙江师范大学物理系王沛副教授在论文构思阶段部分物理内容的讨论.
参考文献
[1]Wang Z C 2003 Thermodynamics Statistical Physics(Beijing:Higher Education Press)p300(in Chinese)[汪志诚1993 热力学和统计物理学(北京:高等教育出版社)第300页]
[2]Chu S,Hollberg L,Bjorkholm J E,Cable A,Ashkin A 1985 Phys.Rev.Lett.55 48
[3]Davis K B,Mewes M O,Andrews M R,van Druten N J,Durfee D S,Kurn D M,Ketterle W 1995 Phys.Rev.Lett.75 3969
[4]Anderson M H,Ensher J R,Matthews M R,Wieman C E,Cornell E A 1995 Science 269 198
[5]DeMarco B,Jin D S 1999 Science 285 1703
[6]Feshbach H 1958 Ann.Phys.5 357
[7]Batchelor M T,Bortz M,Guan X W,Oelkers N 2005 Phys.Rev.A 72 061603
[8]Pachos J K,Knight P L 2003 Phys.Rev.Lett.91 107902
[9]Tomonaga S 1950 Prog.Theo.Phys.5 544
[10]Luttinger J M 1963 J.Math.Phys.4 1154
[11]Gao X L 2010 Phys.Rev.B 81 104306
[12]Bethe H 1931 Z.Phys.71 205
[13]Lieb E H,Liniger W 1963 Phys.Rev.130 1605
[14]Yang C N 1967 Phys.Rev.Lett.19 1312
[15]Gaudin M 1967 Phys.Lett.A 24 55
[16]Lieb E H,Wu F Y 1968 Phys.Rev.Lett.20 1445
[17]Hu H,Gao X L,Liu X J 2014 Phys.Rev.A 90 013622
[18]Lee J Y,Guan X W,Sakai K,Batchelor M T 2012 Phys.Rev.B 85 085414
[19]Guan X W,Batchelor M T,Lee C 2013 Rev.Mod.Phys.85 1633
[20]Yang C N,Yang C P 1969 J.Math.Phys.10 1115
[21]Takahashi M 1969 Prog.Theo.Phys.42 1098
[22]Takahashi M 1972 Prog.Theo.Phys.47 69
[23]Batchelor M T,Guan X W 2006 Phys.Rev.B 74 195121
[24]Batchelor M T,Guan X W,Oelkers N 2006 Phys.Rev.Lett.96 210402
[25]Guan X W,Batchelor M T,Lee C,Bortz M 2007 Phys.Rev.B 76 085120
[26]Jiang Y Z,Chen Y Y,Guan X W 2015 Chin.Phys.B 24 050311
[27]Kuhn C C N,Guan X W,Foerster A,Batchelor M T 2012 Phys.Rev.A 86 011605
[28]Guan X W,Lee J Y,Batchelor M T,Yin X G,Chen S 2010 Phys.Rev.A 82 021606
[29]Gao X L,Chen A H,Tokatly I V,Kurth S 2012 Phys.Rev.B 86 235139
[30]Gao X L 2012 J.Phys.B 45 225304
[31]Gao X L,Asgari R 2008 Phys.Rev.A 77 033604
[32]Hu J H,Wang J J,Gao X L,Okumura M,Igarashi R,Yamada S,Machida M 2010 Phys.Rev.B 82 014202
[33]Campo V L 2015 Phys.Rev.A 92 013614
[34]Gao X L,Polini M,Rainis D,Tosi M P,Vignale G 2008 Phys.Rev.Lett.101 206402
[35]Li W,Gao X L,Kollath C,Polini M 2008 Phys.Rev.B 78 195109
[36]Takahashi M,Shiroishi M 2002 Phys.Rev.B 65 165104
[37]Ying Z J,Brosco V,Lorenzana J 2014 Phys.Rev.B 89 205130
[38]Wang C J,Chen A H,Gao X L 2012 Acta Phys.Sin.61 127501(in Chinese)[王婵娟,陈阿海,高先龙 2012物理学报61 127501]
PACS:67.25.bd,71.10.–wDOI:10.7498/aps.66.126701
Chemical potential-functional-theory about the properties of one-dimensional Hubbard model at fi nite temperature∗
Lu Zhan-Peng Wei Xing-Bo Liu Tian-Shuai Chen A-Hai Gao Xian-Long†
(Department of Physics,Zhejiang Normal University,Jinhua 321004,China)
7 January 2017;revised manuscript
26 March 2017)
In this paper,we numerically solve the thermodynamic Bethe-ansatz coupled equations for a one-dimensional Hubbard model at fi nite temperature and obtain the second order thermodynamics properties,such as the speci fi c heat,compressibility,and susceptibility.We fi nd that these three quantities could embody the phase transitions of the system,from the vacuum state to the metallic state,from the metallic state to the Mott-insulating phase,from the Mott-insulating phase to the metallic state,and from the metallic state to the band-insulating phase.With the increase of temperature,the thermal fl uctuation overwhelms the quantum fl uctuations and the phase transition points disappear due to the destruction of the Mott-insulating phase.But in the case of the strong interaction strength,the Mott-insulating phase is robust,embodying the compressibility.Furthermore,we study the thermodynamic properties of the inhomogeneous Hubbard model with trapping potential.Making use of the Bethe-ansatz results from the homogeneous Hubbard model,we construct the chemical potential-functional theory(µ-BALDA)for the inhomogeneous Hubbard model instead of the commonly used density-functional theory,in order to solve the in-convergence problem of the Kohn-Sham equation in the case of the divergence appearing in the exchange-correlation potential.We further point out a multi-dimensional bisection method which changes the Kohn-Shan equation into a problem of fi nding the fi xed points.Throughµ-BALDA we numerically solve the one-dimensional homogeneous Hubbard model of trapping potential.The density pro fi le and the local compressibility are obtained.We fi nd that at a given interaction strength,the metallic phase and the Mottinsulating phase are destroyed and the density pro fi le becomes a Guassian distribution with increasing temperature.To the metallic phase,Friedel oscillation caused by quantum fl uctuations is still visible at low temperature.With increasing temperature,Friedel oscillation will disappear.This situation re fl ects the fact that the thermal fl uctuation overwhelms the quantum fl uctuations.For the Mott-insulating phase,the Mott-insulating plateau is robust at a certain temperature and only the boundary of the Mott-insulating plateau is destroyed.With increasing temperature,the Mott insulating plateau will be destroyed.And the change of the local compressibility provides the information about such a change.So we conclude that the thermal fl uctuation destroys the original quantum phase.Through our analysis,we fi nd that theµ-BALDA can be used to study the fi nite temperature properties for the system of the exchange-correlation potential divergence with high efficiency.
thermodynamic Bethe-ansatz equations,compressibility,Hubbard model,chemical potentialfunctional theory
10.7498/aps.66.126701
∗国家自然科学基金(批准号:11374266)、新世纪优秀人才支持计划和浙江省自然科学基金(批准号:Z15A050001)资助的课题.
†通信作者.E-mail:gaoxl@zjnu.edu.cn
©2017中国物理学会Chinese Physical Society
http://wulixb.iphy.ac.cn
*Project supported by the National Natural Science Foundation of China(Grant No.11374266),the Program for New Century Excellent Talents in University,China,and the Natural Science Foundation of Zhejiang Province,China(Grant No.Z15A050001).
†Corresponding author.E-mail:gaoxl@zjnu.edu.cn
