线宽增强因子对光反馈半导体激光器混沌信号生成随机数性能的影响∗

韩韬1)2) 刘香莲1)2)† 李璞1)2) 郭晓敏1)2) 郭龑强1)2) 王云才1)2)

1)(太原理工大学,新型传感器与智能控制教育部重点实验室,太原 030024)

2)(太原理工大学物理与光电工程学院,光电工程研究所,太原 030024)

线宽增强因子对光反馈半导体激光器混沌信号生成随机数性能的影响∗

韩韬1)2) 刘香莲1)2)† 李璞1)2) 郭晓敏1)2) 郭龑强1)2) 王云才1)2)

1)(太原理工大学,新型传感器与智能控制教育部重点实验室,太原 030024)

2)(太原理工大学物理与光电工程学院,光电工程研究所,太原 030024)

(2017年1月6日收到;2017年3月21日收到修改稿)

基于光反馈半导体激光器产生的宽带混沌信号作为物理熵源生成物理随机数已得到广泛研究.线宽增强因子的存在会导致半导体激光器出现大量不稳定动态特性,因此,本文着重研究半导体激光器的线宽增强因子对生成随机数性能的影响.数值仿真结果表明:随着线宽增强因子的增加,光反馈半导体激光器输出混沌信号的延时峰值逐渐减小、最大李雅普诺夫指数逐渐增大.基于不同线宽增强因子下产生的混沌信号提取随机数,并利用NIST SP 800-22软件对生成随机数的性能进行测试.测试结果表明,选取线宽增强因子较大的半导体激光器产生混沌信号作为物理熵源易于生成性能良好的随机数.

光反馈半导体激光器,线宽增强因子,混沌,随机数

1 引 言

在信息安全、测试及工程实践等领域,随机数扮演着重要的角色[1].在信息安全领域,随机数可应用于密钥管理、数字签名、身份认证、安全协议、网上银行、在线购物和信息加密等方面的众多安全技术中,以确保信息的机密性;在测试领域,随机数可通过眼图和误码率的测试来检测通讯系统的传输质量;在工程实践领域,雷达的测距信号、光时域反射仪的探测信号、遥控遥测中的测控信号、数字通信中的群同步、码分多址中的地址码和扩频码都应用了随机数.

随机数一般分为两种:伪随机数和真随机数.其中伪随机数是由初始种子经过一个确定算法生成的.伪随机数发生器具有易构建、速率高的特点,但其获取的随机数有限且存在周期性,如果被应用于信息系统会造成极大的安全事故.真随机数则是由物理熵源产生的,与伪随机数相比,真随机数具有不可预测性,因而具有更高的安全性.真随机数采用过的物理熵源的种类繁多,像早期的鼠标抖动,以及后来采用的电子噪声[2,3]、频率抖动[4]、辐射衰变[5]、单光子发射/探测[6−8]等.此外,利用量子力学基本量的完全随机性以及采集生物的无规律行为也可以用作真随机数发生器的熵源[9−11].但是由于熵源带宽的限制,这些真随机数发生器产生随机数的速率多处于Mbit/s量级,无法满足当前高速大容量通信的需要.

在光反馈、光注入或光电反馈等外部扰动下,半导体激光器可以产生宽带混沌激光信号.与光注入、光电反馈相比,光反馈半导体激光器的光源结构简单且易于集成.最近,基于光反馈半导体激光器的宽带混沌信号[12,13]作为物理熵源生成的高速物理随机数引起了世界各国研究者的关注.例如,2008年开始,基于混沌激光产生的物理随机数的速率能够达到Gbit/s的量级[14],随后以色列巴依兰大学Reider等[15,16]、中国香港城市大学的Li和Chan[17,18]、希腊雅典大学Argyris等[19]、国内西南大学[20,21]、西南交通大学[22]以及太原理工大学的课题组[23]都对基于光反馈混沌激光产生高速的物理随机数进行了大量研究.在已报道的混沌激光随机数方案中,可采用延迟异或[23]、多级差分[16]等后处理方法来提高随机数的速率和随机性,另外也可以通过优化混沌熵源来改善随机数的性能.

近些年来,反馈强度、外腔长度、激光器的偏置电流等混沌熵源外部参量对基于光反馈半导体激光器的混沌信号产生的随机数性能方面的影响已有报道[24−28].此外,激光器的内部参量对半导体激光器动态特性的影响也引起了各国研究者的广泛关注.例如,Hwang和Liu[29]分别探究了载流子寿命、光子寿命和微分增益系数对半导体激光器动态特性的影响;Hwang和Liang[30]以及张明江等[31]也分别分析了线宽增强因子对激光器单周期振荡的影响;Wieczorek课题组研究了线宽增强因子与倍周期分叉动态特性的关系[32],并讨论比较了不同类型激光器的线宽增强因子对本身动力学特性的影响[33];Pochet等[34]研究了线宽增强因子对量子点激光器的二倍周期及混沌特性的影响.但是,激光器的内部参量对随机数性能有何影响尚未进行深入研究.在激光器内部参量中,由于线宽增强因子对半导体激光器的动态特性有很大的影响[33,35],因此深入研究线宽增强因子对基于半导体激光器系统产生随机数性能的影响具有重要的意义.

2 系统结构

利用外腔光反馈半导体激光器产生宽带混沌信号作为物理熵源生成高速的物理随机数的系统方案如图1所示.分布式反馈半导体激光器(DFB)输出的光通过偏振控制器(PC)控制光的偏振态,经过光纤耦合器(OC)分成两路.其中一路光经由可调光衰减器(VOA)控制光的强度,并经光纤反射镜(FM)反馈回DFB;另一路光通过光隔离器(OI)输出作为提取随机数的物理熵源.OI确保混沌激光单向传输,以免DFB损伤.通过OI的混沌激光信号经过光电探测器(PD),将光信号转换为电信号,并去除直流分量,然后经过8位模数转换器(ADC)转换输出8位二进制信号.从8位二进制信号中提取后m最低有效位(LSBs),并利用缓冲器对该m位二进制信号进行延迟异或(XOR),得到最终的二进制码.利用NIST SP 800-22测试软件对最终得到的二进制码进行随机性认证,如果所有的测试项都能通过,那么所得到的二进制码为物理真随机数.

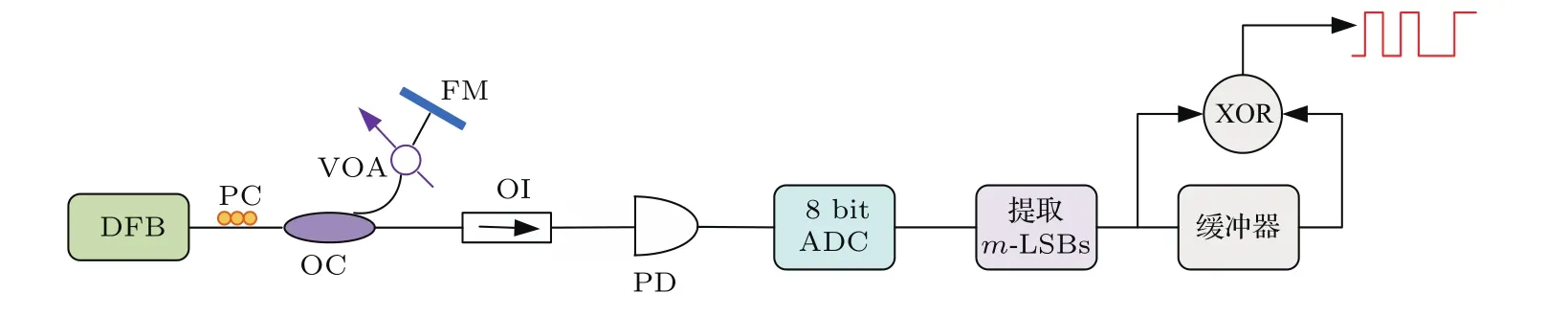
图1 (网刊彩色)基于光反馈混沌激光产生高速的物理随机数示意图(DFB为分布式反馈激光器,PC为偏振控制器,OC为光纤耦合器,VOA为可调光衰减器,FM为光纤反射镜,OI为光隔离器,PD为光电转换器,ADC为模数转换器,LSBs为最低有效位,XOR为异或)Fig.1.(color online)Schematic diagram of the generation of high-speed physical random number based on optical feedback semiconductor laser(DFB,distributed feedback laser;PC,polarization controller;OC,optical coupling;VOA,variable optical attenuator;FM, fi ber mirror;OI,optical isolator;PD,photo detector;ADC,analog-to-digital converter;LSBs,least signi fi cant bits;XOR,exclusive-OR).

3 理论模型

描述DFB在光反馈作用下的动力学特性的速率方程为

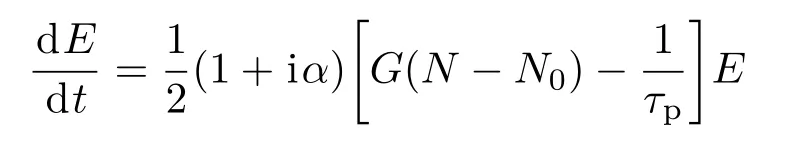
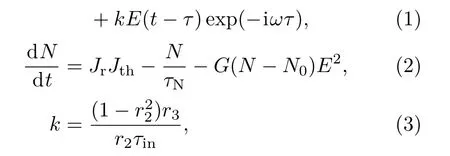
式中,E为慢变场振幅,N为载流子数密度,α为线宽增强因子,G为微分增益系数,N0为透明载流子密度,τp为光子寿命,τin为光在激光腔内往返的时间,τ为光在外腔中的往返时间,Jr为注入电流比,τN为载流子寿命,ω为DFB的中心角频率Jth为阈值电流密度k为反馈强度,r2为内腔反射率,r3为外腔反射率.

混沌激光的时延特性及复杂度是衡量混沌激光质量的两个重要的参数,通常采用自相关函数、互信息等方法分析混沌激光系统的延时特征,采用最大李雅普诺夫指数(最大李指数),Kolmogorov-Sinai熵、相关维数、排列熵等方法分析混沌激光系统的复杂度.本文采用的是自相关函数法和最大李指数法分别分析时延特性和复杂度.其中自相关函数的定义为

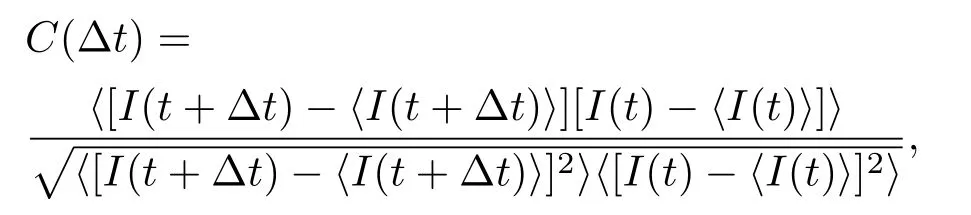
式中,I为激光器输出的信号的强度,∆t为移动时间,〈·〉表征时间平均.

最大李指数是诊断和描述动态系统混沌的重要参数[36].对于非线性系统,只要其最大李指数为正数,系统就会呈现混沌特性.而一般情况下,李指数取值越大,两个临近轨道按照指数分离的速率越快,因此,由相邻两轨道中的其中一条轨道来预测另一条轨道的难度越大,相应的时间序列也就越难以预测,因而可以将最大李指数的大小作为衡量混沌序列复杂度的一个标准.

4 结果与讨论

利用四阶龙格库塔法对方程(1),(2)和(3)进行数学求解.数值模拟中用到的参量取值如表1所列.

由于不同材料、结构类型的半导体激光器的线宽增强因子各有不同,例如掩埋异质结结构典型值为6左右.图2(a)和图2(b)分别给出了线宽增强因子为6时的光反馈半导体激光器输出的混沌信号的时间序列和相应的功率谱.光反馈半导体激光器一般会经历定态、单周期、准周期后进入到混沌状态.从图2可以看到,光反馈半导体激光器输出的时间序列呈现出无规则的状态,频谱呈现连续分布,这表明光反馈半导体激光器输出的信号为混沌信号.

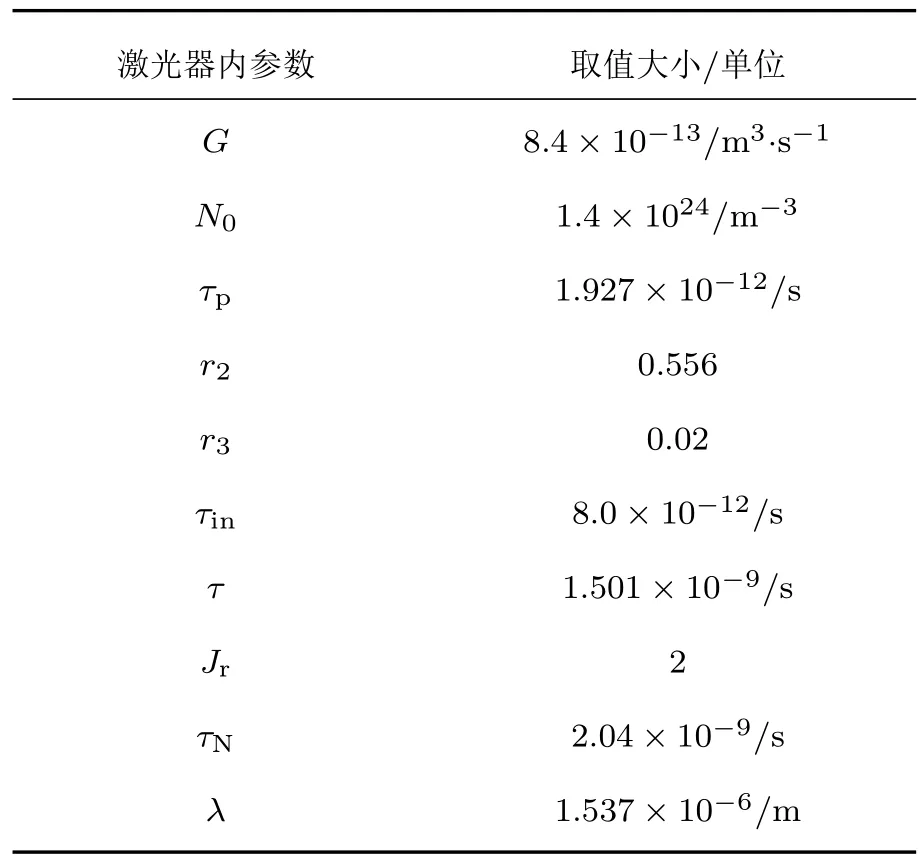
表1 基于光反馈混沌激光系统的不同参量取值Table 1.Di ff erent parameters of chaotic system based on the optical feedback semiconductor laser.

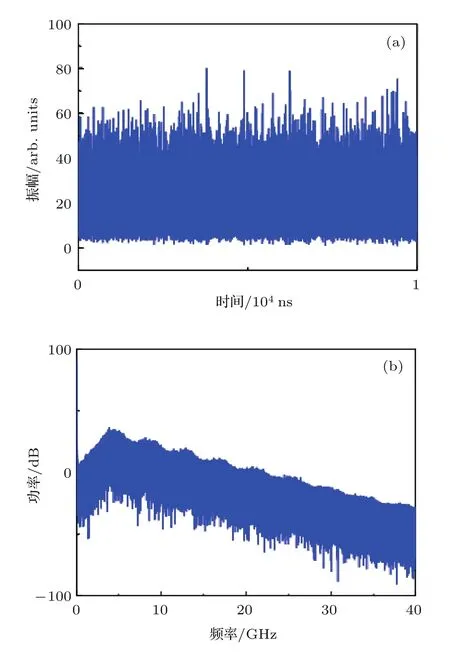
图2 (a)混沌信号的时间序列;(b)对应混沌信号的功率谱Fig.2.(a)Time series and(b)associated power spectrum under α=6.

图3(a)—(c)分别是线宽增强因子为2,4,7的情况下光反馈半导体激光器输出混沌信号的自相关函数谱.混沌信号的延时峰值是在外腔延时时间τ附近的[1 ns,2 ns]内自相关函数的最大值.图3中插图表示的是移动时间[0 ns,10 ns]的自相关函数谱,从图中可以看到,随着线宽增强因子的增大延时峰值逐渐减小.

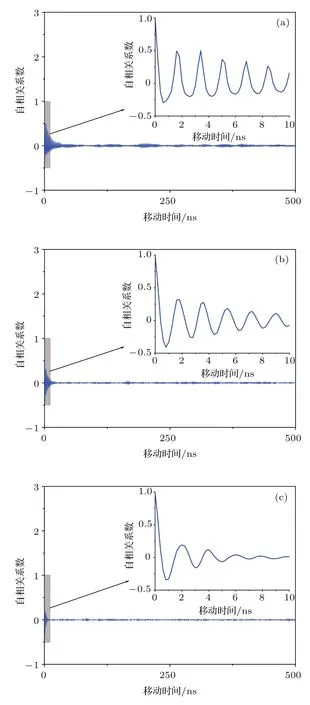
图3 不同线宽增强因子下外腔半导体激光器输出自相关函数谱 (a)α=2;(b)α=4;(c)α=7Fig.3. Autocorrelation functions under di ff erent linewidth enhancement factors:(a)α=2;(b)α=4;(c)α=7.

对于时延的动态系统,求取最大李指数要考虑外腔延时时间τ.接下来,为了研究线宽增强因子对混沌信号特性的影响规律,数值模拟不同的线宽增强因子下混沌信号的延时峰值和最大李指数的变化情况,结果如图4(a)和图4(b)所示.从图4可以明显地看出随线宽增强因子的增加,延时峰值逐渐减小、最大李指数逐渐增加.因此,为了产生高质量的混沌熵源,尽量选取线宽增强因子较大的半导体激光器.

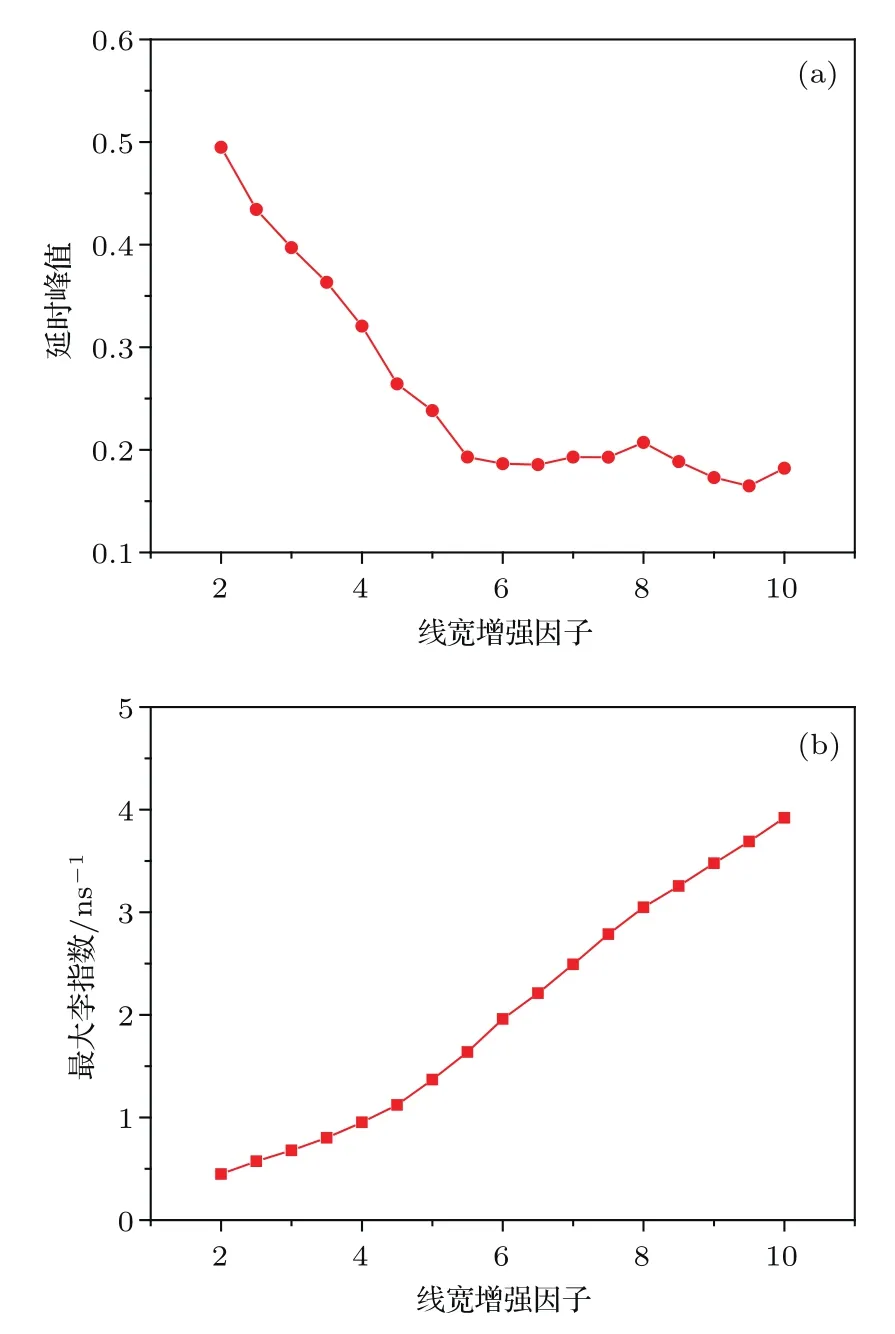
图4 (a)混沌信号的延时峰值随线宽增强因子的变化;(b)混沌信号的最大李指数随线宽增强因子的变化Fig.4. (a)Time delay characteristic peak of the chaotic signal with linewidth enhancement factor;(b)the maximum Lyapunov exponent of the chaotic signal with linewidth enhancement factor.

进一步分析利用外腔半导体激光器产生的混沌信号经过后续处理后产生的二进制序列的特性.混沌信号经过8位ADC的采样量化转换成为二进制信号,该信号再与通过缓冲器延时20.6 ns的二进制信号做XOR处理,得到最终的二进制码,其中ADC的采样率为5 GHz.为了观察二进制码的特性,图5给出了线宽增强因子为6时混沌信号保留后m位LSBs的二进制码转换为十进制的统计分布直方图,图5(a)—(e)分别对应于m从8减小到4,图5(f)为保留后4位LSBs后再做XOR处理的输出结果.在此图中横坐标表示量化后的幅值,即将信号幅值分为2m个单元,纵坐标则表示每个单元幅值的分布概率.从图5可以看到,当保留全部8位有效位时,信号幅值的分布很不均匀,不可以直接作为随机数.但随着保留的位数逐渐减小,幅值分布的均匀性逐渐得到明显改善.

最后,运用美国国家标准技术研究所提供的NIST SP 800-22测试软件对线宽增强因子为6且保留4-LSBs延迟XOR生成的二进制码进行测试.NIST包含15个测试项,每个测试项都是针对被测序列的某一特性进行检测.测试结束后,会得到两个结果:P-VALUE值和PROPORTION值.测试采用1000组1M的数据点,显著水平β设置为0.01,只有最终测试结果的P-VALUE大于0.0001且PROPORTION大于0.9806才算通过(对于包含多个子项的测试项,选择其中最小的值来评判).图6(a)和图6(b)分别为NIST各测试项对应的P-VALUE值和PROPORTION值,横坐标数字1—15分别表示NIST测试的15个测试项,分别为频数、块内频数、累加和、游程、块内最长游程、矩阵秩、离散傅里叶变换、非重叠模块匹配、重叠模块匹配、通用统计、近似熵、随机偏移、随机偏移变量、串行和线性复杂度.测试结果表明,所产生的二进制码全部通过了NIST的测试标准.

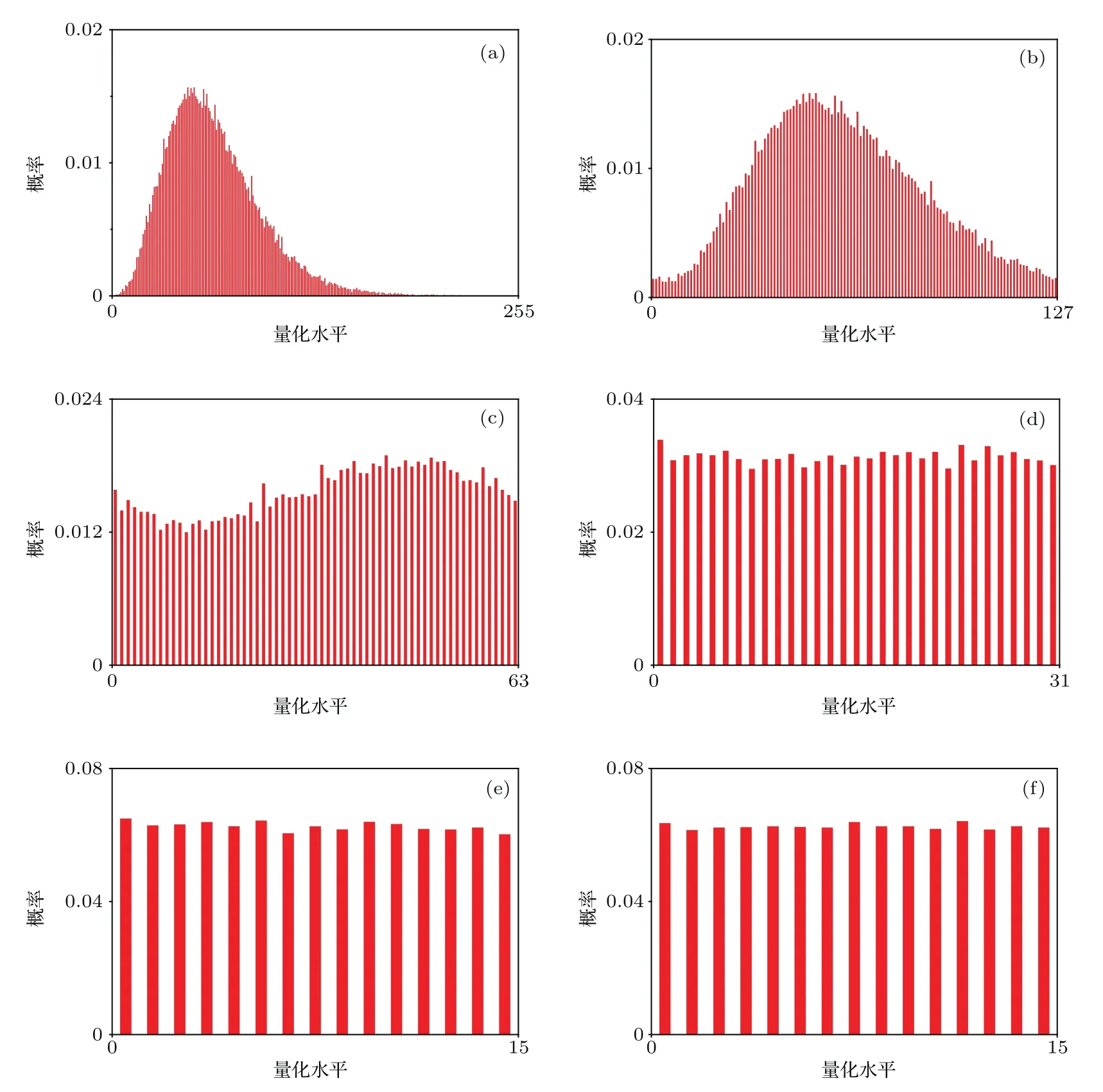
图5 激光器输出的混沌信号保留后m位有效位后的统计分布直方图 (a)—(e)分别对应m从8减小到4;(f)保留后4位有效位做异或处理的输出结果Fig.5.Statistical histogram of the retained m-LSBs binary data stream obtained by chaotic signal under α=6:(a)–(e)m decreases from 8 to 4;(f)4-LSBs are retained for bitwise XOR operation.

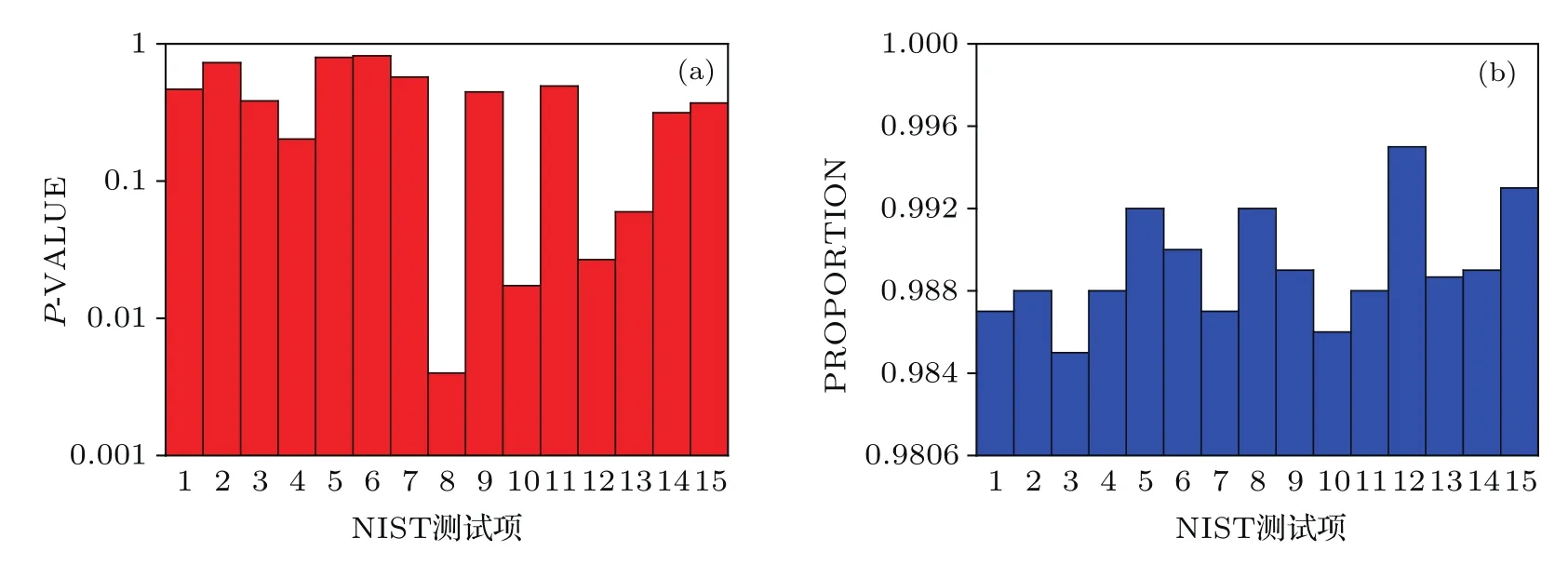
图6 (网刊彩色)(a)NIST各测试项的P-VALUE值;(b)NIST各测试项的PROPORTION值;横坐标数字1—15分别表示NIST测试的15个测试项,分别为频数、块内频数、累加和、块内最长游程、游程、矩阵秩、离散傅里叶变换、非重叠模块匹配、重叠模块匹配、通用统计、近似熵、随机偏移、随机偏移变量、串行和线性复杂度Fig.6.(color online)(a)P-VALUE of each test item;(b)PROPORTION of each test item;the numbers on the horizontal axis represent 15 di ff erent statistical tests in the NIST test suit,which are named as “Frequency”, “Block frequency”, “Cumulative sums”, “Longest-run”, “Runs”, “Rank”, “FFT”, “Non-Overlapping templates”, “Overlapping templates”, “Universal”, “Approximate entropy”, “Random excursion”,“Random excursions variant”,“Serial” and “Linear complexity”,respectively.

在不同的线宽增强因子下,图7中黑线与红线分别为研究了保留后4位和保留后5位LSBs延迟XOR所生成的二进制码通过NIST SP 800-22软件测试后的项数.如果选择保留后4位LSBs形成最后的XOR二进制码,当线宽增强因子大于4时能通过15项测试,即此时所输出的为物理真随机数;如果选择保留后5位LSBs形成最后的XOR二进制码,当线宽增强因子大于5时能通过15项测试,此时ADC采样率取5 GHz,故所能达到的最高速率为25 Gbit/s.

由于混沌信号的带宽是影响生成随机数速率的重要因素,需研究混沌信号的带宽随线宽增强因子的变化情况.数值分析结果显示:在其他参量一定的情况下,随着线宽增强因子的增加,带宽(带宽定义为:从0频算起,包含功率谱总能量80%的频率范围)略微增大,但变化不明显,基本保持5 GHz左右.在本文中,所获随机数速率由保留的有效位数与采样率的乘积决定,其中采样率受限于混沌信号的带宽.因此为了能够获得较高速率的随机数,文中设置采样率为5 GHz,与混沌信号的带宽基本一致.

在半导体激光器的诸多内部参量中,线宽增强因子α是一个极其重要的参量,表征半导体激光器由于载流子密度起伏导致的线宽展宽和啁啾特性[29,30],正是由于线宽增强因子的存在导致半导体激光器出现大量不稳定动态特性.不同材料、不同结构类型的半导体激光器的线宽增强因子有所不同,当α增加时,激光振荡模式及边带模式增加,光谱成分丰富,混沌的复杂度提高.由于光谱成分增多,激光腔谐振周期变多,色散效应增强,削弱了激光器的外腔长信息,减小了混沌的周期性.所以,随着α增大,半导体激光器产生混沌激光的延时峰值逐渐减小、最大李指数逐渐增大.基于混沌熵源产生随机数的性能一定程度上取决于熵源好坏,因此可以通过优化熵源的性能提高随机数的质量.本文分析讨论得到:随着线宽增强因子α增加,混沌熵源性能逐步得到改善.所以,选取较大的线宽增强因子,容易获得性能良好的随机数.

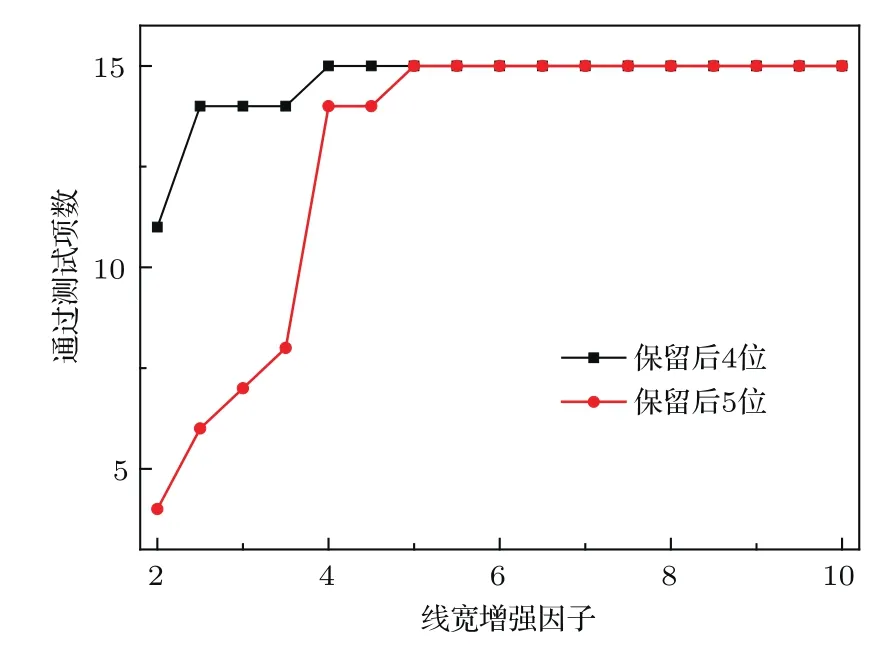
图7 (网刊彩色)ADC采样率为5 GHz时,保留后m位XOR的二进制码通过NIST SP 800-22软件测试的项数随线宽增强因子的变化 (a)保留后4位;(b)保留后5位Fig.7.(color online)Dependences of the number of passed terms of NIST SP 800-22 test for m-bit XOR binary data on the linewidth enhancement factor under ADC with sampling rate of 5 GHz:(a)4-LSBs;(b)5-LSBs.

5 结 论

本文对基于光反馈半导体激光器输出的混沌激光信号作为物理熵源,经过光电转换、ADC采样量化以及保留后m位和XOR处理后所生成的m位XOR二进制码的随机性与线宽增强因子的依赖关系进行了理论研究.研究结果表明:光反馈半导体激光器所产生的混沌信号的延时峰值随线宽增强因子的增加呈现逐渐减小的过程,而混沌信号的最大李指数随线宽增强因子的增加逐渐增大;由不同线宽增强因子下光反馈半导体激光器输出的混沌信号作为混沌熵源,经过后续处理后所获得的二进制码通过NIST SP 800-22软件测试的项目数与线宽增强因子的大小紧密相关.对于采样率为5 GHz的ADC,保留后4位LSBs的二进制码,当线宽增强因子大于4时能通过15项测试;保留后5位LSBs的二进制码,当线宽增强因子大于5时能通过15项测试,此时能获取的二进制码的最高速率为25 Gbit/s.同时,降低所保留的位数m将使能得到物理真随机数输出的线宽增强因子范围略增大,但相应的随机数的速率减小.

[1]Li P 2014 Ph.D.Dissertation(Taiyuan:Taiyuan University of Technology)(in Chinese)[李璞 2014博士学位论文(太原:太原理工大学)]

[2]Xu P,Wong Y L,Hoduchi T K,Abshire P A 2006 Electron.Lett.42 1346

[3]Petrie C S,Connelly J A 2000 IEEE Trans.Circuits I 47 615

[4]Bucci M,Germani L,Luzzi R,Tri fi letti A,Varanonuovo M 2003 IEEE Trans.Comput.52 403

[5]Schmidt H 1970 J.Appl.Phys.41 462

[6]Stipčević M,Rogina B M 2007 Rev.Sci.Instrum.78 045104

[7]Martino A J,Morris G M 1991 Appl.Opt.30 981

[8]Jennewein T,Achleitner U,Weihs G,Weinfurter H,Zeilinger A 2000 Rev.Sci.Instrum.71 1675

[9]Guo H,Liu Y,Dang A H,Wei W 2009 Chin.Sci.Bull.54 3651(in Chinese)[郭弘,刘钰,党安红,韦韦 2009科学通报54 3651]

[10]Ren M,Wu E,Liang Y,Jian Y,Wu G,Zeng H 2011 Phys.Rev.A 83 023820

[11]Zhou Q,Hu Y,Liao X F 2008 Acta Phys.Sin.57 5413(in Chinese)[周庆,胡月,廖晓峰2008物理学报57 5413]

[12]Zhang M J,Liu T G,Wang A B,Zheng J Y,Meng L N,Zhang Z X,Wang Y C 2011 Opt.Lett.36 1008

[13]Zhao Q C,Yin H X 2013 Laser Optoelectron.Prog.50 030003(in Chinese)[赵清春,殷洪玺 2013激光与光电子学进展50 030003]

[14]Uchida A,Amano K,Inoue M,Hirano K,Naito S,Someya H,Oowada I,Kurashige T,Shiki M,Yoshimiri S,Yoshimura K,Davis P 2008 Nat.Photon.2 728

[15]Reidler I,Aviad Y,Rosenbluh M,Kanter I 2009 Phys.Rev.Lett.103 024102

[16]Kanter I,Aviad Y,Reidler I,Cohen E,Rosenbluh M 2010 Nat.Photon.4 58

[17]Li X,Chan S 2012 Opt.Lett.37 2163

[18]Li X,Chan S 2013 IEEE J.Quantum Electron.49 829

[19]Argyris A,Deligiannidis S,Pikasis E,Bogris A,Syvridis D 2010 Opt.Express 18 18763

[20]Tang X,Wu J G,Xia G Q,Wu Z M 2011 Acta Phys.Sin.60 110509(in Chinese)[唐曦,吴加贵,夏光琼,吴正茂2011物理学报60 110509]

[21]Wu J G,Tang X,Wu Z M,Xia G Q,Feng G Y 2012 Laser Phys.22 1476

[22]Li N Q,Kim B,Chizhevsky V N,Locquet A,Bloch M,Citrin D S,Pan W 2014 Opt.Express 22 6634

[23]Wang A,Li P,Zhang J,Zhang J,Zhang J,Li L,Wang Y 2013 Opt.Express 21 20452

[24]Yang H B,Wu Z M,Tang X,Wu J G,Xia G Q 2015 Acta Phys.Sin.64 084204(in Chinese)[杨海波,吴正茂,唐曦,吴加贵,夏光琼2015物理学报64 084204]

[25]Hirano K,Amano K,Uchida A,Naito S,Inoue M,Yoshimiri S,Yoshinura K,Davis P 2009 IEEE J.Quantum Electron.45 1367

[26]Zhang J B,Zhang J Z,Yang Y B,Liang J S,Wang Y C 2010 Acta Phys.Sin.59 7679(in Chinese)[张继兵, 张建忠,杨毅彪,梁君生,王云才2010物理学报59 7679]

[27]Xiao B J,Hou J Y,Zhang J Z,Xue L G,Wang Y C 2012 Acta Phys.Sin.61 150502(in Chinese)[萧宝瑾,侯佳音,张建忠,薛路刚,王云才2012物理学报61 150502]

[28]Zhang J Z,Wang Y C,Xue L G,Hou J Y,Zhang B B,Wang A B,Zhang M J 2012 Appl.Opt.51 1709

[29]Hwang S K,Liu J M 2000 Opt.Commun.183 195

[30]Hwang S K,Liang D H 2006 Appl.Phys.Lett.89 061120

[31]Zhang M J,Liu T G,Li J X,Wang Y C 2011 Acta Phot.Sin.40 542(in Chinese)[张明江,刘铁根,李静霞,王云才2011光子学报40 542]

[32]Wieczorek S,Chow W W 2005 Opt.Commun.246 471

[33]Wieczorek S,Krauskopf B,Simpson T B,Lenstra D 2005 Phys.Report 416 1

[34]Pochet M,Naderi N A,Terry N,Kovanis V,Lester L F 2009 Opt.Express 17 20623

[35]Liu G,Jin X,Chuang S L 2001 IEEE Photon.Technol.Lett.13 430

[36]Yang S Q,Zhang X H,Zhao C A 2000 Acta Phys.Sin.49 636(in Chinese)[杨绍清,章新华,赵长安2000物理学报49 636]

PACS:42.55.Px,05.45.Gg,05.40.–aDOI:10.7498/aps.66.124203

In fl uence of the linewidth enhancement factor on the characteristics of the random number extracted from the optical feedback semiconductor laser∗

Han Tao1)2)Liu Xiang-Lian1)2)†Li Pu1)2)Guo Xiao-Min1)2)Guo Yan-Qiang1)2)Wang Yun-Cai1)2)

1)(Key Laboratory of Advanced Transducers and Intelligent Control System of Ministry of Education,Taiyuan University of Technology,Taiyuan 030024,China)
2)(Institute of Optoelectronic Engineering,College of Physics and Optoelectronics,Taiyuan University of Technology,Taiyuan 030024,China)

6 January 2017;revised manuscript

21 March 2017)

Random numbers play an important role in many fi elds,including information security,testing and engineering practice.Especially in information security,generation of secure and reliable random numbers,they have a signi fi cant in fl uence on national security, fi nancial stability,trade secrets and personal privacy.

Generally,random number generators can be classi fi ed as two main types:pseudo random number generators and physical random number generators.Pseudo random numbers with high speed are generated by software algorithms,but the inherent periodicity will cause serious hidden dangers when they are used in information security.Random numbers based on physical entropy sources(such as electronic thermal noise,frequency jitter of oscillator,quantum randomness)can produce reliable random numbers.However,due to the limitation of traditional physical source bandwidth,their generation speeds are at a level of Mbit/s typically,which cannot meet the needs of the current high-speed and largecapacity communication.

In 2008,Uchida et al.(2008 Nat.Photon.2 728)realized the physical random number of 1.7 Gbit/s by using a wideband chaotic laser for the fi rst time.The emergence of wideband physical entropy sources such as chaotic laser greatly promote the rapid development of the physical random number generators.As far as we know,a semiconductor laser can generate wideband chaotic signals under external disturbances such as optical feedback,optical injection or photoelectric feedback.However,compared with the structures of other two lasers,the structure of the optical feedback semiconductor laser is simple and easy to integrate.Therefore,chaotic signals have received great attention to produce high-speed physical random number extracted from the optical feedback semiconductor laser.In the reported schemes,a variety of post-processing methods are used to improve the speed and randomness of random numbers.Besides,optimizing the chaotic entropy source can also improve the performance of random number.

So far,the in fl uence of internal parameters on the dynamic characteristics of semiconductor lasers has attracted wide attention.The linewidth enhancement factor is one of the key parameters for a semiconductor laser.The values of linewidth enhancement factor are di ff erent,depending on the type of semiconductor laser.The existence of linewidth enhancement factor results in a large number of unstable dynamic characteristics of semiconductor lasers.Therefore,it is of great signi fi cance for studying the in fl uence of the linewidth enhancement factor on performance of random numbers.

In this paper,we focus on the in fl uence of the linewidth enhancement factor on the randomness of the obtained random numbers.The time delay characteristics and complexity are two important parameters to measure the quality of chaotic signals.The simulation results show that with the increase of the linewidth enhancement factor,the time delay characteristic peak of the chaotic signal from an optical feedback semiconductor laser decreases gradually,meanwhile,the maximum Lyapunov exponent of chaotic signal increases gradually.The randomness of random numbers,generated by the chaotic signal from the optical feedback semiconductor laser under di ff erent linewidth enhancement factors,is tested by NIST SP 800-22.The test results show that semiconductor laser with larger linewidth enhancement factor is chosen as a physical entropy source to generate random numbers with high quality.

optical feedback semiconductor laser,linewidth enhancement factor,chaos,random number

10.7498/aps.66.124203

∗山西省自然科学基金(批准号:201601D021021)、国家自然科学基金(批准号:61671316,61505137,61405138,61505136)、国家自然科学基金科学仪器基础研究专款(批准号:61227016)、国家国际科技合作专项(批准号:2014DFA50870)和太原理工大学引进人才基金(批准号:tyutrc201387a)资助的课题.

†通信作者.E-mail:liuxianglian@tyut.edu.cn

©2017中国物理学会Chinese Physical Society

http://wulixb.iphy.ac.cn

*Project supported by the Natural Science Foundation of Shanxi Province,China(Grant No.201601D021021),the National Natural Science Foundation of China(Grant Nos.61671316,61505137,61405138,61505136),the Special Fund For Basic Research on Scienti fi c Instruments of the National Natural Science Foundation of China(Grant No.61227016),the Funds for International Cooperation and Exchange of the National Natural Science Foundation of China(Grant No.2014DFA50870),and the Quali fi ed Personnel Foundation of Taiyuan University of Technology(Grant No.tyutrc201387a).

†Corresponding author.E-mail:liuxianglian@tyut.edu.cn