带可乘白噪声的Schrödinger格点系统的随机吸引子*

崔红珍, 周盛凡

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)



带可乘白噪声的Schrödinger格点系统的随机吸引子*

崔红珍, 周盛凡

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

主要考虑带可乘白噪声的随机Schrödinger格点系统的随机吸引子的存在性.首先,利用Ornstein-Uhlenbeck过程将具白噪声的随机Schrödinger格点系统转化成以随机变量为系数而无噪声的随机格点系统;其次,研究该随机系统的初值问题的整体解的存在唯一性,其解映射可以生成随机动力系统;最后,证明该随机动力系统的有界随机吸收集和随机吸引子的存在性.

随机吸引子;可乘白噪声;Schrödinger格点系统；存在性

0 引 言

格点动力系统(LDS)在生物学、化学、模式识别、图像处理、电子工程及材料科学等领域中应用广泛.近年来,具有不确定噪声扰动的随机格点动力系统(SLDS)也是研究的热门课题.文献[1-7]研究了一些自治和非自治的LDS、SLDS的吸引子的存在性.

本文主要考虑如下两类无穷格点上带可乘白噪声的Schrödinger系统:

(1)

(2)

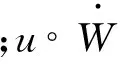
对于没有噪声扰动的Schrödinger格点系统(即式(1)中a=0),Karachalios等[7]研究了它的整体吸引子的存在性;Chen等[8]证明了带时滞项时它的整体吸引子的存在性;周盛凡等[9-10]证明了它的指数吸引子的存在性.当a≠0,即系统(1)和系统(2)存在可乘白噪声扰动时，其吸引子未见有任何研究.本文将结合文献[11]给出的随机吸引子存在的判据来证明系统(1)和(2)存在随机吸引子.

1 系统(1)的随机吸引子

1.1 方程转化

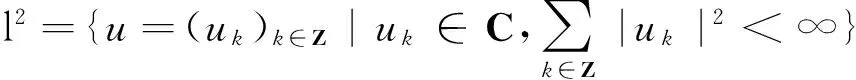
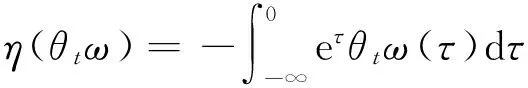
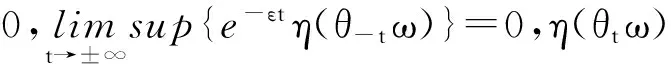
系统(1)可以写成如下等价的向量形式:

(3)

式(3)中:u=(uk)k∈Z;g=(gk)k∈Z;h(|u|2)u=(h(|uk|2)uk)k∈Z.

对系统(1)中的g与h(s)作如下假设:

(A1)g=(gk)k∈Z∈l2;

(A2)h(s)∈C(R,R),且关于s局部Lipschitz连续,即对R上的任一有界区间I,存在L=L(I)>0,使得∀s1,s2∈I,|h(s1)-h(s2)|≤L(I)|s1-s2|;

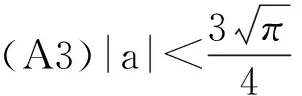
令x=ue-aη(θtω),则x与u在l2上同构,系统(3)等价于

(4)

1.2 全局解的存在唯一性

定理1 若假设(A1)～(A2)成立,则对∀ω∈Ω,x0∈l2,系统(4)存在唯一解x(·)=x(·,ω,x0)∈C([0,+∞),l2)∩C1((0,+∞),l2),x(·)关于x0连续,且解x(t,ω,·)生成一个由(Ω,F,P,(θt)t∈R)驱动取值于l2的连续随机动力系统{x(t,ω)}t≥0,ω∈Ω(随机动力系统的定义见文献[2]).

证明 1)令Q(θtω,x)=ih(|x|2e2aη(θtω))x-ige-aη(θtω)+aη(θtω)x,则∀ω∈Ω,t∈[0,p]⊂R+,Q(θtω,x)在l2的有界集B上关于x是Lipschitz连续的.

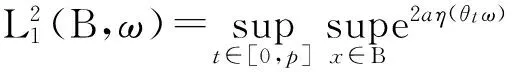
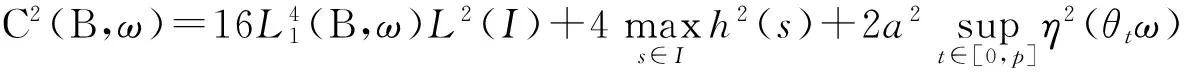
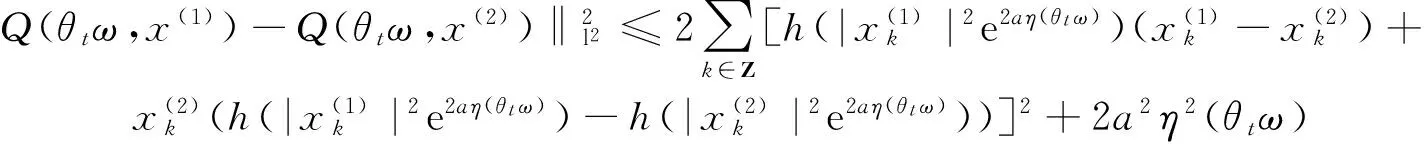
C2(B,ω)‖x(1)-x(2)‖2.

由于η(θtω)关于t连续,所以Q(θtω,x)关于t连续.又知g∈l2,由解的存在唯一性可得，系统(4)存在唯一局部解x(·,ω,x0)∈C([0,Tmax),l2)∩C1((0,Tmax),l2),其中x0=x(0,ω,x0)且[0,Tmax)是解的最大存在区间.

2)证明Tmax=+∞.令系统(4)与x作内积,取实部可得

(5)

经计算可得,

(6)

(7)

综合式(5)～式(7)可得

(8)

对式(8)从0到t应用Gronwall不等式可得

(9)

从而当t为有限数时，‖x(t)‖2有限,即Tmax=+∞.故x(t)是系统(4)的全局解.

3)结合1)和2)易得x(·,ω,x0)关于x0连续.定理1证毕.

1.3 随机吸引子的存在性

下面主要讨论{x(t,ω)}t≥0,ω∈Ω在l2上的随机吸收集和随机吸引子的存在性.

定理2 若假设(A1)～(A3)成立,则{x(t,ω)}t≥0,ω∈Ω存在一个缓增随机吸收集

其中,

则K(ω)满足:对于l2上任一缓增随机集Γ(ω),存在TΓ(ω)≥0,使得对∀t≥TΓ(ω),ω∈Ω,均有x(t,ω,Γ(θ-tω))⊆K(ω).

证明 令Γ(ω)是l2中的一个缓增集,x0∈Γ(ω),对式(9)应用拉回映射θ-t:ω|→θ-tω及积分变换,可得

‖x(t,θ-tω,x0(θ-tω))‖2≤

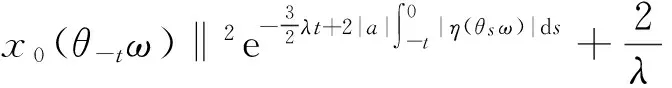
(10)

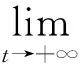
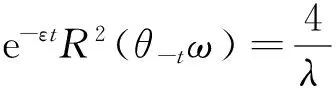
因此,R(ω)是一个缓增随机变量.记

则K(ω)是有界闭的缓增随机集.由式(10)得,它为{x(t,ω)}t≥0,ω∈Ω的一个随机吸收集.定理2证毕.

定理3 若假设(A1)～(A3)成立,则{x(t,ω)}t≥0,ω∈Ω存在随机吸引子γ(ω),且

其中,K(ω)是定理2中定义的随机吸收集.则γ(ω)满足：1)γ(ω)是随机紧集;2)γ(ω)是不变的,即∀t≥0,x(t,ω)γ(ω)=γ(θtω);3)γ(ω)吸引任意缓增随机集.

证明 首先证明∀ε>0,ω∈Ω,∃T′(ε,ω,K(ω))>0,M′(ε,ω)∈N,使得系统(4)满足初值x0∈K(θ-tω)∩l2的解x=(xk)k∈Z有如下性质:

选取递增的光滑函数f∈C(R+,R),使得

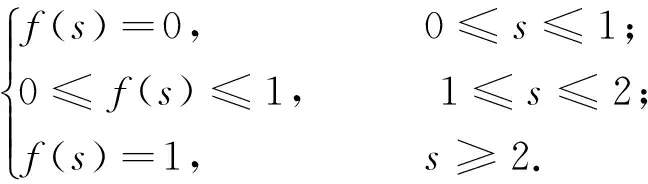
且对∀s∈R+,均有|f′(s)|≤f0(正常数).

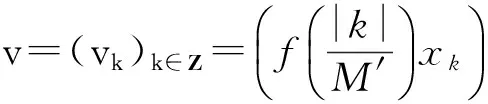
(11)

经计算可得:当t≥TK(ω)时,

(12)

(13)

(14)

(15)

综合式(11)～式(15)可得

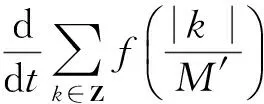
(16)

对式(16)从TK(ω)到t应用Gronwall不等式及应用拉回映射θ-t:ω|→θ-tω,则

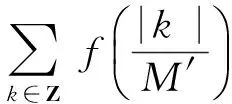
(17)

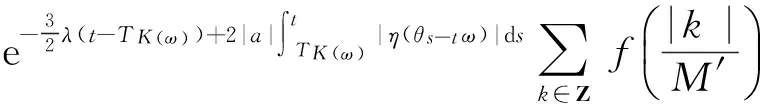
(18)

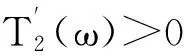
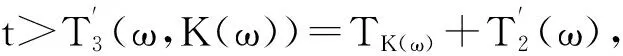
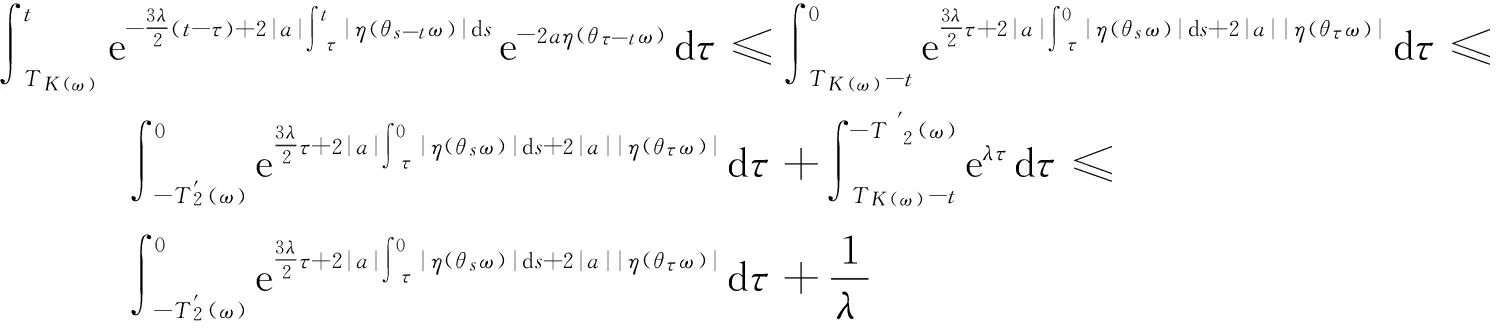
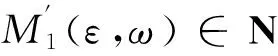
(19)

3)由于R(ω)是缓增随机变量且R(θtω)关于t连续,所以可由文献[12]的命题4.33可得,存在缓增随机变量δ(ω)>0,使得

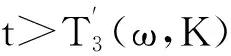
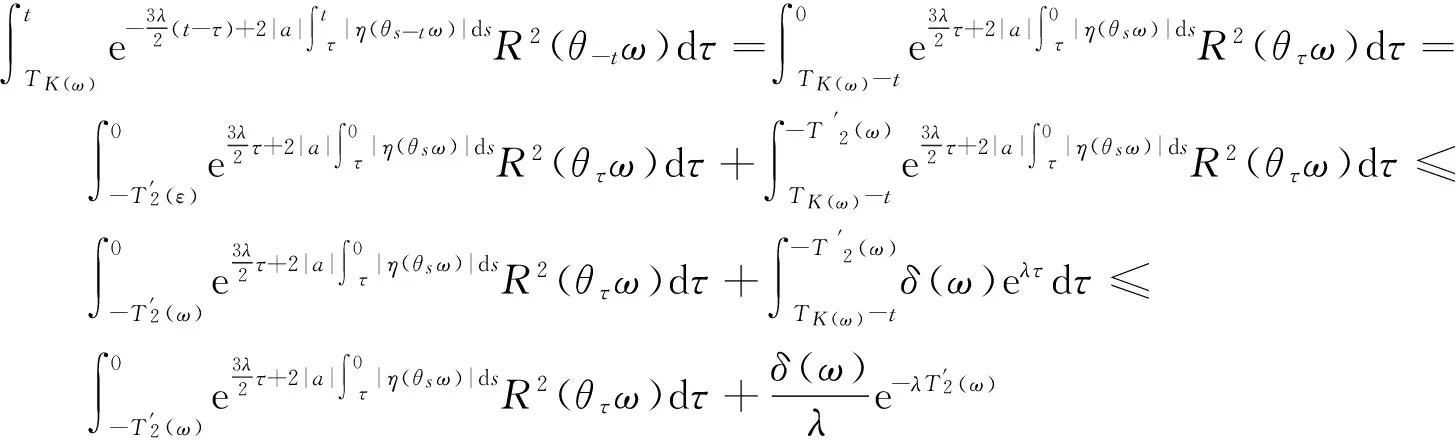
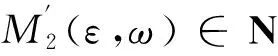
(20)

令

(21)

综合式(17)～式(21)可得:∀ε>0,ω∈Ω,当t>T′(ε,ω,K(ω)),x0∈K(ω)时,有

(22)

结合文献[11]中的定理3.1可知,{x(t,ω)}t≥0,ω∈Ω存在随机吸引子.定理3证毕.

2 系统(2)的随机吸引子

主要讨论系统(2)的随机吸引子的存在性.系统(2)等价于

(23)

令y=ueiaη(θtω),则y,u在l2上同构且‖y‖=‖u‖,系统(23)等价于

(24)

定理4 若假设(A1)和(A2)成立,则

1)对∀ω∈Ω,y0∈l2,系统(24)存在唯一解y(·)=y(·,ω,y0)∈C1((0,+∞)∩C([0,+∞),l2),y(·)关于y0连续,并且解y(t,ω,·)生成一个由(Ω,F,P,(θt)t∈R)驱动取值于l2的连续随机动力系统{y(t,ω)}t≥0,ω∈Ω.

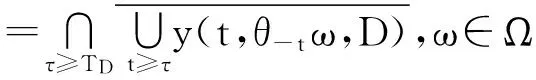
证明 1)证明类似于定理1中的证法,且有

(25)

2)由式(25)得,

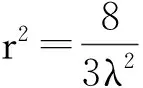
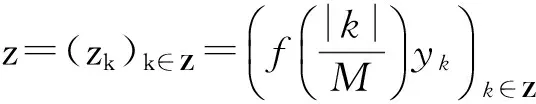
(26)

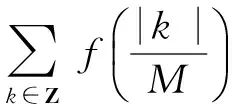
(27)

由于r有界,g∈l2,所以对∀ε>0,ω∈Ω,存在T(ε,D)>TD,M(ε)∈N,使得当t>T(ε,D),M>M(ε)时,有

(28)

从而当t>T(ε,D),y0∈D时,有

(29)

由文献[11]中的定理3.1可知,{y(t,ω,·)}t≥0,ω∈Ω存在随机吸引子.定理4证毕.

注1 系统(1)(或系统(3))与系统(2)(或系统(23))存在随机吸引子的条件是不完全相同的,系统(2)比系统(1)少了一个条件(A3),即限制a的取值.由此可见,系统(2)的随机吸引子的存在性与a的取值无关,而系统(1)存在随机吸引子需要随机项的系数a适当小.

[1]Bates P W,Lisei H,Lu Kening.Attractors for stochastic lattice dynamical systems[J].Stoch Dyn,2006,6(1):1-21.

[2]Bates P W,Lu Kening,Wang Bixiang.Attractors for lattice dynamical systems[J].Internat J Bifur Chaos,2001,11(1):143-154.

[3]Abdallah A Y.Global attractor for the lattice dynamical system of a nonlinear Boussinesq equation[J].Abstr Appl Anal,2005,10(6):655-671.

[4]Abdallah A Y.Long-time behavior for second order lattice dynamical systems[J].Acta Appl Math,2009,106(1):47-59.

[5]Caraballo T,Lu Kening.Attractors for stochastic lattice dynamical systems with a multiplication noise[J].Frontiers of Mathematics in China,2008,6(3):317-335.

[6]Yan Weiping,Li Yong,Ji Shuguan.Random attractors for first order stochastic retarded lattice dynamical systems[J].J Math Phy,2010,51(3):1-17.

[7]Karachalios N I,Yannacopoulos A N.Global existence and compact attractors for the discrete nonlinear Schrödinger equation[J].J Differential Equations,2005,217(1):88-123.

[8]Chen Tao,Zhou Shengfan.Attractors for discrete nonlinear Schrödinger equation with delay[J].Acta Math Appl Sin:English Series,2010,26(4):633-642.

[9]周盛凡,谭慧荣.非线性Schrödinger格点方程的指数吸引子[J].浙江师范大学学报:自然科学版,2015,38(4):361-365.

[10]赵才地,周盛凡.格点系统存在指数吸引子的充分条件及应用[J].数学学报,2010,53(2):233-242.

[11]Han Xiaoying,Shen Wenxian,Zhou Shengfan.Random attractors for stochastic lattice dynamical systems in weighted spaces[J].J Differential Equations,2011,250(3):1235-1266.

[12]Arnold L.Random dynamical systems[M].Heidelberg:Springer-Verlag,1998.

(责任编辑 陶立方)

Random attractor for Schrödinger lattice system with multiplicative white noise

CUI Hongzhen, ZHOU Shengfan

(CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,Jinhua321004,China)

It was mainly studied the existence of a random attractor for stochastic Schrödinger lattice system.Firstly, the stochastic Schrödinger lattice system with multiplicative white noise was transfered into a random dynamical system with random coefficients and without noise by the Ornstein-Uhlenbeck process.Secondly, the existence and uniqueness of solution for lattice system with initial condition were considered, and mapping of this solution generated a random dynamical system. Finally, the problem of the existence of a random bounded absorbing set and a random attractor were also investigated.

random attractor; multiplicative white noise; Schrödinger lattice system; existence

10.16218/j.issn.1001-5051.2017.01.003

2016-03-14；

2016-04-03

国家自然科学基金资助项目(11471290)

崔红珍(1990-),女,山东德州人,硕士研究生.研究方向:动力系统与微分方程.

周盛凡.E-mail: sfzhou@zjnu.cn

O175.25

A

1001-5051(2017)01-0017-07