γ-条件下非精确牛顿类方法的半局部收敛性*

何金苏, 吴阿凡, 沈卫平

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)



γ-条件下非精确牛顿类方法的半局部收敛性*

何金苏, 吴阿凡, 沈卫平

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

研究了非精确牛顿类方法的收敛性问题.假设非线性算子满足γ-条件,那么可以建立非精确牛顿类方法的半局部收敛条件;并且,给出一个数值例子说明了本文结果的有效性.

非精确牛顿类方法;γ-条件;非线性算子;半局部收敛性

0 引 言

设X和Y是Banach空间,Ω是X中的一个开凸集.设非线性算子f:Ω⊆X→Y有连续的F-导数,记为f′.在Banach空间中求解非线性算子方程

(1)

是一个重要的课题,并且在数学理论和应用领域中都有着广泛的应用.其中求解方程(1)的最主要方法就是牛顿法,其迭代形式为

(2)

牛顿法收敛性问题的研究通常分为两类:局部收敛性问题的研究[1-3]和半局部收敛性问题的研究[1-5].研究牛顿法半局部收敛性问题中最著名的理论就是Kantorovich理论[6],它保证了牛顿序列在一个较弱的条件下收敛于方程的解.另一个重要的理论就是Smale的α理论[5],它提出了近似零点的概念,并建立了解析函数判断初始点为近似零点的条件,该理论只依赖于初始点的选择.特别地,文献[2-3]通过利用优序列找到了更好的α判据,改进了Smale的α理论.而且,文献[2]通过引进γ-条件的概念,再次讨论了α判据,推广了Smale的点估计理论.

由式(2)可知,牛顿法要求计算f′(xn),以及精确地求解线性方程

(3)

但是,在实际计算中,牛顿法有时是无效的.因此,学者们提出了牛顿类方法和非精确牛顿法.牛顿类方法能够避免精确计算导数f′(xn);非精确牛顿法采用线性迭代近似求解方程(3)代替精确求解,进而减少牛顿法的计算量.将牛顿类方法和非精确牛顿法结合所得到的方法就是非精确牛顿类方法.通常,非精确牛顿类方法的迭代形式为:

算法1:给定初始点x0,令n=0,1,2,…,执行下列操作,直至{xn}收敛:

1)设rn为残差项,xn为迭代值,求解sn,使其满足Bnsn=-f(xn)+rn;

2)令xn+1=xn+sn;

3)令n=n+1,返回操作1).

其中,{Bn}是一列从X到Y的可逆算子,{rn}是Y中的一个序列(通常依赖于序列{xn}).

当Bn=f′(xn)(n∈N)时,算法1就为非精确牛顿法.众所周知,非精确牛顿类方法的收敛性依赖于残差{rn}.文献[7]通过某种方式分析了局部收敛性,使得相应的残差{rn}满足‖rn‖/‖f(xn)‖≤ηn.文献[8]考虑了相应的残差控制

(4)

并得到了非精确牛顿类方法的局部收敛性结果.其中,{θn}为强制项.

受文献[9-10]中非精确牛顿类方法求解逆特征值问题的启发,文献[11]考虑残差{rn}满足

(5)

式(5)中,0≤β≤1.按照文献[12]中的残差条件的选取,可取式(5)中的β=1,即有

(6)

近几年,对非精确牛顿法或修正的非精确牛顿类方法收敛性的研究较多[13-14].本文对非精确牛顿类方法的收敛性质展开研究,利用满足式(6)的残差控制{rn},研究了在γ-条件下非精确牛顿类方法的收敛性,得到了非精确牛顿类方法的半局部收敛性定理;同时,给出了一个数值例子,说明本文结果的有效性.

1 预备知识

(7)

设{tn}是由牛顿类方法生成的序列,且其初始点为t0=0,定义

(8)

根据文献[15]中的引理2.2可以描述序列{tn}的收敛性质.

引理2 假设式(7)成立.设t*是方程φ(t)=0的较小的非负解，则由式(8)生成的序列{tn}单调递增并收敛于t*，同时tn+1-tn≤b,tn<2b,n∈N.

2 收敛性分析

设f:Ω⊆X→Y是具有一阶连续和二阶连续F-导数的算子,分别记为f′和f".并设x0∈Ω,且f′(x0)-1存在.

首先,给出γ-条件的定义及相关的引理.

(9)

则称函数f在x0处满足γ-条件.

(10)

其中,τ1,τ2是某些非负常数.

为了得到主要依赖于初始点x0的收敛条件,取

(11)

设ω1≥1,ω2≥0,并假设序列{Bn}满足:

(C2)‖f′(x0)-1(Bn-f′(xn))‖≤ω2‖f′(x0)-1f(xn)‖,n∈N.

设

(12)

(13)

并且,{tn}是由式(8)生成的序列.

下面给出本文的主要结果.

定理1 设f满足γ-条件(9),取r=t*,并设

(14)

则由算法1生成的序列{xn}是有定义的,且收敛于f(x)=0的解x*,满足

(15)

(16)

为完成证明,需证明

(17)

(18)

下面用数学归纳法证明.当n=0时,由α与b的定义可知

所以,当n=0时,式(17)成立.

由残差公式(6)和式(11)可知

v‖f′(x0)-1f(xn)‖2.

(19)

因此,由条件(C1)、式(12)和式(19)有

ω1(α+v‖f′(x0)-1f(x0)‖2)=ω1(α+vα2).

从而,当n=0时,式(18)也成立.

‖f′(x0)-1(f′(xm-1)-Bm-1)(xm-xm-1)‖+‖f′(x0)-1rm-1‖.

(20)

下面证明

(21)

(22)

(23)

由式(18)(n=m-1)可得,

(24)

特别地,

所以,

(25)

且

因此,引理3成立.由式(9)和式(24)有

(26)

(27)

从而,式(26)变为

最后一个不等式由式(16)和式(25)可得.因此,式(21)成立.又由条件(C2)可知

‖f ′(x0)-1(Bm-1-f ′(xm-1))(xm-xm-1)‖≤

‖f ′(x0)-1(Bm-1-f ′(xm-1))‖5‖xm-xm-1‖≤

ω2‖f ′(x0)-1f(xm-1)‖5‖xm-xm-1‖.

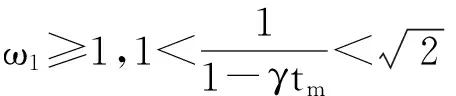
再由式(18)(n=m-1)可得

‖f′(x0)-1(Bm-1-f′(xm-1))(xm-xm-1)‖≤

ω2‖f′(x0)-1f(xm-1)‖5‖xm-xm-1‖≤ω2(tm-tm-1)2.

另外,由式(19)和式(20)可得

因此,式(22)和式(23)均成立.将式(21)、式(22)和式(23)合并可得

且φ′(tm)=atm-1,所以

(28)

从而,当n=m时,式(17)成立.又由条件(C1)和式(19)有

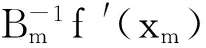
ω1‖f′(xm)-1f′(x0)‖(‖f′(x0)-1f(xm)‖+v‖f′(x0)-1f(xm)‖2).

从而,

因此,由引理3和式(28)可得

从而,当n=m时,式(18)成立.综上,定理1得证.

当Bn=f′(xn)(n∈N)时,条件(C1)和(C2)满足ω1=1,ω2=0.因此,

那么,非精确牛顿法的收敛结果就可直接从定理1得到.从而有如下推论:

推论1 设f满足γ-条件(9),取r=t*,并设

则由非精确牛顿法生成的序列{xn}是有定义的且收敛于f(x)=0的解x*,并满足

3 数值例子

本文将引用文献[12]中的例子说明定理1的有效性.为了方便,取ω1=1,ω2=0,则

并且,选取Pn=I,n∈N.

例1 设X=Y=R2,并分别将X和Y赋予l1-范数和l∞-范数.定义解析函数f:X→Y为

设x0=(u,w)T∈X,则

(29)

式(29)中,

因此,

从而,

首先,通过取4个不同的初始点x0=(0.002,0.002)T,(0.002,-0.002)T,(0.01,0.035)T,(0.05,0.05)T估计γ和α的值,结果见表1.为了说明本文结果的有效性,考虑θn的不同取值,并用“T”和“F”表示式(15)的成立与失败,结果见表2.

表1 γ值和α值的估计

表2 不同θn值对式(15)的T/F值

从表2可以看出,即使是同一初始点x0,在不同的θn值下也有不同的T/F值;同样地,在同一θn值下,取不同的初始点x0,也得到不同的T/F值.

[1]Wang Xinghua.Convergence of Newton′s method and inverse function theorem in Banach space[J].Math Comp,1999,68(225):169-186.

[2]Wang Xinghua,Han Danfu.On the dominating sequencee method in the point estimates and Smale′s theorem[J].Sci China Ser A,1990,19(9):135-144.

[3]Wang Xinghua,Han Danfu.Criterionαand Newton′s method[J].Chinese Numer Math Appl,1997,19(2):96-105.

[4]Smale S.Complexity theory and numerical analysis[J].Acta Numer,1997,6(1):523-551.

[5]Smale S.Newton′s theory estimates from data at one point[M].New York:Spring-Verlag,1986.

[6]Kantorovich L V.On Newton′s method for functional equations[J].Dokl Akad Nauk,1948,59(7):1237-1240.

[7]Dembo R S,Eisenstant S C,Steihaug T.Inexact Newton methods[J].SIAM Numer Math,1982,19(2):400-408.

[8]Morini B.Convergence behaviour of inexact Newton methods[J].Math Comp,1999,68(228):1605-1613.

[9]Chan R H,Xue S F,Zhou H M.On the convergence rate of a quasi-Newton method for inverse eigenvalue problems[J].SIAM Numer Anal,1999,36(2):436-441.

[10]Chan R H,Chung H L,Xue S F.The inexact Newton-like method for inverse eigenvalue problem[J].BIT Numer Math,2003,43(1):7-20.

[11]Li Chong,Shen Weiping.Local convergence of inexact methods under the Hölder condition[J].Comp Appl Math,2008,222(2):544-560.

[12]Shen Weiping,Li Chong.Smale′sαtheory for inexact Newton methods under theγ-condition[J].Math Anal Appl,2010,369(1):29-42.

[13]Argyros I K,Khattri S K.Weaker Kantorovich type criteria for inexact Newton methods[J].Comp Appl Math,2014,261(261):103-117.

[15]Shen Weiping,Li Chong.Convergence criterion of inexact methods for operators with Hölder continuous derivatives[J].Taiwanese Math,2008,12(7):1865-1882.

(责任编辑 陶立方)

The semi-local convergence for inexact Newton-like methods under theγ-condition

HE Jinsu, WU Afan, SHEN Weiping

(CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,Jinhua321004,China)

It was studied the convergence problem of inexact Newton-like methods. Under theγ-condition, a semi-local convergence criterion for inexact Newton-like methods was established; furthermore, a numerical example was presented to illustrate the effectiveness of the results.

inexact Newton-like methods;γ-condition; nonlinear operator; semi-local convergence

10.16218/j.issn.1001-5051.2017.01.002

2016-04-27；

2016-06-11

国家自然科学基金资助项目(11571308)

何金苏(1965-),女,浙江金华人,教授.研究方向:数值逼近.

O241.5

A

1001-5051(2017)01-0009-08